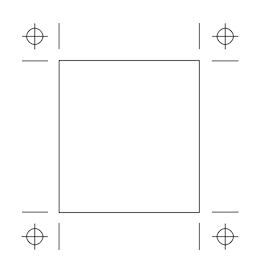
I’ve been interested in these "box corner" patterns for a while:
Out of curiosity, I did a brute force search for other pairs of similar patterns, where the center symbol is the same, and the north/south and east/west "edges" of the corresponding box corners match. Here’s one pattern I found:
I found another pair, but they intersect in an interesting way:
The 408 only has one pair of similar patterns in a "box corner" arrangement:
What relationship does 340’s encoding scheme have with the appearance of these patterns? Or are they just appearing by chance? Or do I need to get out more?
It’s finally happened dave. Patterns. When all else is lost all we are left with is …patterns. I was doing it too last night. You may recall my own min-breakdowns such as "Diagonals" and "Separated by one line, two lines, three lines" etc, etc. 
“I don’t know Chief, he’s very smart or very dumb.“
They always looked like crop marks to me:
The registration marks above should also look familiar 
So, who knows, maybe a way to split the cipher in custom segments. I have worked with this idea in the past unsuccessfully.
For the 2nd image at the top I find it interesting that these patterns all start at uneven rows, if grouping the cipher in pairs of rows they would remain intact. There may be a different path going on for the 340, either done before or during the encoding process. If done during, then it should be reasonably subtle (mot too much vertical transposition) because the cycles are still somewhat intact.
I’ve done not much work on these, just some basic stuff by hand with my pathing tool in Examine some while ago.
Example:
Grouping of symbols "+" and "R" is also interesting.
Interesting ideas, Jarlve. Have you already unfolded those paths and fed the resulting transformed 340 into your solver?
The frequent contact of ‘R’ with ‘+’ is interesting, so I ran a quick test to dump all such adjacencies.
For each ‘+’, this is count how many times other symbols appear right next to it (in any direction: N S E W NE NW SW or SE):
+ (16), R (11), 2 (8), c (7), ^ (7), O (7), F (7), z (6), # (5), | (4), b (4), V (4), U (4), M (4), J (4), 8 (4), 5 (4), – (4), & (4), p (3), l (3), f (3), T (3), P (3), L (3), ; (3), . (3), ) (3), y (2), t (2), k (2), Z (2), G (2), E (2), C (2), > (2), < (2), ( (2), j (1), _ (1), Y (1), W (1), S (1), N (1), K (1), D (1), B (1), A (1), @ (1), : (1), 7 (1), 6 (1), 4 (1), 3 (1), * (1)
Now, it’s very interesting to me that the ‘B’ symbol, which is the 2nd most frequent symbol in the cipher (appearing 12 times), manages to avoid direct contact with ‘+’ all but 1 time.
So it appears the ‘+’ is prime-phobic as well as ‘B’ phobic. 
I wonder if this is a real phenomenon (a symptom of the encoding method) or yet another red herring. Should be easy to estimate the probability by shuffling the 340 randomly and counting how many times ‘B’ touches ‘+’.
Interesting ideas, Jarlve. Have you already unfolded those paths and fed the resulting transformed 340 into your solver?
Yes, but there is lots more that can be done in this direction.
I wonder if we can quantify how much sets of symbols (to some depth) like to group together grid wise and compare that to the 408 and other ciphers.
A clustering measurement would be interesting to explore.
One way might be to consider a small rectangular window (3×3 or 5×5). For each window in the 340, track the symbols that appear in it. Then for each distinct combination of 2, 3, 4, or 5 symbols from the ciphers alphabet, count how many windows in which all those symbols appear. Normalize the score based on the constituent symbols’ frequencies.
If, say, some combination of 4 symbols appears in many windows, then you could conclude that those 4 symbols seem to cluster well together.
Another way could be to compute Euclidian distance between every combination of 2 symbols. Then for each combination of closely related symbols, find a 3rd symbol that is frequently close to either of the 2 symbols. Continue in this way to form groups of symbols that cluster well together.
A clustering measurement would be interesting to explore.
One way might be to consider a small rectangular window (3×3 or 5×5). For each window in the 340, track the symbols that appear in it. Then for each distinct combination of 2, 3, 4, or 5 symbols from the ciphers alphabet, count how many windows in which all those symbols appear. Normalize the score based on the constituent symbols’ frequencies.
If, say, some combination of 4 symbols appears in many windows, then you could conclude that those 4 symbols seem to cluster well together.
Another way could be to compute Euclidian distance between every combination of 2 symbols. Then for each combination of closely related symbols, find a 3rd symbol that is frequently close to either of the 2 symbols. Continue in this way to form groups of symbols that cluster well together.
Good ideas, thanks. I have something in place a bit similar, I can specify any box dimensions 2×3, 3×3, 5×10 and look for repeating patterns. When comparing these scores to other orientations for various box dimensions the regular horizontal 340 scores higher. Though the horizontal favor is much more pronounced in the 408. But with the "+" symbol in the 340 it’s so hard to take anything for granted.
One observation that explains the grouping of symbols is this. On the left image I selected all the symbols that represent the letter "l" in the 408, a letter that likes to stick to itself. On the right image I added the letter "i", which in turn likes to stick with the letter "l" and so islands begin to appear. Gaps between letters "i" and "l" can be filled up with letters that like to stick between these letters and so forth. Perhaps just the same is going on with the 340 and can be used to our advantage (somehow).
