Using the last experiment where 63, 64 and 65 were expanded, I merged the cycles with 2 to 4 symbols in them to see what would happen. I got the symbol count and multiplicity down to 87 and 0.256 for a fairly readable solution with score 43403:

25 30 25 29 101 29 25 30 30 25 35 20 44 13 39 44 30
14 102 121 151 1 58 49 16 25 53 25 49 49 40 33 58 7
152 19 58 35 25 122 25 49 33 41 45 17 19 58 35 55 21
2 103 104 25 30 30 25 35 20 60 105 30 123 124 3 33 18
25 35 56 125 12 19 42 45 45 13 49 57 126 14 7 4 58
106 15 33 5 35 25 49 53 21 16 33 43 49 54 9 1 35
20 17 127 39 58 49 2 35 25 33 3 30 40 19 4 30 30
55 41 29 25 30 30 49 42 128 18 56 21 25 129 20 20 25
59 12 49 130 13 131 21 14 33 43 153 53 54 21 45 25 30
30 25 35 20 15 132 44 16 133 17 107 7 18 25 154 12 59
13 134 6 14 55 56 15 45 57 21 155 108 20 16 53 54 25
35 20 62 39 58 45 45 40 7 29 49 41 19 135 60 156 55
21 1 20 25 45 30 136 21 17 6 18 157 57 44 2 45 53
42 19 25 54 25 49 55 21 3 56 60 21 12 35 25 137 138
30 158 6 13 45 14 6 43 45 35 25 35 44 4 45 5 139
25 7 15 1 35 159 2 30 30 109 21 16 25 21 3 59 17
29 25 30 140 18 9 60 25 30 141 6 12 7 160 33 13 33
142 143 30 4 59 14 49 25 60 25 30 30 35 40 53 20 110
59 15 62 41 58 33 62 35 161 33 16 6 162 7 1 58 49
18 62 42 58 60 111 30 30 54 45 62 55 43 49 30 39 144

I L I K E K I L L I N G P E O P L
E A S P A U S E I T I S S O M U C
H F U N I T I S M O R E F U N T H
A D W I L L I N G T O L E C A M E
I N T H E F O R R E S T H E C A U
S E M I N I S T H E M O S T R A N
G E R O U S A N I M A L O F A L L
T O K I L L S O M E T H I N G G I
V E S H E D H E M O U T T H R I L
L I N G E S P E R E N C E I N E V
E R B E T T E R T H I N G E T T I
N G Y O U R R O C K S O F I T I T
H A G I R L S H E B E S T P A R T
O F I T I S T H A T T H E N I N G
L Y B E R E B O R N I N P A R I F
I C E A N D A L L T H E I H A V E
K I L L E R T I L L B E C O M E M
E D L A V E S I T I L L N O T G I
V E Y O U M Y N A M E B E C A U S
E Y O U T A L L T R Y T O S L O W

So it could work. A combination of incremental expanding of wildcards and merging of cycles maybe could be used to find a solution…

Smokie

Hey smokie,

Your wildcard hypothesis is still on my mind also. Because, it may be a bit strange for a 63 symbol cipher to have possibly 4+ 1:1 substitutes. Ofcourse there are other alternatives. It’s DARPA hard.

Jarlve,

It is hard, and probably beyond my abilities to do anything about it. But Quicktrader was right. The cycles are there and that’s the best approach.

Let me ask you, don’t the cycles prove that the message is left right top down? Or asked another way, is there any way to construct a ciphered message that isn’t left right top down, but results in cycles with the same statistics?

I think that you were on the right track with the transposition idea also. Few of the cycles are perfect throughout.

Regarding your last comment about 4+ 1:1. See Quicktrader’s first post.

In the 408, Zodiac used high count 1:1 for letters B, C, G, M, W and Y. And there is 1:1 for P and V also.

My last set of experiments show that ZKD1.2 can find a somewhat readable solution with two polyalphabetic symbols with total count 35. Add one more polyalphabetic symbol with count of 10, and you have an unsolvable message.

Smokie

Let me ask you, don’t the cycles prove that the message is left right top down? Or asked another way, is there any way to construct a ciphered message that isn’t left right top down, but results in cycles with the same statistics?

I think all you would have to do is rewrite the plaintext in the different direction (let’s say down-top-right-left), and then assign the symbols by reading the result in the normal order (left-right-top-down) and cycling through the symbols for high-frequency letters.

O.k., I see that. He could have written the message in any direction and assigned cycle symbols left to right, top to bottom. So I guess that’s where we are. Wildcards or a different message route.

EDIT: Is there any other way to get the same cycle score distribution that you made?

Let me ask you, don’t the cycles prove that the message is left right top down?

I think it is pretty certain at this point that Z340 should be read horizontally (i.e. by rows, not columns). Simple repeat counts in rows vs columns show that. Even if you format Z340 as 20 symbols in 17 rows (vs the default 17 symbols in 20 rows), the repeat counts in columns are higher than in rows, even though columns are now shorter than rows. Regarding left to right vs right to left – that’s easy. All you have to do is try each way and see which works. Counting reversing the whole message, or only the rows, or only every other row (odd or even, i.e. snake patter starting from top left, top right, bottom left, bottom right), you end up with just 1 + 1 + 4 possibilities, or 6 total. It shouldn’t be too hard to try every way to see if anything pans out.

Ah, that’s true, I had forgotten that the symbol assignments would not hide all the repeats.

Talking about direction of encoding or plaintext?

Plaintext.

Not sure if I’m missing something but for the 340 the lower repeat counts for the rows are due to the (cyclic) encoding in that direction.

Jarlve: Remember when you made ciphered messages for me with almost perfect cycles but then I found other false cycles to support my Wildcard Hypothesis? I have been thinking for the last couple of days about what you just said today.

If you make a message with cycles, they will overlap each other. The overlapping will create false cycles, which will disappear more and more the farther you get into the message. Cycles that maintain throughout are probably man made, and cycles that fizzle out after two or three repetitions and halfway through the message are probably false.

So, my question is, did Zodiac realize about the overlapping and abandon the cycling at the end of the message to camouflage the real cycles among the false cycles (there are only a few that maintain throughout in the 340)? Did Zodiac abandon the cycling near the end for some other reason? Laziness? To be funny? Maybe Zodiac at some level had some thought in his head about the overlapping and false cycles…

Doranchak: Did you lose interest in the hillclimber for the + that you were working on? If it didn’t work, I understand.

General: In any case, I have been working on the Z340 some more. I have been working on my scoring, taking big cues from doranchak. I have been thinking about ways to find the cycles outside of what doranchak has already provided because so many of them must be false.

Imagine the symbols arranged in a big circle 1-63 , with the two-symbol scores between each pair of symbols. Make random mutations by switching two symbols, and total up the score. If the total score is higher than the original total score, then keep the mutations and mutate again. Eventually the symbols in a cycle will all coalesce to each other; the cycle symbols will aggregate to each other. I have a new spreadsheet that does this and it works pretty well (but not perfect) on a test message. It excludes a lot of the false cycles with what I think you guys call a global optimum. It’s not a circle, though. It’s a horizontal string with mathematically connecting ends.

This work in progress is Experiment 2, with perfect cycles:

See: viewtopic.php?f=81&t=267&start=50, post # 7, p70chs63.txt (this is Experiment 2 J-ST, or "Experiment 2").

Smokie

So, my question is, did Zodiac realize about the overlapping and abandon the cycling at the end of the message to camouflage the real cycles among the false cycles (there are only a few that maintain throughout in the 340)? Did Zodiac abandon the cycling near the end for some other reason? Laziness? To be funny? Maybe Zodiac at some level had some thought in his head about the overlapping and false cycles…

I’m inclined to say no because if he wanted to hide the cycles he could just have used no cycles at all.

Before you started your work on the cycles I was working with my measurement of the non-repeats (summed frequencies of strings which have no repeat), which gives a good approximation to how cyclic a cipher is. I noticed it was kinda low for the 340, furthermore it had a strange peak at 17, which is high. There are 26 distinct strings of 17 symbols in the 340 that have no repeats. So I wrote a small program to look for interruptions, there is an image in this thread which shows this, basicly your 4 wildcard candidates show up as the main interruptors. And when I compile such an image for the 408, not much interruptions show up at all. There is definitely something going on.

When I remove these 4 symbols from the 340 and compare what is left versus the 408 the 340 actually seems to be more cyclic (by non-repeats) than the 408. What do you think? As we have discussed before this doesn’t mean that they are wildcards, as they could also be 1:1 substitutes. I don’t favor either wildcards, 1:1 substitutes or anything else for that matter. I think it’s also possible that up to a certain number of symbols (maybe 10+) are actually nulls, and that whatever is supposed to remain cycles perfectly. That’s another theory, and maybe less plausible since bigram repeats don’t improve for the horizontal direction after removing your 4 wildcards.

You should read Nick Pellings idea’s for the 340 in this article: http://www.ciphermysteries.com/2015/06/ … ng-opinion

As doranchak pointed out in the comments, it somewhat overlaps with some of the work in this thread. He’s also hinting at a 2-part cipher, that the top 10 rows versus bottom 10 rows have a different encoding, but with the same symbols. I’d like you to take a look at that (if you want ofcourse), and see if you can support that theory or not. Myself I don’t believe it’s actual, at least not in this straightforward manner. But I continue to monitor for it with my solver.

I really like your hill climber!

I’m inclined to say no because if he wanted to hide the cycles he could just have used no cycles at all.

I agree.

Before you started your work on the cycles I was working with my measurement of the non-repeats (summed frequencies of strings which have no repeat), which gives a good approximation to how cyclic a cipher is. I noticed it was kinda low for the 340, furthermore it had a strange peak at 17, which is high. There are 26 distinct strings of 17 symbols in the 340 that have no repeats. So I wrote a small program to look for interruptions, there is an image in this thread which shows this, basicly your 4 wildcard candidates show up as the main interruptors. And when I compile such an image for the 408, not much interruptions show up at all. There is definitely something going on.

When I remove these 4 symbols from the 340 and compare what is left versus the 408 the 340 actually seems to be more cyclic (by non-repeats) than the 408. What do you think?

I don’t know. A couple of years ago I made a spreadsheet to count when symbols were repeated because I wanted to know if the upper half, lower half theory is supported by finding few repeated symbols in lines 1-3 and 10-13. It doesn’t matter where in the message you start counting repeats. Basically you will get a flat line that starts curving upward at about 17. Very low slope at first, but you’re going to get a 45 degree line eventually.

As we have discussed before this doesn’t mean that they are wildcards, as they could also be 1:1 substitutes. I don’t favor either wildcards, 1:1 substitutes or anything else for that matter. I think it’s also possible that up to a certain number of symbols (maybe 10+) are actually nulls, and that whatever is supposed to remain cycles perfectly.

I am beginning to agree with you. Before I was arguing that 5, 20 and 51 are wildcards because they are high in count and don’t cycle well with other symbols. But if there are wildcards, they could very well be low in count. Meaning that there could be a lot of symbols that are each low in count, and used as wildcards. Or like you say, they could be something else. I like the 10+ symbol null idea. I’m not married to anything either (today).

You should read Nick Pellings idea’s for the 340 in this article: http://www.ciphermysteries.com/2015/06/ … ng-opinion

I did and it was good. Why didn’t he test his theory about the + meaning to double the prior symbol? Maybe he did but there is more going on.

He’s also hinting at a 2-part cipher, that the top 10 rows versus bottom 10 rows have a different encoding, but with the same symbols. I’d like you to take a look at that (if you want ofcourse), and see if you can support that theory or not.

And I will. I am convinced that further study of the cycles is the key to this. Different ways to score them and different ways to look at them. Where in the message they appear. Two symbols of different count with high scores. There is a lot of this stuff: A B A B A B A B A B A A A A. Not much of this stuff: A A A A A B A B A B A B A B. Etc.

Think about this question. Do cycle symbols appear only in certain columns? Are there some columns that don’t have cycle symbols? Just identifying a handful of the most likely cycles could be the key because then we could look at where those symbols are and where they are not. Are they distributed evenly throughout?

Thanks for the compliment on my very first hillclimber. It’s still a work in progress, but I want it to gather together cycle symbols even if there is some randomization in the symbol selection. I did use it on the Z340, but am still a bit uncertain about my scoring. I have to go back and look for doranchak’s formulas. Right now A B A B A B = 2^6 = 64. But what if I have A B A B A B B A A A A B ? Right now I have (2^6) + (2^2) = 68. But I don’t think that is right either.

I’ll share a little bit about the 340 cycling. Just a bit more information. I took all of the two-symbol cycles and scored them just by their maximum probability. In the above example, A B A B A B B A A A A B would merely score 64. So would any cycle with six alternations, no matter where they are.

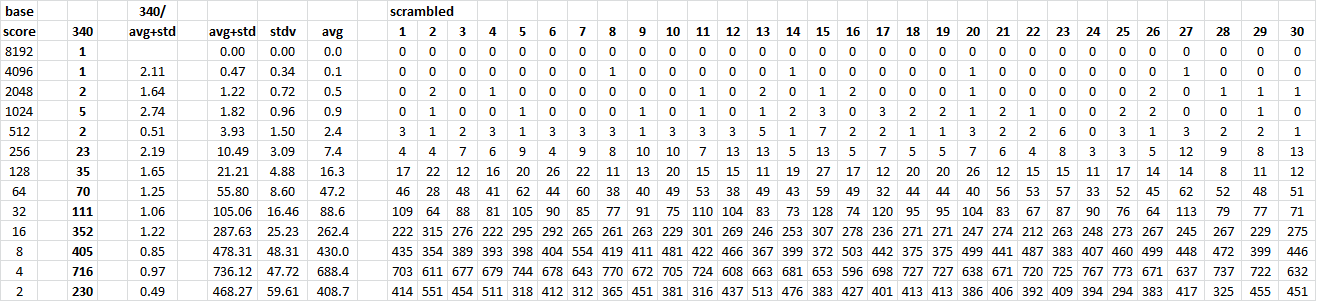
For example, Z340 has 23 total two symbol cycles with eight alternations for 2^8=256. I scrambled the message 30 times and in those 30 scrambled messages, there was a mean number of 7.4 cycles with score of 256. The standard deviation was 3.09 and mean + standard deviation 10.49. In other words, of those 23 cycles with score of 256, about 12 of them are likely Zodiac made, and 11 of them are random.

Anyway, I have to go back and do some research on the scoring. I can make quick easy adjustments to my spreadsheet and examine parts of the message for cycles, and will get to the first half – second half analysis. That’s high on my list.

Smokie

You should read Nick Pellings idea’s for the 340 in this article: http://www.ciphermysteries.com/2015/06/ … ng-opinion

I did and it was good. Why didn’t he test his theory about the + meaning to double the prior symbol? Maybe he did but there is more going on.

I’m sure he did, and found out that it didn’t lead to a solve. 🙂 But he probably decided to mention it anyway because he didn’t want to discourage anyone from trying it too, since you still need to solve the substitutions after decoding whatever ‘+’ does, and there is no general solution to that encryption method. I’ve actually had the same idea (that ‘+’ symbol is a meta-symbol) and tried a few possibilities. I obviously didn’t get a solve, but I was only using the current version of ZKD, and haven’t tried it with the new improved version of AZD yet. Here’s what I tried for a ‘function’ of the ‘+’ symbol: double previous symbol, double next symbol, remove previous symbol, remove next symbol, double previous digraph (i.e. two previous symbols), double next digraph. I haven’t tried removing digraphs, because it would reduce the length of the cipher to only 268 symbols, and it’s way too low to get a solve (i.e. multiplicity is too high). I encourage you to try my ideas with your favorite auto-solver to see if you get somewhere. I would also love to get more ideas as to what the ‘function’ of the plus symbol might be?

I’ve also thought that ‘+’ might stand for more than one letter in the plaintext, such as "the" or "and" (the top two 3-grams, the 3rd one: "ing"). It even occurred to me that Zodiac *always* used ampersand instead of "and" in his letters, which he wrote practically the same as a ‘+’ sign. However, as you all know, ‘+’ doubles up ("++") in Z340 in 3 separate places. It is already quite unlikely to get THETHE or ANDAND in an English text, but 3 times within 340 characters? I’ve actually checked my 6-gram frequencies from a corpus of about 1Gb of English text (no spaces), and here’s the data:
THETHE: 16,158 out of 938,985,052, or 0.0017%
ANDAND: 34,790 out of 938,985,052, or 0.0037%
INGING: 27,142 out of 938,985,052, or 0.0029%
So you need a text of roughly 27,000 letters to get the most frequent ANDAND by chance (938,985,052/34,790), and even longer for THETHE or INGING. And that’s just once. Seems very improbable for Z340.

Maybe ‘+’ stands for a digraph, or 2 letters? Let’s check the numbers. The most frequent digraph in English is TH. According to the data from Practical Cryptography website, it has the frequency of 2.7% in an average English text. So it should be expected to appear just 9 times (339 * 2.7 / 100) in a text of 340 letters (or 339 digraphs). ‘+’ appears 2.7 times more often in Z340. Seems unlikely to me?

I just tried adding an extra new symbol next to ‘+’ to turn it into a digraph, so that ZKD/AZD will automatically try various possibilities and… didn’t get a solve. I did several restarts after a few minutes of running ZKD, and interestingly enough (or perhaps unsurprisingly?), pretty much every time ZKD ended up with TH for my new [+~] digraph. Just for yucks, I tried the same trick with 3 symbols for each ‘+’ (I used [+~=]), and didn’t get anything readable. Again, and this time unsurprisingly, the most frequent trigraphs I got were ING and AND.

P.S. I actually nearly fell of my chair when I spotted …HISLORDTHINGTHEEFORMPEOPLETODAY… in one of the solves, but the rest was pure unadulterated gibberish. 🙂

Anyway, I spent the day working on different scoring systems for my cycle "hillclimber," if that’s what it is.

This is the best I have so far for Experiment 2, which has perfect cycles. The spreadsheet gathers together most of the cycle symbols. I need to do some fine tuning.

See: viewtopic.php?f=81&t=267&start=50, post # 7, p70chs63.txt (this is Experiment 2 J-ST, or "Experiment 2").

The plaintext I know from the answer. I marked where the spreadsheet gathers together symbols that score low, but represent the same letter. For instance, symbols 42 and 47 map to V. The score is only 8 because of the low count. But yet, the spreadsheet pushes them together. Similarly with plaintext G and D. So it seems that the spreadsheet gathers together higher scoring relationships, and pushes together lower scoring relationships.

It doesn’t work perfectly. The symbols for M, 4, 53 and 56, didn’t gather together. And the symbols for S didn’t all gather together either. I’m going to fine tune my scoring a little bit, and I need to try different messages with perfect cycling and with some randomization. Then to the 340. It’s just some fun for me, and I don’t know what will come of it. The 340 is such a mess that this may not be much help. But maybe taking out some of the symbols or making adjustments will. That’s it for a while.

If anybody wants to mess around with this concept, you are welcome to. If not, that’s fine as well. I’ll just keep chipping away when I can.