And I will. I am convinced that further study of the cycles is the key to this. Different ways to score them and different ways to look at them. Where in the message they appear. Two symbols of different count with high scores. There is a lot of this stuff: A B A B A B A B A B A A A A. Not much of this stuff: A A A A A B A B A B A B A B. Etc.

That reminds me of the 408.

Think about this question. Do cycle symbols appear only in certain columns? Are there some columns that don’t have cycle symbols? Just identifying a handful of the most likely cycles could be the key because then we could look at where those symbols are and where they are not. Are they distributed evenly throughout?

Good question, you could possibly do this by adding the total score of each cycle to their spots in a 17 by 20 grid and then total the columns, rows (and possibly normalize these by dividing the column and row totals by the number of elements in the column, row).

I’m sure he did, and found out that it didn’t lead to a solve. But he probably decided to mention it anyway because he didn’t want to discourage anyone from trying it too, since you still need to solve the substitutions after decoding whatever ‘+’ does, and there is no general solution to that encryption method. I’ve actually had the same idea (that ‘+’ symbol is a meta-symbol) and tried a few possibilities. I obviously didn’t get a solve, but I was only using the current version of ZKD, and haven’t tried it with the new improved version of AZD yet. Here’s what I tried for a ‘function’ of the ‘+’ symbol: double previous symbol, double next symbol, remove previous symbol, remove next symbol, double previous digraph (i.e. two previous symbols), double next digraph. I haven’t tried removing digraphs, because it would reduce the length of the cipher to only 268 symbols, and it’s way too low to get a solve (i.e. multiplicity is too high). I encourage you to try my ideas with your favorite auto-solver to see if you get somewhere. I would also love to get more ideas as to what the ‘function’ of the plus symbol might be?

I want to note that my solver seems to be really good at solving ciphers for which the ‘high multiplicity component" is mainly brought on by the number of characters. I just tested that it should be no problem to remove a third of the characters for a 63 symbol cipher. I recommend queuing at least 100 cipher copies at 3.000.000 keys per cipher and checking the top results. To quote from the My work thread:

The program has lost about half of it’s speed but it’s a much more powerful solver now. There seem to be some things that it excels at, for instance, reasonable short strings of ciphertext with not too many symbols. An example of this is given by a solve of the first 8 rows of the 408 (multiplicity 0.375). Which was achieved by changing the Ioc target weight to 2 and many attempts. It now supports up to 200 unique symbols and ciphertexts up to 10.000 characters.

ilikekillingpeopl
ebecauseitissomuc
hfunitismorefurth
ankillingwillgame
intheforcestbecau
semaristhemoathan
gertueanamalofall
tokillsomethinggi

And here’s a solve for a 87 character, simple substitution cipher, to show that it could crack the dorabella.

ilikekillingpeoplebecauseitis
somuchfunitisevenmorefunthank
illingwillgameintheforestbeca

OROQKQORROTMVKUVRKHKIGAYKOZOY
YUSAINLATOZOYKBKTSUXKLATZNGTQ
ORROTMCORJMGSKOTZNKLUXKYZHKIG

It doesn’t work perfectly. The symbols for M, 4, 53 and 56, didn’t gather together. And the symbols for S didn’t all gather together either. I’m going to fine tune my scoring a little bit, and I need to try different messages with perfect cycling and with some randomization. Then to the 340. It’s just some fun for me, and I don’t know what will come of it. The 340 is such a mess that this may not be much help. But maybe taking out some of the symbols or making adjustments will. That’s it for a while.

I can see that it does indeed push cycles together, it’s a great start! Are you using steepest ascend hill climbing?

I can see that it does indeed push cycles together, it’s a great start! Are you using steepest ascend hill climbing?

I don’t know what that is. I have a spreadsheet with 4,000 rows. Each row switches two symbols, and then the total score between the adjacent symbols is compared to the total score between the adjacent symbols on the prior row. If the new score is higher, then I keep the "mutation" and switch another two symbols. I keep track of highest scores, and cut and paste the new sequences into the top row (because 4000 rows is about all the spreadsheet can handle). After maybe 16,000 mutations or so, I have a score that I can no longer make higher.

You can see with the above example, in Experiment 2 the V is 42 and 47. The cycles were only 42 47 42 47. Yet the spreadsheet put those together despite all of the random short cycles that look just like that. It was the message about the Shaman.

For some reason the spreadsheet works really well to gather together cycles with only three symbols, but I am not sure why.

The goal is to eventually make a short list of symbol pairs that can be merged together in the 340. About 126 [ EDIT 63 ] symbol pairs, of which only some percentage truly represent the same letter.

I applied Experiment 3 to my cycle "hillclimber" spreadsheet. Jarlve had randomized several of the cycles:

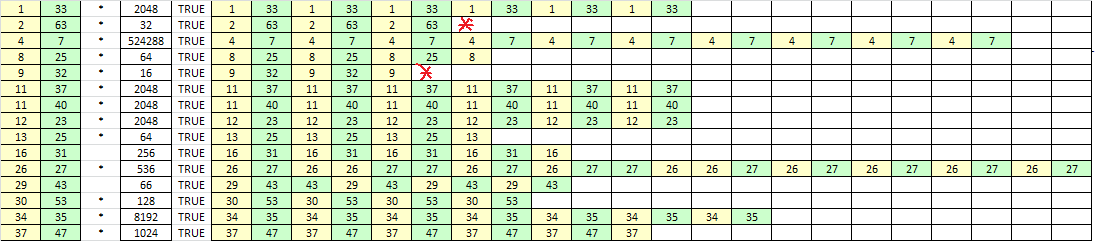
a, : 1,8,14,43,47,40,51  (1,8,14,40,43,47,40,51,1,8,43,14,43,47,40,1,40,47,43,51,1,8,14,43,47,40,51,1,8)
l, : 2,52,56,57  (2,2,2,52,2,56,57,2,52,57,56,56,2,2,57,56,2,57,52)
t, : 3,6,19,23,35,38,41  (3,6,19,23,35,38,41,3,6,19,23,35,38,41,3,6,19,23,35,38,41,3,6,19,23,35,38,41,3,6,19,23)
h, : 4,36,39  (4,4,36,39,36,4,36,39,39,36,36,36,4,36,36,39,4,36,36,39,4,36,39,4,36)
e, : 34,48,10,42,5  (5,10,34,10,10,42,34,48,10,10,34,42,34,5,34,42,48,48,5,34,10,10,42,5,42,34,42,48,48,48,10,42,42,5,10,5,34,34,10,48,10,5,42,5,34)
r, : 7,25,46,49  (7,25,46,49,7,46,25,46,49,7,25,49,46,7,49,49,7,49,25,46,49,7,25)
c, : 9,26,30  (9,26,30,9,26,30,9,26,30,9,26,30)
s, : 11,29  (11,29,11,29,11,29,11,29,11,11,29,11,11,29,11,29,11,11,11,29,11)
o, : 12,24,27,32  (12,24,27,32,12,24,32,27,32,12,32,24,27,32,12,24,27,32,12,24,32,27,32,12)
f, : 13,15,16  (13,15,16,13,15,15,16,13,15,16,13,15,16,13,15)
i, : 17,22,31  (17,17,22,31,31,31,17,22,31,17,22,31,31,17,22,31,17,31,22,22)
n, : 18,28  (18,28,18,18,28,18,18,28,18,18,28,18,18,28,18,28,18,28,18,28)
y, : 20  (20,20,20,20,20)
w, : 21  (21,21,21,21,21,21,21,21)
u, : 33  (33,33,33,33,33,33,33,33,33)
b, : 37,58  (37,58,58,37)
d, : 44  (44,44,44,44,44,44,44,44,44,44)
v, : 45,50  (45,50,45)
m, : 53,62  (53,62,53,62,53)
p, : 54,55  (54,55,54,55)
g, : 59,60  (59,60,59,60,59)
k, : 61,63  (61,63)

The "hillclimber" didn’t do nearly as well to find the cycles:

See: viewtopic.php?f=81&t=267&start=70, post # 2, p44.txt (this is Experiment 3 J-ST, or "Experiment 3").

With Experiment 2, 23 out of 63 of my potential merges would have been accurate. With Experiment 3, only 11 of the potential merges would have been accurate.

Low scores may be as relevant as high scores. The two M’s were pushed together with a score of only 16, and the two V’s with a score of only 4. When I post the short list for the 340, scores may not matter much.

I created an easier 45-symbol cipher to see if results will improve:

Seems to be a reasonably interesting cipher, bigram counts for directions are somewhat equal!

p17.txt
-----------------
Symbols: 45
Characters: 340
Multiplicity: 0.1323529
Sum of non-repeats: 5790
Index of coincidence: 0.0206316
-----------------
Symbols numbered by order of appearance:
-----------------
1 = % (c=3)
2 = " (c=8)
3 = 8 (c=10)
4 = i (c=9)
5 = b (c=7)
6 = j (c=9)
7 = D (c=8)
8 = q (c=8)
9 = M (c=8)
10 = * (c=9)
11 = [ (c=10)
12 = V (c=9)
13 = X (c=9)
14 = L (c=8)
15 = Z (c=6)
16 = 3 (c=9)
17 = A (c=9)
18 = Q (c=10)
19 = K (c=7)
20 = Y (c=8)
21 = g (c=9)
22 = 5 (c=6)
23 = d (c=9)
24 = G (c=8)
25 = s (c=9)
26 = u (c=8)
27 = C (c=7)
28 = H (c=8)
29 = ' (c=9)
30 = 1 (c=7)
31 = : (c=7)
32 = ( (c=9)
33 = x (c=7)
34 = 4 (c=5)
35 = J (c=7)
36 = o (c=8)
37 = p (c=9)
38 = v (c=7)
39 = c (c=1)
40 = l (c=7)
41 = I (c=8)
42 = w (c=6)
43 = N (c=5)
44 = F (c=6)
45 = 2 (c=4)
-----------------
Symbolic cipher:
-----------------
%"8ibj%DqM*[VXL"Z
3AQKYg5dGsuCH'51:
*(LA53x4dJoD8spv*
iA(j43[Qcl5dgXMqI
o8i"X4'ws(p8GJ[ou
%DqC*QVX1"N3AgFY'
JjvLDZdspHu[GIu"K
Fj*(QqK1NDgLA'qxw
G"VD:H1Zpl[2QIjbF
LYsM:vgGwKjqiClo8
'2pVjbH[1*3vQYAIi
j:sdgloX(xYJi*3'V
b"H8:dMlbICwpA([b
VxvQNHoiJs3guDX'I
LFqMKpYV[GH"q*dQC
IuF1Jx8Z(gLw:4oX2
'VAM8Np2[XJCv8xZ3
s*ibHMNdAwGj5(CKQ
3o5Fliu1XZDxYd4gL
:'KplYI[8vs(QGMVu
-----------------
Nummeric cipher:
-----------------
1,2,3,4,5,6,1,7,8,9,10,11,12,13,14,2,15
16,17,18,19,20,21,22,23,24,25,26,27,28,29,22,30,31
10,32,14,17,22,16,33,34,23,35,36,7,3,25,37,38,10
4,17,32,6,34,16,11,18,39,40,22,23,21,13,9,8,41
36,3,4,2,13,34,29,42,25,32,37,3,24,35,11,36,26
1,7,8,27,10,18,12,13,30,2,43,16,17,21,44,20,29
35,6,38,14,7,15,23,25,37,28,26,11,24,41,26,2,19
44,6,10,32,18,8,19,30,43,7,21,14,17,29,8,33,42
24,2,12,7,31,28,30,15,37,40,11,45,18,41,6,5,44
14,20,25,9,31,38,21,24,42,19,6,8,4,27,40,36,3
29,45,37,12,6,5,28,11,30,10,16,38,18,20,17,41,4
6,31,25,23,21,40,36,13,32,33,20,35,4,10,16,29,12
5,2,28,3,31,23,9,40,5,41,27,42,37,17,32,11,5
12,33,38,18,43,28,36,4,35,25,16,21,26,7,13,29,41
14,44,8,9,19,37,20,12,11,24,28,2,8,10,23,18,27
41,26,44,30,35,33,3,15,32,21,14,42,31,34,36,13,45
29,12,17,9,3,43,37,45,11,13,35,27,38,3,33,15,16
25,10,4,5,28,9,43,23,17,42,24,6,22,32,27,19,18
16,36,22,44,40,4,26,30,13,15,7,33,20,23,34,21,14
31,29,19,37,40,20,41,11,3,38,25,32,18,24,9,12,26
-----------------
Nummeric cipher for ZKDecrypto:
-----------------
1   2   3   4   5   6   1   7   8   9   10  11  12  13  14  2   15  
16  17  18  19  20  21  22  23  24  25  26  27  28  29  22  30  31  
10  32  14  17  22  16  33  34  23  35  36  7   3   25  37  38  10  
4   17  32  6   34  16  11  18  39  40  22  23  21  13  9   8   41  
36  3   4   2   13  34  29  42  25  32  37  3   24  35  11  36  26  
1   7   8   27  10  18  12  13  30  2   43  16  17  21  44  20  29  
35  6   38  14  7   15  23  25  37  28  26  11  24  41  26  2   19  
44  6   10  32  18  8   19  30  43  7   21  14  17  29  8   33  42  
24  2   12  7   31  28  30  15  37  40  11  45  18  41  6   5   44  
14  20  25  9   31  38  21  24  42  19  6   8   4   27  40  36  3   
29  45  37  12  6   5   28  11  30  10  16  38  18  20  17  41  4   
6   31  25  23  21  40  36  13  32  33  20  35  4   10  16  29  12  
5   2   28  3   31  23  9   40  5   41  27  42  37  17  32  11  5   
12  33  38  18  43  28  36  4   35  25  16  21  26  7   13  29  41  
14  44  8   9   19  37  20  12  11  24  28  2   8   10  23  18  27  
41  26  44  30  35  33  3   15  32  21  14  42  31  34  36  13  45  
29  12  17  9   3   43  37  45  11  13  35  27  38  3   33  15  16  
25  10  4   5   28  9   43  23  17  42  24  6   22  32  27  19  18  
16  36  22  44  40  4   26  30  13  15  7   33  20  23  34  21  14  
31  29  19  37  40  20  41  11  3   38  25  32  18  24  9   12  26  
-----------------
Symbolic cycles:
-----------------
Old symbol: j, homophone(s): %  (%%%)
Old symbol: u, homophone(s): "D  ("D"D"D"D"D"D"D"D)
Old symbol: n, homophone(s): 8X  (8X8X8X8X8X8X8X8X8X8)
Old symbol: o, homophone(s): io  (ioioioioioioioioi)
Old symbol: b, homophone(s): b  (bbbbbbb)
Old symbol: y, homophone(s): j  (jjjjjjjjj)
Old symbol: p, homophone(s): q  (qqqqqqqq)
Old symbol: i, homophone(s): MCx  (MCxMCxMCxMCxMCxMCxMCxM)
Old symbol: t, homophone(s): *As  (*As*As*As*As*As*As*As*As*As)
Old symbol: e, homophone(s): [Qg'p  ([Qg'p[Qg'p[Qg'p[Qg'p[Qg'p[Qg'p[Qg'p[Qg'p[Qg'p[Q)
Old symbol: r, homophone(s): VHI  (VHIVHIVHIVHIVHIVHIVHIVHIV)
Old symbol: a, homophone(s): LG1  (LG1LG1LG1LG1LG1LG1LG1LG)
Old symbol: g, homophone(s): ZN  (ZNZNZNZNZNZ)
Old symbol: h, homophone(s): 3d(  (3d(3d(3d(3d(3d(3d(3d(3d(3d()
Old symbol: l, homophone(s): KF  (KFKFKFKFKFKFK)
Old symbol: s, homophone(s): Y:l  (Y:lY:lY:lY:lY:lY:lY:lY)
Old symbol: w, homophone(s): 5  (555555)
Old symbol: f, homophone(s): u  (uuuuuuuu)
Old symbol: c, homophone(s): 4  (44444)
Old symbol: m, homophone(s): J  (JJJJJJJ)
Old symbol: d, homophone(s): vw  (vwvwvwvwvwvwv)
Old symbol: k, homophone(s): c  (c)
Old symbol: v, homophone(s): 2  (2222)
-----------------
Nummeric cycles:
-----------------
Old symbol: j, homophone(s): 1  (1,1,1)
Old symbol: u, homophone(s): 2,7  (2,7,2,7,2,7,2,7,2,7,2,7,2,7,2,7)
Old symbol: n, homophone(s): 3,13  (3,13,3,13,3,13,3,13,3,13,3,13,3,13,3,13,3,13,3)
Old symbol: o, homophone(s): 4,36  (4,36,4,36,4,36,4,36,4,36,4,36,4,36,4,36,4)
Old symbol: b, homophone(s): 5  (5,5,5,5,5,5,5)
Old symbol: y, homophone(s): 6  (6,6,6,6,6,6,6,6,6)
Old symbol: p, homophone(s): 8  (8,8,8,8,8,8,8,8)
Old symbol: i, homophone(s): 9,27,33  (9,27,33,9,27,33,9,27,33,9,27,33,9,27,33,9,27,33,9,27,33,9)
Old symbol: t, homophone(s): 10,17,25  (10,17,25,10,17,25,10,17,25,10,17,25,10,17,25,10,17,25,10,17,25,10,17,25,10,17,25)
Old symbol: e, homophone(s): 11,18,21,29,37  (11,18,21,29,37,11,18,21,29,37,11,18,21,29,37,11,18,21,29,37,11,18,21,29,37,11,18,21,29,37,11,18,21,29,37,11,18,21,29,37,11,18,21,29,37,11,18)
Old symbol: r, homophone(s): 12,28,41  (12,28,41,12,28,41,12,28,41,12,28,41,12,28,41,12,28,41,12,28,41,12,28,41,12)
Old symbol: a, homophone(s): 14,24,30  (14,24,30,14,24,30,14,24,30,14,24,30,14,24,30,14,24,30,14,24,30,14,24)
Old symbol: g, homophone(s): 15,43  (15,43,15,43,15,43,15,43,15,43,15)
Old symbol: h, homophone(s): 16,23,32  (16,23,32,16,23,32,16,23,32,16,23,32,16,23,32,16,23,32,16,23,32,16,23,32,16,23,32)
Old symbol: l, homophone(s): 19,44  (19,44,19,44,19,44,19,44,19,44,19,44,19)
Old symbol: s, homophone(s): 20,31,40  (20,31,40,20,31,40,20,31,40,20,31,40,20,31,40,20,31,40,20,31,40,20)
Old symbol: w, homophone(s): 22  (22,22,22,22,22,22)
Old symbol: f, homophone(s): 26  (26,26,26,26,26,26,26,26)
Old symbol: c, homophone(s): 34  (34,34,34,34,34)
Old symbol: m, homophone(s): 35  (35,35,35,35,35,35,35)
Old symbol: d, homophone(s): 38,42  (38,42,38,42,38,42,38,42,38,42,38,42,38)
Old symbol: k, homophone(s): 39  (39)
Old symbol: v, homophone(s): 45  (45,45,45,45)

Whoa Jarlve. Hang on a bit. I very much appreciate the new cipher, but hang on a bit. My spreadsheet is set up for 63 symbols; it’s not as versatile as your computer programs and would take a bit of overhauling. But the Mystery Cipher is easier than Experiment 3 anyway.

I am working on the Mystery Cipher and tuning my cycle finding skills. I am going to post some interesting results soon, and will compare Exper. 2, Exper. 3, the Mystery Cipher, and the Z340.

I am really sort of fascinated that some of the shorter two symbols cycles are getting flushed out, because there are so many dozens of short two symbol cycles that are false. But I am thinking that even though all we have is 9, 32, 9, 32, 9, 32 for example in the Mystery Cipher, symbols 9 and 32 don’t cycle better with any other symbols so they flush out. We have been assuming that long perfect cycles are the most reliable, but I am not so sure that there is a straight line relationship between length, perfectness, and true or false. The symbol count and interrelationships of all of the symbols are factors.

I’ll show a long false cycle created by the overlapping of true cycles. And I am going to compare the first and second halves of Exper. 2, Exper. 3, the MC and the 340 with a simple distribution of scores.

You’ll see. I was thinking about asking for you to create some new messages for me last night. But I want to work with the material that I have for a bit, get as much mileage out of the existing experiments as I can while I tune my system. Hang on. I can hardly wait to get through this so that I can try your new program. I wonder if it will work better than ZDK when expanding suspected wildcards into multiple symbols.

Smokie

Alright, so here are the cycle hillclimber scores that I did not publish yet:

340: 250900
Ex2: 1436749500
Ex3: 184240
MYC: 5605760

The Mystery Cipher cycles perfectly, but has what you called subtle columnar transposition. Ex2 cycled perfectly. And Ex3 had several cycles with a lot of randomization. The scores might suggest that the 340 is maybe a little bit more perfectly cycled than Ex3.

Here’s the Mystery Cipher, where I found 15 true merges and quite a few false merges, of which I only show a sample).

See: viewtopic.php?f=81&t=267&start=80, post # 5, and viewtopic.php?f=81&t=267&start=90, post # 1 (this is the "Mystery Cipher").

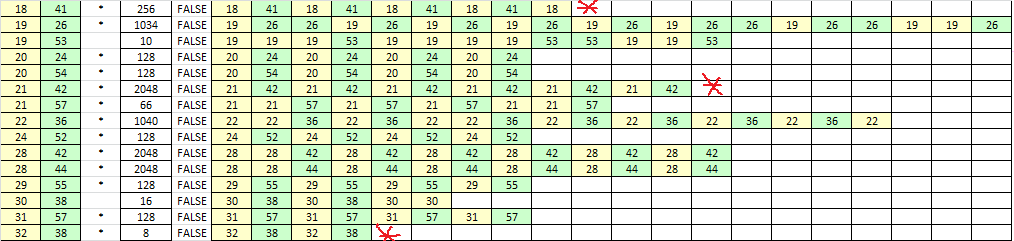
Here are the true cycles where I marked a couple of low count short cycles were flushed:

And here is a sample of the 47 other false cycles, where I marked a long and short false cycle:

So I am trying to figure out if there is anything remarkable with all of this. It’s a work in progress. I still haven’t published my short list for the 340; not yet because it may change. One thing that I did learn with the Mystery Cipher is to look at each individual cycle flushed by the hillclimber and judge for myself whether there is cycling or not. Sometimes there is no cycling at all; two symbols sit next to each other and serve as a break between two other cycles, whether true or false. I learned to shorten my short list, and may be able to boil down a list of maybe 30 possible merges, of which half are true.

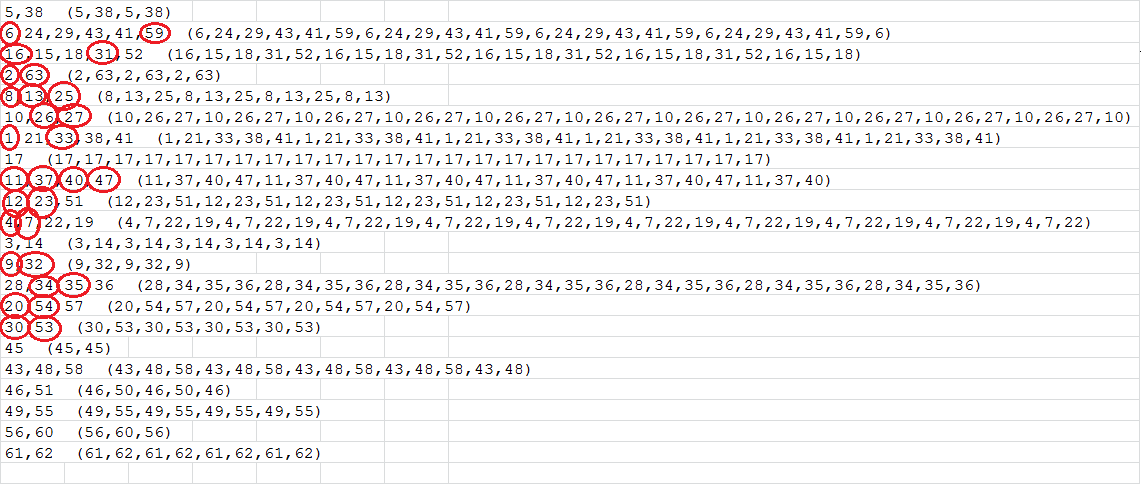
Here’s the cycles found in the Mystery Cipher by your table:

See: viewtopic.php?f=81&t=267&start=80, post # 5, and viewtopic.php?f=81&t=267&start=90, post # 1 (this is the "Mystery Cipher").

And here is an example of how two cycles can overlap to create a false cycle in the Mystery Cipher:

I show 6 24 29 43 41 59 as A B C D E F and 16 15 18 31 52 as a b c d e. They make false cycle 18 41 = cEcEcEcEc, which the hillclimber flushed out. There is obviously a lot of that happening in the 340.

Jarlve, if you want, you can make one with a little bit of randomization. Try to emulate the 340 by randomizing a bit less than Experiment 3. Maybe randomize toward the end like the 408? See if I can make a short list of possible merges where some are true, in an experiment where I don’t know the answers. But it would be nice to have 63 symbols. Only if and when you have time. Otherwise I’ll work on looking at halves with simple score distributions. I don’t have to overhaul my spreadsheets for that.

Smokie

I doubt that I am the first to try this, but here are the first half – second half cycle stats for four messages:

1. The 340, Ex2 and Ex3 have more cycling in the first half than the second half.

2. Should we take into consideration that starting at row 11, column 1 will cut a lot of cycles in half? On the other hand, ending at row 10, column 17 cuts top cycles in half also. Experiment 2 was pure cycles, and has more cycles in the first half than the second half, so at first I am inclined to say that starting at row 11, column 1 has an effect.

3. Except when you look at the Mystery Cipher, which inexplicably has more cycles in the second half than the first half. Jarlve made the Mystery Cipher perfectly cyclic and included only one high count symbol, 17, with count of 24.

4. The 340 numbers more closely resemble Experiment 3, where Jarlve randomized several of the cycles pretty good. But Experiment 3 has only three 1:1 ( 21, 33 and 41) with high count, total count of only 27. The 340 has a somewhat different structure, with four high count 1:1 or whatever they are ( 5, 19, 20 and 51), total count of 57.

In conclusion, the 340 has more cycling in the first half, which may be caused by cutting cycles in part at row 11, more randomization in the second half, false cycles created by overlapping cycles and which fizzle out, or some combination of the three.

I love these results!

They do somewhat confirm that the 340 has no columnar transposition going on after encoding, since the Mystery cipher is just that and that seems to juggle the cycles around awkwardly.

It’s true what you say smokie, that cycles are interrupted starting at row 11. But if the 340 is a 2 part cipher and the encoding started anew at row 11, we probably would see halves that are about equal. For now it seems that the 340 correlates best to the cipher with some randomization in the cycles and a few 1:1’s.

I’ll create a cipher which is more prone to randomization in the cycles near the end. Give me some time.

Thanks, Jarlve. I know that you are trying to do a lot of things right now, so whenever you get the chance is fine.

EDIT:

Just want to note that smokie’s latest work on the ciphers in viewtopic.php?f=81&t=267&start=160 (his last post) also seems to add evidence against columnar transposition being actual after encoding for the 340. It seems to juggle the cycles around, though it’s certainly not conclusive until someones decides to do a really big test to see what actually happens to the cycles with columnar transposition after encoding.

Jarlve, if you want me to, I can produce these simple two symbol cycle stats for different test messages, and line them up side by side with the 340. I can include whole, first half, and second half stats. You can make changes to the messages and I will show what happens to the cycle stats. You don’t have to tell me what you did beforehand, and I won’t try to solve them.

Maybe that will help to clear things up about whether Zodiac rearranged the ciphertext after encoding or any other questions that you may have. And maybe someone who finds interesting results can later take the baton and perform more sophisticated testing.

When and if you want to.

I think that the cycles are a gift. Maybe we will never be able to sort all of the Zodiac made cycles from the random cycles or the cycle overlap made cycles (I think there may be a difference between the two). But maybe studying the cycle stats will help us figure out what the 340 really is.

I also am thinking about a new idea for scoring two symbol cycles. Just a rough draft of an idea. But with my spreadsheet I think that I can easily identify the start and end positions of each cycle. There may be a lot of different ways to use that information. For instance with cycle type ABABAB, distance and mean distance between start and end position, mean start position, mean end position, first half only, second half only, other? Can there be some meaningful use for the information? Is a cycle ABABAB that starts in row 1 and ends in row 10 any more or less likely to be Zodiac-made than a cycle that starts in row 1 and ends in row 20? Can test messages be used to figure that out? Other questions?

Like I said, a rough draft of an idea, and I’ll have to work on that later. I may be setting myself up for a lot of fun work when I have other obligations.

Yes, the cycles are very much a gift. I think your distances idea could be very fruitful, it’s something I was planning to do myself eventually. On average a true cycle should be more equally spread throughout the cipher. I have such a measurement for individual symbols and it really does show that in a cyclic cipher the symbols are more equally spread throughout the cipher.

Obligations come first, take your time, no strings attached!

Yes, I see what you mean.

A…..B…..A…..B…..A…..B is more likely a true cycle compared to A..B…….A………………B..A………………..B.

That makes sense because of plaintext frequencies. I will definitely have to explore that concept, perhaps with my hillclimber. I could just make a new scoring formula and try it out on different messages. See if the hillclimber flushes out more or fewer true cycles.

Thanks for the input!

A…..B…..A…..B…..A…..B is more likely a true cycle compared to A..B…….A………………B..A………………..B.
That makes sense because of plaintext frequencies.

I don’t quite follow everything you guys are doing here, so apologies if I misunderstood what you meant, but I don’t think it’s quite true what you just said. It would be, if the letters were evenly distributed throughout the plaintext, but they are usually not, for an average English text.
For example, take your last sentence. I’ll highlight all E’s: "thatmakEssEnsEbEcausEofplaintExtfrEquEnciEs", or "…….E..E..E.E….E……..E….E..E…E.". Very uneven distribution.
It is even more so for the letter S: "……..SS..S……S………………….S.."