I will work on a hill climber that scores candidate wildcard substitutions.

That’s nice to hear! I really like to see the 340 solved so that we can all go home.

ZKDecrypto found a weak solve to the 408plusover after 17 minutes on my i5. Score 32066, quite readable actually. But it is only a 53 symbol cipher.

Using an IoC Weight of 6, ZKD converged in 90 seconds on a solution that is 56% accurate (on a recent i7):

ISIDADIESANGHETHEERSCAUREITINSOMUCHBUCISAIMOUEFUNTHANDIVEINGLISSSE
MEACTSABORDERTSECOUNSMANISTHEMTOTWANGESTUEENOMAEOFAVETODIVENTS
ETHISGGAPASSESHEMOOTTHRIVEINGSSHESENCEITARASENRETTSUTHECGETTINGYO
URDOCDNSBFLITHOGISSTHERESTHARTOBATIOTHEELHASSWIEALIVEREDSROUNSCHA
RELICEINWASSTHEAHSPEDISSALLIVERSSTMEMYRVOPSNILIESNOTGIPSYOUMYCAMERACAUSEYOULISVTUS

Using a different recipe ( ) , running ZKD for 90 seconds at an IoC Weight of 1, scrambling the key and then rerunning it for 90 seconds at an IoC Weight of 6, I got a 69% accuracy:

ALIDEDIDLINGPEOPDEBSCAUSEATITSOMUCHFURISIAMOIERUNTHANDANDINGWILSSE
MEIRTSEFORCESTSECUUTSMANASTHEMOUTHANGESTUEENUMADORANDTODINDTOS
ETHISGGIVESSESHEMOUTTHRANDINGSSPESENCEITISESENBETTSITHERGETTANGYOUR
COCDTSFRWITHUGISLTHEBESTPARTOFITAUTHEEWHESSHIEIWANDBECSBOINSRPARELICE
ANHALLTHEIHSVEDALSELWINDBSSOMEMYSNUVSTAWADLNOTGIVSYOUMYRAMEBECAUSEYOUWALNTIS

"5", which I call symbol 50, appears 11 times in the message, but does not cycle with any other symbol in a high scoring sequence.

Symbol number 50 by order of appearance only appears 7 times. The only symbol that appears 11 times is number 5.

So your list of possible wildcards would be (symbol number by order of appearance): 5, 19, 20 and 51. Right?

Thanks!

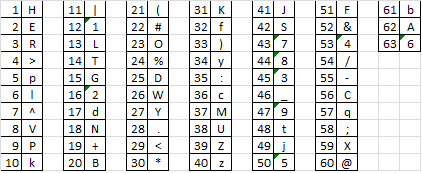
K hang on. I have to convert stuff. I have Excel and use numbers. Let me straighten this out first. Here is a conversion chart that I just made:

Yes, you are correct. Symbol 50 appears 7 times. And I sincerely apologize for the mistake. Nevertheless, I will post my some of my work and explain what I was thinking. Perhaps it will help.

S.T.

Here’s a cipher I had created in an older thread on polyphones (http://www.zodiackillersite.com/viewtopic.php?f=81&t=261) :

O9PP5o97W`flWZ8Om
AQ+@@kAh8OEW9Mg0
nKh8+D7NRVe=anVD
`SLia:C7oX0@++ZDi
`fR+b0X?dKk?+E8LV
7YMgcSNhZaE5o6EYZ
Mo+KM1ocgbm2[BZ8
dE1LZB`6+aCGU+f;K
jQ7+g+5]M?Dl;e1gf
FX@lO+4A+iCG`hj67
D+QAEgal2[jgAMLHW
ghCNB74hWIBoX+;C1
Z5RIB7+fIcgk=XAPH
OeENe7WBd@SRga]++
D9@bJ?a1`a9ih2+
8ga+WZoe`+L:mL?ea
++TIhWZBSoSY4=5NX
Kh3[CH0?E9^de=oCC
Mik2SYZ7gBL[BPXB@
4eh3_=[R[ELYPVb+

It has 63 symbols, a frequency distribution similar to the z340 and a length of 340 characters. I used the + symbol as a wildcard and placed them in exactly the same position as in the z340. ZKD is easily able to decrypt the text.

Thanks for the cipher _pi. It is suggested that up to 4 or 5 symbols could possibly be wildcards.

Thank you smokie, take your time.

O.k., I have an Excel spreadsheet with all of the two symbol sequences. All of the two symbol sequences are included in the sequences that are more than two symbols (e.g., ABC would include AB and AC). So I can see patterns without looking at a lot of noise by looking at two symbols at a time.

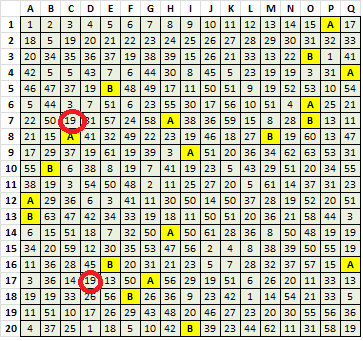
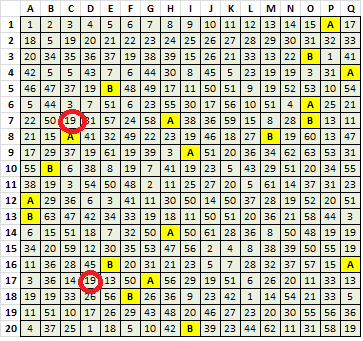
Below is a spreadsheet showing the symbol number, quantity, a total score, and the number of sequences that it appears in with a total score of 50% or more.

On the right, in purple, are the scores of that symbol when included in a prospective sequence with all of the 62 other symbols.

ABAB would have a score of 50%, because only two symbols, the second and third, are bracketed by the symbols that they should be bracketed by if the sequence is perfect. The scoring system is crude, but takes into account the total length, and whether there are missing symbols. ABABABAB*B would have a score of 70%.

Obviously with the mathematical error with symbol 50, there is an error with one or more symbols also. I am a bit embarrassed. However, look at the spreadsheet in its entirety. There are some symbols that appear many times. Those symbols are among the lowest scoring, and do not really appear in any high scoring sequences. The symbols that appear fewer times generally appear in higher scoring sequences.

For instance, symbol 19, the "+", appears 24 times. But it does not appear in any good sequence with another symbol. None get a score of even 50%. Note that in the distribution chart that I posted above, there is a shift at the 50% score mark, where the Actual 340 has twice as many sequences that score at 50% than the Randomized 340. Here are the first few sequences for Symbol 19, or the "+":

O.k. now to Symbol 5, the "q" appears 11 times. But it only appears in two sequences that score to higher than 50%.

I will continue on to post the top scoring sequences for Symbols 20 and 51. Sorry about the error. I will have to find out which other symbols are incorrect because of this.

S.T.

Here is Symbol 20, the "B", which appears 12 times, and only appears in three "sequences" that score higher than 50%. You can see that even those sequences don’t even look like any pattern at all.

And Symbol 51, the "F", appears 10 times, and again, appears in only two "sequences" that score higher than 50%. No pattern really.

O.k., so if you make 5, 19, 20 and 51 ( "q", "+", "B", and "F") wildcards that could represent multiple letters as substitutes for other symbols in the sequences, does your computer program find any solution that is better than what you already had?

Do you want me to keep working on this? Find some sequences that have missing symbols and then show that 5, 19, 20 or 51 are going to appear where the missing symbol should be? There are a lot. The length of the string where the missing sequence symbol should be is important. I have some other spreadsheets that would help.

Do you want me to keep working on this? Find some sequences that have missing symbols and then show that 5, 19, 20 or 51 are going to appear where the missing symbol should be?

That would be perfect.

On the other hand, I think we also need verification of your find as first order of business. Because I suspect it might be very hard to recover the solution with 3 to 5 wildcard symbols with these counts. I’m hoping that doranchak, finder and _pi can jump in on the verification part. With verification I mean, is this find statistically significant? My intuition says yes, and this may be exactly what we have been looking for.

So if I may,

1. Verificate.
2. Come up with the best possible list of wildcard candidates and its symbol substitutes and share them so everyone can chip in.
3. Attack.

Doranchak has hinted writing a sophisticated hill climber. I think it might turn out to be a small nightmare to get it working. We may as well help him by creating some test ciphers that range from easy to hard.

I’m trying to find a way to cheat the problem. Perhaps by removing all wildcard symbols and try to nuke it out.

Thanks to everyone for their work so far.

Here are Symbols 16 and 40, the "2" and "z".

I just made the 16 an "A" and the 40 a "B" to show the pattern. You can see that Symbol 19, the "+", is there where the missing symbol should be.

This one example doesn’t prove anything. But much of the time when I put a sequence in the solving tool, one of the possible wildcard symbols appears where the missing symbol should be. Although that isn’t proof either, take also that the four possible wildcards do not cycle with other symbols, and that this is only a minor departure from how Zodiac ciphered the 408. It would make sense.

I took 30 samples from Zodiac’s letters 340 characters long each, and found the mean and standard deviation for the quantity of each letter. Then I total the number of symbols in the sequence, including the wildcards, and find the difference between that and the mean for each letter. Then I divide by the standard deviation for the letter, and rank the letters according to number of standard deviations from the mean, from lowest to highest.

In other words, there are a mean number of 21.5 H’s in 30 samples taken from Zodiac’s letters that are 340 characters long, with a standard deviation of 4.6. There are 22 symbols in the 16-40 sequence, including the wildcards. 22-2.15/4.6=0.11 for the letter H, which is the lowest number in standard deviations for all of the letters in the alphabet.

If my system is correct, Symbols 16 and 40, the "2" and "z", could be H, N, A, S, L, I, R, or O in that order of probability.

I have been working on this message for a while just to show the method, and looking at what Jarlve just posted, I may be getting ahead of myself.

But that’s my method.

Note that the 50 issue isn’t solved yet, and may take some time. Again, I apologize.

doranchak,

I wanted to look at your tables to find some of the higher scoring sequences with more than two or three symbols in them. I wanted to find some that have missing symbols and see if I can find if the wildcard symbols are where they should be. But I see that the tables for the L=4, L=5, L=6 and L=7 for the 340 are no longer on your website. Are you revising or deleting for some reason?

http://zodiackillerciphers.com/wiki/ind … es#L.3D3_2

Smokie

No – they are showing up for me.

L=5: P|YMZ, [P|YMZ] M| [P|YMZ] |YM|M|Z|M| [P|YMZ] |
…etc…

I wonder if the page load was just interrupted for you for some reason. Try it again – if the problem keeps happening, let me know. Maybe it’s a browser issue. What browser are you using?

Google Chrome, but I can see it now.

Again, thank you very much for making the tables.

I have to go outside and get some work done, but will be back.

I hope that you like my idea about the wildcard symbols.

Smokie

I’ve been thinking about the new search space.

Without wildcard symbols, the key search space is 26^63 (assuming that one key is the correct key and can be verified when it is examined).

With those 4 different symbols ( "q", "+", "B", and "F") acting as wildcards, there are 59 remaining symbols, but now there are 58 wildcard spots. Each wildcard spot can be assigned any plaintext letter. So now the search space has become 26^(59+58) = 26^117. It also raises the effective multiplicity to 117/340 = 0.34, which might be problematically high.

I’m not saying it’s impossible, or that it’s a bad idea. I’m just saying it’s… difficult.

I will work on a hill climber that scores candidate wildcard substitutions.

That’s nice to hear! I really like to see the 340 solved so that we can all go home.

What I mean to say is a hillclimber that considers symbol substitutes for the wildcards, measuring the effect such assignments have on the overall statistics and homophonic features.