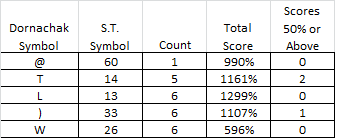
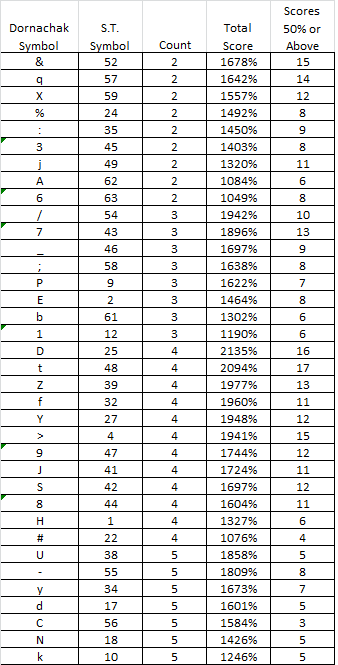
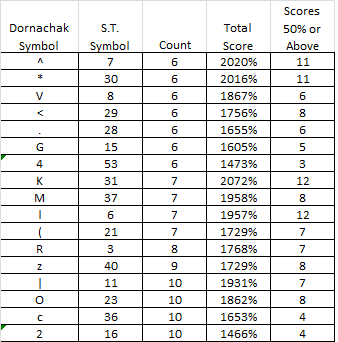
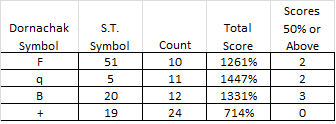
I am working on fixing my mistake with Symbol 50, and will post a new chart showing the total count and scores for each symbol.
I will also work up some sort of simple way to compare:
1. Symbols that are low in count and are not in sequences (score = low)
2. Symbols that are low in count and are in sequences (score = high)
3. Symbols that are high in count and are in sequences (score = high); and
4. Symbols that are high in count and are not in sequences (score = low and what I think may be wildcards).
By grouping the symbols this way and looking at how the groups compare to each other, maybe we can learn something else. I don’t know.
S.T.
O.k., here is my new chart.
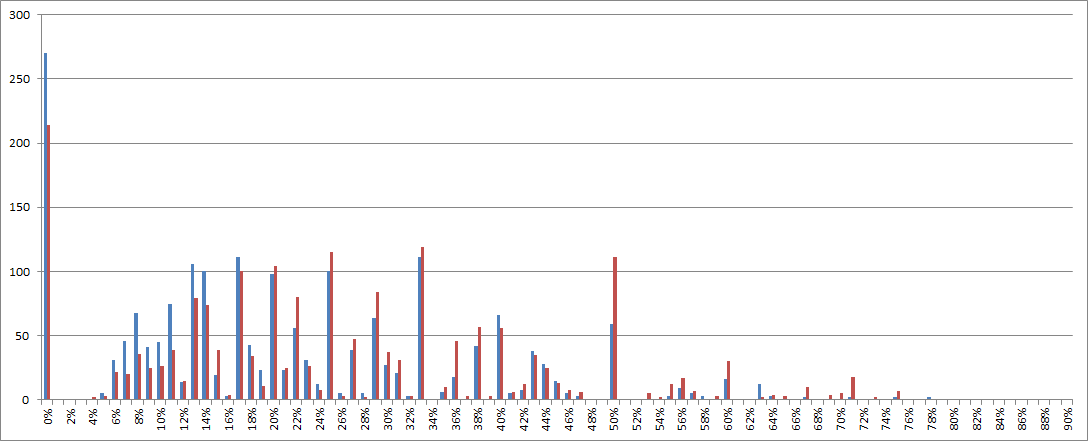
It shows the distribution of scores for each symbol as compared to every other symbol. Two symbol sequences only, as I think that initially that is all that is necessary. A symbol with a higher total score has more sequential relationships with other symbols. A symbol with a lower score will have fewer or no relationships with other symbols.
Next I will take out all of the stuff on the right and start grouping symbols according to score and count to show that some symbols are very different than others. Maybe this will help to verify whether there is any statistical significance in the data.
S.T.
1. Symbols that are low in count and are (probably) not in sequences (score = low)
Obviously Symbol 60, the "@", only appears once, and therefore could not be in any sequence.
2. Symbols that are low in count and are in sequences, depending on the count above 50% (score = high)
I am sure that you guys follow me, but I need to summarize for myself too.
1. Check out the distribution shift at the 50% score line when comparing Actual 340 scores and ONE randomized 340 score:
Because of this, and the fact that Zodiac used sequences in the 408, I am convinced that Zodiac used sequences in the 340. But many of the sequences in the 340 are also random. What needs to be done is randomize the 340 about 30 times, and make a distribution that shows means of the randomized scores. That will more clearly define a cutting off point and how we can calculate the probability that any two-symbol sequence is a Zodiac sequence or a random sequence.
2. Many of the longer sequences are most likely Zodiac sequences, because of their score. Also, almost if not all of them have missing symbols. I have looked at a lot of them, many which have more than two symbols, and there is often one of my proposed wildcard symbols found where it should be if substituted for a sequence symbol.
Now to argue against myself, there are a total of 57 of my proposed wildcard symbols in the message ("F" at 10 + "q" at 11 + "B" at 12 + "+" at 24 = 57), which makes the probability of this high. But, these wildcard symbols are high in count and do not sequence with other symbols well. If they did sequence with other symbols, then they wouldn’t be sitting next to each other, like the "qq" and "++". And, there are a lot of missing symbols in all of the high scoring sequences, collectively speaking.
3. This is the closest system to what Zodiac used with the 408. It is only a minor departure from his 408 system. In fact, he did use one or two symbols in more than one sequence in the 408. That’s what gave me the idea. See http://www.ciphermysteries.com/2011/09/ … 40-ciphers (the solid triangle cipher shape in Z408, and how it appears to encipher different letters at different times. The view often put forward elsewhere is that this varied due to copying errors, perhaps arising because the Zodiac Killer’s pen was too thick, causing him to misread his draft version).
It’s just a theory. But there is a statistical phenomenon with "F", "q", "B" and "+". There may be others. What about "C", my Symbol 56? That one doesn’t cycle well with any of the other symbols either.*
Similar to what Jarlve said, we can find some high scoring symbol sequences that have mostly mutually exclusive symbols that do not appear in other sequences (which is not easy, by the way – Zodiac may have had a complicated cycle system just to mess with our heads but with no message). Check to see what happens when looking for one of the missing symbols, and see if there isn’t a wildcard symbol there in the message.
A lot more work needs to be done, but this is my best guess as to what Zodiac did. He just decided to make the 340 more difficult than the 480, and substituted a bunch of wildcard symbols in the sequences.
We really need to sort through all of the sequences and figure out the probability of genuineness for each one. I suggest multiple randomizations of the 340 for comparison, which is beyond my skill level. Or what about just deleting the proposed wildcards, and possibly the "c" to see what happens then? What about finding the sequences that are most likely Zodiac made, and tallying up the number of missing symbols. Compare to the tally of wildcard symbols.
Any thoughts? Think about all of the different ways that we can figure this out if it is true.
Smokie
EDIT: Your symbol "C", which is my symbol 56, does cycle with your symbol |, which is my symbol 11, in the second half of the message. It could be a random coincidence.
Because of this, and the fact that Zodiac used sequences in the 480, I am convinced that Zodiac used sequences in the 340. But many of the sequences in the 340 are also random. What needs to be done is randomize the 340 about 30 times, and make a distribution that shows means of the randomized scores. That will more clearly define a cutting off point and how we can calculate the probability that any two-symbol sequence is a Zodiac sequence or a random sequence.
100 randomised 340’s. If you need anything else that can be achieved programmaticly let me know and I’ll see what I can do. I’m not a big fan of comparing the 340 to randomised counterparts because the 340 is not random at all.
2. Many of the longer sequences are most likely Zodiac sequences, because of their score. Also, almost if not all of them have missing symbols. I have looked at a lot of them, many which have more than two symbols, and there is often one of my proposed wildcard symbols found where it should be if substituted for a sequence symbol.
Yes that’s your theory, I guess doranchak is working on some kind of verification. I’m wondering if what you see could also be randomness in the cycle, because he did that in the 408 as well. For some time now I believed that some symbols are not part of the cipher because of a simple counting method (non-repeats) I came up with that can to some extent measure how cyclic a homophonic substitution cipher is. The theory I came up with is that the 340 is a word search and that some symbols are filler for the empty squares. So that’s why I want to have verification also.
In my thread a diagonal shift (highly experimental stuff in there) I did a crude test removing a random number of random symbols for a large number of iterations scoring the non-repeats and I came up with the following image showing the larger interruptions in the cipher as darker squares. Does it look familiar?

We really need to sort through all of the sequences and figure out the probability of genuineness for each one. I suggest multiple randomizations of the 340 for comparison, which is beyond my skill level. Or what about just deleting the proposed wildcards, and possibly the "c" to see what happens then? What about finding the sequences that are most likely Zodiac made, and tallying up the number of missing symbols. Compare to the tally of wildcard symbols.
I can do a crude test with the non-repeats.
The 340 scores 4462 normally, higher = more cyclic. I will attempt to normalise this number by the amount of symbols and characters.
After removing 5, 19, 20, 51: 6028! These symbols do interrupt the cycles.
After removing 5, 19, 20, 36, 51: 5941. I’m not convinced.
By the way this is the string of removed wildcards: "pp+BB+ppp+++F+pFF+++++FB++pFB+Bp+BF+FBF++B+Bp++FB++pFBBp+".
Haven’t had time to do statistical comparisons to random shuffles yet but I re-ran my brute force search for L=4 on Z340, Z408, and 3 shuffles of Z340.
Z340: https://docs.google.com/spreadsheets/d/ … sp=sharing
Z408: https://docs.google.com/spreadsheets/d/ … sp=sharing
Z340 shuffled #1: https://docs.google.com/spreadsheets/d/ … sp=sharing
Z340 shuffled #2: https://docs.google.com/spreadsheets/d/ … sp=sharing
Z340 shuffled #3: https://docs.google.com/spreadsheets/d/ … sp=sharing
Only sequences that occur at least twice are considered. The probability calculation is different this time. I simply computed the product of all the symbol frequencies divided by the cipher length (i.e., f1/340 * f2/340 * f3/340 … etc …).
Shuffle #1 seems to have some low probability cycles in it, so I’m curious what the statistics will end up showing if I run more shuffle tests.
The best pattern in Z408 shows up with probability 0 only because the float value was so low, it ended up getting rounded down to 0.
I guess in scientific terms, it is really a hypothesis because it is an explanation for observed phenomenon. What makes it attractive to me, besides that it seems to explain what I observe, is that it is not a big departure from the 408.
I sincerely appreciate your interest, and would not be disappointed at all if someone proves the hypothesis wrong. That’s how scientists work together.
However, you guys are really over my head with the computer programming. I wrote my own video game programs on a Commodore 64 many years ago, but then entered a different trade. So I understand a little bit about what you are doing. I also took statistics in college and got an A, and I know Excel very well from my former job. Those are my tools.
I get sucked into this stuff about once or twice a year. I just cannot let it go. I’ll find some more stuff to post in a bit, to sort of show you what I have been looking at after trying to find all of the sequences manually. ![]()
Smokie
O.k., I have been working on a few examples of my observations.
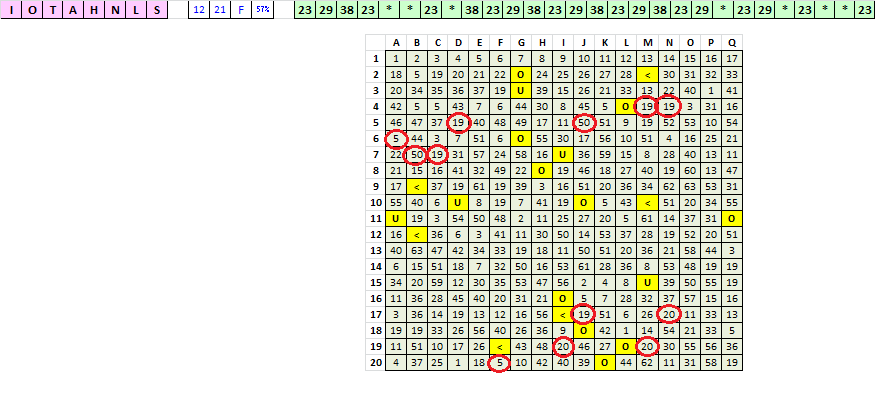
Symbols 23, 29 and 38 ( O,<,U ) all cycle with each other really well in a multi repeated sequence, but there are missing symbols. There are Symbols 5, 19, 20 and 50 in places where the missing symbols should be.
I’ll be back later.
S.T.
It certainly is a hypothesis worth exploring further.
So, I ran a quick experiment. In the 340, the cycle "RlNZ" appears, like this: [RlNZ] lR [RlNZ] RlRlRN [RlNZ] [RlNZ]. In my list of 4-symbol cycles ( https://docs.google.com/spreadsheets/d/ … =892030580), the "RlNZ" cycle is the best one, because the relative probability based on symbol frequencies is the lowest in the entire list: 4.93E-29. The number 4.93E-29 is not meant to convey the exact probability that the sequence occurred; instead, it is meant to convey that it is less probable to occur by chance than the other sequences.
That cycle seems rather strong, like it might be intentionally created by the cipher author.
I wanted to answer this question: How many times do you have to shuffle the 340 ciphertext before a sequence with similar relative probably appears completely by chance? I.e., how many shuffles does it take before you reach a probability estimate equal to or less than the best one in the 340 for L=4?
Well, I coded it up and it took only 11 shuffles:
Symbols: #5kN
Sequence: 5 [#5kN] [#5kN] # [#5kN] 55Nk [#5kN]
Shuffled ciphertext:
|y2BcMcXG(98BcU9F BF*6CTKVEM+Z)q<Y8 5;/c1JM^(#Fl9KD<R )+C)5p-CLzlV.p2HR 2/ZpRB:>+yMkKU/4^ (_dSbZBB+NEt|dWzd &PL6c+B#5K.BCPqkH PO++^>p*NKLVYppB6 f#|lG7cFOF#|W<%|Z OS8-75G.2EJO+R4R+ 4(G2pYR-jt-:+kzj* |+|z*NYVX1c.Jz2pz )OlFd|2+.l;%p5O+T BF3Azy<ffM@<+TO+W -9)t(C+Hp.MADK+G7 llO;+|^(F8zWVV+cB 5WD2_MTFOFpcWdy>U b31NKtTJ424y+SkS# >LB+5^_<+k*R^OLRU +b&zc|G*f(+4ULDNH
I was surprised how few shuffles were required, so I ran it again, and it took only one shuffle!
Symbols: .^Gy
Sequence: [.^Gy] [.^Gy] .G.^ [.^Gy] yG [.^Gy] ^
Shuffled ciphertext:
O.A^BU/Tt+<FG#|Fy 4.TY_4%2cZkzXMW21 (#7cWl)M*8+p2^BNC +YljKdJp962cRN#k( VzG-LF<(>U+ydZNR. p+VGc>+P|zbOT*|5. +HSZF^*++|UKfBB-F .YKk)+C_5+Y++J27z dMW|*9OFO:)PETFB| LW(p6(3VK&t|c-Ep< f5FCz8z/R;pR&Sc9q L+5-<(<dfAcR8ODOC tBWSj^NlBb|5lO4Vk +%#E+JR-tppPD+l/6 OLOU<(WG8MKyzpB*B K+f):5S75LT>y;+b+ 1FJXql4)_cVG+R+p+ L4RNOk+2c4lUzH.C3 #BD;1MpMB*9ZHH^|2 MGVcK2@2Fy^d>Bz|D
Ran shuffles one more time, and it took only 7 tries:
Symbols: 9^lG
Sequence: Gl [9^lG] [9^lG] G [9^lG] ^ll [9^lG] ^
Shuffled ciphertext:
dMGl>#3F*.CqOcpBd p%(cR9dF+BKT;@fp_ N4.D|p6_CXT-<zY+^ OyV2Oz+V;KL6l)+EA F+%TWSWMG4pkUFV8L 1W(9|WZzO5+^pc/7S <+2D-H2*>>qt62BBp M&+(-)l|.-pG5FcR* M)YSEt(5t2N7T+KbH G)394AKpy#4Ht4(N2 8HFN#VUW^|OU*V+<# z1WUR|cBy/JBkcD(: -2yk#*_z|J&zPl|)K KzD4++ZOObF|G.+C+ J+Y^CCFORcbc+:zT5 F>2l.L5KcNl5fF|dd k|/V<RMf9S^+lL<52 yBOEGc+PLXL;pZBzY 8UBRpP<+Rj++R8+MO ^j*Jf.+ZB(+7kBM1B
So – I’m back to the question: Are the sequences we’re seeing random or intentional cycles? I think you are right, that we need to compare the cycle score distributions of shuffled vs original.
It could also be the case that the cycles simply don’t appear strong, due to being interrupted by the wildcard symbols.
The situation is a little different with L=3, because the cycle l*M, which appears almost perfectly as [l*M] [l*M] [l*M] lM [l*M] [l*M] [l*M], has a much lower relative probability (1.7517163E-31) than any of the L=4 cycles.
To get an equally good or better sequence to appear randomly, I had to run 584 shuffles:
Symbols: ^K5
Sequence: [^K5] [^K5] 5K [^K5] [^K5] [^K5] [^K5]
Shuffled ciphertext:
<kd+M6W+M7q9PBczW O^:K(L4%+Cy+RcJJk TR||zbO2TpB/>-t+5 2<Zd+&lM<WcLZ+.M+ yE2z+k<^-G6jK+B<L ;-Y|j(+)-lpTXFt5. X|pU.BA6JMcH>cbCF *+k1OOR8Dfzzp.2(O d5LU++SKBtcP(WTG# ^K>EO/+5*N3+^T9#D 7z2MF)U+yGNG)_cY1 F3Z9lF/8(RUKF8D)B dRBVlFHV>VOVf(Bq* UN+48B-CPAdMcy2p& |zRblVSOB|Nl#.C5+ W%)D4Y^*+Kk4Oyc.t ;|OE|J2#LpS7Flfcp 5F;ZpzG*p2_H|LN+W VBB^H+p*GSz+(RC44 :_KR|<@#p92f15+FY
O.k. I realize that the first order of business is to verify once and for all whether Zodiac used sequences in the 340. Your most recent results are very exciting.
You found what I call sequence 6 30 37. I have a score of 80% for that with my rudimentary system.
Note that my * in the top green shaded string of symbols is for the wildcard, and it is not a symbol.
See that there are several wildcards in the string where the missing 30 (or your "*") should be.
I am saying that if this sequence is Zodiac made, and the wildcard hypothesis is correct, then those symbols should represent H, N, S, L, A, R, I, O, in that order of probability.
Again, the first order of business is to show one way or the other if Zodiac used sequences.
The rest of my hypothesis can be worked on later; the above serves to illustrate what I was talking about.
Thank you so much.
Smokie
The 340 uses cycles.
Ran a couple of tests with 10 million randomisations each counting the non-repeats and the highest I’ve gotten was 4350, on average 2950 or so. In the results that were the highest the "+" symbol was contributing towards the cycles. Just saying that if the 340 per chance would have bumped to 4462 where it is now, I guess it will also be likely that the higher frequency symbols would count towards that (which is not the case for the 340). Maybe there’s almost as much chance for outliers to occur in a randomised counterpart just by the sheer amount of combinations your checking… Take any shuffle and I bet you’ll find some outlier in there which will also be rare if you just look far enough.
I believe it will be very hard to really distinguish between real and chance cycles. I would start with a textbook example which cycles without error. Hill climb your probability system to increasingly better results (fake/real cycles). Use all information you can extract about cycles, positions, distances, symbols in between. A cycle which is real will probably have a better spread throughout the cipher since that is the nature of cyclic homophonic, etc. Would like to help with a system of my own but I’m preoccupied with working on my solver, if this theory pans out we need a solver which can do higher multiplicity than the ones available.
Keep up the good job andalso take it easy! ![]()
Hey guys, thanks for working on this.
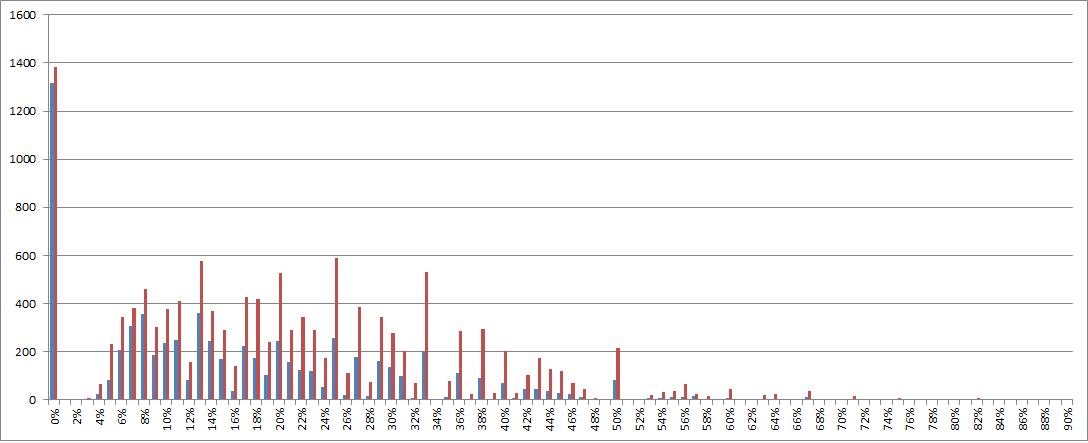
I was looking back through all of my spreadsheets and found one randomization that I did for 3 symbol cycles and forgot about. It probably took me a day to do it.
Here is a simple idea about how to tackle this:
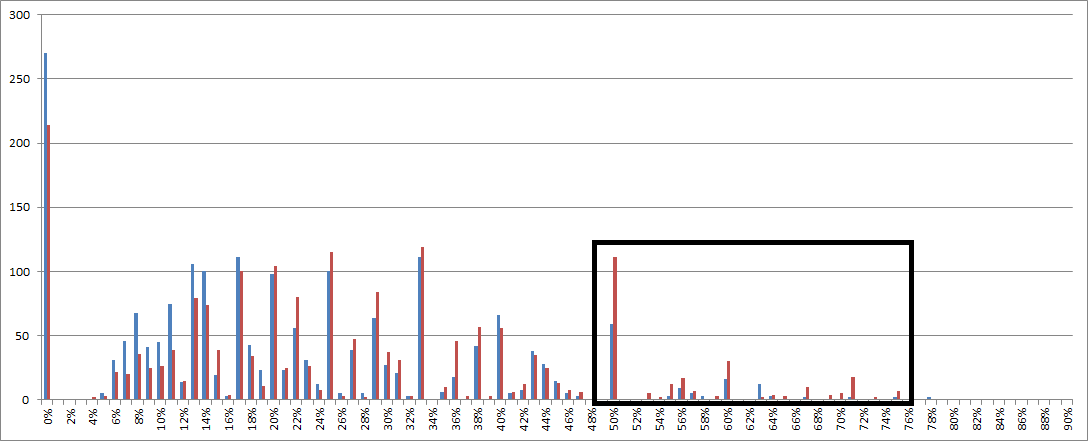
Check out the distribution below. The Zodiac 340 scores, totaled by percentage, are in red. The ONE randomization score, totaled by percentage, are in blue.
Now that doranchak has identified all of the cycles, we need to find the probability for each cycle that Zodiac made the cycle, and then attack the ones with the highest confidences.
See the 50% mark, for example. There are 215 L-3 cycles in the Zodiac 340 that score 50%. There are 84 L-3 cycles (you would have to see the spreadsheet) in the Randomized 340 that score 50%. The probability that any particular 50% L-3 cycle in the Zodiac 340 is author made should be: (215-84)/215=61%.
Now to the 71% mark. There are 16 L-3 cycles in the Zodiac 340 that score 71%. There are only 3 L-3 cycles (you would have to see the spreadsheet) in the Randomized 340 that score 71%. The probability that any particular 71% L-3 cycle in the Zodiac 340 is author made should be: (16-3)/16=81%.
What really needs to be done is to generate only 30 randomizations to find good statistical data to work with. Then find the mean (and possibly the standard deviations) for each score percentage. Make a distribution graph and compare to the Z340 graph. Do a separate graph for L-2, L-3, etc.
Then, with our list of cycles, we can work with the highest confidence cycles to try to solve the Z340.
The wildcard hypothesis may fizzle out, I don’t know. But either way, we will have a list of cycles to work with and know for a fact for any particular cycle how probable it is that Zodiac made it. The cycles need to be sorted into different groups to work with.
I don’t know what you guys are talking about sometimes, and if you find a more efficient way to do this, then that is fine. I loved doranchak’s random shuffle idea because it was a very efficient test to find whether we should move forward.
My humble suggestion is to keep it simple so that other people (not just me) can work with the data on it if necessary. So that people can see that Zodiac DID use cycles, see how the cycles are sorted into confidence groups, and see what cycles to attack. It is possible that the message could reveal itself very quickly with your computer programs.
Smokie
Another thought: All of the symbols in each high confidence cycle could be replaced with only one new symbol that represents that cycle. That may make solving easier.
What really needs to be done is to generate only 30 randomizations to find good statistical data to work with. Then find the mean (and possibly the standard deviations) for each score percentage. Make a distribution graph and compare to the Z340 graph. Do a separate graph for L-2, L-3, etc.
You may not have seen this 100 randomised 340’s. I posted it earlier. If you need anything else let me know.