Experiment 1 J-ST
Yours is different from the 340 when I sort the two symbol comparisons by score. It’s just that yours lines up so perfectly and it is easy to see what the cycles are:
Z340 Scores 60% and up:
See what I mean about patterns? That’s part of why I was so convinced that he used cycles.
S.T.
Experiment 2 J-ST
That took about an hour. You wanted me to find Symbols 16, 17, 27 and 32.
Note that if two symbols have a cyclical relationship, then their count should be roughly the same. All of the symbols with a count of 7, for example, would have a good chance of being cyclically related to each other and also the symbols with a count of 5 and 6 because a cycle can get cut off at the end of the message.
Symbol 16 only had two scores above 50%, which was a red flag because the shift in the two symbol distribution comparison is at 50%.
I worked my way up from the bottom of the table, and stopped at 16. I think that’s what you wanted me to find.
Next time just a grid of numbers in ZKDecrypto format.
S.T.
P.S. I should also work the 340 again on the new spreadsheet in the near future.
I don’t know if this helps, but here is some more evidence that Z340 contains intentional cycles.
First, I updated my cycle search so it only counts sequences that are contiguous. For example, ABABAB will count as 3 repetitions but ABAAAB will only count as 1.
This spreadsheet shows all the cycles found, ordered by a probability score: https://docs.google.com/spreadsheets/d/ … sp=sharing
There are 3 ciphers in there: Z340, Z408 and R340. R340 is a shuffled Z340. The tabs at the bottom let you pick different cycle lengths and ciphers.
The score that I’m using is a simple relative probability, done by looking at symbol counts. For example, consider a cycle ABABAB. Let "a" be the number of times "A" appears in the cipher, and "b" be the number of times "B" appears. Then, the probability of selecting A and B is (a/340)*(b/340). Since ABABAB has 3 contiguous repetitions, the full probability becomes (a/340)*(b/340)*(a/340)*(b/340)*(a/340)*(b/340). The thinking behind this approach is that there may be another cycle, CDCDCD. They have the same length, but what if there are more C’s and D’s in the cipher text than A’s and B’s? Then, the probability score will rank ABABAB above CDCDCD.
Another column of the spreadsheet is "Coverage", which I think is equivalent to smokie’s percentage score.
I plotted the sorted probabilities for L=2 for Z340, R340, and Z408:

Y axis is the probability score, and X axis is just the data point number. You’ll see that at the left, all 3 ciphers have cycles with very low probabilities. But as you go to the right, you’ll see that the probabilities go up, first for the shuffled cipher (r340), then for z340, then for z408.
So, the shuffled cipher (r340) seems to have far more cycles with greater probabilities than the cycles of the original cipher (z340). I still need to compare the distributions of cycle probabilities with more shuffled ciphers, but it sure does seem like z340 has intentional cycles in it.
Thank you very much for the spreadsheets.
I am sure that we will be able to learn a great deal about the Z340 by examining the information.
S.T.
Thanks for the information on probabilities doranchak.
Well done smokie, both ciphers are correctly identified. I wasn’t sure how the interactions between cycles would play out.
I now introduced various degrees of randomness to the majority of the cycles. Though it could still be considered cyclic, but probably on the weaker side. I’m wondering if you could identify any 1:1 substitutes here. Given the randomness here and there it may be very hard. Would also like to know how you well you think this cipher compares to the 340 and if you could give reason to suspect any of them to be wildcards. I’m interested to know if the introduced randomness + 1:1 substitutes could simulate the wildcard hypothesis.
Good luck ![]()
----------------- Nummeric cipher for ZKDecrypto: ----------------- 1 2 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 17 19 20 21 22 23 4 24 25 26 27 28 29 30 31 32 33 11 18 34 29 11 12 13 35 36 10 37 10 24 21 33 2 15 38 39 40 41 21 42 9 43 18 44 31 29 26 32 45 34 46 47 28 44 3 36 48 20 40 49 10 50 10 7 20 15 34 21 51 46 42 11 33 30 4 1 29 6 27 16 8 45 32 33 25 19 36 31 11 44 43 23 34 35 39 5 12 18 52 20 9 32 53 54 2 34 38 42 55 14 46 43 56 57 48 2 41 24 3 39 48 13 47 58 52 5 17 11 15 27 33 18 44 22 28 6 36 34 31 26 10 57 40 18 44 17 30 29 1 59 40 32 16 60 49 10 19 23 22 7 21 36 12 31 11 47 61 31 18 44 24 13 28 27 25 35 36 42 49 18 4 5 46 9 33 56 42 11 38 36 17 29 36 34 7 32 54 42 49 15 12 49 62 11 53 43 18 20 59 7 48 51 41 16 48 1 3 29 58 33 6 19 39 48 49 10 8 25 42 23 4 46 42 5 21 36 22 26 36 37 10 56 24 28 60 35 32 38 39 5 11 33 55 34 49 18 14 41 33 7 43 2 31 28 27 18 34 32 13 3 4 10 11 48 36 10 21 25 5 11 6 2 42 29 21 17 19 39 47 15 31 5 28 44 30 40 57 56 34 44 59 2 51 62 1 18 44 63 22 57 52 11 4 22 53 8 28 44 23 36 12
Jarvle: This is an excellent project and may take a little time. I will try to flush out the high count symbols that do not have strong cyclical relationships with other symbols and compare to Z340. The project is also making me think about my prior attempt at grouping the symbols into categories and how to do that in different ways, including some type of graphic. It’s all trial and error, which I enjoy.
doranchak: Your spreadsheets are excellent and what I have been hoping for. I have been thinking about methods for scoring the cycles, and have some comments.
What I was trying to do with my scoring system was reward both total length and purity for purposes of flushing out the most likely candidates for Zodiac made cycles. For instance, ABABABAB, eight symbols in count, would have the same score as ABCDABCD, a 75% because six of the eight symbols in each (not including the first and last symbol) have a symbol to both the left and right of it that are the symbol that it should be if in the cycle. The logic being that short cycles such as ABAB would only score 50% and therefore not be of much use to me, since those could easily be random. A cycle ABABAB*B would have a score of 5/8=63%, which takes into account the missing symbol and makes the cycle rank lower on my sorted list of scored cycles; I would prefer to work with long perfect cycles if possible.
However… this is an artificial way to score the cycles and may not show their relative strengths; I have no idea if ABABABAB is any more or less likely to occur at random than ABCDABCD.
I grasp the concept of your scoring system:
The score that I’m using is a simple relative probability, done by looking at symbol counts. For example, consider a cycle ABABAB. Let "a" be the number of times "A" appears in the cipher, and "b" be the number of times "B" appears. Then, the probability of selecting A and B is (a/340)*(b/340). Since ABABAB has 3 contiguous repetitions, the full probability becomes (a/340)*(b/340)*(a/340)*(b/340)*(a/340)*(b/340). The thinking behind this approach is that there may be another cycle, CDCDCD. They have the same length, but what if there are more C’s and D’s in the cipher text than A’s and B’s? Then, the probability score will rank ABABAB above CDCDCD.
Let’s say that A and B each appear three times in the message with ABABAB. I get 4.71904E-13. Now if C and D each appear four times with CDCDCDCD, I get 3.66985E-16. Does ABABAB score higher or lower than CDCDCDCD? CDCDCDCD would rank higher, even though the actual score number is lower, correct?
I am not sure that only ranking the cycle strings that have two contiguous perfect cycles will show all of the most likely candidates for Zodiac made. For instance, ABA*ABABABABAB would not show up at the top of your spreadsheet, but it would score higher with other methods.
I have another idea that takes from your shuffle idea.
Let’s say we identify a handful of common patterns and find the mean number of random shuffles out of 30 trials to get that pattern to appear. Then we would might have a more relevant way to measure how the cycles compare to each other.
ABABABC 10 random shuffles
ABCDABCD 100 random shuffles
ABCABCABC 200 random shuffles
Something like that. Real simple. A little table of common patterns to give us some perspective.
Memories in my old brain from statistics class tell me that statisticians often take 30 random samples from a population to compare with a population under study. But that example is not exactly like what we are dealing with here. Just thinking that more than 30 shuffles may not change the results all that much. Just thinking that this might be the most practical approach and eliminates trying to make any artificial scoring system that may not be the best one.
Another thought: I enjoy working with the two of you. I just hope that we are working smart instead of working hard. You guys know how to solve these types of problems with computers, and have powerful programs. I am wondering if either of you can think of ways to speed up finding a solution with what we have already learned or could observe from looking over the top scoring cycles that doranchak has identified.
Thanks, and I will work on Experiment 3 J-ST and think of another way to categorize the symbol groups with my currently artificial but not necessarily most relevant scoring system.
S.T.
Jarvle: This is an excellent project and may take a little time. I will try to flush out the high count symbols that do not have strong cyclical relationships with other symbols and compare to Z340. The project is also making me think about my prior attempt at grouping the symbols into categories and how to do that in different ways, including some type of graphic. It’s all trial and error, which I enjoy.
I also believe in trial and error, we humans basicly do hill climb our problems to a solution. That’s why (most of us) are not calculators. Here are 100 randomised/shuffled 340’s in numbers format each time renumbered by appearance: download from google.
Another thought: I enjoy working with the two of you. I just hope that we are working smart instead of working hard. You guys know how to solve these types of problems with computers, and have powerful programs. I am wondering if either of you can think of ways to speed up finding a solution with what we have already learned or could observe from looking over the top scoring cycles that doranchak has identified.
I have an interesting idea. You guys have been looking at probabilities of individual cycles (well mostly). I propose looking at the probabilities of a full distribution of cycles with the goal to reduce the number of symbols from 63 to somewhere 20-26. A hill climber that sorts out the number of letters and the cycle per letter.
Key1: number of letters.
Key2: symbols (part of cycle) per letter.
Operations: a) increment/decrement letter, b) swap symbols.
Measurement system has to be such that the total score of the actual cycles in the cipher is the global optimum.
There may be some problems with this system, it may or not have multiplicity issues. If some transposition was applied after or during encoding of the 340 then it will fail. If the wildcard hypothesis is true then it may need adjustement. It may have problems when randomisation of the cycles is actual.
Doranchak do you think it is possible to come up with such a measurement system? If you think it’s possible and you see some merit in this approach by all means feel free to try it. If you think it’s unprobable or don’t have the time to try this approach could you point me in the right direction? Thank you.
What I was trying to do with my scoring system was reward both total length and purity for purposes of flushing out the most likely candidates for Zodiac made cycles. For instance, ABABABAB, eight symbols in count, would have the same score as ABCDABCD, a 75% because six of the eight symbols in each (not including the first and last symbol) have a symbol to both the left and right of it that are the symbol that it should be if in the cycle. The logic being that short cycles such as ABAB would only score 50% and therefore not be of much use to me, since those could easily be random. A cycle ABABAB*B would have a score of 5/8=63%, which takes into account the missing symbol and makes the cycle rank lower on my sorted list of scored cycles; I would prefer to work with long perfect cycles if possible.
However… this is an artificial way to score the cycles and may not show their relative strengths; I have no idea if ABABABAB is any more or less likely to occur at random than ABCDABCD.
We can compute that directly from a very simple example, and then build from it. Let’s consider a cipher with the alphabet {A,B,C,D}. To support the appearance of the cycles ABABABAB and ABCDABCD, the minimum frequency counts for the alphabet have to be: {4,4,2,2}. So, to use all those symbols, let’s start with a cipher length of 4+4+2+2 = 12.
Since our "mini cipher" has length 12, and ABABABAB is of length 8, the cycle ABABABAB can appear in 5 different spots:
ABABABABAB****
*ABABABABAB***
**ABABABABAB**
***ABABABABAB*
****ABABABABAB
Since we’ve used up all the A’s and B’s in those 5 possibilities, the remaining 4 spots are filled with C’s and D’s. There are 6 ways for those to appear: CCDD, CDCD, CDDC, DCCD, DCDC, and DDCC. That means that ABABABAB appears in 5*6 = 30 of all the possible cipher configurations.
By the same logic, the cycle BABABABA also appears in 30 of all possible cipher configurations. CDCDCDCD cannot be formed because we don’t have enough Cs and Ds.
So, there are 2*30 = 60 possible cipher configurations that would contain ABABABAB or BABABABA.
Now let’s look at ABCDABCD. It, too, can appear in 5 different spots. Then, the available remaining symbols are 2 As, 2 Bs. With the same reasoning as above, there are 6 ways for the remaining As and Bs to appear, so ABCDABCD appears in 30 of all possible cipher configurations.
But we would also notice cycles such as DCBADCBA, right? So we need to count those as well. But now we realize there are many more possibilities (24 of them):
ABCDABCD, ABDCABDC, ACBDACBD, ACDBACDB, ADBCADBC, ADCBADCB, BACDBACD, BADCBADC, BCADBCAD, BCDABCDA, BDACBDAC, BDCABDCA, CABDCABD, CADBCADB, CBADCBAD, CBDACBDA, CDABCDAB, CDBACDBA, DABCDABC, DACBDACB, DBACDBAC, DBCADBCA, DCABDCAB, DCBADCBA
So, there are 24*30 = 720 possible cipher configurations that would contain this kind of cycle pattern. Note that 720/60 = 12. There are 12 times as many patterns of the form ABCDABCD as patterns of the form ABABABAB.
That means ABABABAB is much less likely to occur by chance than ABCDABCD, provided that you are considering all the other forms of the patterns.
Does this make sense?
To verify my analysis, I wrote a quick program to generate all the unique cipher texts from the alphabet described above. Here are the outputs: http://zodiackillerciphers.com/mini-cipher.txt
There are 207,900 unique cipher texts from that alphabet. The probability of ABABABAB or BABABABA occurring by chance is 60/207900 = 0.03%. The probability of ABCDABCD (or one of the other 23 pattern types like that) occurring by chance is 720/207900 = 0.35%.
Of course, these probabilities change as we adjust the frequencies of the symbols in the cipher alphabet. I think it would be a worthy exercise to compute the exact probabilities based on the cipher length and symbol frequencies, for any cipher text. Then it will give you an exact way to compare different cycles to each other.
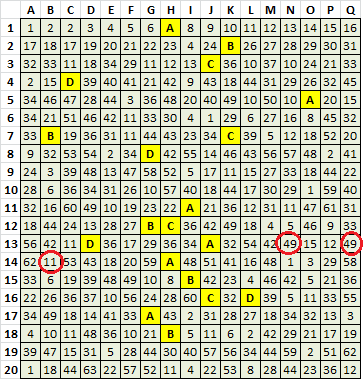
Wow, this is getting really intense. Jarlve, I have been working on Experiment 3 J-ST.
I. Search for 1:1 or wildcards
A. First, I checked all symbols with a count of 5 or more and which had few scores above 50%. Not an exact science, but looked there first. Strong candidates for 1:1 or wildcard are 10 and 2. Symbol 2, however does have some cycling with 28 which is either random or caused by multiple deletions or substitutions in the cycle.
Other possible candidates are 11, 36, 21, 29, 48 and 49. However, all cycle with other symbols.
Marginal candidates are 17 and 49, which also cycle with other symbols.
B. Only one symbol with a count of 6 or more had perfect cycles, but there are many symbols with counts of 6 or more that score high. This suggests cycles that include symbols with a count of 6 or higher, but have missing symbols.
There are many perfect cycles as well, especially with symbols that have a count of 5 or less. The distribution below shows this. Green is Experiment 3 J-ST and red is Z340. There are more higher scoring or perfect cycles than Z340, but it is similar.
Because there are definitely a lot of cycles, this supports the theory that 2 is a 1:1 or wildcard. Symbol 2 is high count, but if 2 was in a cycle, it would not be in a side by side condition as seen in row 1. If 22 was a wildcard, however, then 22 would have to start a cycle as a wildcard because 22 sits next to 1, and 1 is in a cycle with 23, 35, 38, and 41.
II. Examples of High Scoring Cycles with Missing Symbols
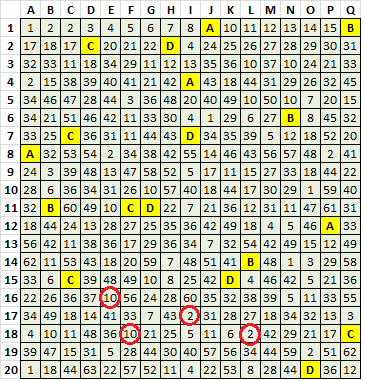
A. Symbols 32 and 33 are probably in an intentional cyclical relationship, but have missing symbols:
32 33 * 33 32 33 32 33 32 33 32 33 32 33 32 33 * 33 32
Symbol 32 does have some cycling with 5, 11, 39 and 43, but if any of those are added to the 32 33 cycle, I don’t see much of a pattern.
In the message below, I show that some of the suggested 1:1 substitutes are there where the missing 32 should be found. The A represents 32 and the B represents 33. A=32 and B=33.
B. Symbols 7, 25, 35 and 38 are probably in an intentional cycle, but have three contiguous missing symbols that could be replaced with wildcards:
7 25 35 38 7 25 35 38 7 25 35 38 7 * * * 7 25 35 38 7 25
A=7, B=25, C=35 and D=38
I am really curious to know if you did this on purpose, or perhaps one of the symbols falls into the cycle by chance. Or is all of this a coincidence?
C. Symbols 9, 16, 19 and 23 are probably in an intentional cycle, but have two contiguous missing symbols that could be replaced with wildcards:
9 16 19 23 9 16 19 23 9 16 19 23 9 16 19 23 * * 19 23
How are those for examples? Did you create any of those cycles? I could look for more but am curious if I am finding random cycles or not.
S.T.
I have a possibly naive question. Is is possible to take a handful of the highest scoring cycles, use frequency analysis to determine their probable plaintext, and plug those into your computer programs to see what happens. Can we do that now, or is that premature?
Thanks for your in-depth analysis smokie,
You did catch on to some things here and there but it shows that some randomness can go a long way. I came up with the idea of hiding the 1:1 substitutes by adding some extra randomness to a few cycles that had similar counts. And it seems to have worked, you could see this as a worst case scenario. I guess that 1:1 substitutes are not entirely unplausable for the 340.
Now we have to create an actual wildcard cipher by hand. I will do this saturday or sunday. After that I have something else which I would like you to look at.
The cipher your analysed:
p44.txt ----------------- Symbols: 63 Characters: 340 Multiplicity: 0.1852941 Sum of non-repeats: 4175 Index of coincidence: 0.0172479 ----------------- Symbols numbered by order of appearance: ----------------- 1 = k (c=5) 2 = u (c=8) 3 = o (c=5) 4 = , (c=7) 5 = e (c=8) 6 = r (c=5) 7 = 1 (c=6) 8 = F (c=4) 9 = . (c=4) 10 = 7 (c=11) 11 = 3 (c=13) 12 = [ (c=6) 13 = g (c=5) 14 = % (c=3) 15 = t (c=6) 16 = V (c=4) 17 = ^ (c=6) 18 = J (c=12) 19 = R (c=5) 20 = ` (c=5) 21 = v (c=8) 22 = _ (c=6) 23 = > (c=5) 24 = w (c=5) 25 = ! (c=5) 26 = < (c=4) 27 = (c=5) 28 = O (c=8) 29 = X (c=8) 30 = p (c=4) 31 = P (c=8) 32 = @ (c=8) 33 = E (c=9) 34 = T (c=10) 35 = ' (c=4) 36 = N (c=12) 37 = 6 (c=2) 38 = G (c=4) 39 = I (c=6) 40 = - (c=5) 41 = ( (c=4) 42 = h (c=9) 43 = + (c=5) 44 = z (c=10) 45 = Q (c=2) 46 = L (c=5) 47 = : (c=4) 48 = i (c=7) 49 = ; (c=7) 50 = Z (c=1) 51 = U (c=3) 52 = l (c=3) 53 = y (c=3) 54 = q (c=2) 55 = d (c=2) 56 = n (c=4) 57 = # (c=4) 58 = C (c=2) 59 = / (c=3) 60 = Y (c=2) 61 = = (c=1) 62 = ? (c=2) 63 = m (c=1) ----------------- Symbolic cipher: ----------------- kuuo,er1F.73[g%tV ^J^R`v_>,w!<OXpP @E3JTX3[g'N767wvE utGI-(vh.+JzPX<@Q TL:OzoNi`-;7Z71`t TvULh3Ep,kXrVFQ@ E!RNP3z+>T'Ie[Jl` .@yquTGhd%L+n#iu( woIig:Cle^3tEJz_ OrNTP<7#-Jz^pXk/- @VY;7R>_1vN[P3:=P JzwgO!'Nh;J,eL.E nh3GN^XNT1@qh;t[; ?3y+J`/1iU(VikoXC ErRIi;7F!h>,LhevN _<N67nwOY'@GIe3Ed T;J%(E1+uPOJT@go ,73iN7v!e3ruhXv^R I:tPeOzp-#nTz/uU? kJzm_#l3,_yFOz>N[ ----------------- Nummeric cipher: ----------------- 1,2,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 17,18,17,19,20,21,22,23,4,24,25,26,27,28,29,30,31 32,33,11,18,34,29,11,12,13,35,36,10,37,10,24,21,33 2,15,38,39,40,41,21,42,9,43,18,44,31,29,26,32,45 34,46,47,28,44,3,36,48,20,40,49,10,50,10,7,20,15 34,21,51,46,42,11,33,30,4,1,29,6,27,16,8,45,32 33,25,19,36,31,11,44,43,23,34,35,39,5,12,18,52,20 9,32,53,54,2,34,38,42,55,14,46,43,56,57,48,2,41 24,3,39,48,13,47,58,52,5,17,11,15,27,33,18,44,22 28,6,36,34,31,26,10,57,40,18,44,17,30,29,1,59,40 32,16,60,49,10,19,23,22,7,21,36,12,31,11,47,61,31 18,44,24,13,28,27,25,35,36,42,49,18,4,5,46,9,33 56,42,11,38,36,17,29,36,34,7,32,54,42,49,15,12,49 62,11,53,43,18,20,59,7,48,51,41,16,48,1,3,29,58 33,6,19,39,48,49,10,8,25,42,23,4,46,42,5,21,36 22,26,36,37,10,56,24,28,60,35,32,38,39,5,11,33,55 34,49,18,14,41,33,7,43,2,31,28,27,18,34,32,13,3 4,10,11,48,36,10,21,25,5,11,6,2,42,29,21,17,19 39,47,15,31,5,28,44,30,40,57,56,34,44,59,2,51,62 1,18,44,63,22,57,52,11,4,22,53,8,28,44,23,36,12 ----------------- Nummeric cipher for ZKDecrypto: ----------------- 1 2 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 17 19 20 21 22 23 4 24 25 26 27 28 29 30 31 32 33 11 18 34 29 11 12 13 35 36 10 37 10 24 21 33 2 15 38 39 40 41 21 42 9 43 18 44 31 29 26 32 45 34 46 47 28 44 3 36 48 20 40 49 10 50 10 7 20 15 34 21 51 46 42 11 33 30 4 1 29 6 27 16 8 45 32 33 25 19 36 31 11 44 43 23 34 35 39 5 12 18 52 20 9 32 53 54 2 34 38 42 55 14 46 43 56 57 48 2 41 24 3 39 48 13 47 58 52 5 17 11 15 27 33 18 44 22 28 6 36 34 31 26 10 57 40 18 44 17 30 29 1 59 40 32 16 60 49 10 19 23 22 7 21 36 12 31 11 47 61 31 18 44 24 13 28 27 25 35 36 42 49 18 4 5 46 9 33 56 42 11 38 36 17 29 36 34 7 32 54 42 49 15 12 49 62 11 53 43 18 20 59 7 48 51 41 16 48 1 3 29 58 33 6 19 39 48 49 10 8 25 42 23 4 46 42 5 21 36 22 26 36 37 10 56 24 28 60 35 32 38 39 5 11 33 55 34 49 18 14 41 33 7 43 2 31 28 27 18 34 32 13 3 4 10 11 48 36 10 21 25 5 11 6 2 42 29 21 17 19 39 47 15 31 5 28 44 30 40 57 56 34 44 59 2 51 62 1 18 44 63 22 57 52 11 4 22 53 8 28 44 23 36 12 ----------------- Symbolic cycles: ----------------- Old symbol: a, homophone(s): kF%+:-U (kF%-+:-UkF+%+:-k-:+UkF%+:-UkF) Old symbol: l, homophone(s): uln# (uuulun#ul#nnuu#nu#l) Old symbol: t, homophone(s): orR>'G( (orR>'G(orR>'G(orR>'G(orR>'G(orR>) Old symbol: h, homophone(s): ,NI (,,NIN,NIINNN,NNI,NNI,NI,N) Old symbol: e, homophone(s): Ti7he (e7T77hTi77ThTeThiieT77hehThiii7hhe7eTT7i7eheT) Old symbol: r, homophone(s): 1!L; (1!L;1L!L;1!;L1;;1;!L;1!) Old symbol: c, homophone(s): .<p (.<p.<p.<p.<p) Old symbol: s, homophone(s): 3X (3X3X3X3X33X33X3X333X3) Old symbol: o, homophone(s): [w@ ([w@[w@@[@w@[w@[w@@[) Old symbol: f, homophone(s): gtV (gtVgttVgtVgtVgt) Old symbol: i, homophone(s): ^_P (^^_PPP^_P^_PP^_P^P__) Old symbol: n, homophone(s): JO (JOJJOJJOJJOJJOJOJOJO) Old symbol: y, homophone(s): ` (`````) Old symbol: w, homophone(s): v (vvvvvvvv) Old symbol: u, homophone(s): E (EEEEEEEEE) Old symbol: b, homophone(s): 6C (6CC6) Old symbol: d, homophone(s): z (zzzzzzzzzz) Old symbol: v, homophone(s): QZ (QZQ) Old symbol: m, homophone(s): y? (y?y?y) Old symbol: p, homophone(s): qd (qdqd) Old symbol: g, homophone(s): /Y (/Y/Y/) Old symbol: k, homophone(s): =m (=m) ----------------- Nummeric cycles: ----------------- Old symbol: a, homophone(s): 1,8,14,43,47,40,51 (1,8,14,40,43,47,40,51,1,8,43,14,43,47,40,1,40,47,43,51,1,8,14,43,47,40,51,1,8) Old symbol: l, homophone(s): 2,52,56,57 (2,2,2,52,2,56,57,2,52,57,56,56,2,2,57,56,2,57,52) Old symbol: t, homophone(s): 3,6,19,23,35,38,41 (3,6,19,23,35,38,41,3,6,19,23,35,38,41,3,6,19,23,35,38,41,3,6,19,23,35,38,41,3,6,19,23) Old symbol: h, homophone(s): 4,36,39 (4,4,36,39,36,4,36,39,39,36,36,36,4,36,36,39,4,36,36,39,4,36,39,4,36) Old symbol: e, homophone(s): 34,48,10,42,5 (5,10,34,10,10,42,34,48,10,10,34,42,34,5,34,42,48,48,5,34,10,10,42,5,42,34,42,48,48,48,10,42,42,5,10,5,34,34,10,48,10,5,42,5,34) Old symbol: r, homophone(s): 7,25,46,49 (7,25,46,49,7,46,25,46,49,7,25,49,46,7,49,49,7,49,25,46,49,7,25) Old symbol: c, homophone(s): 9,26,30 (9,26,30,9,26,30,9,26,30,9,26,30) Old symbol: s, homophone(s): 11,29 (11,29,11,29,11,29,11,29,11,11,29,11,11,29,11,29,11,11,11,29,11) Old symbol: o, homophone(s): 12,24,27,32 (12,24,27,32,12,24,32,27,32,12,32,24,27,32,12,24,27,32,12,24,32,27,32,12) Old symbol: f, homophone(s): 13,15,16 (13,15,16,13,15,15,16,13,15,16,13,15,16,13,15) Old symbol: i, homophone(s): 17,22,31 (17,17,22,31,31,31,17,22,31,17,22,31,31,17,22,31,17,31,22,22) Old symbol: n, homophone(s): 18,28 (18,28,18,18,28,18,18,28,18,18,28,18,18,28,18,28,18,28,18,28) Old symbol: y, homophone(s): 20 (20,20,20,20,20) Old symbol: w, homophone(s): 21 (21,21,21,21,21,21,21,21) Old symbol: u, homophone(s): 33 (33,33,33,33,33,33,33,33,33) Old symbol: b, homophone(s): 37,58 (37,58,58,37) Old symbol: d, homophone(s): 44 (44,44,44,44,44,44,44,44,44,44) Old symbol: v, homophone(s): 45,50 (45,50,45) Old symbol: m, homophone(s): 53,62 (53,62,53,62,53) Old symbol: p, homophone(s): 54,55 (54,55,54,55) Old symbol: g, homophone(s): 59,60 (59,60,59,60,59) Old symbol: k, homophone(s): 61,63 (61,63)
I have a possibly naive question. Is is possible to take a handful of the highest scoring cycles, use frequency analysis to determine their probable plaintext, and plug those into your computer programs to see what happens. Can we do that now, or is that premature?
It’s an idea similar to what I was suggesting. To come down from 63 symbols to 20-26 letters. Scroll back to my previous post to read it. There’s a catch, maybe you could help me with it. I’ll explain it more thoroughly. A handful of high scoring cycles do not fill up an entire cipher, and they may be wrong. Too many variations.
We need a measurement system that is such that the total score of all cycles in the cipher is the global optimum. The global optimum is the highest score available when you consider all other possible cycle distributions over the letters. Why? Because otherwise the hill climbing algorithm will not get it, it climbs to the highest score and not to some point in the middle.
In the program there are some keys. Key 1 is the number of letters. We don’t know how many letters are used in the 340 so we gradually increment key 1 (letters=20,letters=21,letters=22,…) to see what amount of letters gives the best score.
There is also a key 2 which holds a cycle for each letter in key 1. The cycles are at first distributed randomly and then are tried to improve upon by making changes. The next 4 following steps describe the hill climbing algorithm in such a program.
1) Make a random change to key 2.
2) Score all cycles individually (of key 2) with the measurement system, add them together and remember this value as the score.
3a) If the score is higher than the previous score then keep the change.
3b) If the score is lower than the previous score then revert the random change.
4) Go back to step 1.
I believe this variation is called a stochastic hill climber and it’s what I use in AZdecrypt with some extras thrown in. So all I need to get this to work is a measurement system as I described. Your ideas are welcome, and if you have an entirely different idea I would certainly like to consider it.
Also, we know that from solvers like ZKDecrypto (which use the hill climbing approach) that a full grid english solution in a left-to-right, top-to-bottom manner is not available for the 340. That’s something for which you can take my word on. Something else is going on. Interruptions would certainly do the trick – such as your wildcard theory – given that they are plenty. In this thread we were able to recover the plaintext of the 408 with a wildcard simulation using 24 symbols. pi suggested it was easy but given that it only scored 32000 it was a borderline solve.
If wildcards are actual in the 340 and the wildcard symbols are correct (there are no more or less) I may be able to extract a partial solve from the 340 this weekend with my own solver using the consonant/vowel technique I have been talking about earlier in this thread.
Jarlve:
I understand about making small changes and trying over and over until getting higher scores.
I am surprised about Symbols 32 and 33. I thought for sure that you made that cycle because it was so long. But 33 was a 1:1 and 32 was included in a randomized cycle. The result was an (improbable?) cycle relationship. 32 33 33 32 33 32 33 32 33 32 33 32 33 32 33 33 32.
I will be waiting in the starting blocks for any new coded message.
doranchak: I read your explanation, and grasp the basic concept. I have some thoughts, however. When I manually try to find cycles in the message, I could find ABCDABCD. However, because of the way that I have my ciphertext numbered, the first cycle, ABCD will always appear no matter what. It’s the probability of getting another, second ABCD is what I wonder about. In your example, you give some possibilities such as ABDCABDC. But that cannot occur the way that, at least I, have the ciphertext numbered. If you take into account the fact that B could never come before A in the first cycle, does your analysis change?
My comments about your requiring two contiguous cycles for scoring was misplaced; I wasn’t thinking straight and had been looking at L-7.
S.T.
doranchak: I read your explanation, and grasp the basic concept. I have some thoughts, however. When I manually try to find cycles in the message, I could find ABCDABCD. However, because of the way that I have my ciphertext numbered, the first cycle, ABCD will always appear no matter what. It’s the probability of getting another, second ABCD is what I wonder about. In your example, you give some possibilities such as ABDCABDC. But that cannot occur the way that, at least I, have the ciphertext numbered. If you take into account the fact that B could never come before A in the first cycle, does your analysis change?
That makes sense. So, looking back at my example, if we apply your symbol numbering scheme to the 207,900 possible symbolic cipher texts based on my sample alphabet, then there are only 51,975 possible cipher texts (exactly one forth of the original symbolic cipher texts): http://zodiackillerciphers.com/mini-cip … erical.txt
This is because each numerical representation can stand for exactly 4 of the original cipher texts, since we are mapping to symbol order instead of a strictly to specific symbols.
I think this means the probabilities do not change, since if you have a numerical cipher such as 0 1 2 3 0 1 2 3 4 5 4 5, it can represent 4 different original symbol ciphers, so we still have to count all 4 of the originals.
Here are all the 144 distinct ways the L=4 cycles can repeat in the numerical version: http://zodiackillerciphers.com/mini-cip … les-L4.txt
Here are all the 15 distinct ways the L=4 cycles can repeat in the numerical version: http://zodiackillerciphers.com/mini-cip … les-L2.txt
So you can see the L=4 cycles are still more likely to occur by chance than the L=2 cycles. I did notice, though, that 144 times 4 = 576, but I previously calculated that 720 (not 576) L=4 cycles should appear among all the possible sample ciphertexts. Not sure if I made a small mistake somewhere (maybe I overcounted in the symbol version, or undercounted in the numerical version).
I’m working on pushing a better solve out of the 408 wildcard simulation, the results seem to have improved a bit (judging from example 1 in contrast to the other example I posted a few pages back). When example 1 is the dominant scheme that comes out of the solver I will move back to the 340. The problem currently is that example 2 scores higher and therefore is the dominant scheme.
Example 1:
ilittallingpeople auceitionbrunhusa idrourfunshaillin gwlerdistahorsete neusraintherostag grtudeneralofallt otilloodthaggiaan ehersthrillingspe rndicaenmetssuesg ettingyoursontohi shegalthdntparthi sietherwhateiwill messmounspareanen tallthrihadtilywl lmorerycleasoiwil osgaasoursaremana udyouwilltu
Example 2:
ngessyhgarlgeight errendermisrhmrly alsoftwranninther ligasealotmuchedt herosenmonesinhil ltorearesehowitho usethriedbyllactm entsnobcnthealoge thearterstonofall edonalforcouhsrme nbelygonemdgecoma nneobatintheainth stoosofrlgicayhea heggobtancesngwit hsistsfrtecorning onlycoursliststhe reforingtof