I have an interesting idea. You guys have been looking at probabilities of individual cycles (well mostly). I propose looking at the probabilities of a full distribution of cycles with the goal to reduce the number of symbols from 63 to somewhere 20-26. A hill climber that sorts out the number of letters and the cycle per letter.
Key1: number of letters.
Key2: symbols (part of cycle) per letter.
Operations: a) increment/decrement letter, b) swap symbols.
Measurement system has to be such that the total score of the actual cycles in the cipher is the global optimum.There may be some problems with this system, it may or not have multiplicity issues. If some transposition was applied after or during encoding of the 340 then it will fail. If the wildcard hypothesis is true then it may need adjustement. It may have problems when randomisation of the cycles is actual.
Doranchak do you think it is possible to come up with such a measurement system? If you think it’s possible and you see some merit in this approach by all means feel free to try it. If you think it’s unprobable or don’t have the time to try this approach could you point me in the right direction? Thank you.
I think this kind of approach might be really effective. It reminds me of King and Bahler’s method – have you seen it? http://www.oranchak.com/king-homophonic-ciphers.pdf I think their method exploits qualities that arise from applying numerical numbering of cipher symbols, and it avoids frequency analysis, statistics, and backtracking. But I think it is sensitive to randomness in the cycles, so it will fail to detect some strong cycles if they are sufficiently imperfect.
I do suspect that the total score of the actual cycles in the cipher will not be the global optimum, though. This would have to be tested.
Some general thoughts. I really think that we are on the right track. I like the idea of working with the cycles as a group, and the symbols as a group to try to identify characteristics about each so that we can break them down into subgroups. Sort of looking at trees individually, and then looking at groups of trees, and then looking at the forest.
I also think that we may be on the right track with the wildcard hypothesis. I am not emotionally attached to it. I think that the high frequency symbols that do not have cyclical relationships could also be 1:1 substitution or filler. But the more I think about it, the more wildcards makes sense. Zodiac knew about diffusion. Why would he defeat the purpose of using multiple symbols to represent the letters with mid-range count, and then make frequency attack easy for the high count letters? Fillers is a possibility as well.
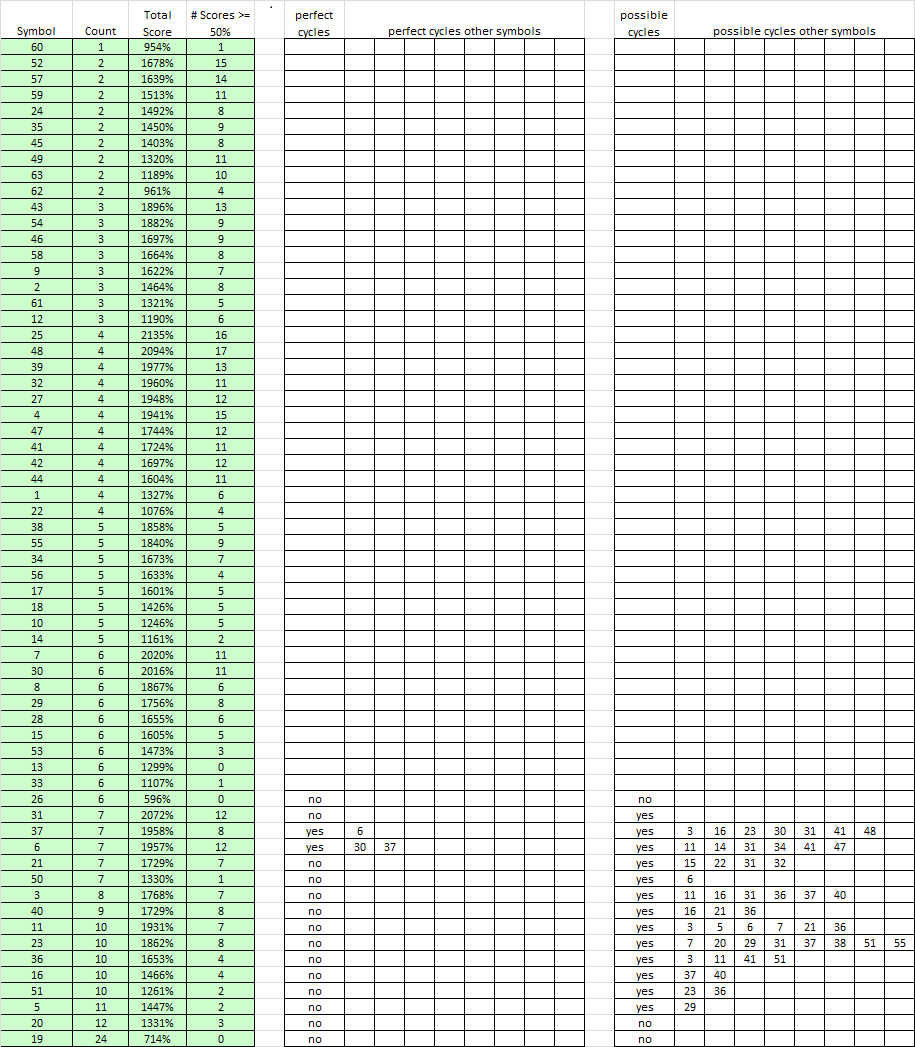
I have been analyzing the 340 a little bit this morning, here is the table of all higher frequency symbols:
Also, here is a simple scatter graph of the analysis, with count on the X axis and total score on the Y axis. Note that if a symbol is in a cycle with other symbols, then their count will be roughly the same. They would cluster together, at least vertically, on the graph. The upper left is a large clustering of mid-range count symbols that have a lot of cycle relationships with each other. On the lower left would be a few low-range count symbols that are probably 1:1 substitution for low frequency letters.
Some of the below is redundant, but I wanted to be more thorough today.
The proposed wildcards are in red. They are high in count and do not have strong cycle relationships with other symbols.
5 has some cycling with 29 (5 5 29 5 5 5 5 29 5 29 5 29 5 29 5 29 5). Score 59%.
51 has some cycling with 23 (23 23 51 51 23 51 23 51 23 51 23 51 51 51 23 51 23 51 23 23). Score 55%.
51 has some cycling with 36 (36 51 51 51 36 51 36 51 36 51 51 36 51 36 36 36 51 36 51 36). Score 50%.
Part of my analysis is a little bit subjective. You could flip a coin all day long and get patterns like these of which there are thousands. But see the Alternative Possibilities for 11, 23, 36, and 51 below.
Note 26 and 50 (purple) have counts of 6 and 7, but have little or no cycle relationships. all of the other symbols of that count are in cycles, but these are not.That’s what separates them out as a group. They are either 1:1, wildcards or filler. I am suggesting that they could represent low frequency letters. Zodiac didn’t feel the need to put them in cycles, but they appear in higher frequency than Zodiac anticipated because of his choice of words. Thus, they set apart from the other symbols.
Symbols 16 and 40 (blue) are in a strong cycle together (16 40 16 40 16 16 40 16 40 16 40 16 40 16 40 16 16 40 40), however I learned with Experiment 3 J-ST that this can happen quite by chance, and be a false cycle. Or they could simply represent a letter with a 19 count as a two symbol cycle. 16 and 40 do have some weak to medium cycling with other symbols, and I don’t know what to make of this. I am hoping that they are not cycled wildcards because of their count, but have considered that possibility.
Symbols 11 and 36 (black) cycle fairly strong together (11 36 11 36 11 36 11 36 11 11 36 36 11 36 36 11 36 11 36 11), and the analysis is the same as above. They both cycle weak to medium with several other symbols.
Symbol 23 (green) cycles with several other symbols, including:
with 31 (23 31 23 31 23 31 23 31 23 31 23 31 23 23 23 23 31). Score 65%, could be random.
and 37 (23 37 23 37 23 23 37 23 37 23 37 23 37 23 23 37 23). Score 65%, could be random.
and 51 ((23 23 51 51 23 51 23 51 23 51 23 51 51 51 23 51 23 51 23 23). Score 55%.
Symbols 3, 6, 7, 21, 30 and 31 (orange) mostly all have cycles with each other.
Alternative Possibilities for 11, 23, 36, and 51
11, 23, 36 and 51 all have the same count of 10, so theoretically there could be combinations of these symbols in cycles where Zodiac made symbol choices at random, which could exclude 51 from the group of proposed wildcards. Here are some possibilities:
Conclusion
Symbols 5, 19 and 20 are still the best candidates for wildcards, because they do not cycle with each other or any other symbol well. However, I now think Symbol 51 could possibly be in a cycle with Symbol 23 and represent the same letter. If that is the case, then Zodiac could have used only a few symbols to represent high frequency letters. I would have to put 51 in a borderline category.
S.T.
Something strange I noticed (as someone who is more English/thespian minded than Math minded):
Stage directions grid’s sort of look like the 9 sectioned grid people make to figure out ciphers. If Z was interested in plays and stage directions in theory, could he gave used it in some way for his cipher code? Again, this is probably a dumb crazy outlandish idea bc again I have no clue how this works. Just noticed similar structures. Thank you.
Btw thank goodness for you guys. I have NO clue what you are talking about – you all are way too intelligent for this ole gal. ![]()
I have an observation to make.
I have been scanning through the cycles that doranchak found:
https://docs.google.com/spreadsheets/d/ … sp=sharing
Starting with L=4, but increasingly with L=5 through L=7 as L becomes a higher number of symbols, I see a pattern. I am looking at bracketed cycles, which are perfect. And I am also looking at a lot of random ordering of symbols. The bracketed cycles are shifted to the left in many cases. We get two contiguous cycles, and then randomness.
So I am wondering what you guys think about that. Zodiac did the same thing on the 408 with high frequency letters such as E, I, O and T. See: viewtopic.php?f=81&t=267.
No doubt you guys are aware of that, but maybe that could help us narrow down the search for 20 or so needles in a haystack. Perhaps try and make a brute force search for cycles in the first, say, 170 symbols of the message (picked this number out of the air). See how may cycles we get as compared to a search in the entire 340. Do this for one L value first to see what happens. It seems to me that the probability of finding a highly improbable false cycle will be lower when working with a smaller number of symbols. Probably all of the cycles we are looking for are in the first half of the message. What I am wondering is, what if we made the haystack a lot smaller? Would that help?
On the other hand, we are looking for only 20 or so cycles. But there are way more than 20 cycles in the spreadsheet showing two contiguous perfect cycles and then randomness. What are we looking at here?
S.T.
Guys you have to excuse me for a while. Woke up dead tired and I feel the need to sit on the bench for a while.
@doranchak, I had not seen it. They are indeed exploring the same concept.
@smokie, I really like the ideas in your last post. I think we do need to take in account the positions on which the cycles are found and believe that a cycle with a more uniform spread over the cipher will be more likely to be actual.
@PinkPhantom and morf13, welcome to the thread. ![]()
No problem Jarlve. This stuff is very time consuming and hard work. I was taking a week off to paint my entire house… grew a short beard and got one wall painted.
Where messages are found
Yes, I agree that we should take into consideration where in the message cycles are found. On the one hand, examining only part of the message will eliminate a lot of false cycles. But on the other hand, examining the message as a whole will show us what cycles continue throughout and are more likely to be Z made.
Test cipher simulating wildcard, other team(?) and distribution of diffusion
If you want, you can delegate some tasks to me. I could make a cipher on my cipher key spreadsheet that simulates wildcard for you. If you feel more comfortable doing it yourself, that’s fine. I understand if you have something very specific in mind and feel more comfortable with that.
I found the Zodiac Killer Ciphers website this morning. I saw Jarlve’s reference in his last post about another team working on the same concept (?) and did a quick search but didn’t see anything. Can you point me in the right direction? ***
But on the website home page, doranchak was writing about making experimental ciphers to test any particular hypothesis. Now back to the discussion of Z340.
Regardless of who makes the test cipher, do you guys think that Z used higher L counts to diffuse higher frequency letters? What I mean is, in my analysis from yesterday, I found several symbols with count of 10 or 11. Some cycle with each other, and some do not, just looking at two symbols comparisons. Four of these symbols could be e, three t or a. Out of curiosity, how would any test cipher distribute the diffusion? We know that many of the symbols with count of 3, 4, 5 or 6 cycle with other symbols. But what to do with the high count symbols?
It sounds like reading Jarlve’s recent posts that if Zodiac used low L cycles for high frequency letters, then the message would have been solved by now.
Are the high count symbols in low L cycles that represent high frequency letters? Or what about in higher L cycles with randomized selection of intermediate symbols (ABCD ABCD ACBD ABCD ACBD)? Or could they be wildcards that are cycles with each other? If there are too many wildcards, doesn’t that minimize the confidence that we have in any solution? Probably depends on how many. You guys don’t have to answer that one in highly technical detail.
Another way to look at the symbols and cycles both separately and together?
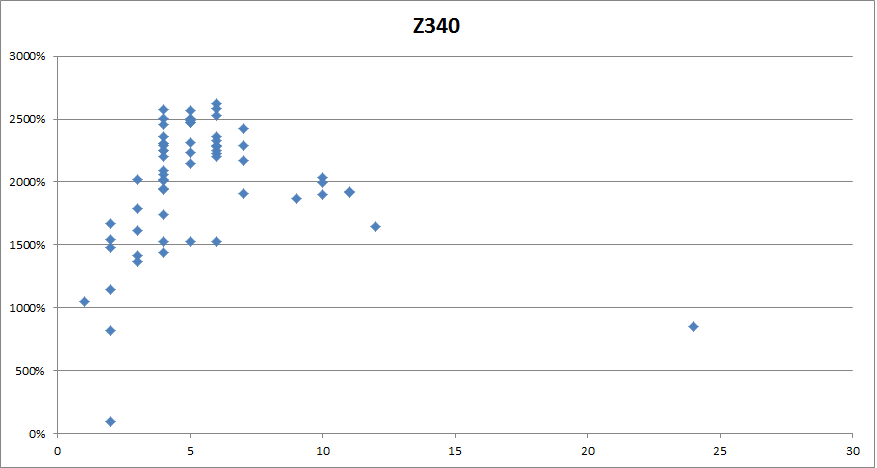
I was looking at the scatter graph and if you look at symbols with say, count of 2, 3, 4 and 5. If you look at the distribution of dots in each column, there is a pattern there as well. Do you see it? ** *** * * * (sideways).
The lower dots represent symbols that have low cycle scores, and the higher dots represent symbols that have high cycle scores. I am thinking that the higher dots may represent symbols that are in higher L cycles because they have higher total cycle scores. What do you guys think about that idea? Anyway, perhaps a different scoring formula would yield new information.
Or what about this idea. Use this or another method to score each individual symbol, and use that score to help score the cycles? Let’s say Symbol X scores higher in the scattergraph, and is found in cycles ABAB and ABCD. Does that affect whether ABAB or ABCD score higher? But then take into account scores for A, C and D in the formula as well. Could that help flush out the Z made cycles?
EDIT: Symbol B not Symbol X
Get some rest, Jarlve, and thanks very much for what you have done so far. I will consider shaving and painting another wall. Let me know about the test cipher. We could simulate the analysis two or three posts above, or something similar. Whatever you want to do.
S.T.
Here is my quick update – I’ve been playing around with my hillclimber that replaces the "+" symbols of the 340 to optimize the appearance of strong L=3 cycles.
This is the highest scoring modified Z340 at the moment:
HER>pl^VPk|1LTG2d NptB(#O%DWY.<*Kf) By:cM|UZGW()L#zHJ Spp7^l8*V3pO<VRK2 _9M1ztjd|5FPU&4k/ p8R^FlO-*dCkF>2D( #5<Kq%;2UcXGV.zL| (G2Jfj#Op_NYz^@L9 d<M*bSZR2FBcyA64K -zlUV|^J*Op7<FBy- U>R/5tE|DYBpbTMKO 2<clRJ|*5T4M.Z&BF z69Sy#7N|5FBc(;8R lGFN^f524b.cV4tdY yBX1*:49CE>VUZ5-D |c.3zBK(Op^.fMqG2 RcT*L16C<UFlWB|)L z^)WCzWcPOSHT/()p |FkdW<7tB_YOB*-Cc >MDHNpkSzZO8A|K;7
The best L=3 cycle in that cipher is:
[O<U] [O<U] [O<U] [O<U] [O<U] [O<U] [O<U] O<OO 7 1.1919525E-34 0.84 1.00124E-34
Here’s what it looked like in the original cipher:
OOU [O<U] [O<U] [O<U] O<O<OO
A before an after (original Z340 is on the left, modified version on the right):

Here are the other high-scoring cycles found in the modified cipher:
[O<K] [O<K] [O<K] [O<K] [O<K] [O<K] O<O<OOK 6 8.365804E-30 0.72 6.023379E-30
p [p<U] pp [p<U] [p<U] [p<U] [p<U] [p<U] [p<U] p<p 6 2.498017E-29 0.6666667 1.6653447E-29
[|O<] [|O<] [|O<] [|O<] [|O<] [|O<] || [|O<] |O|<OO| 6 2.12328E-28 0.6 1.273968E-28
[>D7] [>D7] [>D7] [>D7] [>D7] 5 3.2536162E-28 1.0 3.2536162E-28
[>S7] [>S7] [>S7] [>S7] [>S7] 5 3.2536162E-28 1.0 3.2536162E-28
[>Z7] [>Z7] [>Z7] [>Z7] [>Z7] 5 3.2536162E-28 1.0 3.2536162E-28
[DS7] [DS7] [DS7] [DS7] [DS7] 5 3.2536162E-28 1.0 3.2536162E-28
[tD7] [tD7] [tD7] [tD7] [tD7] 5 3.2536162E-28 1.0 3.2536162E-28
[YS7] [YS7] [YS7] [YS7] [YS7] 5 3.2536162E-28 1.0 3.2536162E-28
[tS7] [tS7] [tS7] [tS7] [tS7] 5 3.2536162E-28 1.0 3.2536162E-28
[YZ7] [YZ7] [YZ7] [YZ7] [YZ7] 5 3.2536162E-28 1.0 3.2536162E-28
[tY7] [tY7] [tY7] [tY7] [tY7] 5 3.2536162E-28 1.0 3.2536162E-28
[tZ7] [tZ7] [tZ7] [tZ7] [tZ7] 5 3.2536162E-28 1.0 3.2536162E-28
[>DS] [>DS] [>DS] [>DS] [>DS] 5 3.2536162E-28 1.0 3.2536162E-28
[tDS] [tDS] [tDS] [tDS] [tDS] 5 3.2536162E-28 1.0 3.2536162E-28
[tYS] [tYS] [tYS] [tYS] [tYS] 5 3.2536162E-28 1.0 3.2536162E-28
[tYZ] [tYZ] [tYZ] [tYZ] [tYZ] 5 3.2536162E-28 1.0 3.2536162E-28
[^<K] [^<K] [^<K] [^<K] [^<K] <^K^< [^<K] 5 1.9240067E-25 0.65217394 1.254787E-25
[^<U] [^<U] [^<U] [^<U] [^<U] <^U [^<U] ^< 5 1.9240067E-25 0.65217394 1.254787E-25
[^*K] [^*K] [^*K] [^*K] [^*K] * [^*K] ^* [^*K] 5 3.4671216E-25 0.625 2.166951E-25
[^*U] [^*U] [^*U] [^*U] [^*U] * [^*U] [^*U] ^* 5 3.4671216E-25 0.625 2.166951E-25
[VO<] [VO<] [VO<] [VO<] [VO<] O<V [VO<] O<OO 5 5.871599E-25 0.6 3.5229596E-25
^ [2z^] [2z^] 22z [2z^] [2z^] [2z^] [2z^] [2z^] zz 5 2.0629034E-24 0.5555556 1.1460575E-24
p| [p<|] pp [p<|] [p<|] [p<|] [p<|] [p<|] || [p<|] p|<p| 5 2.1631112E-23 0.46875 1.01395834E-23
Compare to the original cycles, https://docs.google.com/spreadsheets/d/ … sp=sharing (click the L=3 tab)
It’s not yet clear to me if this approach can distinguish between local and global optima (there may in fact be no global optimium). I think I will use one of Jarlve’s modified Z408 tests so I can see what kinds of cycles can be restored or discovered. Might also need to play around with the scoring.
No problem Jarlve. This stuff is very time consuming and hard work. I was taking a week off to paint my entire house… grew a short beard and got one wall painted.
That is funny. Working on the 340 can be a rush a times.
On the one hand, examining only part of the message will eliminate a lot of false cycles. But on the other hand, examining the message as a whole will show us what cycles continue throughout and are more likely to be Z made.
I like the idea of comparing halfs.
I found the Zodiac Killer Ciphers website this morning. I saw Jarlve’s reference in his last post about another team working on the same concept (?) and did a quick search but didn’t see anything. Can you point me in the right direction?
I was refering to the link doranchak put up: http://www.oranchak.com/king-homophonic-ciphers.pdf They describe a function REMOVE_HOMOPHONES which takes the most likely cycles of a cipher and replaces them with one symbol. For instance reducing a 63 symbol cipher to 50 symbols. I just glanced through it but I will read it when I’m better rested.
Regardless of who makes the test cipher, do you guys think that Z used higher L counts to diffuse higher frequency letters? What I mean is, in my analysis from yesterday, I found several symbols with count of 10 or 11. Some cycle with each other, and some do not, just looking at two symbols comparisons. Four of these symbols could be e, three t or a. Out of curiosity, how would any test cipher distribute the diffusion? We know that many of the symbols with count of 3, 4, 5 or 6 cycle with other symbols. But what to do with the high count symbols?
There should be cycles with a high L count (5-7). Such are also in the 408 and that is only a 53 cipher symbol. The whole idea behind the invention of homophonic substitution was to render frequency analysis useless. So the best thing you can do is make the symbol counts/frequencies as even/flat as possible.
Take for instance a 3 letter message with these frequencies.
e = 75
l = 23
z = 194
Let’s say we encode it to 10 symbols and the total number of characters here is 292. 292 over 10 is 29.2 characters per symbol perfectly even.
e = 75 / 3 = 25
l = 23 / 1 = 23
z = 194 / 6 = 32
Is decently flat. Maybe your asking if a letter could have an uneven cycle distribution such as "e=(24,4,4,4,4,4)". I have also wondered about that but don’t see any reason to do it that way. And the cipher would still solve in ZKDecrypto, it doesn’t matter much how you encode, perfectly cyclic or totally random, it will solve.
Get some rest, Jarlve, and thanks very much for what you have done so far. I will consider shaving and painting another wall. Let me know about the test cipher. We could simulate the analysis two or three posts above, or something similar. Whatever you want to do.
Thanks! You 2 btw.
It’s not yet clear to me if this approach can distinguish between local and global optima (there may in fact be no global optimium). I think I will use one of Jarlve’s modified Z408 tests so I can see what kinds of cycles can be restored or discovered. Might also need to play around with the scoring.
I follow your thinking.
I made a wildcard cipher (not by hand) with slight randomisation in the cycles (10%) adding wildcards after encoding where bigrams are found. I was a little bit too aggressive and there are now more bigrams in non-horizontal directions. One symbol is an obvious wildcard by frequency the others are not. In total there are fewer wildcard symbols than what we suspect in the 340 so it should be easier to solve. Have fun with it.
Symbolic and numeric version:
=`Y>[Ta1Tj3ZC@Ryk oqB7yRLu7-F?(ONo5 n:dx+VSK7%IgaU4PW 0tX!kFBApu;H3Ed(E :wuj=74+v7w#TSdC7 77?u7PV.z%qeUgSOb `RZSa7`A>dF7][73n LiwKyGvV#5HT=[pXe B%gUk(Hx?]7HFbBVg -ak7IO;d`1w%:AEj+ gqo.Su7PeCFVLVdi@ 0p3dUc+Kt50yN=7cb XKFv4:a]xTEkG>%NH z71`u51Bj(-d!TX77 `VRk?T5b7IcCOoAw7 7v%#:(XO+ZTFSEL0P @kP>g7BNi%WpHYun- .%kdjIbCzd:?7wgt; qdS#PO5GFLzceudPo Twik[ykUXn>VEp%Bv 1 2 3 4 5 6 7 8 6 9 10 11 12 13 14 15 16 17 18 19 20 15 14 21 22 20 23 24 25 26 27 28 17 29 30 31 32 33 34 35 36 37 20 38 39 40 7 41 42 43 44 45 46 47 48 16 24 19 49 50 22 51 52 10 53 32 26 53 31 54 22 9 1 20 42 34 55 20 54 56 6 36 32 12 20 20 20 25 22 20 43 35 57 58 38 18 59 41 40 36 27 60 2 14 11 36 7 20 2 49 4 32 24 20 61 5 20 10 30 21 62 54 37 15 63 55 35 56 29 52 6 1 5 50 47 59 19 38 40 41 16 26 52 33 25 61 20 52 24 60 19 35 40 23 7 16 20 39 27 51 32 2 8 54 38 31 49 53 9 34 40 18 17 57 36 22 20 43 59 12 24 35 21 35 32 62 13 45 50 10 32 41 64 34 37 46 29 45 15 28 1 20 64 60 47 37 24 55 42 31 7 61 33 6 53 16 63 4 38 28 52 58 20 8 2 22 29 8 19 9 26 23 32 48 6 47 20 20 2 35 14 16 25 6 29 60 20 39 64 12 27 17 49 54 20 20 55 38 56 31 26 47 27 34 11 6 24 36 53 21 45 43 13 16 43 4 40 20 19 28 62 38 44 50 52 3 22 30 23 57 38 16 32 9 39 60 12 58 32 31 25 20 54 40 46 51 18 32 36 56 43 27 29 63 24 21 58 64 59 22 32 43 17 6 54 62 16 5 15 16 41 47 30 4 35 53 50 38 19 55
Have a nice weekend smokie! ![]()
![]()
Mystery cipher:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 3 17 13 26 4 27 28 17 8 29 30 26 19 31 32 33 34 28 35 14 22 36 17 7 37 10 5 38 26 39 4 27 17 40 41 42 22 43 10 34 7 44 45 12 46 10 45 19 47 36 11 48 49 35 27 25 50 4 51 52 51 1 28 17 53 23 37 54 22 9 55 15 16 21 7 26 56 57 33 22 14 3 40 58 27 47 44 4 7 19 8 59 12 17 11 42 43 1 17 34 26 35 21 6 36 18 20 54 30 10 24 17 48 4 39 37 23 31 29 60 27 58 17 40 17 49 19 47 55 10 27 59 7 43 33 3 61 26 22 28 11 57 17 41 14 19 37 3 26 52 17 29 34 17 6 20 24 10 4 51 32 44 15 40 18 10 16 35 1 62 31 42 17 63 39 47 36 48 27 34 28 26 46 21 58 33 52 41 12 13 16 43 54 7 17 2 42 44 50 15 22 38 10 35 57 27 63 25 19 1 53 11 48 36 61 4 28 18 21 17 23 40 26 44 37 33 49 27 58 20 42 8 7 24 51 59 1 55 22 52 12 34 47 62 6 31 30 16 2 26 29 21 35 17 17 34 36 28 11 23 17 10 53 17 51 61 15 14 30 43 27 39 19 19 12 22 41 33 4 46 7 40 23 10 62 48 49 36 35 22 62 56 17 4 59 61 37 7 44 9 6 63 13 17 10 51 55 26 57 53 27 17 54 18 42
Jarlve, you want me to work on the mystery cipher, right?
Jarlve, you want me to work on the mystery cipher, right?
Yes. I also made a wildcard cipher one up. Feel free.
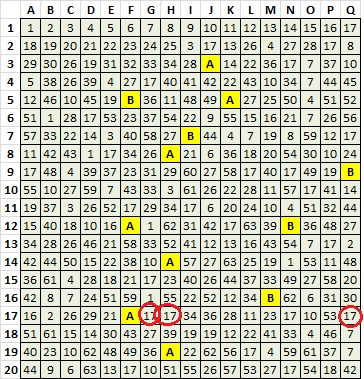
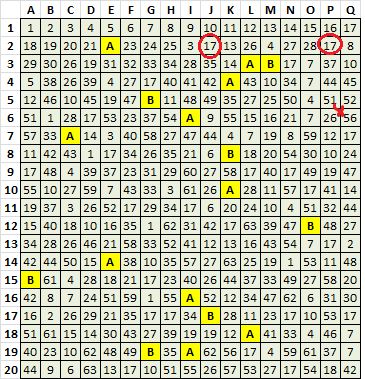
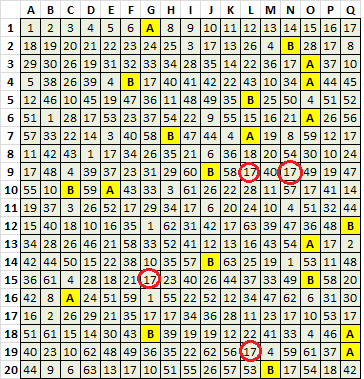
Mystery Cipher. Note that I always analyze in this order:
The Scatter Graph
Low count symbols with little or no cycle relationships lower left. Symbols with count of 4 to 7 in cycle relationships upper left. High count symbols with possible cycle relationships middle right. 17 far right. See High Count Symbols below.
High Count Symbols
17 is a 1:1 or wildcard. See Wildcards below.
10 is a 1:1 or cycles with 4 and 7 with random symbol selection.
27 is a 1:1, or cycles with 7 or 36 in a two symbol cycle with missing symbols.
26 is either a 1:1, or cycles with 27, 28 or 44 in a two symbol cycle with missing symbols.
22 is probably in a two symbol cycle with 36 with missing symbols, but also cycles with 4, 7 and 35 respectively with missing symbols.
4 cycles perfect with 7, and could be in a cycle 4 7 11 or 4 40 47 with missing symbols. Not sure if both is possible.
7 cycles perfect with 4, cycles with 22, 27 and 35 respectively with missing symbols in each, and could be in a three symbol cycle 7 35 36 with missing symbols.
Possible Wildcard Situations L=2 (could be part of L=3 or longer)
35 cycles with 47, and 17 shows up where a 47 is missing.
22 cycles with 36, and 17 shows up where one the first 36 is missing, but not where the second 36 is missing. 26 is there, but 26 cycles with other symbols. Not sure about this.
7 cycles with 27, and 17 shows up where three 7’s are missing.
Now to the second coat of paint on that wall…
S.T.
I’ve decided to return to working on my test cipher generator, since I need more controlled test ciphers to determine the actual effectiveness of the "wildcard explorer" hillclimber. I could make some test ciphers by hand but I think the automated approach I’m working on will be much more effective, especially since I will be able to generate ciphers that have Z340-like features but are constructed under varying hypotheses.