As already mentioned in the thread viewtopic.php?f=81&t=3196&start=1260#p70092, I am currently working on a new idea. It is based on the following assumption how Zodiac might have created z408 and possibly z340:
– Write down the plaintext on a normal sheet of paper. No matrix, just plaintext, as if you were writing a letter.
– The plaintext letters are substituted according to the order of the alphabet, not according to the order in the text (first all ‘A’, then all ‘B’ and so on). Overlooked letters are a possible explanation for the interrupted cycles in z408. I have described more details some time ago in the following thread:
viewtopic.php?f=81&t=3337
– Transfer the symbols one by one neatly into the final cipher. In this way, the supposedly skipped word "People" in z408 can be explained. See viewtopic.php?f=81&t=4281&p=69497#p69492
– Additional step for z340: The symbols are not transferred ltr ttb, but with a route or according to a pattern. As long as this route is not too complex, the final cipher remains cyclic with certain parts. Depending on the type of route or pattern, autosolvers would not find a solution.
– Suggestion of a route (which has already been invalidated by Jarlve): First fill n columns from top to bottom, then fill the rows. I call this procedure "Crossed Lines with n columns". This results in regular interruptions in the cipher. If trigrams "meet", pivots can occur. More about this later.
Even though crossed lines were obviously invalidated by Jarlves "Find sequential homophonic randomization" test, I would like to take a closer look at this procedure. It might serve as a template for further ideas.
Let’s start with something unspectacular. Small spoiler: At the end of the thread it gets a lot more exciting.
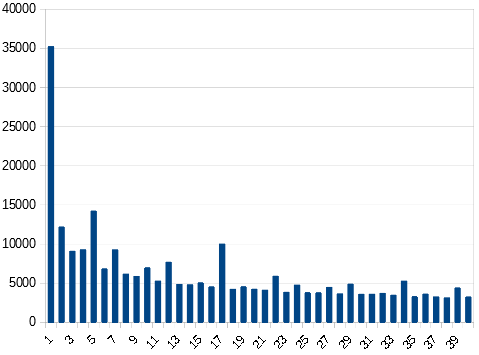
First, I determined whether a cipher generated in this way actually has a higher probability of pivots. I used a large text corpus and generated 250000 testciphers from it. I did the whole thing four times. Once without crossed lines, and once each with 2, 3 and 4 columns. Remember: First the columns are filled from top to bottom, then the rows. Here is the result:
No transposition, just substitution: 939 ciphers had 1 pivot 0 ciphers had 2 pivots Crossed Lines with 2 columns: 1697 ciphers had 1 pivot 2 ciphers had 2 pivots Crossed Lines with 3 columns: 2049 ciphers had 1 pivot 8 ciphers had 2 pivots Crossed Lines with 4 columns: 2030 ciphers had 1 pivot 14 ciphers had 2 pivots
Crossed lines actually lead to a higher pivot probability. However, I don’t think the very small increase is significant.
Here are the column indices I used:
2 Columns: 5, 13
3 Columns: 4, 9, 14
4 Columns: 2, 7, 12, 17
In the next test I determined for each of the 250000 test ciphers, on which period from 1 to 40 this has the largest number of bigrams. A list was created which periods were "most successful". Here is the result for ciphers without transposition:
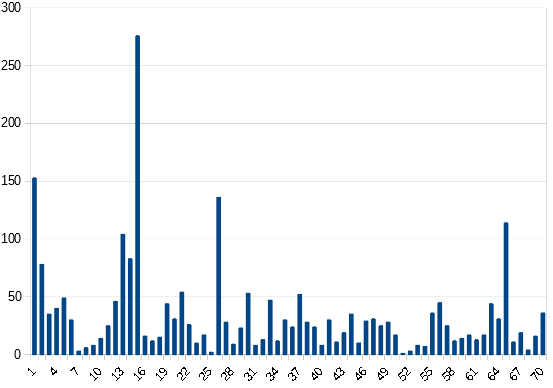
As expected, almost all ciphers (177335 of 250000) have a bigram peak on period 1. A few are in the range of period 2 to 7, but they are only outliers. For crossed lines with 4 columns (indices 2, 7, 12 and 17) the distribution is as follows:
This time P1 is still the most frequent, but not as dominant (60546 of 250000). Interesting are the mini peaks on P5 and P17. These are very small, but they appeared again and again in different tests with different column indices and reading directions. At this point I still have no idea where this comes from. If one can see the reason, one could possibly construct a P19.
Since you are limited to three pictures per thread, I will write the second part in a new post.
Translated with http://www.DeepL.com/Translator
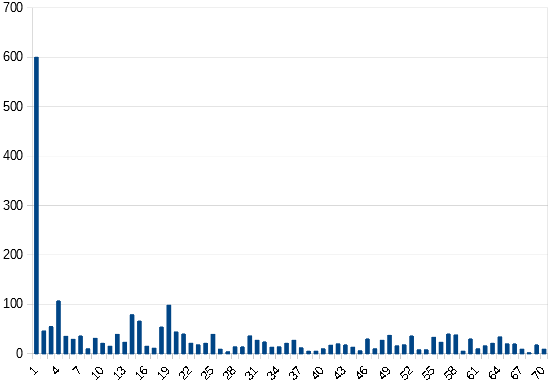
After the previous tests showed rather weak results, it now becomes a little more interesting. For the final test I didn’t create any new ciphers, but untransposed z340 with a four-column crossed lines matrix. If you take all possible combinations of four columns for a cipher with 17 columns, you get 2380 combinations. So I untransposed z340 with all 2380 possible four-column crossed linex matrices and just like in the last test I created a list with the most successful periods. Here is the result for bigrams:
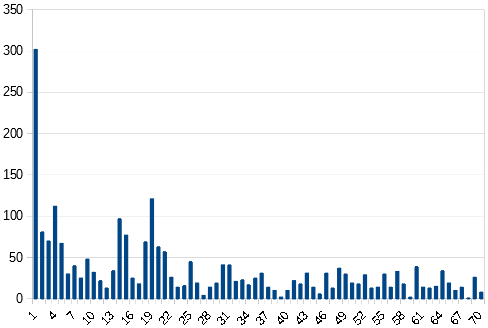
It is amazing that this type of untransposition causes z340 to have extreme peaks on P1, P15, P26 and P65. Also interesting is the exponential slope between Period 7 to Period 15 but it becomes even more amazing. Here is the distribution for trigrams:
600 of 2380 variations result in z340 having a trigram peak at period 1. I don’t know how this can happen. Maybe there is a very simple explanation. But for the moment I have absolutely no idea.
For quadgrams there is a very clear peak at period 52:
Does anyone have any idea what’s happening here? Am I missing something? If my confused description of "n columns crossed linex matrices" is too badly described, I’d be happy to make a video or a slide. It is difficult for me to describe this better, despite the translator.
Translated with http://www.DeepL.com/Translator
For crossed lines with 4 columns (indices 2, 7, 12 and 17) the distribution is as follows:
This time P1 is still the most frequent, but not as dominant (60546 of 250000). Interesting are the mini peaks on P5 and P17. These are very small, but they appeared again and again in different tests with different column indices and reading directions. At this point I still have no idea where this comes from.
I really like this work. We often think similar thoughts at the same time, and I am working on an idea that is very similar to this which I was going to discuss also this morning but will wait a while because of this.
Your idea is to try to find a simple way to make P19 and pivots at the same time, I think, but although it did not work well, some of the findings are very interesting. The P5 spike is intriguing. Your vertical inscriptions are 5 columns apart. so it appears that parallel inscriptions that are equally spaced can create this. If your inscriptions were 4 columns apart, then the spike would be at P4. Parallel bigrams at a particular spacing can show up as bigram repeats at that spacing. Or is it that the LRTB P1 to P4 bigrams are disrupted, and the LRTB P5 bigrams are the next most prominent spike in those messages? This could be useful information in the future. Thank you very much for doing this.
If you take all possible combinations of four columns for a cipher with 17 columns, you get 2380 combinations. So I untransposed z340 with all 2380 possible four-column crossed linex matrices and just like in the last test I created a list with the most successful periods. Here is the result for bigrams:
It is amazing that this type of untransposition causes z340 to have extreme peaks on P1, P15, P26 and P65. Also interesting is the exponential slope between Period 7 to Period 15 but it becomes even more amazing.[/attachment]
Help me understand how you came up with 2380 combinations. Are the columns evenly spaced, or just four columns anywhere? When you untransposed the 340, you chose four columns somehow, and then read them TB and transcribed them LRTB. Then after that, your read the remaining parts of the message by reading LRTB and transcribing LRTB. Correct?
19 – 4 = 15. That explains the spike at P15. P19 is dominant in the message. If you take out 4 columns, then the P19 repeats, the ones that are left, show up as P15.
We often think similar thoughts at the same time, and I am working on an idea that is very similar to this which I was going to discuss also this morning but will wait a while because of this.
Yeah, that’s actually happened a number of times. If we ever find a solution for z340, then probably on the same day too =)
I’m really looking forward to your idea.
Help me understand how you came up with 2380 combinations. Are the columns evenly spaced, or just four columns anywhere?
Just four columns anywhere. 2380 comes from "n over k (binomial coefficient)", in this case "17 over 4" So I test all possible combinations of four column indices.
When you untransposed the 340, you chose four columns somehow, and then read them TB and transcribed them LRTB. Then after that, your read the remaining parts of the message by reading LRTB and transcribing LRTB. Correct?
Yes, correct.
19 – 4 = 15. That explains the spike at P15. P19 is dominant in the message. If you take out 4 columns, then the P19 repeats, the ones that are left, show up as P15.
You’re right, that explains the P15 spike! Do you also have any idea for the P1 spike in the bigrams and the P1 spike in the trigrams?
Largo,
I like your hypothesis since it increases the likelihood of pivots. Also we can test it since the search space appears to be reasonable.
19 – 4 = 15. That explains the spike at P15. P19 is dominant in the message. If you take out 4 columns, then the P19 repeats, the ones that are left, show up as P15.
Clever!
Do you also have any idea for the P1 spike in the bigrams and the P1 spike in the trigrams?
The pivots are probably causing the p1 trigram peak since these are horizontal/vertical trigrams. Right?
This time P1 is still the most frequent, but not as dominant (60546 of 250000). Interesting are the mini peaks on P5 and P17. These are very small, but they appeared again and again in different tests with different column indices and reading directions. At this point I still have no idea where this comes from. If one can see the reason, one could possibly construct a P19.
Simple columnar transposition in a 17 by 20 grid creates a bigram peak at period 17 untransposed. The smaller period 17 peak is thus caused by the 4 columns in which the plain text direction is vertical (columnar).
The period 5 peak is probably caused by the skips of the vertical lines in some hard to understand way. For instance, a period 1 bigram can become a period 2 bigram if there is one vertical line in between. A period 1 bigram can become a period 5 bigram if there are four vertical lines in between. But a period 1 bigram can never become a period 6 bigram or higher because you never include more than 4 vertical lines so from there it will decline.
Example matrix of Largo’s idea:
81 82 83 84 1 85 86 87 21 88 89 90 41 91 61 92 93 94 95 96 97 2 98 99 100 22 101 102 103 42 104 62 105 106 107 108 109 110 3 111 112 113 23 114 115 116 43 117 63 118 119 120 121 122 123 4 124 125 126 24 127 128 129 44 130 64 131 132 133 134 135 136 5 137 138 139 25 140 141 142 45 143 65 144 145 146 147 148 149 6 150 151 152 26 153 154 155 46 156 66 157 158 159 160 161 162 7 163 164 165 27 166 167 168 47 169 67 170 171 172 173 174 175 8 176 177 178 28 179 180 181 48 182 68 183 184 185 186 187 188 9 189 190 191 29 192 193 194 49 195 69 196 197 198 199 200 201 10 202 203 204 30 205 206 207 50 208 70 209 210 211 212 213 214 11 215 216 217 31 218 219 220 51 221 71 222 223 224 225 226 227 12 228 229 230 32 231 232 233 52 234 72 235 236 237 238 239 240 13 241 242 243 33 244 245 246 53 247 73 248 249 250 251 252 253 14 254 255 256 34 257 258 259 54 260 74 261 262 263 264 265 266 15 267 268 269 35 270 271 272 55 273 75 274 275 276 277 278 279 16 280 281 282 36 283 284 285 56 286 76 287 288 289 290 291 292 17 293 294 295 37 296 297 298 57 299 77 300 301 302 303 304 305 18 306 307 308 38 309 310 311 58 312 78 313 314 315 316 317 318 19 319 320 321 39 322 323 324 59 325 79 326 327 328 329 330 331 20 332 333 334 40 335 336 337 60 338 80 339 340
The pivots are probably causing the p1 trigram peak since these are horizontal/vertical trigrams. Right?
I had that idea too, but I dropped it. The pivots do indeed generate repeated trigrams with my transposition idea. But only if the columns containing the pivots are hit when iterating the 2380 combinations. This is only the case in relatively few cases. If you destroy the pivots, the trigram count decreases like you said. But it is still siginificant at P1.
Cipher with destroyed pivots:
HERabcdVPeIfLTGgh Nb+BjkOlDWYmnoKpq BrstM+UZGWjqLkuHJ SbbvdcwoVxbO++RKg yzM+u12hI7FP+34e5 bwRdFcO-ohCeFagDj k7+KQl8gUtXGVmuLI jGgJp2kO+yNYu+9Lz hnM+0+ZagFBtrA#4K -ucUV+dB+ObvnFBr- U+R571E#DYBbXTMKO gntcRJIo7T4M2+3BF u#zSrk+NI7FBlj8wR cGFNdp7g40mtV41++ rBXfos4zCEaVUZ7-+ ItmxuBKjObdmpMQGg RtT+Lf#Cn+FcWBIqL ++qWCuWtPOSHT5jqb IFehWnv1ByYOBo-Ct aMDHNbeSuZOwAIK8+
Result:
Okay. Can you also remove these and test again? Thanks.
Input versus columnar 3: 3.23%
------------------------------
++R
+
+
t
R
t++
+
Sure. Do you mean to remove these symbols or to replace them with others?
I case of replacing those symbols:
HERabcdVPeIfLTGgh Nb+BjkOlDWYmnoKpq BrstM+UZGWjqLkuHJ SbbvdcwoVxbOjO4Kg yzM+u12hI7FP+34e5 bwRdFcO-ohCeFagDj k7+KQl8gUtXGVmuLI jGgJp2kO+yNYu+9Lz hnM+0sZagFBtrA#4K -ucUVDdB+ObvnFBr- U+R576E#DYBbXTMKO gntcRJIo7T4M2+3BF u#zSrk+NI7FBlj8wf cGFNdp7g40mtV41wQ rBXfos4zCEaVUZ7-H ItmxuBKjObdmpMQGg RtT+Lf#Cn+FcWBIqL ++qWCuWtPOSHT5jqb IFehWnv1ByYOBo-Ct aMDHNbeSuZOwAIK8+
However, ++R and ++t are in the opposite direction in the current case. The columns are read from TB and the rows from LR. The result is ++R / R++ and ++t / t++. These symbols do not generate trigrams. Nevertheless, the number of trigrams decreases significantly:
I am thinking that the trigram peak at period 1 is simply there because of the already existing trigrams in the 340. There are 2 horizontal trigrams plus the pivots. Seemingly the plus symbols are also involved. Because they appear grouped in so called box patterns and lead to easier creation of trigrams? Can you try it with destroying the pivots, the horizontally repeating trigrams and replacing every instance of the "+" symbol by a new unique symbol?
Edit: "the horizontally repeating trigrams" added.
P1 bigram repeats after removing all combinations of 4 columns in the 340, second highest spike… Perhaps all of the other bigram repeats at other periods are destroyed and P1 is what is left over.
P1 trigram repeats after removing all combinations of 4 columns in the 340, highest spike by far… I don’t know. Maybe you are detecting something.
The P52 quadram spike is interesting. You may be detecting something that we have detected before, but in a different way, or maybe this is something new.
Consider making a route transposition message with a distinctive spike at the height of the inscription rectangle, and performing the same test on that. See if you get similar or different results.
Maybe the P78 unigram repeats contribute to the P52 quadram repeat spike?
Can you try it with destroying the pivots, the horizontally repeating trigrams and replacing every instance of the "+" symbol by a new unique symbol?
What do you mean exactly? Should the 17 plus symbols that are not involved in the horizontal and vertical trigrams be replaced by a new symbol? So destroy the trigrams by replacing e.g. ++t / ++t with ++t / ++A and ++R / ++R and keep the 7 plus symbols? Then replace the remaining 17 plus symbols with e.g. ‘@’? Or replace ALL plus signs with new symbols? Then a total of 23 symbols would be added.
EDIT: Could you maybe post a cipher like this? Then I run the tests for 2, 3 and 4grams. This might be easier.
Consider making a route transposition message with a distinctive spike at the height of the inscription rectangle, and performing the same test on that. See if you get similar or different results.
Maybe the P78 unigram repeats contribute to the P52 quadram repeat spike?
Thanks for the idea smokie! I’ll put that on my todo list. At the moment I’m only working on z340 on weekends, so it might take a while.
Translated with http://www.DeepL.com/Translator
EDIT: Could you maybe post a cipher like this? Then I run the tests for 2, 3 and 4grams. This might be easier.
HER>pl^VPk|1LTG2d Np+B(#O%DWY.<*Kf) By:cM!UZGW()L#zHJ Spp7^l8*V3pO"$RK2 _9M'ztjd|5FP,&4k/ p8R^FlO-*dCkF>2D( #50Kq%;2UcXGV.zL| (G2Jfj#O=_NYz?@L9 d<MIbQZR2FBcyA64K -zlUV[^JOp7<FBy- U]R/5tE|DYBp.TMKO 2<clJR|*5T4Mb`&BF z69Sy#aN|F5Bc(;8R lGFN^f524b.cV4teg yBX1*:49CE>VUZ5-h |c.3zBK(Op^.fMqG2 RcTiL16C<mFlWB|)L no)WCzWcPOSHT/()p |FkdW<7tB_YOB*-Cc >MDHNpkSzZO8A|K;r