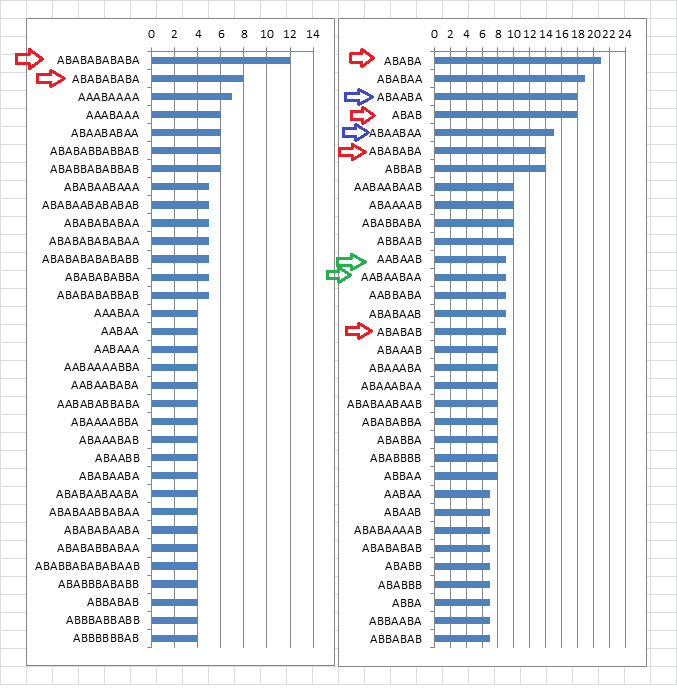
Here is my first observation. I reduced all L=2 cycles to AB and counted and sorted them by count for both the first three hundred and forty symbols of the 408 and the 340.

408. We know that he most perfectly cycled, and here are the top 20 by count and the consecutive alternations were detected against all other possible arrangements. Left column is by count, right column is the arrangement.

12 ABABABABABA
8 ABABABABA
7 AAABAAAA
6 AAABAAA
6 ABAABABAA
6 ABABABBABBAB
6 ABABBABABBAB
5 ABABAABAAA
5 ABABAABABABAB
5 ABABABABAA
5 ABABABABABAA
5 ABABABABABABB
5 ABABABABBA
5 ABABABABBAB
4 AAABAA
4 AABAA
4 AABAAA
4 AABAAAABBA
4 AABAABABA
4 AABABABBABA

340. There are a lot more arrangements with consecutive alternations, but the number of consecutive alternations is much lower ( see red ). Considering that detection worked well with the 408, I am wondering about ABAABA for starters ( see blue ). And then AABAAB ( see green ).

21 ABABA
19 ABABAA
18 ABAABA
18 ABAB
15 ABAABAA
14 ABABABA
14 ABBAB
10 AABAABAAB
10 ABAAAAB
10 ABABBABA
10 ABBAAB
9 AABAAB
9 AABAABAA
9 AABBABA
9 ABABAAB
9 ABABAB
8 ABAAAB
8 ABAAABA
8 ABAAABAA
8 ABABAABAAB

Maybe he just followed some different patterns besides just ABABAB. EDIT: Maybe he used different patterns for different letters.

Then there are "cycles" with odd numbers of symbols and even numbers of symbols. With odd numbers, there might have to be an option for removing the middle symbol. Like AAABABABABABABABAAA. Remove the middle B first, then make comparison AAABABABA ABABABAAA.

I am working on it to and hope to share observations in some time. It is funny that you mention cycles with odd and even number of symbols since that is also what I have been doing for palindromic cycles and I also let the middle symbol be ignored.

I don’t know (again) whether we’re talking about the same thing. Do you mean that the symbols of z340 should be sorted by even/odd and then examining the cycles? This improves the perfect 4- and 5 cycles found by azdecrypt.

Sort z340 even before odd positions:
Perfect 4-cycles:

5lX25lX25 (30)
5#8X5#8X5#8 (56)
5#825#825#8 (56)
5#X25#X25# (42)
58X258X258 (42)
5xX25xX25 (30)
PlX2PlX2P (30)
P3xXP3xXP (30)
P3x2P3x2P (30)
P3X2P3X2P (30)
P#8XP#8XP#8 (56)
P#82P#82P#8 (56)
P#X2P#X2P# (42)
P8X2P8X2P8 (42)
PxX2PxX2P (30)
3xX23xX2 (20)
#8X2#8X2#8 (42)

Perfect 5-cycles:

5#8X25#8X25#8 (72)
P3xX2P3xX2P (42)
P#8X2P#8X2P#8 (72)

Just to be on the safe side: Are you talking about the fact that Zodiac may have written the plaintext horizotally left to right, but encoded it in a different direction or something like that (odd before even or from top to bottom)? This would ensure that a plain text written in the usual direction does not contain any traitorous ngrams after substitution. At the same time, the result would look as if the encrypted text had been transposed instead of the plaintext. This technique would also be easy to realize with paper and pencil.
But that wouldn’t fit in with the fact that many of the lines don’t have any repetitions…… oh, never mind, I’m tired and should not post. I’m just trying to find ways to avoid ngrams and cycles without having to use complicated procedures.
Maybe I should deal with the topic a little longer before I post something again.

Largo:

Zodiac cycled his homophones when he encoded the 408, and there is evidence of some cycling in the 340 but not as much. I want to know why. I figure he may have used some other patterns besides perfect cycles, but still perfect. Or regional encoding, or perhaps some pattern that causes regional encoding. With 63 symbols I have 1,953 possible combinations of symbols. I use numbers for symbols because it is easier for me. For each of the 1,953 combinations, I delete all symbols in the array that are not the two symbols that I am looking at, and collapse the array. Then convert the symbols to either A’s or B’s.

The 408 is on the left, the 340 on the right. X axis is count of that pattern found out of all possible symbol combinations. For the 408 the top two were long sequences of consecutive alternations, or perfect cycles. The 408 has more of the longer pattern than any other pattern. The 340 has more combinations with ABABA than anything else, it is a shorter pattern but there a lot of them. Some are not true, some are false. I am wondering about ABAABA and ABAABAA. Since the method worked so well for the 408, I wonder if some of these are actually true patterns, actual letters.

To cause regional bias, or the symbols that appear exclusively in the top 6 and bottom 6 rows, I hypothesize that he did encode with regional or semi regional cycles. Moonrock’s idea. Something like this: AAABABABABABABABAAA. The A’s at the beginning and end would cause the regional bias. I can’t divide into equal chunks because there is an odd number of symbols, so I have to take out the middle symbol so I can compare. AAABABABA ABABABAAA. Except that this exact cycle wouldn’t cause the A to avoid the middle 8 rows.

Hypothesis

Maybe he did something like A B C A B C B C B C B C A B C A B C. That would cause the regional bias for A. If he did the exact same or very similar thing like this with more than one symbol, then maybe we can detect them and find out if they are statistically improbable or not. I am saying that maybe he did this to avoid the long perfect cycles, because with long perfect cycles a person could maybe identify them and use frequency attack. If you applied frequencies, then maybe you could see that the message was transposed. He could have hidden the homophone groups better by just randomly selecting homophones from their groups, but he liked to cycle and use patterns.

Wow, I’m really impressed how quickly you found out. However, I still wonder how to solve such an encryption completely. Have you succeeded in doing so? Do you have the plain text?

It is quite difficult.

A straightforward way is to go into AZdecrypt and go to Functions, Manipulation, select Raise periodic and enter From: 1, To: 340, Step: 2. This will create new symbols for every odd symbol that is not unique to the set of even symbols. In the case of your cipher it raises the amount of symbols to 127, a multiplicity of 0.373. That is certainly within the possibilities of AZdecrypt with 6-grams or higher but not a given. Though it is in fact much harder because 2 sets of unique symbols are interlaced with eachother. I have noted great difficulties in trying to solve such ciphers. Probably because of diminished internal structure and higher degree of freedom because of the interlacing.

I have not succeeded, but have the above running for half a day or so and may keep it running for a couple of days. If that fails I could still try some other ways. If this would be the 340 I feel we could solve it if we put our heads and efforts together.

Obviously, I underestimated that. If we once meet in Germany, I would be happy to donate as much Orangensaft as you like: D

Thank you for your hospitality!

Do you mean that the symbols of z340 should be sorted by even/odd and then examining the cycles? This improves the perfect 4- and 5 cycles found by azdecrypt.

This is not so unexpected. Because of the randomization in the 340, longer pieces of ciphertext decrease the odds of perfect cycles to appear.

Here are the periodic perfect 3-symbols cycles scores for the 340 by rows and columns. Period 2 by columns would mean odd/even, and by rows it means first half and second half of the ciphertext. These stats are not in the current AZdecrypt release but will be included for the next. Notice that the 340 through periods 2 to 5 scores much better by rows, this is also indicated by the positive percentage numbers (over 100%).

AZdecrypt periodic perfect 3-symbol cycles stats for: 340.txt
--------------------------------------------------------
Period 1:
- Row/column 1: 1060, 1060 (100%)
Period 2:
- Row/column 1: 3908, 3018
- Row/column 2: 2948, 1428 (154.20%)
Period 3:
- Row/column 1: 2516, 1306
- Row/column 2: 1908, 428
- Row/column 3: 1888, 1528 (193.50%)
Period 4:
- Row/column 1: 2232, 208
- Row/column 2: 2014, 176
- Row/column 3: 344, 204
- Row/column 4: 304, 276 (566.43%)
Period 5:
- Row/column 1: 804, 320
- Row/column 2: 328, 408
- Row/column 3: 2858, 436
- Row/column 4: 612, 96
- Row/column 5: 252, 284 (314.37%)

And now your latest cipher, which has individual sequential homophonic substitutions for odd and even positions. Notice the crazy numbers at period 2 by columns, a giveaway.

AZdecrypt periodic perfect 3-symbol cycles stats for: largo_oddeven.txt
--------------------------------------------------------
Period 1:
- Row/column 1: 1194, 1194 (100%)
Period 2:
- Row/column 1: 3856, 12686
- Row/column 2: 4806, 23112 (24.19%)
Period 3:
- Row/column 1: 1642, 2312
- Row/column 2: 1810, 392
- Row/column 3: 808, 2452 (82.62%)
Period 4:
- Row/column 1: 2276, 390
- Row/column 2: 1800, 554
- Row/column 3: 852, 1490
- Row/column 4: 44, 1766 (118.38%)
Period 5:
- Row/column 1: 984, 84
- Row/column 2: 736, 404
- Row/column 3: 96, 72
- Row/column 4: 180, 84
- Row/column 5: 32, 396 (195%)

340. There are a lot more arrangements with consecutive alternations, but the number of consecutive alternations is much lower ( see red ). Considering that detection worked well with the 408, I am wondering about ABAABA for starters ( see blue ). And then AABAAB ( see green ).

Many small cycles. I first noticed this when working on a hill climber that attempts to restore the cycles. With the 340 it was prone to create many perfect small cycles. From this I formed the hypothesis that the 340 may have more 1:1 substitutions than normal and that the key that remains outside of these 1:1 substitutions is generally quite efficient.

Zodiac cycled his homophones when he encoded the 408, and there is evidence of some cycling in the 340 but not as much. I want to know why. I figure he may have used some other patterns besides perfect cycles, but still perfect. Or regional encoding, or perhaps some pattern that causes regional encoding.

Yes, this is what we need to find out. It is worthwhile.

Hypothesis

Maybe he did something like A B C A B C B C B C B C A B C A B C. That would cause the regional bias for A. If he did the exact same or very similar thing like this with more than one symbol, then maybe we can detect them and find out if they are statistically improbable or not. I am saying that maybe he did this to avoid the long perfect cycles, because with long perfect cycles a person could maybe identify them and use frequency attack. If you applied frequencies, then maybe you could see that the message was transposed. He could have hidden the homophone groups better by just randomly selecting homophones from their groups, but he liked to cycle and use patterns.

We have not really defined regional cycles yet but common sense dictates it has to be something like that yes. More examples of regional cycles: 12121212 – 34343434 – 12121212 and 12121212 – 33333333 – 1212121212. That could indeed form some of the symbol imbalances we have observed (the 6-8-6 thing).

Jarlve:

The 340 is on the left and a shuffle is on the right. There are 18 of these for the 340 ABAABA and 15 of these for the 340 ABAABAA, which is just a one symbol extension of ABAABA.

The shuffles that I do so far might have a lot of one pattern, but the numbers here for the 340 are generally higher and I don’t get a pattern and an extension of a pattern.

The data suggests that one of his patterns was ABAABA ( L=2 only, because this may fit into a three or more symbol pattern ).

The data suggests that one of his patterns was ABAABA ( L=2 only, because this may fit into a three or more symbol pattern ).

Good idea to do coincidence counts of patterns in cycles and interesting results. Could you exclude the "+" symbol and do the same test?

Jarlve:

The 340 is on the left and a shuffle is on the right. There are 18 of these for the 340 ABAABA and 15 of these for the 340 ABAABAA, which is just a one symbol extension of ABAABA.

Cool test! I like this idea of counting sequences that are isomorphic to each other.

I noticed that there are only 18 cycles of the ABAABA type, but if you allow for matches where the sequence is imperfect (such as ABAABAB or AABAABA), then there are 196 sequences that have ABAABA in them (217 if you include ABAABAABA and ABAABAABAABA). Here are all the sequences:

http://zodiackillerciphers.com/combined … -z340.html

Is it even worthwhile to count the imperfect sequences? I kind of think it might be based on imperfect sequences in Z408. But I’m not sure how useful it is for the kind of analysis you are doing.

I don’t know where this is going but the test seemed to find a lot of perfect L=2 cycles for the 408. If Zodiac used a pattern, then maybe we could find the sequences. Some will be false, but it will boil things down a lot.

I just realized that I can copy and paste from this link into my spreadsheet and it will separate the data into columns. Thus eliminating the need for me to try to do all of this with a spreadsheet that finds the cycles.

http://zodiackillerciphers.com/longest- … ng-cycles/

So the work will be much easier.

As far as counting imperfect patterns, I am not sure. If he used a pattern different from perfect cycles for some of the letters, then there might be some with symbols left over at the end. If there are some very interesting patterns that we can find, and more than one of the same pattern making them highly improbable, then it would be interesting to see what happens if we rotate the message by 180 degrees.

The data above doesn’t show any patterns that include the + symbol because those would be from 25 to 36 long and there weren’t enough repeats to make the top twenty five list. There could be some repeats though.

Okay,

Here are the 2-symbol cycle ngram frequencies from 2 to 7 for the 340. I could have posted more but prefer to keep things manageable and investigate the ABAABA repeats. Will now work to get the sigma of each repeat versus randomizations.

AAAAAA: 398
ABAABA: 381
ABAAAA: 377
AABAAA: 374
AAABAA: 325
ABABAB: 316
ABABAA: 307
AAAABA: 292
ABAAAB: 279
AABAAB: 277

AZdecrypt cycle ngram stats for: 340.txt
--------------------------------------------------------

2-symbol cycles, 3-gram frequencies:
--------------------------------------------------------
ABA: 3173
AAA: 2255
AAB: 2209
BAB: 2117
BAA: 2106
ABB: 1860
BBA: 1594
BBB: 1583

2-symbol cycles, 4-gram frequencies:
--------------------------------------------------------
ABAA: 1481
ABAB: 1351
AABA: 1302
AAAA: 1207
BABA: 1037
ABBA: 938
BAAB: 937
BAAA: 907
AAAB: 859
BBBB: 794
ABBB: 789
BABB: 785
BBAB: 766
BBBA: 656
BBAA: 625
AABB: 572

2-symbol cycles, 5-gram frequencies:
--------------------------------------------------------
AABAA: 726
ABABA: 712
ABAAA: 701
AAAAA: 654
ABAAB: 642
AAABA: 557
BAAAA: 487
BAABA: 483
BABAB: 482
ABABB: 459
AAAAB: 442
BBBBB: 428
ABBAB: 425
AABAB: 413
ABBAA: 409
BABBB: 386
BABAA: 377
ABBBB: 366
ABBBA: 348
BAAAB: 342
BBBAB: 341
BABBA: 335
BBABB: 326
BBABA: 325
BBBBA: 308
BBAAB: 295
AABBA: 273
BAABB: 267
AABBB: 230
BBBAA: 216
BBAAA: 206
AAABB: 154

2-symbol cycles, 6-gram frequencies:
--------------------------------------------------------
AAAAAA: 398
ABAABA: 381
ABAAAA: 377
AABAAA: 374
AAABAA: 325
ABABAB: 316
ABABAA: 307
AAAABA: 292
ABAAAB: 279
AABAAB: 277
BBBBBB: 255
AABABA: 237
BABABA: 227
BAAAAA: 221
BAABAA: 217
ABABBB: 214
AAAAAB: 212
ABABBA: 210
ABBAAB: 207
BAAAAB: 199
BAAABA: 199
BAABAB: 197
ABBBAB: 186
ABBABA: 183
ABBABB: 181
BABBBB: 176
ABBBBB: 173
BBABBB: 172
BBABAB: 166
BABBAB: 165
BABAAB: 164
BABBBA: 157
BABABB: 157
BBBBAB: 155
BBBBBA: 154
ABBBBA: 154
ABBAAA: 151
BABAAA: 150
BBBABB: 145
BBBABA: 142
AAABAB: 138
ABAABB: 136
AABBAA: 135
BBAABB: 131
BBABBA: 125
BAABBA: 118
AABABB: 112
BBAAAA: 110
BBBBAA: 108
ABBBAA: 108
BABBAA: 106
AABBBA: 105
AABBAB: 105
BAABBB: 103
AABBBB: 103
BBAABA: 102
BBBAAB: 88
BAAABB: 75
AAABBA: 71
BBABAA: 70
AAAABB: 70
AAABBB: 63
BBAAAB: 63
BBBAAA: 55

2-symbol cycles, 7-gram frequencies:
--------------------------------------------------------
AAAAAAA: 252
AABAAAA: 216
AAABAAA: 192
ABAABAA: 186
ABAAAAA: 185
AAAABAA: 183
ABAAABA: 176
BBBBBBB: 162
ABABABA: 160
AAAAABA: 158
ABAAAAB: 156
ABAABAB: 149
AABAABA: 145
AABAAAB: 136
ABABAAA: 134
ABABAAB: 127
BAAAAAA: 125
AAAAAAB: 118
AABABAA: 114
BABABAB: 114
BAAAABA: 113
ABBABBB: 103
ABABABB: 100
AAABAAB: 98
AABABAB: 95
BAAABAA: 94
ABABBAB: 94
ABBBBBB: 93
BAABABA: 93
BABBBBB: 92
BAABAAB: 92
ABABBBA: 92
ABBABAB: 89
ABABBBB: 89
ABBAABB: 88
BBABBBB: 87
BBBBBBA: 86
BABBBAB: 86
BAABAAA: 85
ABABBAA: 85
BBBBBAB: 84
ABBAABA: 82
AAABABA: 82
BAAAAAB: 80
ABBAAAA: 79
ABBBABB: 79
BABAAAA: 78
BABAABA: 78
BBBABAB: 77
ABBBABA: 77
BABBABB: 75
BABABAA: 73
ABBBBAB: 71
BABABBB: 71
BBABBAB: 71
AABBABA: 69
BBBABBB: 69
ABBBBBA: 68
BBABABA: 67
BABABBA: 67
ABAABBA: 66
BBBBABB: 66
BBBBABA: 65
BBABBBA: 65
BAABABB: 64
BABBBBA: 63
ABBABBA: 63
BBBABBA: 62
BAAABAB: 61
BABBABA: 60
AAAABAB: 59
BABBAAB: 59
AABBAAA: 59
AABABBA: 59
AABAABB: 58
ABBBBAA: 57
BBABABB: 57
AABBAAB: 55
BAABBBB: 54
BBAABBB: 53
BAABBAB: 53
ABBAAAB: 53
BBAABBA: 52
AABBBBA: 51
BBBBBAA: 51
ABBABAA: 51
ABAABBB: 50
ABBBAAB: 50
BABAAAB: 49
BBAABAB: 48
BAABBAA: 47
AABBBAA: 47
ABAAABB: 47
AABABBB: 44
BBBAABB: 43
BBAAAAB: 43
BAABBBA: 42
BABBBAA: 42
BABAABB: 42
BBBBAAB: 38
AABBBAB: 38
BBABAAB: 37
BBAAAAA: 36
AAABABB: 34
BAAABBA: 34
AABBBBB: 34
AAAAABB: 32
AAAABBB: 31
AAABBAA: 31
BBAABAA: 31
BBBAAAA: 31
AAABBBA: 30
BAAABBB: 30
AAAABBA: 30
BAAAABB: 28
BBAAABB: 28
AAABBAB: 28
BBBBAAA: 28
ABBBAAA: 27
BABBAAA: 25
AAABBBB: 23
BBAAABA: 23
BBABBAA: 21
BBBAABA: 20
AABBABB: 19
BBBABAA: 19
BBABAAA: 16
BBBAAAB: 10

And here is the 408.

ABABAB: 777
BABABA: 643
ABAABA: 495
ABABBA: 491
AABABA: 461
ABABAA: 455
ABBABA: 415
BABBAB: 389
BABAAB: 374
BABABB: 352

AZdecrypt cycle ngram stats for: 408.txt
--------------------------------------------------------

2-symbol cycles, 3-gram frequencies:
--------------------------------------------------------
ABA: 3970
BAB: 3217
AAB: 2314
BAA: 2163
ABB: 2151
BBA: 1889
AAA: 1647
BBB: 1057

2-symbol cycles, 4-gram frequencies:
--------------------------------------------------------
ABAB: 2214
BABA: 1914
ABAA: 1502
AABA: 1398
ABBA: 1301
BABB: 1142
BAAB: 1115
BBAB: 1003
AAAB: 876
BAAA: 837
AABB: 781
ABBB: 673
BBAA: 661
AAAA: 641
BBBA: 588
BBBB: 384

2-symbol cycles, 5-gram frequencies:
--------------------------------------------------------
ABABA: 1351
BABAB: 1059
ABAAB: 804
ABABB: 751
AABAB: 749
BABBA: 714
ABBAB: 685
BABAA: 680
BAABA: 656
ABAAA: 594
AABAA: 570
BBABA: 563
AAABA: 500
ABBAA: 467
AABBA: 436
BAAAB: 432
ABBBA: 395
BBABB: 391
BAABB: 383
BABBB: 341
AAAAB: 329
BAAAA: 324
BBBAB: 318
AAABB: 317
BBAAB: 311
AAAAA: 263
AABBB: 255
BBAAA: 243
ABBBB: 224
BBBAA: 194
BBBBA: 193
BBBBB: 160

2-symbol cycles, 6-gram frequencies:
--------------------------------------------------------
ABABAB: 777
BABABA: 643
ABAABA: 495
ABABBA: 491
AABABA: 461
ABABAA: 455
ABBABA: 415
BABBAB: 389
BABAAB: 374
BABABB: 352
BAABAB: 334
ABAAAB: 311
BBABAB: 282
BAABAA: 277
ABAABB: 266
AABAAA: 265
AABAAB: 265
AAABAB: 252
BABBAA: 243
ABBABB: 242
BABAAA: 242
AABABB: 240
ABAAAA: 237
ABBAAB: 233
BAAABA: 230
BBABAA: 225
BBABBA: 223
BABBBA: 217
ABBBAB: 216
AAABAA: 214
BAABBA: 208
ABABBB: 203
AABBAB: 201
AAAABA: 194
AAABBA: 182
AABBAA: 168
ABBAAA: 166
BAAABB: 162
BBAABA: 161
BAAAAB: 155
BBBABB: 149
BBBABA: 148
BAAAAA: 146
AABBBA: 143
BBABBB: 138
AAAAAB: 136
ABBBAA: 130
BBAAAB: 121
BAABBB: 119
BBAABB: 117
AAAABB: 116
ABBBBA: 112
BBBBAB: 102
AAAAAA: 101
AAABBB: 101
BABBBB: 95
ABBBBB: 95
BBAAAA: 87
AABBBB: 87
BBBBBA: 81
BBBAAB: 78
BBBAAA: 77
BBBBBB: 65
BBBBAA: 64

2-symbol cycles, 7-gram frequencies:
--------------------------------------------------------
ABABABA: 511
BABABAB: 386
ABABAAB: 273
ABABBAB: 268
ABAABAB: 254
ABABABB: 240
BABAABA: 233
BABABBA: 228
BABBABA: 227
AABABAB: 211
ABBABAB: 210
BAABABA: 210
BABABAA: 208
ABAABAA: 204
AABABAA: 180
ABAAABA: 179
ABABBAA: 170
ABBABAA: 165
AABAABA: 154
ABAABBA: 153
AAABABA: 145
BABBABB: 145
AABABBA: 140
ABABAAA: 137
ABBABBA: 137
ABABBBA: 135
AABAAAB: 135
BAABAAA: 132
BBABABA: 132
ABBAABA: 129
BABAAAB: 127
BABBAAB: 126
AABBABA: 125
BAABAAB: 124
BBABBAB: 121
ABAAAAB: 119
BAAABAB: 119
BBABABB: 112
BABAABB: 111
AABAAAA: 110
BABBBAB: 108
ABAAABB: 108
BBABAAA: 105
BAABABB: 103
AAAABAB: 102
ABBBABA: 102
BBABAAB: 101
ABAAAAA: 101
BAABBAB: 100
ABBBABB: 99
AAABAAB: 99
AABAABB: 98
AAABAAA: 96
BABBAAA: 91
BAAABAA: 89
BABABBB: 89
BABAAAA: 89
ABBABBB: 88
BBBABBA: 86
ABBAAAB: 85
AAAAABA: 83
ABAABBB: 83
BBABBBA: 82
ABBAABB: 82
AABBBAB: 81
BBAABAB: 80
AAAABAA: 80
BABBBAA: 80
AAABABB: 80
BAAABBA: 79
BAABBAA: 78
AAAABBA: 78
AABABBB: 78
AAABBAA: 78
BAAAABA: 74
BBABBAA: 73
BBAABAA: 73
BBBABAB: 72
BAAAABB: 72
BAAAAAB: 72
AAABBAB: 67
AABBAAB: 67
BAABBBA: 67
AABBABB: 65
ABBBBAB: 61
BBBABAA: 60
ABBAAAA: 59
AABBAAA: 59
ABBBAAB: 58
AAAAAAB: 58
BAAAAAA: 58
BAAABBB: 57
BBAABBA: 55
BBAAABB: 54
AAABBBA: 53
BBAAABA: 51
BBBBABB: 50
ABBBAAA: 50
BBBABBB: 50
ABABBBB: 49
AABBBBA: 49
ABBBBBA: 49
BBBBABA: 46
BBABBBB: 46
BBAAAAA: 45
AAAAABB: 43
AABBBAA: 42
ABBBBBB: 41
BABBBBA: 41
BBBBBAB: 41
BABBBBB: 41
AAABBBB: 38
BAABBBB: 37
BBAABBB: 36
BBBAAAB: 36
ABBBBAA: 36
BBAAAAB: 36
BBBAABB: 35
AABBBBB: 34
AAAAAAA: 33
BBBBBBA: 32
BBBAABA: 32
AAAABBB: 30
BBBAAAA: 28
BBBBBAA: 28
BBBBAAA: 27
BBBBBBB: 24
BBBBAAB: 20

Jarlve, I ran a similar test but on long strings. This one happens twice for Z408:

ABABABABABABABABABAA

It has a sigma of 200 compared to 10,000 randomizations, the highest sigma encountered.

The corresponding sequences are:

9P9P9P9P9P9P9P9P9P99
PUPUPUPUPUPUPUPUPUPP

which are true cycles. So this test correctly identified some true cycles. But there are many false positives near the top as well such as:

ABBABBBBABBAAAABBBBBBB (also sigma 200)

MqqMqqqqMqqMMMMqqqqqqq
kqqkqqqqkqqkkkkqqqqqqq

ABAABAAAABAABBBBAAAAAAA (sigma 140)

qMqqMqqqqMqqMMMMqqqqqqq
qkqqkqqqqkqqkkkkqqqqqqq

The top sequence in Z340 was ABABAAAAAAAAAAAAAAAAAAABAABB (sigma 115):

+)+)+++++++++++++++++++)++))
+W+W+++++++++++++++++++W++WW

which I thought was interesting since "W" and ")" are some of the symbols exclusive to the first and last six lines.

I look forward to the results of your test of shorter strings. My test is prone to generate a large number of outliers.

One thing that I realized this morning. I assigned A or B depending on the symbol’s order of appearance. But ABAABA for 121121 is the same thing as BABBAB for 323323.

I have also considered other possibilities, such as trimming symbols off of the end of longer patterns so that all patterns in a group of patterns being compared have the same length.

EDIT: Oh, I see above that Jarlve already figured this out!

Thanks for the work, guys. It would be interesting to know if we can use this test, after developed, to identify patterns used in test messages. If the same patterns are used multiple times, then I think it could.