I got my L=2 cycle chunks spreadsheet done. I can compare all patterns regardless of length, or set an ngram length and the start position.

340

For ngram length of 6 and start position 1:

158 ABAABA
120 ABABAA
107 ABABAB
106 AABAAA
99 ABABBB
94 ABAAAB
93 ABBAAB
89 ABAAAA
87 ABBABB
87 AABAAB

If I try ngram length of 3 and start position 7:

214 ABA
183 AAB
181 BAB
161 BAA
157 AAA
144 BBB
141 BBA
100 ABB

EDIT: I did about 30 shuffles, and ABA was always somewhere on the list, but never on the top. AAA most often on the top.

This is still consistent with the ABAABA pattern, but if I go with length 9 start position 1, ABAABAABA is way down there:

25 AABAAAABA
24 ABAABABBA
22 ABABAAAAB
20 AABAABAAB
19 ABBABBBBB
19 AABAAABAA
17 ABAABAAAB
17 ABAABABAB
16 ABBABBBBA
16 ABBAABBBB
15 ABABBBBBA
15 ABAABAABA

If I go with length 4 and start position 7, it is still consistent with ABAABA:

89 ABAA
86 AABA
85 ABAB
84 BABA
80 AAAA
70 BBBB
69 BAAB
64 BBBA
64 BAAA
61 BABB

If I go with length 5 and start position 7, the pattern is down on the list:

49 AAAAA
43 ABAAA
42 ABABA
42 AABAA
38 ABAAB
37 BBBBB
32 BAAAA
32 BABBB
31 AAABA
31 BABAB

I fixed the bug with the missing ngrams, all results can be found here: https://drive.google.com/open?id=1mANVn … XAaqQb9nfS

Why are our counts so different smokie? I am excluding cycles with symbols that occur only once.

AAAAAA: 398
ABAABA: 381
ABAAAA: 377
AABAAA: 374
AAABAA: 325
ABABAB: 316
ABABAA: 307
AAAABA: 292
ABAAAB: 279
AABAAB: 277

Thanks Jarlve. So my modified 340 has slightly improved scores. Seems to be very easy to improve any kind of cycling score for Z340 with simple manipulations.

It must mainly depend on the initial randomness of the cycles in the cipher. It will be more easy to improve the state of the cipher by manipulations if its cycles are more random.

Could you test this cipher (randomized plaintext) versus your manipulations and how it performs versus the 340?

+E7'D*!$3*.)HSF1$
M&^*%Y6[ZU=($VQ,*
$R+>)*'/KG$(*8V$B
ITC#X3>E14#]+HLX
-3*=$)*@II^1HQ$[>
!YP^<RU:T,<?$IO;
#QK*5A"$9I0&CE*^.
+0D]M/JV$!K'*QR46
)-4Z"MI$8H1?9'?E&
7^A?(!-B)V?Z+55A
*Q_M9KX+G_/$2-4%E
]R!;SFL)_<*8"1I3&
#N=#HL';Y$O0Z*F@[
S!X.V"':$*-^V:DK
3UF,*E!8AB"TQ$7K>
[4=*["^H#$XME*T3
C49+[]PG>-;%5#X*
&N)T/RE1@?N3>2SI
Q#]P$P'[JU*;O*:1@
@K$*#$U:?RW2,Y*9E

I fixed the bug with the missing ngrams, all results can be found here: https://drive.google.com/open?id=1mANVn … XAaqQb9nfS

Why are our counts so different smokie? I am excluding cycles with symbols that occur only once.

AAAAAA: 398
ABAABA: 381
ABAAAA: 377
AABAAA: 374
AAABAA: 325
ABABAB: 316
ABABAA: 307
AAAABA: 292
ABAAAB: 279
AABAAB: 277

I don’t know. I am going like this for my symbols, with only 1,953 possible combinations ( I am using numbers for symbols ):

1 2
1 3
1 4
1 5
1 6
1 7
1 8
1 9
1 10
1 11
1 12
1 13
1 14
1 15
1 16
1 17
1 18
1 19
1 20
1 21
1 22
1 23
1 24
1 25
1 26
1 27
1 28
1 29
1 30
1 31
1 32
1 33
1 34
1 35
1 36
1 37
1 38
1 39
1 40
1 41
1 42
1 43
1 44
1 45
1 46
1 47
1 48
1 49
1 50
1 51
1 52
1 53
1 54
1 55
1 56
1 57
1 58
1 59
1 60
1 61
1 62
1 63
2 3
2 4
2 5
2 6
2 7

Etc. In other words, if I have two symbols, 1 and 2, I don’t repeat with 2 and 1. I just start with 2 and 3. I could have a problem, and will look at in the morning if you don’t know.

I fixed the bug with the missing ngrams, all results can be found here: https://drive.google.com/open?id=1mANVn … XAaqQb9nfS

Why are our counts so different smokie? I am excluding cycles with symbols that occur only once.

AAAAAA: 398
ABAABA: 381
ABAAAA: 377
AABAAA: 374
AAABAA: 325
ABABAB: 316
ABABAA: 307
AAAABA: 292
ABAAAB: 279
AABAAB: 277

I am not sliding through my patterns, only taking chunks like the first 6, etc. Maybe that is why.

I definitely have 158 of ABAABA. Out of 1,953 combinations, 1,825 have at least 6 symbols count, and out of those I have 158 ABAABA.

It looks like there could be some cycles that are regular, and some palindromic. At least when looking at shorter ngrams. Then when going to 6-grams and 7-grams, not as much. Maybe there is something else happening making it look like regular and palindromic.

None of the highest scoring patterns include P1 repeats.

Thanks a lot for doing this.

AZdecrypt cycle ngram stats for: 340.txt
——————————————————–

3-symbol cycles, 3-grams, sigma:
——————————————————–
ABC: 14.37 consistent with regular
BCB: 7.38
BCA: 6.55
BAA: -6.30
BBA: -5.72
ABA: 5.15
AAA: -5
BAC: 4.19
AAC: -3.84
ACC: -3.80

3-symbol cycles, 4-grams, sigma:
——————————————————–
ABCB: 12.77 consistent with palindromic
ABCA: 12.41 consistent with regular
ABAC: 9.64
BCBA: 6.57
BCAB: 6.54
BCBC: 5.62
BCAC: 5.31
BACA: 5.23
BAAA: -4.94
AAAB: -4.78

3-symbol cycles, 5-grams, sigma:
——————————————————–
ABCAB: 12.34 consistent with regular
ABCBA: 12.33 consistent with palindromic
ABCBC: 10.87
ABCAC: 10.45
ABACA: 10.32
ABACB: 8.30
ABCAA: 8.17
ABABC: 7.71
BCBAB: 6.41
BCABA: 6.31

3-symbol cycles, 6-grams, sigma:
——————————————————–
ABCABA: 12.14
ABCABC: 12.09 consistent with regular
ABCBAC: 11.14
ABCBAB: 11.01 consistent with palindromic
ABCAAC: 10.38
ABCBCB: 10.09
ABCACA: 9.71
ABCBCA: 9.48
ABACAB: 9.40
ABCACB: 9.25

3-symbol cycles, 7-grams, sigma:
——————————————————–
ABCABAB: 14.35
ABACABA: 12.64
ABCABCB: 12.53
ABCABAC: 12.17
ABCAABC: 11.79
ABCACAC: 11.46
BCABABC: 10.73
ABCACBC: 10.35
ABCBAAC: 10.34
ABCBAAB: 10.04

Here are the palindromic 3-symbol cycle sigmas:

340:
– Uneven palindromic cycles: 2.73 sigma
– Even palindromic cycles: -2.87 sigma
– Good example 1: OZO/OOZO/OZOO/OZO
– Good example 2: H>OHOO>OOO>OOHO>HO <— "H" is one of the symbols that only appears in the top and bottom 6 rows. Coincidence?

408:
– Uneven palindromic cycles: 3.44 sigma
– Even palindromic cycles: -1.33 sigma
– Good example: MD)MD)M)MD)DM)M)DM)DM)

smokie palindromic 1:
– Uneven palindromic cycles: 4.95 sigma
– Even palindromic cycles: -2.38 sigma
– Good example: 13 14 15 14 13 13 14 15 14 13 13 14 15 14 13 13 14 15 14 13 13 14 15 14 13

smokie palindromic 2:
– Uneven palindromic cycles: 8 sigma
– Even palindromic cycles: -2.10 sigma
– Good example: 22 23 24 24 23 22 23 24 24 23 22 23 24 24 23 22 23 24 24 23 22 23 24 24 23 22 23 24 24 23 22 23 24

At least it looks like the 340 is not using only palindromic cycles. The positive sigma’s that are noted both belong to some correlation between regular and palindromic cycles. I still find it striking that palindromic cycles are a good fit for some of our observations. It could explain the high unigram distance and the symbols that only appear in the top and bottom 6 rows. Throw in that both palindromic ciphers of smokie have a high count of ABAABA…

smokie palindromic 1:
ABAABA: 520
AABAAB: 425
BAABBA: 362
BAABAA: 356
ABABAB: 355
ABBAAB: 350
ABAAAA: 335
AAABAA: 318
AABBAA: 306
AABAAA: 303

smokie palindromic 2:
ABABAB: 484
ABAABA: 463
BABABA: 352
AABAAB: 322
BABBAB: 318
ABABAA: 317
ABBABB: 307
ABABBA: 306
AABAAA: 282
ABBABA: 279

Anyhow, both ABAABA and ABCABAB do meet the criterea for a new cycle type:

The alternating length cycle, alternates between shorter and longer substitution cycles: 12 – 1 – 12 – 1 – 12 – 1, 123 – 12 -123 – 12 – 123.

None of the highest scoring patterns have P1 repeats, so that could mean that if he used pattern(s) to encode, he was always shifting to the left or to the right in the homophone group.

Could you test this cipher (randomized plaintext) versus your manipulations and how it performs versus the 340?

z408:
jarlve nonrepeat 1: 5398
jarlve nonrepeat 2: 1148
pcs2: 884.93
pcs3: 418.90
jarlve m_2s_cycles: 2855.73
mean l2 sigma: 0.68

top 10 l2 isomorphic sequences (7grams) (10000 shuffles):
sequence count sigma
ABABABA 847.0 18.160410490244395
ABABBAB 480.0 11.674731469887355
ABAABAB 449.0 10.47899064531154
ABABAAB 456.0 10.436563335049671
ABABABB 402.0 8.693854286878198
ABBABAB 359.0 6.803592600362547
ABAABAA 319.0 5.941097321958316
AABABAB 318.0 5.360052729929763
ABAAABA 264.0 3.689005886061989
AABABAA 258.0 3.5331651626542886

top 10 l3 isomorphic sequences (7grams) (1000 shuffles):
sequence count sigma
ABCABCA 7869.0 24.999408939873156
ABCABCB 5103.0 18.31161522287286
ABCABAC 5105.0 17.423795588897878
ABCABAB 4287.0 16.934268075188402
ABCACBA 5012.0 16.924564555671292
ABCBACB 4667.0 15.704623454855238
ABCACAB 3822.0 14.330678138619596
ABACBAC 4312.0 14.288163211594838
ABABCAB 3691.0 13.841908057853795
ABACBAB 3701.0 12.904196365222267

z340:

jarlve nonrepeat 1: 4462
jarlve nonrepeat 2: 1599
pcs2: 247.85
pcs3: 62.36
jarlve m_2s_cycles: 2150.72
mean l2 sigma: 0.21

top 10 l2 isomorphic sequences (7grams) (10000 shuffles):
sequence count sigma
ABABABA 222.0 5.844441900977058
ABAABAA 220.0 5.242584748143618
ABAAABA 206.0 4.686882212721511
ABAABAB 162.0 4.272889915964004
ABABABB 150.0 3.519110242921718
AABAABA 187.0 3.4713584344638413
ABBABAB 147.0 3.2571199850212813
ABABAAB 145.0 3.126041816538682
ABABBAB 143.0 3.1028297955864357
ABABAAA 174.0 2.7589370221075473

top 10 l3 isomorphic sequences (7grams) (1000 shuffles):
sequence count sigma
ABCABAB 2461.0 8.926730621293041
ABACABA 2766.0 8.40224787183702
ABCBABA 2114.0 8.233752259265382
ABCACAC 2009.0 7.5333040117787755
ABACACA 2052.0 7.1840977681889875
ABCABCB 1945.0 6.2928693053865725
ABCBCAB 1788.0 6.246731527314625
ABACBAA 2016.0 6.139898905150641
ABCACAB 1780.0 6.108294272001644
ABCBCBA 1613.0 6.071643626247204

z340_best_l2 (row swaps):

jarlve nonrepeat 1: 4282
jarlve nonrepeat 2: 1600
pcs2: 271.57
pcs3: 100.25
jarlve m_2s_cycles: 2259.03
mean l2 sigma: 0.43

top 10 l2 isomorphic sequences (7grams) (10000 shuffles):
sequence count sigma
ABABABB 211.0 7.284436463918963
ABABABA 251.0 7.255567407863404
ABABAAB 205.0 6.853767465748607
ABABBAB 199.0 6.6383056463038415
ABAABAB 197.0 6.41323208669507
ABBABAB 196.0 6.354607427133724
ABAABAA 213.0 4.849364869570157
AABABAB 165.0 4.449153862529498
AABABAA 203.0 4.419034448049142
AABAABA 194.0 3.8002611171179503

top 10 l3 isomorphic sequences (7grams) (1000 shuffles):
sequence count sigma
ABACBAC 3168.0 12.417222932771136
ABACABC 2750.0 11.554946729038372
ABCABAC 3018.0 11.303875519396565
ABCABCB 2781.0 10.332438896245305
ABCABCA 3202.0 10.310879550150656
ABCBACB 2716.0 9.948564067712669
ABCACAB 2279.0 9.223538691010296
ABCBABC 2389.0 8.921247750208773
ABCACBA 2481.0 8.413720617150371
ABCABAB 2282.0 8.3308385320091

jarlve’s test cipher (randomized plaintext):

jarlve nonrepeat 1: 4093
jarlve nonrepeat 2: 2003
pcs2: 312.40
pcs3: 112.04
jarlve m_2s_cycles: 2202.52
mean l2 sigma: 0.26

top 10 l2 isomorphic sequences (7grams) (10000 shuffles):
sequence count sigma
ABABABA 288.0 8.524716890351055
ABABBAB 185.0 5.507408204578285
ABAABAB 173.0 4.771743952649954
ABAABAA 199.0 4.681375174729873
ABBABAB 170.0 4.421203972363935
ABAAABA 185.0 4.001828924979649
AABABAB 156.0 3.6420645472411346
AABAABA 167.0 2.910816918300106
ABABABB 143.0 2.761432443052834
ABABAAB 136.0 2.376032934176464

top 10 l3 isomorphic sequences (7grams) (1000 shuffles):
sequence count sigma
ABABCAB 2422.0 8.388144656829617
ABACBAB 2397.0 7.73510886675375
ABACABA 2440.0 7.660785792506601
ABCABAB 2291.0 7.574971844814827
ABCACAC 2076.0 7.456349879881403
ABABACB 2071.0 7.3535018703724555
ABABABC 1947.0 6.181813607710258
ABCBCBC 1794.0 5.59628400253989
ABABABA 2055.0 5.4425898366215115
ABCACAB 1859.0 5.341126391015531

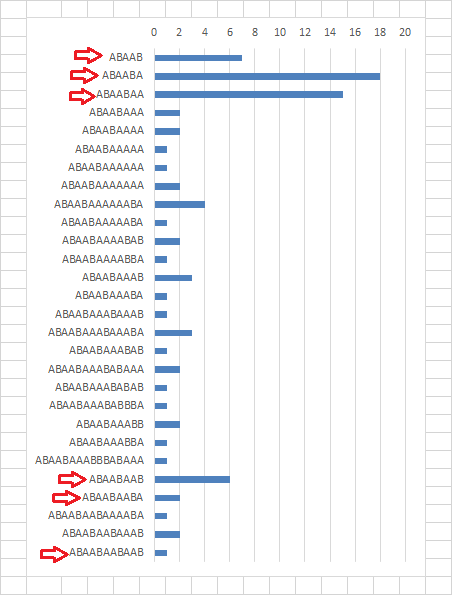
I sorted all of the L=2 patterns, regardless of length. Here is the section from ABAAB to ABAABAABAAB. There are normally a couple or a few in this range, but there are spikes with the ABAABA pattern. The ones on the bottom, the longer ones, If they were L = 2, then they would be good candidates for B, C, F, G, M, P, U, W, or Y.

If some of the ones on the top are parts of true cycles, then there may be several more symbols involved.

None of the highest scoring patterns have P1 repeats, so that could mean that if he used pattern(s) to encode, he was always shifting to the left or to the right in the homophone group.

What do you mean with P1 repeats? Please illustrate.

The ones on the bottom, the longer ones, If they were L = 2, then they would be good candidates for B, C, F, G, M, P, U, W, or Y.

If some of the ones on the top are parts of true cycles, then there may be several more symbols involved.

I do not understand at all smokie.

@doranchak, you said that the cycles in the 340 are easily improved by simple manipulations, I was wondering if my cipher would have the same result.

What do you mean by isomorphic sequences? Are these not just cycle ngrams?

For the 408, you list a 24.99 sigma for "ABCABCA 7869.0 24.999408939873156" while on my list it is "ABCABCA: 36.98". Where does this difference come from. Do you randomize the cipher or the cycles?

None of the highest scoring patterns have P1 repeats, so that could mean that if he used pattern(s) to encode, he was always shifting to the left or to the right in the homophone group.

What do you mean with P1 repeats? Please illustrate.

Looking at the 3 symbol cycles that scored highest, there are very few that have period 1 repeats. Example:

3-symbol cycles, 7-grams, sigma:
——————————————————–
ABCABAB: 14.35
ABACABA: 12.64
ABCABCB: 12.53
ABCABAC: 12.17
ABCAABC: 11.79
ABCACAC: 11.46
BCABABC: 10.73
ABCACBC: 10.35
ABCBAAC: 10.34
ABCBAAB: 10.04

The blue ones repeat A at period 1, but the highest scoring 7 grams do not have that. Each consecutive symbol is different. So, if he had a key that looked something like this:

E 1 2 3 4 5 6
T 7 8 9 10
O 11 12 13 14
A 15 16 17 18
I 19 20 21 22
N 23 24 25
H 26 27 28 29
S 30 31 32 33
R 34 35 36
D 37 38 39
L 40 41 42
U 43 44
C 45 46
W 47 48
M 49 50
G 51 52
Y 53 54
F 55 56
P 57 58
B 59 60
V 61 62
K
X
Z
Q 63
J

Each symbol selection he would move to the left or right, but not repeat a symbol. If he was encoding E, then he didn’t stay on one symbol and repeat. He would move to the left or right, but not stop, repeat, then change direction. That would be consistent with your idea that he was trying not to repeat symbols by row. Rather, instead of avoiding repeats by row, he kept shifting to the right or left, but didn’t stop and make a period 1 repeat. It’s just an idea, but could explain what you were talking about, not repeating symbols by row. Always shifting left or right would make it look like that. Just an idea, maybe too soon to say.

And by far the majority of 3 symbol cycles do not have any period 1 unigram repeats.

The ones on the bottom, the longer ones, If they were L = 2, then they would be good candidates for B, C, F, G, M, P, U, W, or Y.

If some of the ones on the top are parts of true cycles, then there may be several more symbols involved.

I do not understand at all smokie.

I counted the symbols, and used frequencies. The count of symbols makes these, if an ABAABA cycle, likely candidates for the above letters. Again, too soon to really say. But it is interesting to me that the patterns with the spikes are made up of the building block ABAABA.

@doranchak, you said that the cycles in the 340 are easily improved by simple manipulations, I was wondering if my cipher would have the same result.

Oh! OK. I should dust off my hillclimber and give it a try.

What do you mean by isomorphic sequences? Are these not just cycle ngrams?

To me an isomorphism is like an equivalence category.

Cycles DEFDEF and XYZXYZ are isomorphic because they can both be represented by the new sequence ABCABC.
So, multiple cycles can be included in this same "category" or isomorphism. It is a mathematic term that I’m probably not using correctly.

For the 408, you list a 24.99 sigma for "ABCABCA 7869.0 24.999408939873156" while on my list it is "ABCABCA: 36.98". Where does this difference come from. Do you randomize the cipher or the cycles?

I randomize the cipher. My methodology has these possible differences from yours which may account for the different results:

1) I count all substrings of length 7 in all the sequences. For example, ABCABCABC has substrings ABCABCA, BCABCAB, and CABCABC which are each counted.
2) Additionally, when considering substrings, I recompute the isomorphism. For example, "BCABCAB" is converted back to "ABCABCA".

I don’t yet know if my steps are necessarily beneficial or detrimental to this analysis. Perhaps I am over-counting certain kinds of sequences. But my intent was to catch patterns where the prefixes of the sequences tend to be random but the "real" patterns appear somewhere inside the sequences.

Odds to find all cycles for the ETAOIN homophones looks approximately like this (depending on the amount of homophones used for each letter):

For ETAOIN as

8 out of 63
7 out of 55
6 out of 48
5 out of 42
5 out of 37
4 out of 32

the odds are

1 : 3,872,894,697
1 : 202,927,725
1: 12,271,512
1 : 850,668
1 : 435,897
1 : 35,960

leading us to the previous being multiplicated

1.285 e+41

thus only a few hundred sextillion attempts to find the correct configuration..for the six most frequent letters only..

This is way worse than Powerball lottery..one might focus on letters with less homophones, however, which could still make sense (e.g. finding the homophones for the letters YOU), just wanted to comment on that before someone starts to crash his calculation with some memory error

QT