Hi,
this morning I had an idea for a new measurement method that could possibly determine whether a cipher was transposed or not. It is based on the discoveries that different column/row-offsets in z340 lead to significantly higher nGram numbers (viewtopic.php?p=56059).
My idea is to determine the period with the highest bigramm number for all possible offsets and to put the results into a list. Here’s the source code that illustrates this:
var map2Grams = new SortedDictionary<int, int>();
for (int y=0; y<cipherOriginal.Height; y++)
{
for (int x=0; x<cipherOriginal.Width; x++)
{
// Get a fresh copy of unmodified cipher
Snippet cipherShifted = new Snippet(cipherOriginal);
// Shift the cipher
if (x != 0)
cipherShifted.ShiftHorizontal(x);
if (y != 0)
cipherShifted.ShiftVertical(y);
// Track best periods
var best2GramPeriod = cipherShifted.GetBestPeriod(2, 170);
if (map2Grams.ContainsKey(best2GramPeriod.bestPeriod))
map2Grams[best2GramPeriod.bestPeriod]++;
else
map2Grams[best2GramPeriod.bestPeriod] = 1;
}
}
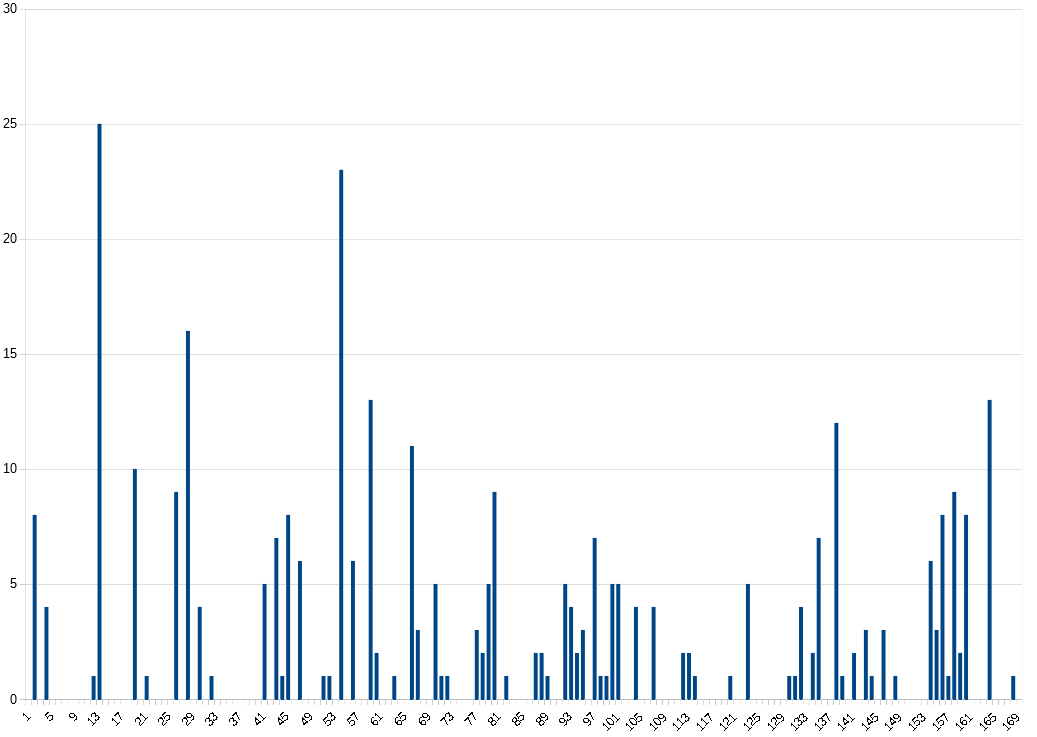
The z340 shows the following diagram:
The x-axis shows the periods 1-170, the y-axis shows how often which period was the "best" one. You can see very clearly that P19 is dominant, but there are also small disturbances. The periods 3, 4, 5, 16, 38 and 117 have the most irregularities. This is particularly interesting in that a 17×20 cipher also yields P16 in a diagonal transposition. Here again as a table:
3: 5 4: 8 5: 8 16: 38 19: 217 21: 2 38: 11 39: 1 54: 8 64: 1 76: 1 81: 1 84: 2 85: 3 86: 1 90: 1 91: 1 93: 1 97: 1 110: 1 115: 8 117: 10 123: 1 128: 1 129: 2 130: 1 138: 1 139: 1 142: 1 150: 1 157: 1
The third largest peak is on P38. This is not surprising as it is a factor of P19.
Let’s now take a cipher that we know to have a real P19 peak, but that doesn’t come from a straight P19 transposition. I used Jarvles cipher based on a Magic Square for testing (viewtopic.php?f=81&t=3591). Here is the result:
19: 326 32: 2 38: 6 41: 1 74: 1 97: 2 121: 1 131: 1
I have not used a diagram, because you can see very well that P19 stands out extremely. Again you can see that P38 has a small peak.
What happens if you have a cipher that has a bigram peak at P19, but that doesn’t result from a transposition? As we know, it happens occasionally that untransposed ciphers have significant peaks other than P1. Here is an example:
Plaintext (taken from the news archive at https://wortschatz.uni-leipzig.de/de ):
RNEDMAINLYWITHSTU DENTSWHOCONTINUET OGAMBLEBECAUSEITC ANBECOMEANADDICTI ONIDONTKNOWTHATIW OULDHAVEHADTHEDRI VETOSTARTMYOWNBUS INESSWITHOUTTHISP ROGRAMSAIDJAYSONE DWARDSFOUNDEROFTH EPOPULARPROVOHOTD OGSTANDJDAWGSANDS TUDENTOFTHEMARRIO TTSCHOOLBEIRUTLEB ANONMDASHTHEANTIS YRIANCOALITIONFRE SHOFFITSELECTIONV ICTORYBLAMEDLEBAN ONSPRESIDENTTHURS DAYFORTHEASSASSIN
Cipher (25% random cycles, raw IOC 2104)
SNmjJbCKI!8D0xW14 knL0X8yOiPM3DN6q3 OvcJfIrgshd4XtA0i eKfrhPJsbLcljBi1C OMCkPN3FKP80xd1D8 P5Glye7txbj2xmkTB 7n3PY0cU1J!O8Lg5Z CMoWW8D2yO633zAXQ TPwSdJYeAlEb!ZONp j8cTkWuP5KlqUOu0x rQPQ6GdVQSO7PxO0j PvX1eLkElb8wZbMjW 24ksN3Pu0ytJcTTBO 12ZhzPOHfmCU53Ing cKPLJleWx0yobM1DX !VCcNiOdGD1APKuSn XzOuuB3YrHni0CPL7 Ch1OT!gIeJojGpgbM PNZQVqWDkrK23z6SX lc!uOT0xmdYZcWXAL
If you let AZDecrypt analyze this cipher (Statistics -> Find plaintext direction), then everything points to P19. For the solver the cipher is no problem, it solves it as usual immediately. Let’s assume, however, that this is not the case. Then our assumption would be that a possible transposition is the reason and we would deal with P19. So what does the test described earlier show? This:
Apparently, this method is quite good for discovering "fake" periods. However, this test does not tell us what the "real" transposition is (in our case P1).
I wonder if more is possible with it. For example, the mini-peaks mentioned above could actually give hints on the structure of the cipher. How does the measurement behave if there are misalignments in a transposition? What is the effect of cycle randomization? What does it look like if the upper and lower half were transposed differently? What happens if about 90% of the cipher is transposed and the remaining 10% consists of a filler? What are the effects of frequent repetitions in plaintext?
I think there is still a lot to try out here. As always, the lack of spare time is the biggest opponent. I hope I can post something new soon, even if it is only the insight that the test is useless ![]()
Translated with http://www.DeepL.com/Translator
You might want to consider making plaintext transpositions, without substitution, with different sizes and shapes of inscription rectangles, to see if smaller versus larger, narrower versus wider, and shorter versus taller, have a tendency to create false spikes more than the other sizes. I made messages with multiple smaller inscription shapes quite a while ago, and was surprised to find false spikes more frequent if I recall correctly.
Looks cool Largo. Can you try it on a couple of ciphers that have 37 bigrams at p19?
Looks cool Largo. Can you try it on a couple of ciphers that have 37 bigrams at p19?
I ran some more tests. Among them was this one:
xmbGZO2Sb7nHoj3P2 ypQPS0OuJqkcKdzP4 TheUVAlrIOPFBLvuP SsVMC1bDNxOWQA0cG XdKjieJQY1ymSnBu! O4TokP8L2O8M!P5Jb !ZpqcuHOhFPuWrw8d !UClsVXvIDjAKwkO8 L3ztYBlo8eGFl8Sxb ZJcMCQ6Hd0pjJPPWq QOQ4He1DPMXf!AYZ5 ANvur8sTz6K2BKwQt UJC3WuOViP8YbLkJO SmuPTg4HIZc0GcW1h P5M3d0P1eHOuJDGA0 bU!QnVXPNKmH8pSqc YZBvLrl1O2xs8CGHP 8wTO7tMe7bIcBUZ1d 0CPNEOCN1TmWnU7of eXpbihPVkDMv3O0yq
Raw IOC: 2114
Unigrams: 60
Repeated Bigrams at P1: 25
Repeated Bigrams at P19: 37
Repeated Trigrams at P1: 1
It’s not that easy to find a cipher that has the most bigrams on P19 and that’s exactly 37. Maybe it would be better to use "(P19 – P1) > n" (in this case 37-25 = 12) as a criterion.
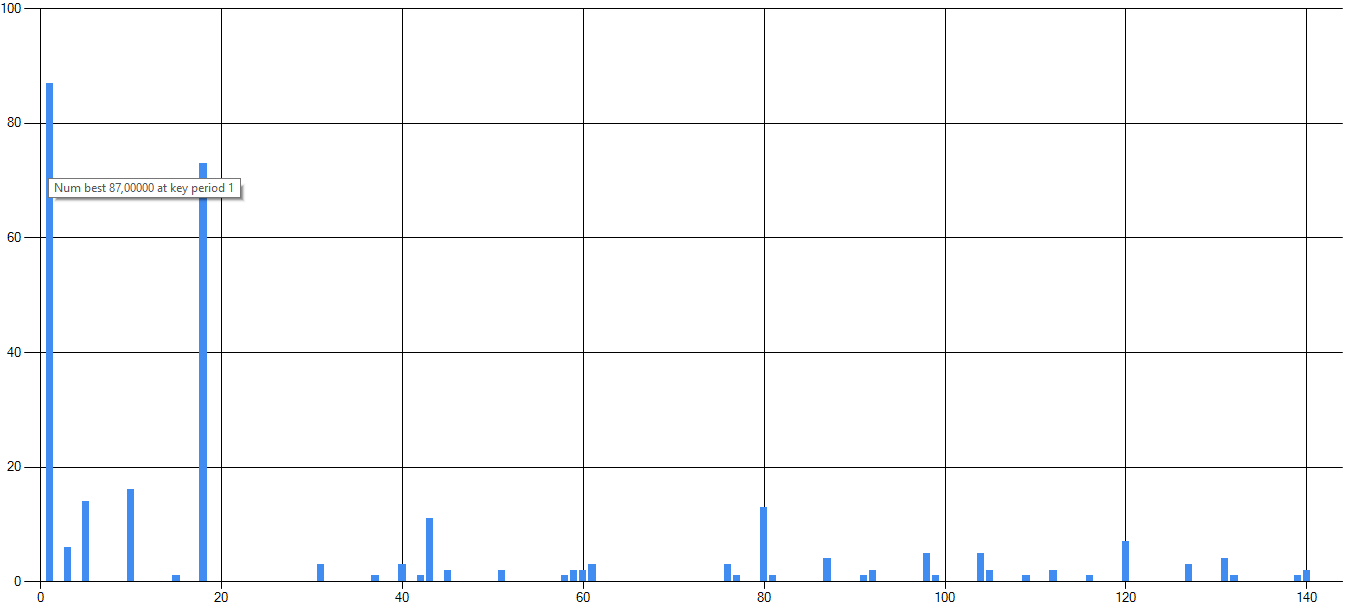
However, here again the test shows that the period is a false positive. Diagram:
You might want to consider making plaintext transpositions, without substitution, with different sizes and shapes of inscription rectangles, to see if smaller versus larger, narrower versus wider, and shorter versus taller, have a tendency to create false spikes more than the other sizes. I made messages with multiple smaller inscription shapes quite a while ago, and was surprised to find false spikes more frequent if I recall correctly.
That’s a good idea! I just added a chart dialog to Peek-a-boo, so that you don’t have to create a chart manually for all ciphers. So one can try it out very easy. Maybe I will be able to create a new version in the next days.
What would be great would be a scoring for the measurement. Simply only the number of spikes != best period is probably not enough. Does anyone have an idea?
Example:
The series of 11 inscription rectangles are 6 cells wide x 5 cells high, inscribe LRTB, read TBLR and transcribe LRTB into the 17 x 20 grid.
Since we are using inscription rectangles with 30 cells, there are 29 P1 bigrams in each inscription rectangle. There are 329 P1 bigrams in the intitial, untransposed message.
25 of the 29 P1 bigrams in each inscription rectangle will become P5, and 4 of the P1 bigrams in each inscription rectangle will become -P24.
Calculate how many P1 repeats there are, and the expected number of P5 repeats, approximately (25/29)*P1. If there is a spike at anything equal to or higher than this value, and not at P5, then have the computer remember the period ( "SP" ) and the number of repeats.
Is there any relationship between SP and its value and the width, height, or total number of cells in the inscription rectangle?
I said that I wanted to show the anatomy of a false spike once, and you liked the idea. It may have been a couple of years ago. I am sorry that I never did it, but it is still on my mind. I am still here and thinking about the 340 though.
If we know how false spikes are created, then perhaps we will know how to detect them. Perhaps make some variant of the idea above.
What would be great would be a scoring for the measurement. Simply only the number of spikes != best period is probably not enough. Does anyone have an idea?
I would keep it simple and just divide the amount of spikes by the maximum possible spikes such that your final number is between 0 and 1.
Hi,
If we know how false spikes are created, then perhaps we will know how to detect them. Perhaps make some variant of the idea above.
Many thanks for the idea! I don’t want to promise anything, because I don’t have much time. But I would like to test and implement it. Sounds promising.
I would keep it simple and just divide the amount of spikes by the maximum possible spikes such that your final number is between 0 and 1.
Thank you. With the next Peek-a-boo release I will include this. But I’m still looking for a way to evaluate results with two or more quite high spikes. In some tests I had e.g. a high peak at P1 and another peak at P18 (see below). I would also like to filter this somehow automatically. Maybe just count how many spikes are above average. I will give it a try.
Here are some more finds that might be interesting. However, I’m still not sure if my "Deceptive Periods" test is of any use at all.
If you only look at the lower half of z340, you will see an above-average peak at period 3 and NO hit for P19:
If you omit the upper and lower row and the first column, the following results:
Interesting that there are two distinct spikes at P1 and P18. Probably just an interesting coincidence, but let’s see where this leads…maybe I can discover regions that don’t belong to the cipher, but are responsible for P19.
Translated with http://www.DeepL.com/Translator
If you only look at the lower half of z340, you will see an above-average peak at period 3 and NO hit for P19
I find that interesting. If you read the message RLTB in groups of three symbols, ABC, then the P15 bigram symbols are both on either A, B or C. And the period 18, 36 and 54 unigram repeats, which make up the pivots, are also on either A, B or C. And the period 18 bigram symbols, reading the message LRBT, that have symbols that match P15 bigram symbols, are also either A, B or C.
Yesterday I checked again for a coincidence count spike at multiples of 3 reading RLTB, but there isn’t a pattern.
Here are some more finds that might be interesting. However, I’m still not sure if my "Deceptive Periods" test is of any use at all.
I would say that at least it may have specific use cases. Bigrams and alternatives may not always work for determining the plain text direction. But it is good to have them.
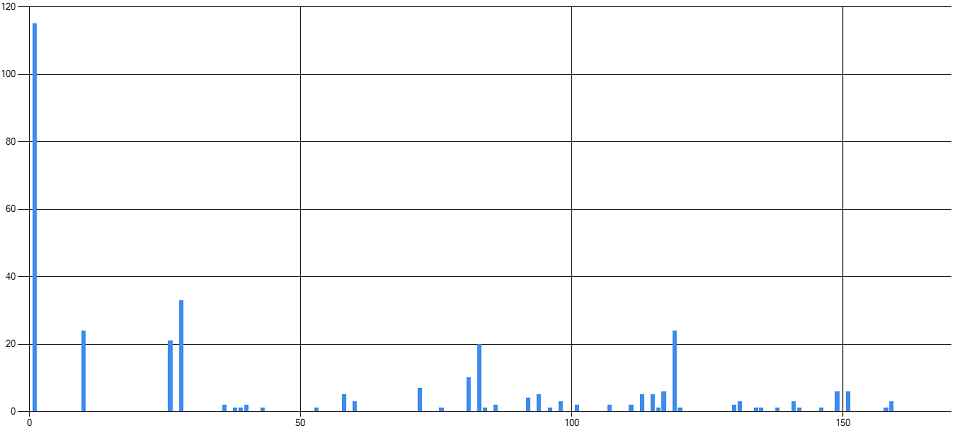
Here is smokie18e. It is a p1 cipher but smokie changed symbols or letters around to create a fake period at p19. Your test scores p19 at 158. What do you think?
>^DWZI:6>+[OgY`MM 4)Q<$GaW-12c9f80] ;NWF.O8gY,-ZeISUT <M:.B:G[+>)K4W+1b Z6`)KWRZ$BI_.A$5 .U>ZZO"0Z`8,9YBb; N.:.QW&`<IW.[gF/$ +SLV<.,ZV`<`^DID, 1<R[M`#^.aO59Nf*] )W-Z4cI<`F*Q08Bh> ;5h6[,:Q2GZ9]W`(4 fKSM)1J<..FRZA0N PIOW-]8Z[Z9V..5S. 7WL>f$C6Z>,M[`:Oe N<W.[2.BJZ,R6I[G- acZ#.Dg)%:g:-Z8TV IA)>W"<`P]fg)Z9M, R[WI-IG..O:/.WU4< ZBY4Z)*+><^I&hD`L B)K(aD/W.]7>)KWR;
Here is smokie18e. It is a p1 cipher but smokie changed symbols or letters around to create a fake period at p19. Your test scores p19 at 158. What do you think?
Indeed, smokie18e shows a very distinct peak at P19, but also some noise beyond P19. It becomes clearer if you perform untranspose P19 and then generate the chart again:
The noise may be an indication that it is a fake P19. Unfortunately, this behavior does not show up with all fake P19 ciphers. Here again the example I posted above:
xmbGZO2Sb7nHoj3P2 ypQPS0OuJqkcKdzP4 TheUVAlrIOPFBLvuP SsVMC1bDNxOWQA0cG XdKjieJQY1ymSnBu! O4TokP8L2O8M!P5Jb !ZpqcuHOhFPuWrw8d !UClsVXvIDjAKwkO8 L3ztYBlo8eGFl8Sxb ZJcMCQ6Hd0pjJPPWq QOQ4He1DPMXf!AYZ5 ANvur8sTz6K2BKwQt UJC3WuOViP8YbLkJO SmuPTg4HIZc0GcW1h P5M3d0P1eHOuJDGA0 bU!QnVXPNKmH8pSqc YZBvLrl1O2xs8CGHP 8wTO7tMe7bIcBUZ1d 0CPNEOCN1TmWnU7of eXpbihPVkDMv3O0yq
This cipher also shows a lot of noise apart from P19. But if you perform untranspose P19, the noise is gone and you only have the peak on P1:
xQVbY8WkbOuuHHHC1 emPAD1MrOZQrOIO8G dXbSlNy!w8J48VZup H0pG0rxmP8LcHsicJ SPCbZOIOS5d3MeTP0 Dq8PiOuOWnJ!zC1z8 GGcwNh2JPQBbUtQD6 YcAYTEPSqFAu!CY6P KbW0ZOOVbkB0!ZlBH M2L1bB7Ck7cLcOpsl dXBkhUvtNDnKvG4qV o0fKJP!LM1MHduXTc X8p!wO5QreTvozPdo uvejAQSMnl7m3jPSK kHIGJYtm3V1bWO34s jPODFPZUudXOIn0PT Vi8hjlP5JP0P2cUy2 hMeLFA8WACTPNxB7q yeCJ2PKSqN3g1KsUo pU1QOuwxQvW4em8Zf
Now it gets interesting: Take the cipher and copy it into AZDecrypt. The transposition solver takes a very long time to solve it, although it would only need a simple transpose P19. Could something similar have happened with z340? I don’t know exactly how to describe it, but does AZDecrypt perhaps "concentrate" too much on high nGramm numbers at certain periods? Probably there is an option in the settings that I don’t know yet ![]()
I have changed my measurement method for testing purposes. Instead of collecting the best periods in a list, I added the number of nGrams per best period.
Before:
// Track best periods var best2GramPeriod = cipherShifted.GetBestPeriod(2, 170); if (map2Grams.ContainsKey(best2GramPeriod.bestPeriod)) map2Grams[best2GramPeriod.bestPeriod]++; else map2Grams[best2GramPeriod.bestPeriod] = 1;
After:
// Track best periods var best2GramPeriod = cipherShifted.GetBestPeriod(2, 170); if (results.ContainsKey(best2GramPeriod.bestPeriod)) results[best2GramPeriod.bestPeriod] += best2GramPeriod.nGramCount; else results[best2GramPeriod.bestPeriod] = best2GramPeriod.nGramCount;
This helps to visualize the noise more clearly. However, this does not make the test significantly more meaningful.
Translated with http://www.DeepL.com/Translator
Try to solve it as a regular homophonic cipher, not a transposition. That might be the one where I manipulated the key until I got a false spike at P19.
Try to solve it as a regular homophonic cipher, not a transposition. That might be the one where I manipulated the key until I got a false spike at P19.
Sorry for the misunderstanding. The cipher that takes so long to solve is my example cipher from above. It got a fake P19 peak, but is P1. If you apply "Untranspose P19" to it, it has a peak at P1. This seems to challenge AZDecrypt.
The noise may be an indication that it is a fake P19. Unfortunately, this behavior does not show up with all fake P19 ciphers.
I have played around with your test in Peek-a-boo and I really like it.
I have changed my measurement method for testing purposes. Instead of collecting the best periods in a list, I added the number of nGrams per best period.
Do you have some graphs?
Now it gets interesting: Take the cipher and copy it into AZDecrypt. The transposition solver takes a very long time to solve it, although it would only need a simple transpose P19. Could something similar have happened with z340? I don’t know exactly how to describe it, but does AZDecrypt perhaps "concentrate" too much on high nGramm numbers at certain periods? Probably there is an option in the settings that I don’t know yet
The transposition solver uses bigrams to help its search, though it can be disabled by changing "(Substitution + transposition) Search states" to 1. Then AZdecrypt will only use its n-gram score. You can also reduce the search space by changing "(Substitution + transposition) Operation stack size" to 1. I tried with both and it quickly found a reasonable solution to your cipher. Look to the image to see what I’ve added for the next release. It will make things much easier and understandable. The idea is to add all transpositions that are "simple" to this list, in other words, the transpositions that have a reasonably small search space. And the transpositions that have a potentially large search space can be called "keyed" and these need a specialized individual solver.

I have changed my measurement method for testing purposes. Instead of collecting the best periods in a list, I added the number of nGrams per best period.
Do you have some graphs?
Sorry, but my changed measurement method had a bug that corrupted the result. After fixing the bug, the new test is almost 100% similar to the old one. The differences are too marginal to be representative.
The transposition solver uses bigrams to help its search, though it can be disabled by changing "(Substitution + transposition) Search states" to 1. Then AZdecrypt will only use its n-gram score. You can also reduce the search space by changing "(Substitution + transposition) Operation stack size" to 1. I tried with both and it quickly found a reasonable solution to your cipher.
Thanks, that worked!
Look to the image to see what I’ve added for the next release. It will make things much easier and understandable. The idea is to add all transpositions that are "simple" to this list, in other words, the transpositions that have a reasonably small search space. And the transpositions that have a potentially large search space can be called "keyed" and these need a specialized individual solver.
This idea is very good! So you can easily test specific transpositions, I’m already looking forward to the release! Thank you for continuously enhancing AZDecrypt!
Translated with http://www.DeepL.com/Translator