besides that, transposition would require alphabetical letters, however Z had used symbols.
Hm…why should a transposition should require alphabetical letters? Imagine the following text to be encrypted:
ILIKEGRILLINGINTHESUMMER
Now put that text into a grid:
ILIKE GRILL INGIN THESU MMER!
Now rearrange the columns:
KLIIE LRIGL INGIN SHETU RMEM!
Now apply a homophonic substitution and you get a transposed homophonic cipher. Another way to do this is to cut the grid which contains the plaintext and rearrange it in a different order before applying the homophonic substitution. There are many other ways to transpose the plaintext.
But I totally agree with you: It does not make things easier =)
EDIT:
I have updated the documentation a bit. Currently I am testing an idea with skipped symbols (assumed as filler). A total amount of 164220 permutations are currently fed into AZDecrypt. Refer "Skipping Letters" section for more details
Largo, I am really glad that you are interested in the subject of detecting transcription skips.
Here is an idea. Make a route transposition message, and skip a plaintext when transcribing the plaintext into the transcription rectangle. If you do that, and then untranspose the message into a 17×20 grid. There will be a vertical line somewhere between two columns where the plaintext are misaligned, basically cutting words in half and splicing them with other words cut in half. The same thing happens when you add a null when transcribing into the transcription rectangle.
I gather that you already understand the concept, so here is the idea.
To detect the possible location of a transcription skip, make 340 new messages, with nulls inserted at position 1, 2, 3, etc. Then count the number of period 19 bigram repeats for each message. The null positions showing the largest increase in period 19 repeats are more likely to be the actual location of the skip. You can detect a transcription null in the same way, by making 340 new messages, skip a symbol at each of the 340 positions, and shift the symbols after the skip one position.
Sometimes the method works extremely well, and can detect the skip or null position exactly. Sometimes the method detects the general area of the skip or null. And sometimes the method doesn’t work at all because of the homophonic encoding or other variables.
The first four or so rows of the 340 have a high concentration of period 18 bigrams that share the same symbols as period 19 bigrams elsewhere in the message. That could indicate an incomplete inscription rectangle, or a few transcription skips.
The pivots are offset by 39 positions, and could be repeated words in an area where there are a couple of transcription nulls. If you delete the symbol at either position 165 or 166, and delete a symbol at either position 210 or 211, you can create a huge spike in the count of period 38 bigram repeats, which for a period 19 transposition scheme would be period 2 bigram repeats before transposition. You will get values at about where they should be.
So perhaps instead of trying to detect possible permutations of skip or null locations with the solver, try to detect them with increases in the period 19, 38 etc. bigram repeat counts. Then, take the permutations that cause the biggest increase in repeat counts, untranspose, and feed those to the solver. This may be more efficient.
A handful of transcription errors could cause a transposition message to be very difficult to solve, and is a very plausible explanation for our problems.
Thanks again for your interest in the subject.
So perhaps instead of trying to detect possible permutations of skip or null locations with the solver, try to detect them with increases in the period 19, 38 etc. bigram repeat counts. Then, take the permutations that cause the biggest increase in repeat counts, untranspose, and feed those to the solver. This may be more efficient.
Thank you for this great explanation. I will implement this into my python library! But I also think that there are some ways to create letter skips which can not be detected by an analysis like that (and assuming that the period 19 bigram repeats and the pivots are coincidences). Maybe you want to analyze the following cipher with your tools? I have put in a couple of random letters but the positions of those fillers are not random. They have a specific order.
ND1IlDo8JXc7XQ0nw F2+bXnjdlABjantTU XrIALi5AK5CMDlbdY sdIzqhiRnxwuuD7kF 5oUXCG0T2xlFdMbXS GL5q5ohInzNYMtXkS bfkUTYicKsXuDjqkL pgGYnXBwSexkUT5ti YI0RI1i5PkzLi7HYZ 7BH0uIQ0nzXpXnsFY #3kxQIu4paUiTLDjx TkdCsXXjeZuuXhp51 UXuG3TDqHHILldoiY V+s+wTYPA73Tc8XXj duuXsh2czUXhq0TTx DFdGkNc9tXrEJpwCw 2XUfNXxUXuuTzFF+z lXnxs2ZnsM2#ku5XQ 0UxqXGyQK0VlXvumk Mpxu+dQyUD+9vw8pj
Largo
-> If my english sounds harsh or impolite, please forgive me. My native languages are German, C++ and Python.
Largo,
I checked your message to find out if it is a route transposition, and am not sure that it is. There are more period 1 bigram repeats than any other period, but I tried to solve it with the solver programs and it doesn’t solve. Is it a route transposition?
Your English is fine. My language is English, and I am pretty good with Excel. I have not written a computer program in 30 years until this week, and am starting to learn JS.
I have not written a computer program in 30 years until this week, and am starting to learn JS.
This is a good idea. It is always useful and fun to learn a programming language. There is so much which can be done e.g. writing tools to make things easier. I hope you will enjoy learning js!
The cipher is not a route transposition. It is an english text written from left to right, top to bottom. The only thing I’ve done is putting some useless letters at specific positions. This prevents AZDecrypt from solving the cipher. Unfortunately I made a mistake in the previously posted cipher. The substitution was not cyclic, instead is was random (which is not a problem as long as the "nulls" are removed. AZDecrypt will solve it then).
Here is the cipher text with cyclic homophonic substition:
Cipher "Largo_1"
sdoclizwEXCqXQanL pFfbXtjDlAkjgRVTU XrIGNZ57KcCMdleiY 8DI1qhZntxsuudAB2 5oUXcGyTpPlFizbXv 7wCqIKh5RMLY1VXHS e+kUTYDcoNXuZjAB8 20GYnXHsrb3kUTCtd YI#R5zicaBKwD7HYZ qkBfuCQgVMXpXnLFY xyHPQIu42+UdTNij0 TkD58XXjeZuuXhpc1 UXuA3TdGBHCslioDY t#waLTYf7qgTINXXj ZuuX8hF5zUXhAxTTy d2iGksc9RXvJEpwCL FXUPNX+UXuuTK2p0M lXV38FDns12#BuIXQ aUf7XqgQoxtlXSumH zpyuPZQ+Ud04rwLFj
Now it may be a bit easier to analyze it. I have no idea how to find the positions of the "nulls" without knowing the pattern. I am curious if anyone can show me how to isolate them.
If you are interested in the solution please follow this link:
https://www.dropbox.com/sh/w0qrhsv9sx0a … FSKga?dl=0
Largo,
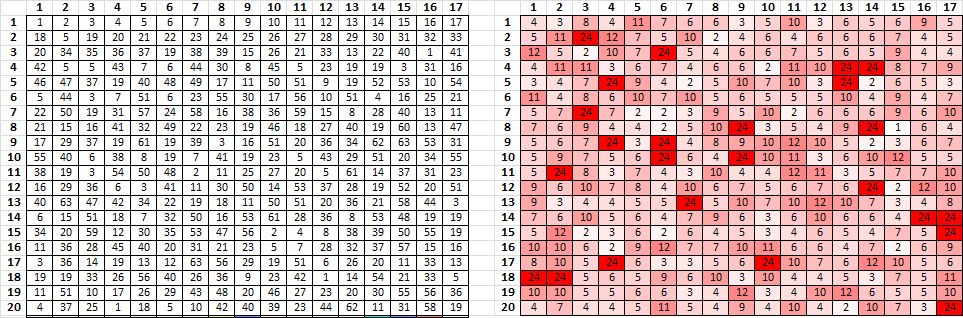
Here is your message converted to numbers for my spreadsheets. It is much more cyclic than the Z340.
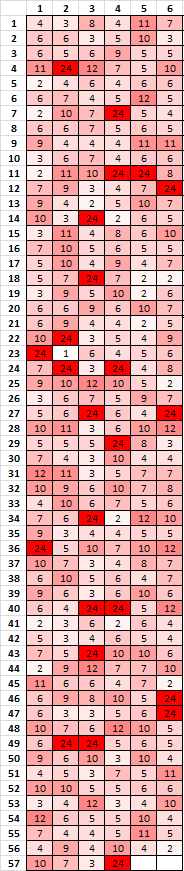
1 2 3 4 5 6 7 8 9 10 11 12 10 13 14 15 16
17 18 19 20 10 21 22 23 5 24 25 22 26 27 28 29 30
10 31 32 33 34 35 36 37 38 4 11 39 2 5 40 6 41
42 23 32 43 12 44 35 15 21 45 1 46 46 2 24 47 48
36 3 30 10 4 33 49 29 17 50 5 18 6 7 20 10 51
37 8 11 12 32 38 44 36 27 39 16 41 43 28 10 52 53
40 54 25 30 29 41 23 4 3 34 10 46 35 22 24 47 42
48 55 33 41 15 10 52 1 31 20 56 25 30 29 11 21 2
41 32 57 27 36 7 6 4 14 47 38 8 23 37 52 41 35
12 25 47 19 46 11 13 26 28 39 10 17 10 15 16 18 41
45 49 52 50 13 32 46 58 48 54 30 2 29 34 6 22 55
29 25 23 36 42 10 10 22 40 35 46 46 10 44 17 4 43
30 10 46 24 56 29 2 33 47 52 11 1 5 6 3 23 41
21 57 8 14 16 29 41 19 37 12 26 29 32 34 10 10 22
35 46 46 10 42 44 18 36 7 30 10 44 24 45 29 29 49
2 48 6 33 25 1 4 59 27 10 51 60 9 17 8 11 16
18 10 30 50 34 10 54 30 10 46 46 29 38 48 17 55 39
5 10 28 56 42 18 23 15 1 43 48 57 47 46 32 10 13
14 30 19 37 10 12 26 13 3 45 21 5 10 53 46 61 52
7 17 49 46 50 35 13 54 30 2 55 58 31 8 16 18 22
EDIT: O.K., I think that I understand what you are thinking. It is more than just two nulls, right? There is a pattern of nulls, similar to a message untransposed, correct?
Yes, more than two nulls. I hope we are talking about the same when referring "nulls". Take the following example:
Plaintext:
IHAVE NTGOT ACLUE
"Salted" Ciphertext (no substitition to keep it simple):
XIHAVE NTYGOT ACLUZE
The plaintext has been salted with some fake letters. The pattern is as follows:
*----- --*--- ----*-
Maybe it could be described as an "inverse grille". Before the ciphertext can be decrypted the fake letters have to be removed.
This kind of obfuscation does not necessarily break cycles because the substitution step is applied after putting in some fake letters. Maybe he added fake letters and avoided cyles. In this case I don’t have any idea how to detect these fake letters other than trying a lot of patterns. So I updated my python library by another test. You can draw some 17×20 monochrome bitmaps (patterns) and put them into a folder. My tool removes all letters from z340 which are matching black pixels and feed the resulting "cleaned" ciphers to the autosolvers.
I hope my gibberish is readable =)
Largo,
Yes, we are talking about nulls, meaning fake letters, the same.
My idea is that the 340 could be a route cipher, but we do not know the actual count of plaintext and some of the symbols are nulls. When we try to untranspose, the nulls create misalignments in the untransposed messages, making it impossible to solve.
Your message is not a transposition, but has nulls that make the message difficult to solve.
That gave me some ideas, including the possibility that if the 340 is a transposition cipher, the nulls could have been added during homophonic encoding instead of during transcription. Maybe it is possible to untranspose a route cipher with nulls, and detect them similar to how I am trying to detect the nulls in your message. I am working on that now and have a number of possible locations. It is an area of cryptography that I doubt has been fully explored. I have not looked at the solution, but will post a rough idea of where some of the nulls may be soon.
Hey Largo, sorry it took me so long to get back.
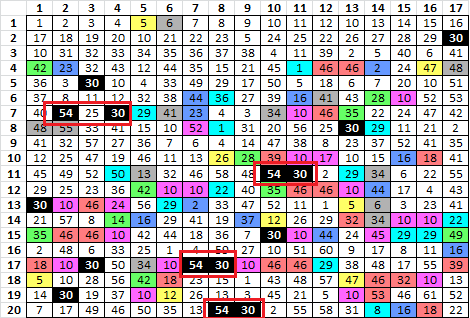
I tried a couple of different techniques to identify possible locations for your nulls. First, I looked at the period 1 repeats and the period 2 repeats to find situations where they had the same symbols. I also looked at the period 2 compared to period 3 repeats. For example, where the numbers are symbols:
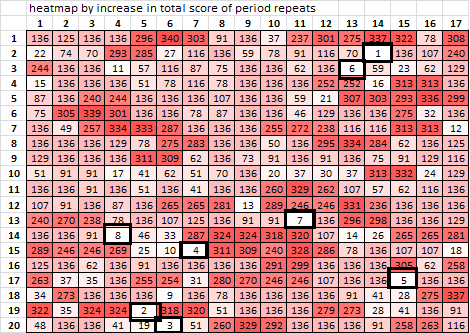
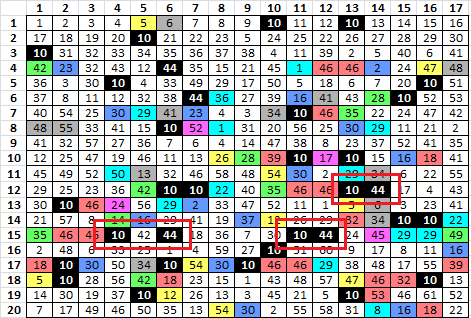
Then I applied my heatmap spreadsheet, which sometimes locates a null quite accurately for transposition messages. The numbers here are rank, or best possible locations for a possible null. There are many, and I marked only the top 8 or so:
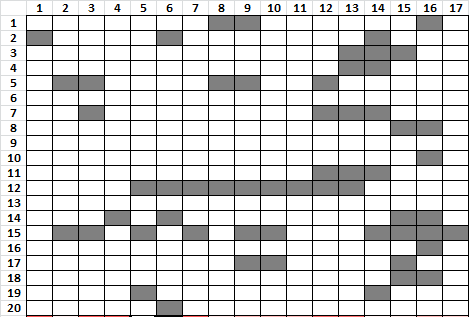
I could have applied the first technique in more detail, but felt that the probability of occurrence wasn’t high enough to mark all of them. Here is a rough estimate, and I think that some of the locations shaded are probably some of your null locations. But I could not detect any specific pattern:
Could you please show the null locations on this site, for future reference. Sometimes postings to images to other sites can be lost over time. Thanks.
Hey Largo, sorry it took me so long to get back.
Thats fine. There are so many other things to do rather than juggling 340 weird symbols ![]()
Thank you for checking my cipher with your tools. But I am still not sure if we are really talking about the same when speaking about "nulls" or "salts". My nulls are just random letters which I have placed before applying the homophonic substitution. How are you trying to detect them? I have no clue how to do that. Example:
Plaintext: MYNAMEISJOHNDOE Saltet plaintext: MYXNAMFEISJOPHNDOEA Plaintext and salts are separated: MY NAM EISJO HNDOE X F P A
How can X, F, P and A be detected even if they were within a pattern? When applying a homophonic substitution each symbol is "as good" as each other.
Here is the solution to the cipher posted before:
The attached image contains a pattern (17 x 20 pixels to resemble the cipher). The black pixels are marking letters which are just filler. When they are removed the cipher gets solved by AZDecrypt.
I have absolutely no idea how to detect such a pattern since the nulls are just random letters. How do they distinguish from the other letters?
BTW: I really like your heatmap. Have you ever created such a heatmap which shows the frequency of the symbols in z340? E.g. "+", "B", reversed "P" and so on are in dark red whereas the low frequency symbols are in light red?
Largo,
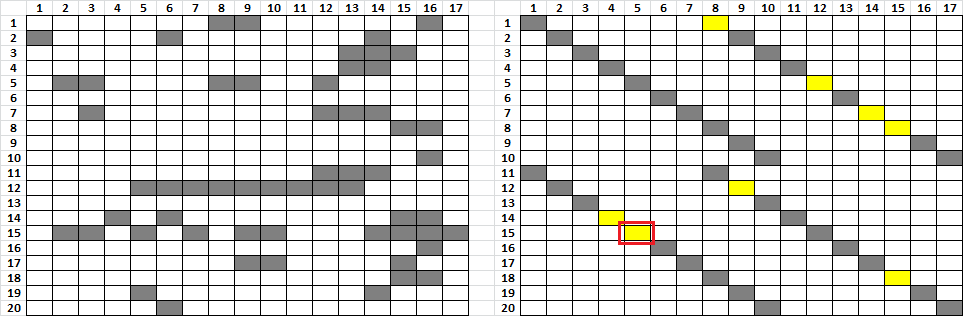
I don’t think that it is possible to detect all of the nulls in your pattern. I found a few:
And here is how I found one of them, for example marked in red. The numbers are your symbols converted to numbers for my spreadsheet. I found repeating period 1 bigram with symbols 10 – 44. And there was one period 2 bigram also with symbols 10 -44. I only checked about 1/3 of the period 1 repeats, the ones with lowest probability of occurrence. I suppose that I may have found a few more nulls if I checked them all.
Here is your heatmap. On the left is the Z340, with symbols converted to numbers. On the right are the count of those symbols, with highest count in dark red and lowest count in white:
Largo,
Here are some links to some discussions of skipped symbols and nulls for a route cipher:
viewtopic.php?f=81&t=2617&hilit=misalignment&start=350
viewtopic.php?f=81&t=2617&hilit=misalignment&start=440
viewtopic.php?f=81&t=2617&hilit=misalignment&start=540
viewtopic.php?f=81&t=2617&hilit=misalignment&start=610
viewtopic.php?f=81&t=2617&hilit=misalignment&start=620
Thank you for the heatmaps! Unfortunately there is definitively no pattern.
Also thank you for your explanation about your way to detect nulls. It never thought that it is possible to find any of them. I am sure I can learn even more from you in the future!
By the way: My python tools are able to take monochrome .png files (17×20 pixels) and remove letters from z340 at the positions of black pixels. Sometimes when I am not in the mood to implement new ideas I just draw patterns and feed the results to the autosolvers. Obviously without success ![]()
Now I will have a closer look at the links you have posted. Thanks for these!