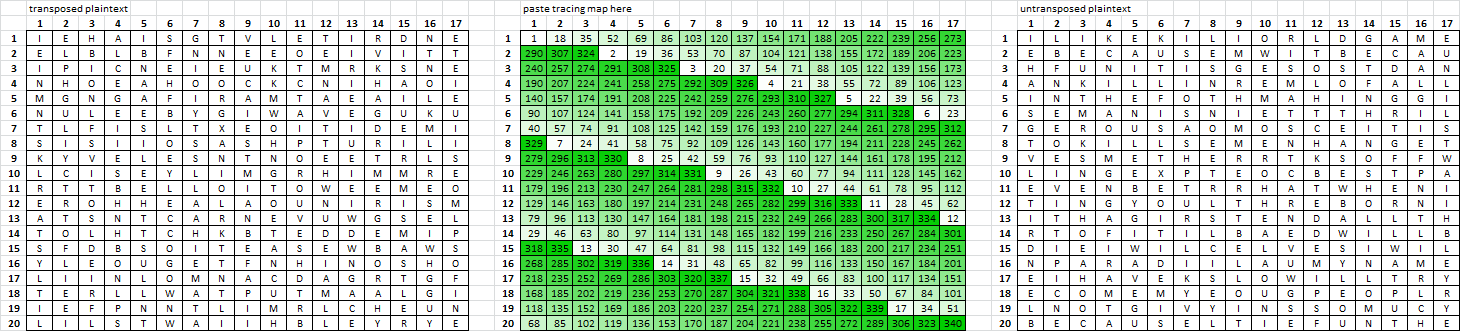
That’s very interesting. It is similar to the spikes I found a while back when I was playing around with different transposition schemes:
The noteworthy result from those experiments was that several high scoring AZDecrypt runs were due to operations involving "PeriodColumn(2) Period(18)" operations, which produced more repeating bigrams. Generally, AZdecrypt seems to score higher whenever repeating bigrams are high. Many combinations of operations are able to produce high numbers of repeating bigrams, so it’s hard to figure out which combination is correct.
I’ll add "PeriodColumn(2) Period(18)" to my list of things I need to check.
For clarification, there exists no bias in the code that makes AZdecrypt score higher when more bigrams are present in the cipher, I don’t think you meant to say that either. It’s still a bit of a guess as to why and to what extent it is happening but I believe it may have to do with bigrams being a plaintext property.
I am wondering if the various ways of getting AZDecrypt spikes at around 21000 are indications of being close to a real untransposition, or if those operations are truly false positives. If I recall correctly, an AZdecrypt spike of around 21000 is only about 1 sigma (1 standard deviation) away from the average of AZdecrypt runs on random shuffles of Z340.
It depends on how you get there. The problem is that some operations allow the cipher to be molded, especially with hill climbing or iterative processes. What I did in the follow up to main post of this thread was also include the reversed string, which always have the same bigram count. Observe, that the right side square does not have bright spots such as the left side square. So that seems to indicate direction. That’s a trick which can add weight.
Simple modifications allow more bigrams to be produced:
"PeriodColumn(2) Period(18) Swap(5, 105, 6, 1) Swap(101, 225, 3, 1)" produces 53 bigrams. Swap(5,105,6,1) exchanges a block of height 6 width 1 at position 5 with the same sized block at position 105. Swap(101,225,3,1) exchanges a block of height 3 width 1 at position 101 with the same sized block at position 225.
"PeriodColumn(2) Period(18) Swap(4, 104, 10, 1) SwapLinear(101, 238, 55)" produces 52 bigrams. SwapLinear(101, 238, 55) exchanges a substring of length 55 at position 101 with a substring of the same length at position 238.
"PeriodColumn(2) Period(18) RectangularSelection(7, 0, 7, 3) Period(10)" produces 52 bigrams. Period(10) is only applied to the RectangularSelection(7,0,7,3) which means a rectangular selection with upper left corner at row 7 column 0, and having height 7 and width 3.
I disagree that these are simple modifications. Given the arguments, the swap and rectangular selection allow for a truly immense amount of variations and your hill climber is stacking them. This basicly allows molding to some degree. The 340 can be configured up to 265 bigrams so you can increase all you want. Judging from the 408 I expect the 340 to come out at anywhere between 45 to 50 bigrams when correctly untranposed.
From a classical cryptology point of view I’m exploring a viable transposition hypothesis. The plaintext existed in a 23 by 15 grid and then was taken off by columns and transcribed into a 17 by 20 grid following either right-to-left, top-to-bottom or left-to-right, bottom-to-top. In that process some symbols were left out. I like it because it is a minimal hypothesis that can explain rare observations in the 340 such as pivots and periodical repeats (I understand that this hypothesis could be wrong and I would like to find out).
Or do you find "PeriodColumn(2) Period(18) Swap(5, 105, 6, 1) Swap(101, 225, 3, 1)" more viable?
I’ll add "PeriodColumn(2) Period(18)" to my list of things I need to check.
For clarification, there exists no bias in the code that makes AZdecrypt score higher when more bigrams are present in the cipher, I don’t think you meant to say that either. It’s still a bit of a guess as to why and to what extent it is happening but I believe it may have to do with bigrams being a plaintext property.
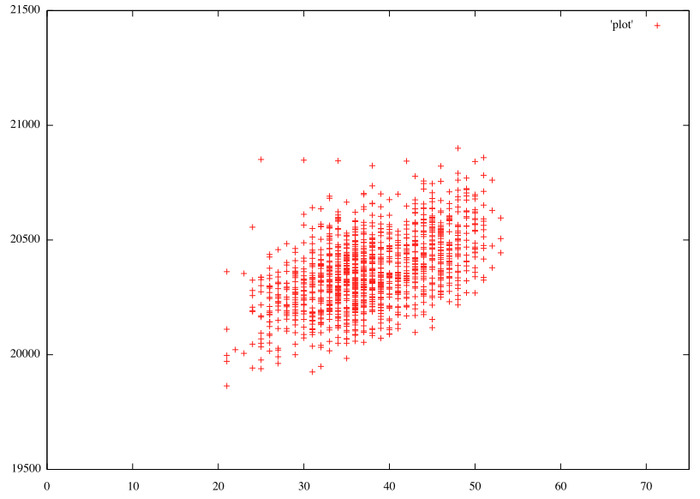
From my transposition experiments I produced the following plot of azdecrypt score vs # of repeating bigrams. It shows a cluster of scores that seems to drift upwards as the # of repeating bigrams increases.
Not sure how to interpret that – the scores still have a lot of variance, but the upwards drift is still detectable.
Also, "PeriodColumn(2) Swap(3, 156, 3, 3)" seems to greatly increase the L2 cycles (see item 5 here: http://zodiackillersite.com/viewtopic.php?p=43702 )
It depends on how you get there. The problem is that some operations allow the cipher to be molded, especially with hill climbing or iterative processes. What I did in the follow up to main post of this thread was also include the reversed string, which always have the same bigram count. Observe, that the right side square does not have bright spots such as the left side square. So that seems to indicate direction. That’s a trick which can add weight.
That’s a really nice plot. I like how you are using azdecrypt scores as a tool to prioritize candidates.
I disagree that these are simple modifications. Given the arguments, the swap and rectangular selection allow for a truly immense amount of variations and your hill climber is stacking them. This basicly allows molding to some degree. The 340 can be configured up to 265 bigrams so you can increase all you want. Judging from the 408 I expect the 340 to come out at anywhere between 45 to 50 bigrams when correctly untranposed.
From a classical cryptology point of view I’m exploring a viable transposition hypothesis. The plaintext existed in a 23 by 15 grid and then was taken off by columns and transcribed into a 17 by 20 grid following either right-to-left, top-to-bottom or left-to-right, bottom-to-top. In that process some symbols were left out. I like it because it is a minimal hypothesis that can explain rare observations in the 340 such as pivots and periodical repeats (I understand that this hypothesis could be wrong and I would like to find out).
Or do you find "PeriodColumn(2) Period(18) Swap(5, 105, 6, 1) Swap(101, 225, 3, 1)" more viable?
Not particularly; the goal of my transposition explorer was to discover transpositions that resulted in increased azdecrypt scores and increased bigram counts, while minimizing the number of transposition steps. I only report the results as a matter of reference rather than indicating a belief in a particular scheme. I agree that molding the cipher can give many paths to high bigram counts. But I think it’s compelling that "PeriodColumn(2) Period(18)" is all that’s needed to bring the bigram count up to 44. Is it a feature, or a phantom?
In the end, I got frustrated with that project, because there are too many possible schemes to rule out, without careful controlling it with test ciphers. I think you are right to focus on classical cryptology rather than strange homemade schemes, at least until all the classical schemes have been ruled out.
Jarlve, I did some work on this idea. See the third post down here: viewtopic.php?f=81&t=2617&start=1330
I spent some time on the 340 today. I have had some nagging issues about transposition, and one of them is whether a few transcription nulls, or transcription skips for the mirrored 340, could produce so many period 29 repeats and the pivots.
Here is the 340 mirrored, with period 29 repeat positions colored. 75 of the 170 positions in the bottom half are colored, which makes 44.1%. If the count of period 15 repeats is boson higgs significant, and the count of period 29 repeats astronomical, across the entire message, then what about just the bottom half? The pivots for the mirrored version are period 29.
period.29.mystery.1.png
period.29.mystery.1.png (34.65 KiB) Viewed 21 timesI made a spreadsheet suite to make period 15 messages, with an inscription rectangle of 22 columns x 15 rows and ten leftover, not transcribed plaintext at the end. Then I encoded with homophonic cycles, making about 25% of symbol selection random within cycle groups. Then I compared the messages with messages that had transcription skips introduced at random positions, with varying counts of transcription skips. For many of the messages, I limited the skips to the bottom half, and kept the count of skips to 4 or less. But I also tried a lot of variations.
For many of the messages with just a few skips, the count of period 15 repeats would drop slightly, and the count of period 29 repeats would increase slightly. But with no variation was I able to replicate a count of 65 period 29 repeats. Not even close. I could get 50 period 29 repeats with 3 skips, but getting more than that was difficult.
I am going to say that the null / skip idea for causing the pivots is probably not correct, and go back to the drawing board. I am still thinking that the message is some sort of transposition, but maybe he changed transcription direction for the bottom half, or did something else. There must be some sort of scheme that would make so many period 29 repeats, with 44.1% of the positions in the bottom half colored, and that must be what created the pivots.
It is not conclusive and I did not show all of my work. But with varying counts of randomly placed skips, some concentrated in the area of the pivots, I was not able to reproduce mirrored 340 period 29 stats.
Not sure how to interpret that – the scores still have a lot of variance, but the upwards drift is still detectable.
Also, "PeriodColumn(2) Swap(3, 156, 3, 3)" seems to greatly increase the L2 cycles (see item 5 here: http://zodiackillersite.com/viewtopic.php?p=43702 )
Yes, I remember these items. I’m incredibly skeptic that anything special happened during or after the encoding. My hypothesis is that Zodiac made a key, just like with the 408 but did not actively cycle the symbols as he did with the 408. Instead he took greater care not to repeat symbols in a given view window, which could have been the rows. It lines up with everything we know about the encoding. In that hypothesis increases you find to the cycles must be phantoms.
Not particularly; the goal of my transposition explorer was to discover transpositions that resulted in increased azdecrypt scores and increased bigram counts, while minimizing the number of transposition steps. I only report the results as a matter of reference rather than indicating a belief in a particular scheme. I agree that molding the cipher can give many paths to high bigram counts. But I think it’s compelling that "PeriodColumn(2) Period(18)" is all that’s needed to bring the bigram count up to 44. Is it a feature, or a phantom?
Given the increase I think it is more likely to be a feature.
In the end, I got frustrated with that project, because there are too many possible schemes to rule out, without careful controlling it with test ciphers. I think you are right to focus on classical cryptology rather than strange homemade schemes, at least until all the classical schemes have been ruled out.
You could use it to help us with the schemes we are exploring.
Jarlve, I did some work on this idea. See the third post down here: viewtopic.php?f=81&t=2617&start=1330
Okay, thanks for pointing that out. I’m going to take a look at it also. The basic question is if 1 to 5 nulls during transposition can be a likely cause for period 30 to shift to 29. Perhaps you are right and we need to move on to a more general question.
Does there exist some structure (any combination of symbols at any positions) in any step of the transposition process which causes period 29 bigrams repeats?
We have a couple of observations that link together:
– There are 2 pivotal structures in the 340 that are made up out of bigram 29 repeats.
– After mirroring the 340 there are 41 period 15 bigrams repeats and 34 period 29 repeats. A period shift from 30 to 29 is a real possibility due to some misalignment.
– A sharp increases of AZdecrypt scores (21000+) while adding a single new symbol in a contiguous region of about 15 characters wide (including other transposition steps). This contiguous region sits around one pivot.
– Period 30 bigrams repeats also increase while adding a single (or more) new symbol in the region around the pivot (position 200 give or take).
About the contiguous region and why it is important. If for instance a plaintext is transposed in a 23 by 15 grid. And the letters are taken off by columns and at one column one letter would be left out. Then you would find that to correct the misalignment, it would be valid to add a character over an entire region of about 15 characters wide. Because you just need to restore the length of the column (which is laid out horizontally after transposition) from 14 to 15. Another reason why I gave the original observation of this thread more weight.
Your findings concerning misalignments make me wonder if Zodiac applied irregular columnar transposition. In irregular columnar transposition, some columns have length L while others have length L-1. When the columns are then written out, the periodic bigrams would then be misaligned, possibly only by 1 position. Did you already explore that possibility? I think we talked about it before. I recall running some brute force searches of short keys to try to find peak bigram counts, fragments, and L=2 cycles. It may be very interesting to see with test ciphers how often period 29 pivots appear for irregular columnar transpositions of plaintext written in 15 or 30 columns.
Does there exist some structure (any combination of symbols at any positions) in any step of the transposition process which causes period 29 bigrams repeats?
Or alternatively, the transposition itself caused a misalignment. Mixing of periods or errors or for example skytale transposition does run into the same positions when the period number shares a divisor with the cipher length, but secondary rules can be added.
Your findings concerning misalignments make me wonder if Zodiac applied irregular columnar transposition. In irregular columnar transposition, some columns have length L while others have length L-1. When the columns are then written out, the periodic bigrams would then be misaligned, possibly only by 1 position. Did you already explore that possibility? I think we talked about it before. I recall running some brute force searches of short keys to try to find peak bigram counts, fragments, and L=2 cycles. It may be very interesting to see with test ciphers how often period 29 pivots appear for irregular columnar transpositions of plaintext written in 15 or 30 columns.
I haven’t fully explored that possibility. Irregular columnar transposition is the hypothesis I put forward.
The plaintext existed in a 23 by 15 grid and then was taken off by columns and transcribed into a 17 by 20 grid following either right-to-left, top-to-bottom or left-to-right, bottom-to-top. In that process some symbols were left out. I like it because it is a minimal hypothesis that can explain rare observations in the 340 such as pivots and periodical repeats (I understand that this hypothesis could be wrong and I would like to find out).
I would guess that the colums were taken off starting in either the upper-left or upper-right corner since that’s where the highest AZdecrypt scores are returned from. Important to note is that there is an input and output direction. Which smokie describes as inscription and transcription, which are concepts of classical cryptology. I believe Zodiac transcribed (output direction) from right-to-left, top-to-bottom or left-to-right, bottom-to-top and that’s why bigrams peak (41) after mirroring or flipping the 340.
I spent some time on the 340 today. I have had some nagging issues about transposition, and one of them is whether a few transcription nulls, or transcription skips for the mirrored 340, could produce so many period 29 repeats and the pivots.
I did the same thing with a 340 character part of the 408. After period 15 transposition it created 46 period 15 bigrams repeats and 38 period 30 bigrams repeats. Then any combination of 2 characters were removed and period 29, 30 and 31 bigream repeats were measured. Here is the graph, the left square is period 29, the middle square is period 30 and the right square is period 31. The x-axis is the first character removed from position 1 to 340 and the y-axis is the second character removed from position 1 to 339. The color brightness are the bigram repeat values where brighter is more.
There is more bright in the left square, which is period 29, indicating that removing characters does shift the period but with only 2 characters removed the effect is minor at best. The highest bigram repeats recorded for period 29 were 31. So that seems to confirm smokie’s results. If there is a structure misaligning period 30 into period 29 it must count quite a bit of characters. Interesting.

Yes to the post above. Maybe a structure and not just a few skips or nulls.
I have thought about this idea before. A 22 x 15 rectangle, except alternating 15 rows, then 14 rows, then 15 rows, etc. Period 1 would then be split between period 14 and period 15, and period 2 would become period 29.
However, when comparing the cross period bigram lists for all periods with period 15, I did not find a lot of period 14 bigrams that have symbols matching those of period 15 bigrams. The number is relatively low for period 14, at 67 ( red ). There are 99 bigrams with symbols that match period 15 bigrams at periods 16 and 26 ( blue ). The spike is not important because it is comparing period 15 with period 15.
Also, the potential for high count of period 15 repeats would be significantly diminished, so I don’t think that this is what he may have done. But maybe it is worth investigation.
Maybe the period 29 spike is possible with skips or nulls at regular intervals, but I don’t know.
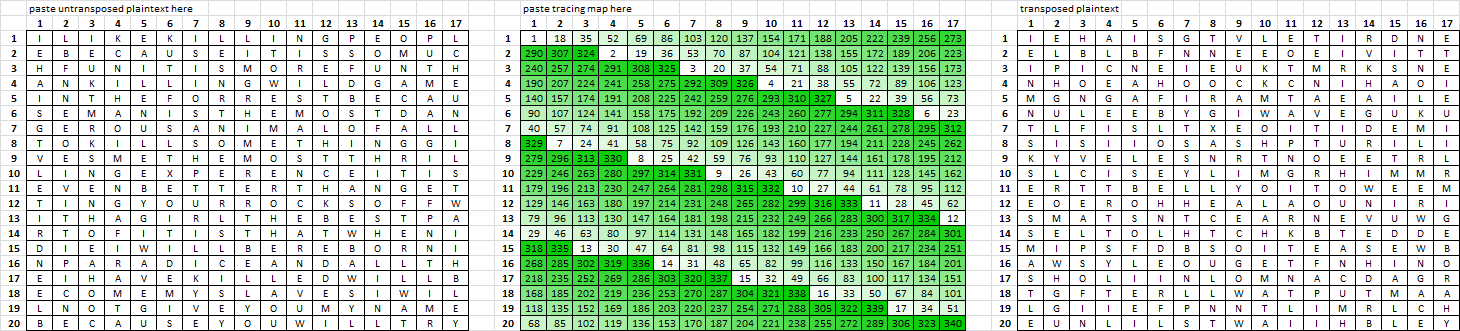
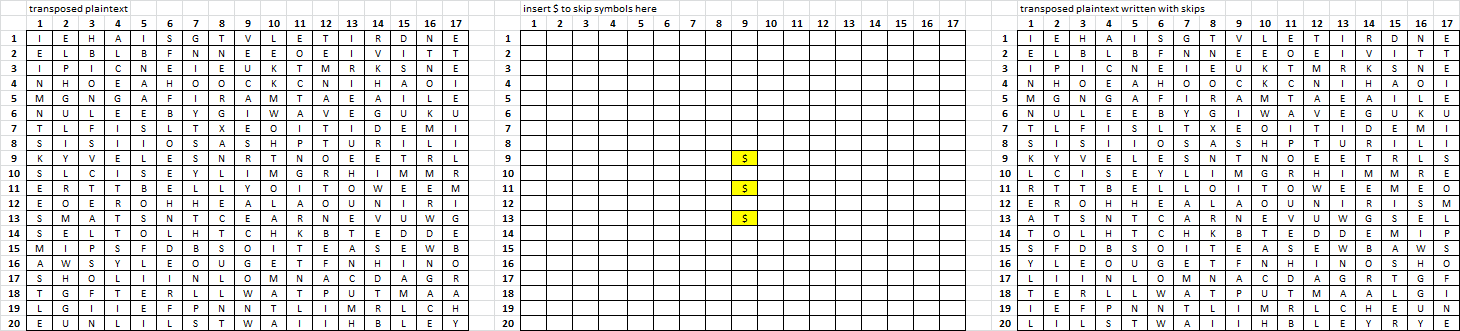
Here is an example of what three skipped plaintext will do to the readability of an untransposed message.
Very simple inscription rectangle 17 x 20, transcription rectangle 17 x 20. Inscription left right top bottom. Plaintext lifted from inscription rectangle top bottom left right. Transcription left right top bottom.
Skip three symbols in three locations in the area of the pivots ( although this would not create pivots ).
Untranspose. Message scroll to the right unreadable.
That is all it takes.
I L I K E K I L I O R L D G A M E
E B E C A U S E M W I T B E C A U
H F U N I T I S G E S O S T D A N
A N K I L L I N R E M L O F A L L
I N T H E F O T H M A H I N G G I
S E M A N I S N I E T T T H R I L
G E R O U S A O M O S C E I T I S
T O K I L L S E M E N H A N G E T
V E S M E T H E R R T K S O F F W
L I N G E X P T E O C B E S T P A
E V E N B E T R R H A T W H E N I
T I N G Y O U L T H R E B O R N I
I T H A G I R S T E N D A L L T H
R T O F I T I L B A E D W I L L B
D I E I W I L C E L V E S I W I L
N P A R A D I I L A U M Y N A M E
E I H A V E K S L O W I L L T R Y
E C O M E M Y E O U G P E O P L R
L N O T G I V Y I N S S O M U C Y
B E C A U S E L T I E F U N T H E
I have thought about this idea before. A 22 x 15 rectangle, except alternating 15 rows, then 14 rows, then 15 rows, etc. Period 1 would then be split between period 14 and period 15, and period 2 would become period 29.
I replicated your idea.
I took the 408 (because it has many period 2 bigram repeats) and set it in a 23 by 15 grid and alternated the length of each column. Then took off the cipher by columns starting in the upper-left corner and set it in a 17 by 20 grid. Since the length of each column was alternated (15,14,15,14,…) the cipher length reduces from 345 to 334.
Graph: period(1-334) versus bigram repeats. The peak you see is period 29, it counts 36 bigram repeats. I find it interesting that mixing periods can create a "fake" period.

Combinations processed: 334/334 Measurements: - Summed: 5896 - Average: 17.65269461077844 - Lowest: 8 (Period(UTP,134)) - Highest: 36 (Period(UTP,29)) 9FQ^IQKR8MOccW%6 YL)SqN6RlPE+P9DM6 #p(HUN^/@Z/H5ZqBI eItA=99ZP)JXL)E9% )S%AG/@Sd8dWUDLZr %9UK(r5/qHR)(lZBK B!/zP!k_NPff%%q9 pS#8FTVzUAO_kY#F( B5ZYEUePTOeBHR@Lc rKp6#5YRMPVNXMpH k7BR=JOWtqrOd=ADV U9pYReIE9VeG9zpcX ^A8YH#W/r#Ge+#=UU YEMBI@IB%X_BI%@lU P5X!V%qdtWkf+O^D+ JJWIWYV7Rq8RRtQk MqqH+qlGqR+LA5+N_ _eTqDGkj)P9VkF^FG tE9Bc=l58T)#SYNkK TZ6^MLtS8qX
Here is an example of what three skipped plaintext will do to the readability of an untransposed message.
From my testing it takes only 2 characters, depending on their positions.
I’ve tested the 340 with up to 2 characters added at any positions in any of the 4 period 15 directions. The results are that scores increase quite a bit (up to 21300+) with a visible bias for 2 of the 4 directions (normal and flipped). I did a few iterative runs and saw that after 2 characters were added, scores do not increase as much.
Mirrored 340, period 15 untransposed:
0 character(s) added: 20500+
1 character(s) added: 21000+
2 character(s) added: 21300+
3 character(s) added: 21400+
It makes me skeptic of a finding a structure. And think it is more likely that the misalignment is part of the transposition itself, though a character may still have been skipped. Complicated, I would say it is to early to rule out a structure.
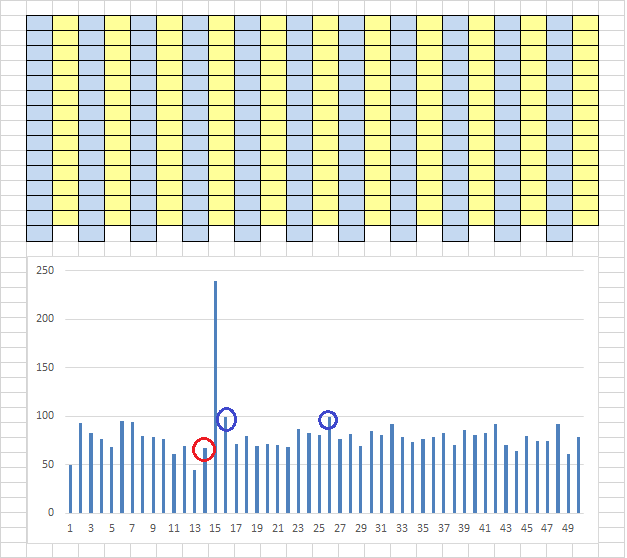
I’ve put forward a test cipher in this thread that has 5 skipped characters. Here’s what it looks like when I perform the test that looks for skipped characters (the same test as main post).
It shows at least 3 peaks. That are 3 out of the 5 skipped characters. So the question is, if a multitude of characters have been skipped in the 340, why is there only one peak? My thinking is that only 1 character was skipped (transcription error? or would appear to be skipped?) and the misalignment exists in the transposition itself.
Jarlve:

340:

I’ve put forward a test cipher in this thread that has 5 skipped characters. Here’s what it looks like when I perform the test that looks for skipped characters (the same test as main post).
It shows at least 3 peaks. That are 3 out of the 5 skipped characters. So the question is, if a multitude of characters have been skipped in the 340, why is there only one peak? My thinking is that only 1 character was skipped (transcription error? or would appear to be skipped?) and the misalignment exists in the transposition itself.
Jarlve:
340:
I really like your idea of using AZD to detect skip positions. It appears to be a very useful tool, and shows that replacement of a skip does not have to be the exact same position to re-align the message enough to affect AZD ability to get an improved solution.
Not sure about interpreting the graph for the 340. There are a lot of ways to create period 15 bigram repeats other than using just one inscription rectangle and on transcription rectangle.
I have half a mind to try something like this:
It would increase the count of period 15 repeats, and move the period 29 repeats to the bottom half of the message. It is easy for me to imagine him doing something like that. But before doing so I would have to compare the list of period 29 bigrams to the list of period 30 bigrams to see if they are similar. I have added that to my to do list.