I did not expect to find a link between the encoding and the pivots but here it seems to be. After formatting the 340 in a 10 by 34 grid and removing any combinations of 2 rows, removing exactly the 2 rows that hold the horizontal part of the pivots gives the highest returning encoding score.

It chimes in with the general direction of the thread; that there exists some disruptive structure in the 340 in the form of left out characters, randomization, nulls/filler, transposition errors, transposition overlapping, transposition with special rules or a combination thereof.

Here is a compilation image of perhaps related phenomena:
– All highlighted squares are period 29 bigram repeats of which there are a substantial amount (after mirroring the 340).
– Highlighted in green are the pivots which also happen to be period 29 bigram repeats. Period 29 could possibly have shifted from period 30 with period 15 as the main direction.
– The red line indicates where a larger physical gap between the rows in the 340 can be observed.

Can anyone spot other interesting stuff?

As stated, the test is scoring the encoding. Which is my 2 symbol cycles measurement and another thing added.

OK – I’m familiar with the L2 cycles measurement but what is the "another thing"? Maybe you already explained it and I missed it. I need to re-read much of this thread! Very interesting stuff!

The red line indicates where a larger physical gap between the rows in the 340 can be observed.

I had forgotten about your previous analysis of the gaps between rows: viewtopic.php?p=26650#p26650

Can anyone spot other interesting stuff?

– The gap occurs between rows 12 and 13. Lines 11, 12 and 13 each have no repeating symbols in them (same is true of lines 1, 2 and 3).
– The number of rows after the gap is 8, which is the same row size of each of the 3 separate sections of Z408.
– Each box corner pattern occurs in exactly one column to the right of each pivot.

As stated, the test is scoring the encoding. Which is my 2 symbol cycles measurement and another thing added.

OK – I’m familiar with the L2 cycles measurement but what is the "another thing"? Maybe you already explained it and I missed it. I need to re-read much of this thread! Very interesting stuff!

The other thing sums the positions of the first occurance of every unique symbol (lower is better). Something I use to differentiate between a normal and reversed string, since encoding scores are the same on these. It doesn’t change much in this case.

AZdecrypt combine statistics for: 340.txt
--------------------------------------------------
Normal: 2924
Mirror: 2936
Flip: 3589
Reverse: 3525
Columnar(UTP,1): 4090
Columnar(UTP,2): 3956
Columnar(UTP,3): 4033
Columnar(UTP,4): 4012
Diagonal(UTP,1): 3486
Diagonal(UTP,2): 3601
Diagonal(UTP,3): 3647
Diagonal(UTP,4): 3616
Diagonal(UTP,5): 3431
Diagonal(UTP,6): 3471
Diagonal(UTP,7): 3817
Diagonal(UTP,8): 3741
--------------------------------------------------
Combinations processed: 16/16
Measurements:
- Summed: 57875
- Average: 3617.1875
- Lowest: 2924 (Normal)
- Highest: 4090 (Columnar(UTP,1))

A few pages back I mentioned a repeating bigram structure I found in the 408 @ period 10. To clarify, these show up on periodical bigram maps. A periodical bigram map shows the location of each bigram repeat at a certain period in a set of dimensions. What I would describe as a repeating bigram structure (RBS) is a structure that shows up on such bigram maps that partially repeats itself at a given offset (ignoring the symbols, each map position is either 0 or 1).

Note that I have not come up with a statistic or algorithm to detect these, it was found by accident. Here’s the image for the 408 again from a few pages back.

So how does this work? Is it something simple I am not seeing? My current hypothesis for this phenomenon (RBS) is that it comes into existance as some kind of harmonic between the plaintext, encoding, grid dimensions and period. I wonder if we can use it somehow to gather more intelligence about the ciphers.

Now, I didn’t plan this to happen. But I was looking at the image I compiled of the 340 @ period 29 a couple of posts up and it hit me, it’s the same thing I found in the 408. The pivots are part of a repeating bigram structure (RBS). And possibly, all the strange repeating stuff we spotted in the 340 are essentialy part of RBS under different periods and alignments. The pivots can then be described as an artifact between the interaction of the RBS and increased amount of bigram repeats at period 29.

Here is the mirrored 340 period 29 bigram map (unmirrored after) with on the left and right side the pivots offset on eachother to show the repeats. I would also suggest that you take a close look at my compilation image of the 340 a couple of posts up to correlate the positions.

Back to the encoding and possible connection to the pivots. I ran a test that removes characters sliding through the cipher from start to end, so that it finds the most optimal fragment to remove according to the encoding measurement. A peak occurs at a length of 17 (characters removed) at position 224. These characters are "N^f524b.cV4t++yBX" which include the second pivot. For lower lengths, the position at which it finds the optimal fragment switch between the horizontal part of the first and second pivot.

Encoding score, characters removed, position
--------------------------------------------------------
340 base score: 2152.181258812112

1: 2186.622688218925 (Remove characters(1,95))
2: 2200.258546616776 (Remove characters(2,212))
3: 2215.244518697215 (Remove characters(3,212))
4: 2226.895464641129 (Remove characters(4,212))
5: 2234.013330146504 (Remove characters(5,212))
6: 2241.610075363423 (Remove characters(6,230))
7: 2241.782472555693 (Remove characters(7,211))
8: 2246.645053645351 (Remove characters(8,228))
9: 2246.004685025064 (Remove characters(9,227))
10: 2247.611131850579 (Remove characters(10,230))
11: 2262.213369051972 (Remove characters(11,225))
12: 2267.803661341454 (Remove characters(12,224))
13: 2272.54644418709 (Remove characters(13,224))
14: 2274.270810970042 (Remove characters(14,224))
15: 2283.105462180183 (Remove characters(15,225))
16: 2289.692724332181 (Remove characters(16,225))
17: 2294.802438277315 (Remove characters(17,224)) <---
18: 2277.164021758586 (Remove characters(18,223))
19: 2269.63275525172 (Remove characters(19,222))
20: 2268.131054722815 (Remove characters(20,221))
21: 2245.220926163916 (Remove characters(21,280))
22: 2238.596107443316 (Remove characters(22,280))
23: 2257.344271317202 (Remove characters(23,280))
24: 2237.854406140045 (Remove characters(24,279))
25: 2230.821338786619 (Remove characters(25,278))
26: 2206.65695284901 (Remove characters(26,274))
27: 2216.799656885151 (Remove characters(27,274))
28: 2225.331879386287 (Remove characters(28,280))
29: 2214.007253783215 (Remove characters(29,166))
30: 2209.742488278937 (Remove characters(30,188))
31: 2208.32570411336 (Remove characters(31,187))
32: 2204.336562554167 (Remove characters(32,186))
33: 2188.012581440303 (Remove characters(33,185))

The pivots are part of a large repeating structure made up out of period 29 repeats.

Here’s another view of the repeating structure I found in the mirrored 340 @ period 29. Basicly this map shows the period 29 bigram repeats and in it a large structure repeats itself at least 2 times at a specific offset x=5, y=2 or period 29. This is very interesting because the pivots are part of this structure.

I colored it in manually and the shape of the structure is my interpretation, a few other interpretations should be possible because the structure overlaps here and there. The orange and red squares repeat perfectly at the given offset and form the main shape of the structure. The yellow and purple squares are the start of 2 more structures (based off the main structure) and the blue squares did not meet my criteria but some of them do repeat here and there. I did not wrap around the cipher. It also happens in the 408 at period 10.

Consider that this observation, if well understood, may explain the formation of the pivots.

Hi Jarlve,

this is an very intersting find. I can see that the orange and red squares form a structure, but I find it a bit hard to see the relationship between the structure and the bigrams in the image. When I apply period 29 to the z340 I count 33 bigram repeats, can you confirm that?

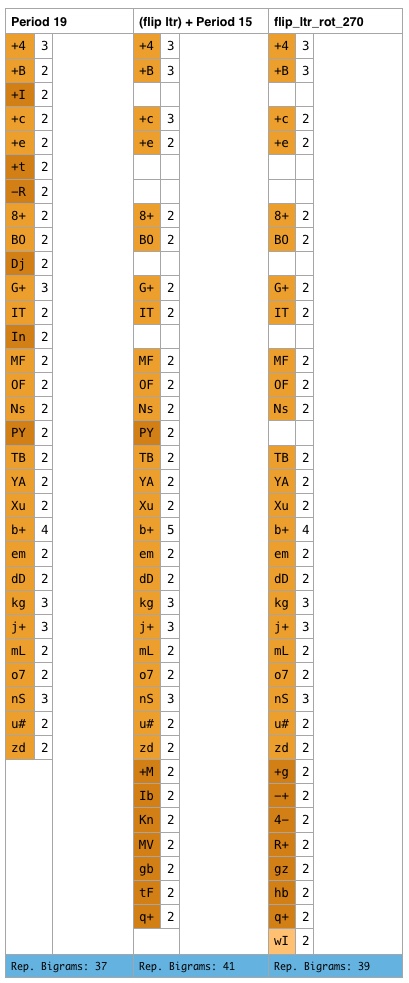
Today I fooled around a bit with period 19 / flipped period 15 and had an idea. What would happen when I shift the rows of the cipher by an offset of -2 per row? Row 1 has no offset, row 2 will then be shifted 2 letters to the left, row 3 will be shifted 4 letters to the left…and so on. This array represents the offsets for the shifting:
shifting_pattern = _list([0, -2, -4, -6, -8, -10, -12, -14, -16, 0, -2, -4, -6, -8, -10, -12, -14, -16, 0, -2]),

After the row shift I rotated the cipher by 270 degrees (respectively -90 degrees). Then I counted the repeated bigrams and found 39. This is nothing special since this kind of transposition has almost the same effect like a period 19 transposition. The only difference is that period 19 is consistent over the whole cipher and my row shift creates two „breaks“ (I hope you can decipher my broken english…I am still a bit tired from the new years party last night).
So I think that a regular shifting pattern can result in a cipher which looks like a cipher with a misalignment.

H+MwICV9K-RR+4apIbID
EB+o7emLhu5JN0VMq+FH
RjUVFFuznc7IImUQL+eN
akZxPaLjMU1o7tZGRqhb
bOGb+gIG+VE7FV7gtWWe
clWO3Dkg0+ITB4-ITCnS
dDj+4j7J+dD4t1+t+uvu
VWq+eb+pZJYMj+rmLW1Z
PYLR5wK2R+Bm8+BxftBO
emkKyRQkgOb+wcXu#Pyw
InugzdlOFb03RGfBCOYA
foHSMF8+BvTBuFoKnSOI
LKJb+cgytnMF#Nsj+HBK
TpBbuOUNrFKgzd4OFTo8
Gqrv1-tYABOnSpzbc5-+
gNsd2oXu#rUtr7CdWjCa
hbtchhG+4-+ckgEmBqtM

Jarlve, smokie, David…….Do you think that could be the case? Maybe I missunderstand something…

The following sheet shows the differences between the repeated bigrams for period 19, flipped left to right + period 15 and shifted rows. I have used my own transcription of 340, so the symbols will not match with yours:

Hi largo.. A long time ago I spent many days on column and row shifts and found the easiest way to bring the period 19 repeats into play was the row shift x2 positions as you explained but could never get any decent solves. The other way was scytale .. Nothing good found in that lot either. The other way was break up columns into odds and evens and then move up each column X one and then knit odds and evens together.. Nothing much in that…but I do like that whole simplistic method of z making the 340 difficult using such a method..

Hi Jarlve,

this is an very intersting find. I can see that the orange and red squares form a structure, but I find it a bit hard to see the relationship between the structure and the bigrams in the image. When I apply period 29 to the z340 I count 33 bigram repeats, can you confirm that?

Hey Largo,

It are 34 bigrams at period 29 after mirroring the 340.

That is the right question, what is the relation, what is going on here? I don’t understand it either, perhaps we are missing a simple fact. Here’s an image of the 408 with the same thing at period 10.

Today I fooled around a bit with period 19 / flipped period 15 and had an idea. What would happen when I shift the rows of the cipher by an offset of -2 per row? Row 1 has no offset, row 2 will then be shifted 2 letters to the left, row 3 will be shifted 4 letters to the left…and so on. This array represents the offsets for the shifting:
shifting_pattern = _list([0, -2, -4, -6, -8, -10, -12, -14, -16, 0, -2, -4, -6, -8, -10, -12, -14, -16, 0, -2]),

After the row shift I rotated the cipher by 270 degrees (respectively -90 degrees). Then I counted the repeated bigrams and found 39. This is nothing special since this kind of transposition has almost the same effect like a period 19 transposition. The only difference is that period 19 is consistent over the whole cipher and my row shift creates two „breaks“ (I hope you can decipher my broken english…I am still a bit tired from the new years party last night).
So I think that a regular shifting pattern can result in a cipher which looks like a cipher with a misalignment.

Mr lowe did that with columns, as he mentioned. I like your idea but how would Zodiac have transposed it then? That seems a bit strange.

Hi Jarlve,

this is an very intersting find. I can see that the orange and red squares form a structure, but I find it a bit hard to see the relationship between the structure and the bigrams in the image. When I apply period 29 to the z340 I count 33 bigram repeats, can you confirm that?

Today I fooled around a bit with period 19 / flipped period 15 and had an idea. What would happen when I shift the rows of the cipher by an offset of -2 per row? Row 1 has no offset, row 2 will then be shifted 2 letters to the left, row 3 will be shifted 4 letters to the left…and so on. This array represents the offsets for the shifting:
shifting_pattern = _list([0, -2, -4, -6, -8, -10, -12, -14, -16, 0, -2, -4, -6, -8, -10, -12, -14, -16, 0, -2]),

After the row shift I rotated the cipher by 270 degrees (respectively -90 degrees). Then I counted the repeated bigrams and found 39. This is nothing special since this kind of transposition has almost the same effect like a period 19 transposition. The only difference is that period 19 is consistent over the whole cipher and my row shift creates two „breaks“ (I hope you can decipher my broken english…I am still a bit tired from the new years party last night).
So I think that a regular shifting pattern can result in a cipher which looks like a cipher with a misalignment.

H+MwICV9K-RR+4apIbID
EB+o7emLhu5JN0VMq+FH
RjUVFFuznc7IImUQL+eN
akZxPaLjMU1o7tZGRqhb
bOGb+gIG+VE7FV7gtWWe
clWO3Dkg0+ITB4-ITCnS
dDj+4j7J+dD4t1+t+uvu
VWq+eb+pZJYMj+rmLW1Z
PYLR5wK2R+Bm8+BxftBO
emkKyRQkgOb+wcXu#Pyw
InugzdlOFb03RGfBCOYA
foHSMF8+BvTBuFoKnSOI
LKJb+cgytnMF#Nsj+HBK
TpBbuOUNrFKgzd4OFTo8
Gqrv1-tYABOnSpzbc5-+
gNsd2oXu#rUtr7CdWjCa
hbtchhG+4-+ckgEmBqtM

Jarlve, smokie, David…….Do you think that could be the case? Maybe I missunderstand something…

The following sheet shows the differences between the repeated bigrams for period 19, flipped left to right + period 15 and shifted rows. I have used my own transcription of 340, so the symbols will not match with yours:

I am not really sure. It looks like the message above is 20 x 17. You redrafted the message into 19 columns, then rotated it so that the repeat symbols would be read horizontally, and then redrafted it again into 20 columns?

Jarlve.. It’s very visually symmetrical its as if you could fold it and join it together like a mad magazine fold in. Do you remember them.. Which reminds me
AlfrEdEnEuman..13 letters haha..

That is the right question, what is the relation, what is going on here? I don’t understand it either, perhaps we are missing a simple fact. Here’s an image of the 408 with the same thing at period 10.

I’m confused about the significance of this. Wouldn’t any period N bigram repeats form repeating structures by definition when you mark them in the original cipher text? Each part of the bigram you highlight would always be 10 positions apart, for example, when looking at period 10 bigrams. It is like making a drawing with a pen that is attached to a rigid rod and another pen, where movements of the 1st pen create an equal image via the 2nd pen but offset a bit from the 1st pen’s markings. Am I missing something?

I’m confused about the significance of this. Wouldn’t any period N bigram repeats form repeating structures by definition when you mark them in the original cipher text? Each part of the bigram you highlight would always be 10 positions apart, for example, when looking at period 10 bigrams. It is like making a drawing with a pen that is attached to a rigid rod and another pen, where movements of the 1st pen create an equal image via the 2nd pen but offset a bit from the 1st pen’s markings. Am I missing something?

Hey doranchak,

If you look at the image of the 408, the red squares are the start of each bigram repeat, and the orange squares are the end. What’s special here is the regionality. If you look at the top-left square (the "9", blue one), it is a bigram that starts there and repeats 10 squares later (to the left). It does not share the regionality of the red structure. It seems that some of the periods are on another period so to say. I wonder if there is anything we could infer from this rather than it being some sort of harmonic between the cipher plaintext, encoding, period and physical dimensions.

If you look at the image of the 340, the orange squares are the start of each bigram repeat, and the red squares are the end. Again there is strong regionality here, with hints of up to 4 structural repeats (period on period). It is indicative that the pivots owe their existance to this phenomena. We are getting tantalizingly close to explaning the pivots.

OK – so you are highlighting clusters where bigrams tend to start and end. Is that right?