I just did a test to check my assumption for the strange cycle behavior of z340 ("interlocked cipher"). If there are interspersed symbols in z340 that do not belong to the LTRB order, then it may be possible to identify them using a genetic algorithm. The first test was an ideal happy sunshine case:
0ABCDEFABCDEFABCD E1FABCDEFABCDEFAB CD2EFABCDEFABCDEF ABC3DEFABCDEFABCD EFAB4CDEFABCDEFAB CDEFA5BCDEFABCDEF ABCDEF6ABCDEFABCD EFABCDE7FABCDEFAB CDEFABCD8EFABCDEF ABCDEFABC9DEFABCD EFABCDEFAB0CDEFAB CDEFABCDEFA1BCDEF ABCDEFABCDEF2ABCD EFABCDEFABCDE3FAB CDEFABCDEFABCD4EF ABCDEFABCDEFABC5D EFABCDEFABCDEFAB6 7CDEFABCDEFABCDEF A8BCDEFABCDEFABCD EF9ABCDEFABCDEFAB
In this cipher there is a perfect order of ABCDEF, which was interrupted once in each line by a different symbol (0-9). My genetic algorithm has identified the pattern in about 50 generations. As fitness function the 2-Cycle-Score from Jarlve was used.
Next I took the first 320 characters of z408 (16×20) and substituted them 100% cyclically. Then I inserted an additional symbol in each line to interrupt the cycle.
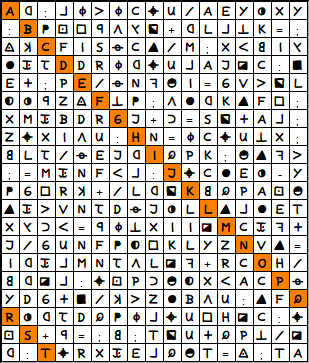
First 320 letters from z408, 16×20
h:cjajCuU5AEYxXY :39ybdro+hLc1K=; veFISqCw5M;Xn0Ir 7s2DRjhuUcAJlC:k Ei;P5qNpgI=GVaoL 4xbZv13;d7hKwFy; XMsBDRJ+t=SoiAc; ZuXIdU:N=jCuU1X; 0L25qEJhQPK;gwpa ;=MsNFnc:uC7Ex-Y 3GyRe+5Lho0QPA9g wsaVN2DqJxLwc7ET Xrtn=bj1XIIlCspi J5GUNF34yKLYZVw= IhscMN2dLlp+RCH5 0hlc:u9Ptg4XnACq YDGik5eaZ7BdU:wF xh2DQ3jcuUyHlC:u 9+b=;0;ToUiQP15l h:uRXsEcQgT=v;TA
Added 20 Nulls (one per row)
Ah:cjajCuU5AEYxXY :B39ybdro+hLc1K=; veCFISqCw5M;Xn0Ir 7s2DDRjhuUcAJlC:k Ei;PE5qNpgI=GVaoL 4xbZvF13;d7hKwFy; XMsBDRGJ+t=SoiAc; ZuXIdU:HN=jCuU1X; 0L25qEJhIQPK;gwpa ;=MsNFnc:JuC7Ex-Y 3GyRe+5LhoK0QPA9g wsaVN2DqJxLLwc7ET Xrtn=bj1XIIlMCspi J5GUNF34yKLYZNVw= IhscMN2dLlp+RCOH5 0hlc:u9Ptg4XnACPq YDGik5eaZ7BdU:wFQ Rxh2DQ3jcuUyHlC:u 9S+b=;0;ToUiQP15l h:TuRXsEcQgT=v;TA
On this picture you can see more clearly what is meant:
The 16×20 cipher has a 2-symbols cycling score of 3706. After inserting the nulls the score is 3426. Now I ran my genetic algorithm again. After only 47 generations a score of 4045 was reached. This is significantly higher than the score of the perfect cyclic cipher.
Conclusion:
It does not seem possible to identify interspersed symbols within a homophonic substitution in this way. A perfect cyclic cipher does not generate the maximum reachable score of the 2 symbol cycle scoring. So a different approach would be needed here. Can anyone think of a better solution? Or does someone see an obvious error in my analysis?
Translated with http://www.DeepL.com/Translator
Hey Largo,
Your first text is perfect except for the nulls, so it is possible to find and be sure of the nulls since changes to all the other symbols cannot improve things. "ABCABCABC" is perfect. With sequential homophonic substitution ciphers, even when they are "perfectly cyclic", they are not perfect as in your first text and all sort of improvements are possible. This then becomes a big deal with a very large search space. Either decrease the search space or use a stronger statistic. Imagine trying to find a transposition while allowing all 340 symbols to be swapped or uniquely rearranged, the statistic would always fall short.
As a strict homophone substitution believer I’d say:
"Of course does the cipher behave differently if you add additional symbols/homophones".
It then automatically should get a higher or lower score. ‘Higher’ could be accidential or, by adding symbols in each line, due to strengthening the overall sequential character of the cipher.
QT
*ZODIACHRONOLOGY*
With sequential homophonic substitution ciphers, even when they are "perfectly cyclic", they are not perfect as in your first text and all sort of improvements are possible.
Thank you for the explanation. This confirms my assumption that in this way it is impossible to find the positions of the nulls. If there is a null per line, then there are 17 possible positions per line. With 20 lines this makes 17^20 = 4.064.231.406.647.572.522.401.601 possibilities. In addition, it is even quite easy to sort the symbols "by hand" so that a better score is achieved.
As a strict homophone substitution believer I’d say:
"Of course does the cipher behave differently if you add additional symbols/homophones".
Even if z340 is a pure homophonic substitution, there must be a reason for the interrupted cycles, no? If we could find the locations where the cycles are interrupted, we would be one step further in any case (whether pure homophonic substitution, underlying transposition or interlocked cipher). Pity it doesn’t work with my approach.
Translated with http://www.DeepL.com/Translator
Even if z340 is a pure homophonic substitution, there must be a reason for the interrupted cycles, no? If we could find the locations where the cycles are interrupted, we would be one step further in any case.
That is correct.
The following two symbols, for example, could both represent the same (frequent) letter (‘w’ and some type of filled out ‘circle’). They only occur in the first/last vs. the middle part of the cipher and may or may not belong together. The ‘w’ symbol (here represented by ‘A’) even occurs four times in a string of moreless 27 symbols (14.8%; line 17 -19). Except occurring once in line 2 and line 3 it does not occur anywhere else.
Each letter has either one or a group of homophone(s). Which homophone is actually selected depends on both, the encryption process as well as the actual cleartext (if there is only two K in the cleartext, the homophone won’t be used until the letter occurs). The encryptor can either choose a sequence, shuffle the homophones or use a group of homophones for certain parts of the cipher.
The previous can also vary for each letter (and most likely does). It is questionable if Z had used any solid ‘system’ in this cipher. Even in the 408, although using sequences, he got mixed up with those sequences towards the end of the cipher.
I always asked myself why that happened but I guess he either wanted to complicate the cipher more or simply got confused during the set-up of the cipher. When ‘creating’ the 340, he already had known about it being complicated to keep up the sequences for ~20 letters simultaneously..so he discarded the sequences and rather used ‘areas’ where he used the homophones. This, however, is not always the case…some homophones occur at almost any part of the cipher (e.g. the + symbol).
QT
*ZODIACHRONOLOGY*
Even if z340 is a pure homophonic substitution, there must be a reason for the interrupted cycles, no? If we could find the locations where the cycles are interrupted, we would be one step further in any case (whether pure homophonic substitution, underlying transposition or interlocked cipher). Pity it doesn’t work with my approach.
The problem is that we cannot even say that the cycles are interrupted though that is one possibility. We need to formulate some hypotheses for the 340 being less cyclic than the 408 and then see if we can distinguish between them. Do that before assuming nulls imo.
The problem is that we cannot even say that the cycles are interrupted though that is one possibility. We need to formulate some hypotheses for the 340 being less cyclic than the 408 and then see if we can distinguish between them. Do that before assuming nulls imo.
I expressed myself somewhat misleadingly. I don’t necessarily mean "nulls" in the sense of blenders. These "nulls" can just as well be interlocked ciphers. Like the example linked by doranchak:
viewtopic.php?f=81&t=3982&start=60#p64819
My test was not based on any particular assumption. Rather, it was about finding the positions where a cycle is interrupted (if that applies at all to z340, as you just mentioned).
To compare, the 408 (all n-gram symbols marked blue):
click to see full picture
QT
*ZODIACHRONOLOGY*
The encryptor can either choose a sequence, shuffle the homophones or use a group of homophones for certain parts of the cipher.
…
When ‘creating’ the 340, he already had known about it being complicated to keep up the sequences for ~20 letters simultaneously..so he discarded the sequences and rather used ‘areas’ where he used the homophones. This, however, is not always the case…some homophones occur at almost any part of the cipher (e.g. the + symbol).
In my opinion, there are many possible explanations for the distribution of homophones. If the plaintext uses unusual words, this is also reflected in the substitution. Such phenomena can also occur if the key does not really match the actual letter frequency of the plaintext. Another possibility would be that several keys were used or the key was rotated after n letters. A transposition can be the reason too.
For example, if you take a book from Projekt Gutenberg and create thousands of ciphers (always in 340 sizes, start position plus 1), you will always get strange examples with strange statistics. If you then look at the plain text, you can usually see the reason for the strange behavior.
Deciphering a homophonic substitution is only made more difficult by variable cycles if one tries to solve the cipher manually. Current solvers have no problem with this and even completely random cycles are no challenge. I don’t want to categorically rule out that 340 is an LRTB substitution like z408, but I’m extremely skeptical about that. In fact, if there is no transposition, different keys or other additional steps involved, z340 should have been solved long ago.
Do you have sample ciphers that are classically substituted but cannot be solved by AZDecrypt? I would almost certainly rule out a "straight homophonic substitution" variant like the one in z408.
Translated with http://www.DeepL.com/Translator
IMO, Z had definitely used a reference table for his letter frequencies. For certain letters he had used more homophones although the letter acutually occurs less often in his cleartext.
B vs. D (B occurs more often but has only one instead of two homophones)
F vs. G (G occurs more often but has only one instead of two homophones)
H vs. M (H and M occur equally often but a different amount of homophones was chosen)
L vs. A (A has four homophones instead of three, although the letter L actually occurs more often in his cleartext)
Thus, he must have had some type of frequency table looking like
Homophones / Letters
7: E
4: TAOINS
3: LR
2: DHF
1: BCGKMPUVWXY
while according to his cleartext a frequency table would actually look like this:
Homophones / Letters
7: E
5: TI
4: OL
3: ANSR
2: GHM
1: BCKPUVWXY
The differences are obvious. Also, according to the first table, the original letter frequency table Z had used must have had a frequency order like this:
E.TAOINS.LR.DHF.CUMPGWYBVKX
while a standard frequency table would usually look like this:
E.T.AO.INS.R.H.LD.CUM.FPGWYB.VKXJQZ
(e.g. ‘Scott Bryce’)
Something interesting: By using more homophones for the letter ‘L’, Z clearly had ‘preferred’ the letter ‘L’ over the letter ‘H’.
He also did so with the letter ‘F’ over the letter ‘C’. Nowadays, the opposite would be expected. To rank the letter ‘L’ more frequent than the letter ‘H’ is unusual. This might comply with his ceartext, but as we’ve seen previously, his frequency table did not derived from that one. It is possible, however, that Z had actually counted his own letters from different texts he had written. Those indeed might have had a more frequent ‘L’ than ‘H’.
In any case, Z had sort of a ‘weak’ reference table from either himself or some crappy cryptography book / magazine.
Well, besides that I still disagree (slightly) regarding the 340 not being a regular substitution cipher. However, I’ve been proven to be wrong regarding the possibility to solve such a complex cipher. In fact, we don’t know. What is interesting, however, is that in the 340 the bigrams/trigrams indeed occur mostly in the first part of the cipher, while they seem to be distributed quite equally in the 408.
Maybe we should start to think about what could cause such an irregularity? Why could bigrams occur less often towards the end of such a cipher?
QT
*ZODIACHRONOLOGY*
Thank you Quicktrader for the detailed description of the key frequencies! I will take a closer look at this, it looks really interesting.
Well, besides that I still disagree (slightly) regarding the 340 not being a regular substitution cipher. However, I’ve been proven to be wrong regarding the possibility to solve such a complex cipher. In fact, we don’t know. What is interesting, however, is that in the 340 the bigrams/trigrams indeed occur mostly in the first part of the cipher, while they seem to be distributed quite equally in the 408.
Maybe we should start to think about what could cause such an irregularity? Why could bigrams occur less often towards the end of such a cipher?
A few months ago I published a tool that allows you to create ciphers from ebooks. These can be filtered according to certain criteria. For example, Bigram discrepancies between the upper and lower half.
viewtopic.php?f=81&t=3709&p=58464
For testing I just took "Pride and Prejudice" from Project Gutenberg. Here one of the results as an example:
Ciphertext:
8q8rSsc0!OTFQUP7A jtkWxmhbKyc7tzmVO 8K8d!g51B2nGH!P6J CXYID""!Du!O43eFo C0DL1P!O6Sxpbl2Pv OPLTqu4ZCMwr7sU!O uutVPuJcSTAdvoBN3 xCW8e!!O58BHIMt7m Uwn2by6XfcNjd3dGH eKkCbJY5VoClOLP0F LO88zPDZ3OJcAM0dA N!P68xpL!O4Sue1zq UAWjrblBXxeIGMP2g sbfGt3OFmrQ!P5cNj YOC8dUK!P6Dxe7skP Lo8B0y!O4uVOJ1zDX 7pS!lb!D2PIj!O5AM 3xqHBgTcU!!P6FLO8 0yd1CWzP4IkMr7sTX QteF2O!P5bvcDNdKl
Plaintext:
WEWEREATYORKPROVI DEDSHECANHAVEHERO WNWAYBUTITELLYOUM ISSLIZZYIFYOUTAKE ITINTOYOURHEADTOG OONREFUSINGEVERYO FFEROFMARRIAGEINT HISWAYYOUWILLNEVE RGETAHUSBANDATALL ANDIAMSUREIDONOTK NOWWHOISTOMAINTAI NYOUWHENYOURFATHE RISDEADISHALLNOTB EABLETOKEEPYOUAND SOIWARNYOUIHAVEDO NEWITHYOUFROMTHIS VERYDAYITOLDYOUIN THELIBRARYYOUKNOW THATISHOULDNEVERS PEAKTOYOUAGAINAND
Bigrams upper half: 6
Trigrams lower: 0
Bigrams upper half: 20
Trigrams lower half: 5
Another example:
Ciphertext:
jxb7ncSodWOKefGpb LX8rT0PvA7scKk1zb 2BYxP4HlftZOTmcZP LdfIndW3ObjJC0D3g 50A8PMkoUyO8GPNw! O48O5Ilzc7pvPKqOL Bu!P6xdkfrrNGqu12 O!P6VXrHuD8ONlsU8 ytK!P58O6Ijzd7pYQ PFqMAuBxckMO3cZFr l!P4J!VsWPG50CONP u1zdKFDKw!O6uPS!O 4TFALjMqXZ3PH!kBe zblhmU0cANI!vVnd1 ouupi23OPJ5hxCeJc uSeBjuPV8yb1gqiPJ tWPu2xmJPScICuO6T hPJuOU3XQVDKvWuSP JdfSneixOuQTPJAXp uOUBP4vx0LO12Oyb7
Plaintext:
DHAVEAREASONABLEA NSWERTOGIVEANDTHA TISHOULDBESOREASO NABLEASTOADMITITB UTIWONDERHOWLONGY OUWOULDHAVEGONEON IFYOUHADBEENLEFTT OYOURSELFIWONDERW HENYOUWOULDHAVESP OKENIFIHADNOTASKE DYOUMYRESOLUTIONO FTHANKINGYOUFORYO URKINDNESSTOLYDIA HADCERTAINLYGREAT EFFECTTOOMUCHIAMA FRAIDFORWHATBECOM ESOFTHEMORALIFOUR COMFORTSPRINGSFRO MABREACHOFPROMISE FORIOUGHTNOTTOHAV
Bigrams upper half: 8
Trigrams lower: 1
Bigrams upper half: 17
Trigrams lower half: 1
In my opinion, the simplest explanation for such nGram discrepancies is the underlying plaintext. This can also be seen in the examples just shown. We prefer to search for symmetries and are amazed when they are broken. NGrams are not by nature evenly distributed over a cipher. Poetry, poems and song-texts have a certain tendency to generate such statistics. Zodiac also liked to repeat himself and his texts often had repetitive sections.
Of course, this does not automatically exclude another explanation. Nevertheless, here again I do not believe that z340 is behaving strangely in this respect. Rather, I will first stick to the simplest explanation.
Translated with http://www.DeepL.com/Translator
NGrams are not by nature evenly distributed over a cipher. Poetry, poems and song-texts have a certain tendency to generate such statistics.
Correct..not to forget the accidential use of homophones (and bigrams finding together, like drawing balls of different color from a bowl and accidentially getting three yellow ones in a row..).
This is actually why I still stick on the ‘standard’ homophone substitution. To be true, it seems to not even be easy to crack the Dorabella cipher, which most likely is actually no more than a regular substitution..promising results but, so far, nothing else. The 340 won’t be easier..this is why I don’t see need to do transposition etc., but there are different approaches, which is good. The winner takes it all. I hereby offer a total of $100 for the correct solution ![]() . Hey Zodiac, wanna earn some bucks?
. Hey Zodiac, wanna earn some bucks?
QT
*ZODIACHRONOLOGY*