More specifically, our simulations do completely agree on the macro scale.

That’s a great start. It means we essentially agree on the data set and the simulation algorithms.

In my previous posts, I’ve detailed, along with graphics of my simulation, how I used confidence intervals computed from the simulation’s set of results to compute the odds of these micro-level similarities to the keyboard. Was my argument unclear in any way? Or do you disagree with my statistical analysis?

One thing I would like to note is that a confidence interval of 95% does not mean the same thing as considering 95% of values in a normal distribution around the mean within 2 standard deviations. Based on your explanations in this thread, I understand that you mean the latter.

To answer your questions, I think your argument is clear but I respectfully disagree with parts of the analysis and its graphical representation.

I’ll start with an observation on how you plotted, in your latest graph, the "Actual distance in the 408 cipher" green data points and lines. This is the measurement that you use to determine if certain plaintext z408 symbol associations fall outside the 95%. Can you show how you calculated these points? I have some doubts on their accuracy. I redid a simulation but this time I executed it for a few plaintext letters individually to determine how frequently a random key for a single plaintext letter will be closer on a keyboard than the z408 key. I tested the letters E, N, O and T which are, according to your graph, outside or almost outside of the 95%.

E: 30% of random keys (composed of 5 symbols) are closer than the z408 key.
N: 48% of random keys (composed of 3 symbols) are closer than the z408 key.
O: 89% of random keys (composed of 3 symbols) are closer than the z408 key.
T: 71% of random keys (composed of 3 symbols) are closer than the z408 key.

These results are vastly different than yours.

Can you double-check your calculations on how you plotted the green line and share its formula? Let’s start with that. Thanks.

How do you guys consider the distances?

For example,

From X to X is 0.
From X to Z,S,D,C is 1.
From X to A,W,E,R,F,V is 2.

Correct?

Edit: thanks glurk.

How do you guys consider the distances?
For example,
From X to X is 0.
From X to Z,S,D,C is 1.
From X to A,W,E,R,F,V is 2.
Correct?

Exactly. That’s how I calculate it.

_pi, your simulation’s results sounds reasonable. Like you, though I forgot to explicitly clarify, I left out all Greek characters (except for the symbol used to represent P, which I thought was clearly pi, and from your former statements, I see might’ve been an incorrect presumption on my part) and / and + for the exact reasons you mention.

I’d like to respectfully disagree with your conclusion, however, on the basis of your metric. I almost used the same metric as you when I first set out to perform the simulation, but realized that the sum of all distances may be too reductive, and in effect, lose information about the micro-statistical distributions for each key.

More specifically, our simulations do completely agree on the macro scale. On average, a key is only about 5 spaces from any other key. For 20 plaintext symbols each represented by 2 characters on average, that’d suggest an overall average around 200 for the total distance metric (just a very rough estimate in my head without looking at exact numbers), which makes your 124 number sound very reasonable for the 12% point.

We differ in how we investigate the micro features of the key distribution. Specifically, my results show that he didn’t select certain keys very much below the expected distance; these keys were likely chosen by chance. But my results show that for a subset of the plaintext letters (6-8 of the 22 or 25-33%), the key does seem to mirror the keyboard more than statistically likely. Or without reference to statistical distributions at all, much like AK Wilks observed, 12-14 symbols are immediately adjacent "slam dunks."

In my previous posts, I’ve detailed, along with graphics of my simulation, how I used confidence intervals computed from the simulation’s set of results to compute the odds of these micro-level similarities to the keyboard. Was my argument unclear in any way? Or do you disagree with my statistical analysis? I don’t ask these questions rhetorically or heatedly, but truly in the interest of discussion of our methods; if I’ve made a logical error or statistical flub anywhere, I’d be happiest to know of the mistake to improve my skills as an objective scientist.

In essence, I think your methods are generally sound, but in effect, neglect the data’s variance, instead focusing only on its mean.

Perhaps we can both code a "slam-dunk test," because I think that test would simply and easily (without complicated statistics that might obfuscate my argument) capture this idea of variance at the micro-statistical level. I haven’t yet done so, so I’m not sure what the results will show. But perhaps it’s a good compromise before we completely dismiss the statistical significance of the observation.

I also would like to see the numbers resolved for the overall distance. But IMO even if the overall correct numbers come out closer to what Finder posted, as opposed to what Pi posted, it is not as convincing or potentially important as looking at the direct matches. As someone who has had both, based on different types of evidence I developed and presented, fairly successful and fairly unsuccessful interactions with the FBI, FBI Code Unit, a State Police Code Unit, the OCDA, SFPD and others, I don’t think the overall distance probability would be as convincing to them as the direct matches. It is still an important number to correctly determine. But when you are talking about Z average distances of two to three spaces away vs. longer for random, while that may be a strong enough result to assist further amateur and academic code researchers, it lacks the certainty and directness needed by law enforcement. or even most of the press. media, general public and general Zodiac research community.

Following up on the suggestions above by Finder, I think an observed Z408/QWERTY slam dunk vs. random test would be great. I think the number of slam dunk direct matches, immediately adjacent plaintext and ciphertext, SEEMS to be higher than what we would expect at random. if there is a way to test this, I think that may be the key.

I had said 12 to 14 instances, but after showing the C-E and the H-M to two people, not knowing anything else, both said C-E was NOT adjacent and both said that H-M was adjacent. So I find 13 instances of slam dunks.

What I will note here, after a very quick and rough look, is what I will call the "Slam Dunks". These are the plaintext and ciphertext that are IMMEDIATELY ADJACENT to each other. I am being conservative in judging what is "immediately adjacent.

Here are the Slam Dunks:

1. . A-S
2. . B-V
3. . D-F
4. . E-W
5. . G-R
7. H-M
7. . I-U
8. . I-K
9. . R-T
10. . T-H
11. U-Y
12. V-C
13. W-A

So by a quick and rough count we have at least 13 instances where the letters are right next to each other. I am open to discussion and debate if anyone things I am being too generous or too stingy. So if anyone finds distances of two spaces and up too attenuated and imprecise as a basis and with added statistical complexity, another study could be done to see how often it would randomly occur that 13 plaintexts are right next to their matching ciphertexts on a keyboard. It seems to me that 13 is rather extraordinary, and my spidey sense is tingling that this is NOT a coincidence, but right now nobody can say for sure. Maybe Finder, Pi and/or Doranchak can do a study on "Slam Dunks", i.e., immediately adjacent plaintext and ciphertext letters, that eventually would produce a hard number probability.

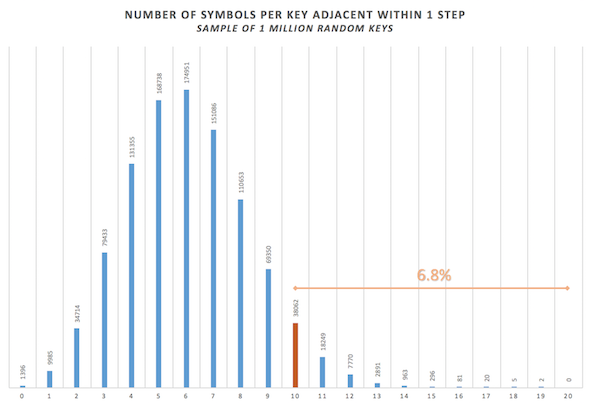
6.8% of random keys will exhibit an equal or higher number of symbols adjacent within 1 step of their plaintext letter compared to the z408 key:

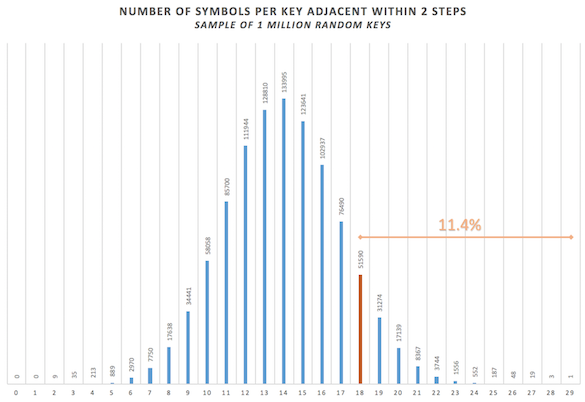
11.4% of random keys will exhibit an equal or higher number of symbols adjacent within 2 steps of their plaintext letter compared to the z408 key:

So, by only considering 1-step or 2-step adjacency, the z408 key is clearly closer to its plaintext than the average random key without however being exceptional.

The reason I initially analyzed the average distances of all the symbols on the keyboard was to evaluate the validity of a general idea: that the zodiac picked his letter-like symbols around the plaintext letters on a qwerty keyboard. Now, if you are to only consider the symbols that comfort this hypothesis (and exclude symbols that hinder the hypothesis), you are essentially saying that the zodiac’s strategy was the following:

– from the pool of 54 symbols, pick 10 to 18 that are close to the plaintext letters on a keyboard.
– then, pick another 21 to 29 letter symbols at random or using a different method.
– then, use random pictograms for the rest.

This means that an attempt at deducing the encoding strategy of the z408 is derived by only considering 19% to 33% of the z408 key construction. And even then, the portion of the key chosen to make this deduction, while exhibiting properties outside of the norm, does not show, in my opinion, exceptional traits. I think this is far from sufficient to demonstrate a pattern of thought.

_pi

Chart of One Step Study by pi Showing Z408 One Steps of 10 or More For 6.8% of Randoms

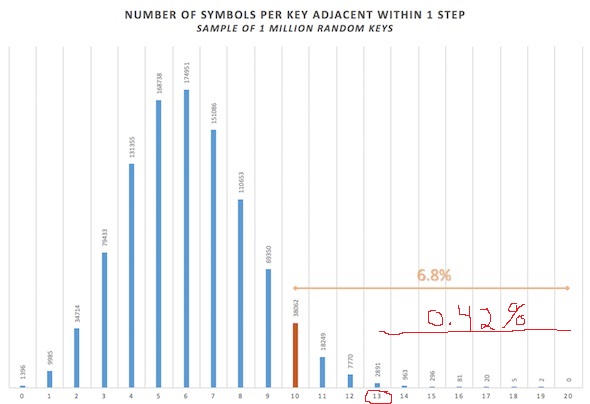
Chart of One Step Study by pi Modified BY AK Wilks to Show Actual Observed Z408 One Steps of 13 or More For 0.42% of Randoms

Thanks for doing this work. It is only through fair skepticism and impartial study that we can test observations. I never counted the number of two steps in the Z408 so I cannot comment on that study. My thought is that the most important thing to look at is the one steps, those immediately adjacent.

Question: You seem to start at 10 or more adjacent matches, which happened just over 68, 000 times, to get your 6.8% number? So randomly about 1 out of 15 times?

I observed the Z408 to have 13 instances of adjacent plaintext/ciphertext. In the randoms 13 or more adjacents happened only 4,258 times, which would create a much lower percentage, like 0.42%? (Or 4/10 of 1%?) So randomly about 1 out of 250 times?

Are my numbers and math correct?

There are only 10 directly adjacent matches. The additional 3 you are counting are not directly adjacent but are measurably closer than 2 steps; they could be considered 1.5 steps away. We could redo the analysis by counting the actual physical distance between the center of each key… Currently, I count the distances in integers as in the following example:

From letter G, the letters H,Y,T,F,V,B are 1 step away. The letters R,D,C,N,J,U are 2 steps away.

Also, the 0.42% value is not correct. If you are considering keys that are, let’s say, 1.5 steps away, you would have to also allow 1.5 steps away during the generation of random keys.

So, rerunning the program while considering these 1.5 steps away, we get that 1.3% of random keys are similar or closer to the 13 letters in the z408 that are within 1.5 steps. So, considering the 1.5 distance makes the subset on average closer than considering only 1-step or 2-steps distances.

I asked for objections on my 13 and did not get any, so I assumed we all agreed on the 13.

There are no letters between G & R. They are adjacent diagonally. They are a one step.

What 3 of mine are you saying are not adjacent?

So by a quick and rough count we have at least 13 instances where the letters are right next to each other. I am open to discussion and debate if anyone things I am being too generous or too stingy.

5. G-R
7. H-M
10. T-H

They are not touching each other. I agree they are closer than 2-steps away but I disagree they should be considered as close as "B-V" for example.

"H-M" is the worst one of the 3 since, as you will notice, the way the top 2 rows on a keyboard make top-left-bottom-right distances smaller than the bottom 2 rows.

Anyway, that’s why I mention in my last post that at this point, if we are starting to compare half-distances, a more precise evaluation would be to measure the actual distance between keys instead.

Well I strongly disagree on G-R and T-H. I don’t think Z was sitting there with a ruler on his typewriter to determine his code. My criteria is how an average human eye would see something as adjacent. For most letters on the middle line of the keyboard there are typically 9 adjacent letters – 2 vertical (1 above, 1 below), 2 horizontal (1 left, 1 right) and 4 diagonal (1 NE, 1 SE, 1 SW, 1 NW). I think the G-R and the T-H are clearly adjacent as the human eye and mind view them. The H-M is more debatable, which is why I initially excluded it and the C-E. But doranchak noted it as adjacent in an earlier post, and I asked two people for opinions on it and both said H-M was adjacent, the H being NE to the M. So I put H-M in, and nobody objected.

Perhaps you could do calculations, one with 13 as adjacents and one with 12 (excluding the H-M).

For the 13 I get 4,258 times out of 1,000,000, which gives us the 0.42% number. For the 12 it becomes 12,028 out of 1,000,000, so about 1.2%.

So if I am correct in the 13 it would happen by chance 1 out of 250 times, which I would say most would think is statistically significant. For 13 plaintexts to match 13 ciphertexts only happening by chance 1 out of 250 times, I find very significant when we observe that Z did this with the 408, and IMO that shows a good working hypothesis that it was probably intentional, and certainly worth examining the 340 using a QWERTY analysis to see if it might help us solve any symbols and/or give us some insights into Z’s background and thought process. Could he have used something similar to create part of the 340? QWERTY Keyboard? The periodic table? Greek letters? Letters for numbers? Something else simple and right in front of our eyes, hiding in plain sight, like a typewriter keyboard?

If we go with 12 it would happen about 1 out of 84 times, which I would say most might find right on the borderline of being statistically significant, and leaning towards it. For 12 plaintexts to be adjacent to 12 ciphertexts only happening 1 out of 84 times by chance, and yet we observe that is what Z did in the 408, I personally would find that interesting enough to warrant further study and to look at the 340 with the idea to see if a QWERTY analysis can help us solve any symbols.

Perhaps you could do calculations, one with 13 as adjacents and one with 12 (excluding the H-M).

That would probably be the best approach to remove our disagreeing definitions of adjacency from the equation.

For the 13 I get the 0.42% number.

My latest graph still stands. Let’s not call them 1.5 steps but distances of 1 where we include diagonals such as "G-R". What you have to understand is that I had to regenerate 1 million new random keys where these new keys would also consider diagonals such as "G-R" as distances of 1 whereas before, they were considered as distances of 2. That’s why there are more keys that now fit this criteria.

So, 1.3% of random keys are similar or closer to the 13 letters in the z408.

Well in your original calculation you ARE including diagonals. For the G you are including the Y, B and V as diagonals. IMO there is no reason to differentiate the R and exclude it.

But yes since we disagree the best path may be to do two calculations, one with 13 and one with 12.

As a side issue, what do others think? 10 or 13? Go strictly by distance, which may be more precise but loses the human element? Or go by how Z likely did it (if he did it), the human eye and mind perception of what is adjacent? Which is less precise but IMO more likely how a person would actually use a keyboard to help create a code?

Anyway, even with others chiming in, unless there is a clear consensus one way or the other, it may be best to do both the 12 and the 13.

For others, imagine if a person decided to use a typewriter keyboard to help create a code, and decided to link plaintext to ciphertext by using keys that surround another key, in other words use keys that are adjacent or neighbors. Which letters meet that criteria? Are these keys adjacent?

1. G-R
2. H-M
3. T-H

I was including diagonals that I considered to be 1-step, such as R-F, G-Y. Not diagonals that I was not considering as 1-step diagonals such as R-G.

That’s why I initially only considered 10 adjacent letters and generated random keys that would not consider R-G type of diagonals.

After some exchanges with you, I then considered 13 adjacent letters and generated random keys that would consider R-G type of diagonals. This has the effect of relaxing the adjacency constraint and thus, increasing the number of random keys that exhibit more closeness than the z408.

I then generated the latest graph, and found the new 1.3% metric.

OK I see your point and where you get the 1.3%. But the G-R & T-H are one steps, should have been included as such, you did include diagonals like G-Y, and thus IMO the 0.4% is valid. Maybe Finder or Doranchak can do a study to back up yours.

But let us assume you are right. For me personally, for something to happen by chance only 1.3% of the time, so by chance 1 out of 77 times and we see that result in the Z408, IMO it merits further study and a working hypothesis that Z may have used a keyboard to create part of the 408, and thus it is worth my time to look at the 340 with that idea in mind. But the 1.3% number may be borderline for some people, and some may not consider it significant enough, but I think most will. I think the 0.4% number, by chance 1 out of 250 times, almost everyone would consider that to be definitely significant.

I think based on the varying results, it’s fair to suspect that the cipher author may have used a keyboard layout in some way to assist in making the symbol/letter assignments. But I can’t bring myself to say that a 1 out of 250 probability would be a statistical slam dunk, especially considering the variance of probability based on the initial assumptions during the randomized trials.

Also, the randomized trials assume we are only interested in finding keys that show adjacencies to typewriter key layouts. But they do not look for other adjacencies that, if present, would have generated interest among researchers (such as the periodic table, to use AK’s example). So, "odds of a random key lining up to the QWERTY layout" becomes "odds of a random key lining up to any interesting layout", a much broader criteria that would obviously increase the chances.

Still, it is a very interesting phenomenon, which reminds me of the "prime phobia" aspect of the 340. Because the "+" symbols occur a lot in the cipher, you’d expect them to fall on several of the 68 prime-numbered "slots" of the 340 cipher. But only one does. In random trials, 2.9% of shuffled ciphers with the same distribution of symbols have the same "prime-phobic" quality of the "+" symbol. Things get a little more interesting when you consider the "B" symbol, the 2nd most frequent symbol in the cipher, which is also prime-phobic: it, too, falls on only one prime-numbered spot. If you include that observation in randomized trials, you find that 1 in 143 shuffled ciphers have the same prime-phobia in its top two frequent symbols.

Rare enough to generate interest, but not so rare that it’s completely undeniable!