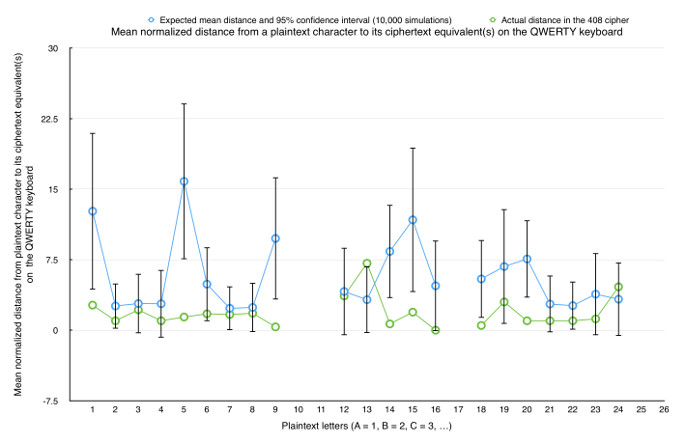
In response to doranchak’s suggestion, I programmed a simple simulation.
Each run of the simulation randomly generates a key with a similar distribution to that of the 408 (i.e. ‘A’ must be represented by 3 other letters on the keyboard, ‘B’ must be represented by 1, ‘C’ must be represented by 1, ‘D’ must be represented by 1, ‘E” must be represented by 5, etc. Refer to the graphic in Jarlve’s post if you’re not clear on what I mean.).
Then, each run computes the average distance (on the QWERTY keyboard) from the plaintext character to its ciphertext equivalents. For example, in the 408, the V in the ciphertext represents B in the plaintext, so B is, on average, 1 unit of distance away from its ciphertext equivalent, V.
At the conclusion of N simulations, the program then computes the mean distance and its variance between each plaintext character and its ciphertext equivalent(s).
Here are the initial results for N = 10,000. I think the plot’s sufficiently descriptive of its content to omit further description here.
My interpretation: The plot shows that 8 of the 22 plaintext letters (A, E, I, N, O, P, R, and T) are closer than the simulation’s 95% confidence interval would predict. Should we consider that significant? I think so, but I’d like to hear from you.
In the interest of full disclosure, I wrote the program rather quickly, so it’s possible I’ve made an error somewhere. I’ll review the code further, and I plan to rewrite the program in another language when I’ve got a chance. But as of now, these initial results seem reasonable. If anyone wants me to upload the code, I’d be happy to upload the second (cleaner) draft at a later time.
I’d like to hear your thoughts.
(A, E, I, N, O, P, R, and T)
Maybe we could consider that A POINTER ![]()
(I N A P P R O P R I A T E) ![]()
Bumping for possible interest due to a similarity to Marie’s code roads or paths theory. Ignore my writing and go to the bottom to see the code paths or playing tag. Though in general, I think this observation by finder and analysis by pi, doranchak and others, made a good showing that Z probably used a typewriter to create a large part of the 408 code. Thus meaning perhaps he used a typewriter and/or some other fixed reference point (like the periodic table) to help make a large part of the 340 code.
I think based on the varying results, it’s fair to suspect that the cipher author may have used a keyboard layout in some way to assist in making the symbol/letter assignments. But I can’t bring myself to say that a 1 out of 250 probability would be a statistical slam dunk, especially considering the variance of probability based on the initial assumptions during the randomized trials.
Also, the randomized trials assume we are only interested in finding keys that show adjacencies to typewriter key layouts. But they do not look for other adjacencies that, if present, would have generated interest among researchers (such as the periodic table, to use AK’s example). So, "odds of a random key lining up to the QWERTY layout" becomes "odds of a random key lining up to any interesting layout", a much broader criteria that would obviously increase the chances.
Still, it is a very interesting phenomenon, which reminds me of the "prime phobia" aspect of the 340. Because the "+" symbols occur a lot in the cipher, you’d expect them to fall on several of the 68 prime-numbered "slots" of the 340 cipher. But only one does. In random trials, 2.9% of shuffled ciphers with the same distribution of symbols have the same "prime-phobic" quality of the "+" symbol. Things get a little more interesting when you consider the "B" symbol, the 2nd most frequent symbol in the cipher, which is also prime-phobic: it, too, falls on only one prime-numbered spot. If you include that observation in randomized trials, you find that 1 in 143 shuffled ciphers have the same prime-phobia in its top two frequent symbols.
Rare enough to generate interest, but not so rare that it completely undeniable!
I think Doranchak states the situation pretty well. If we use pi’s analysis, we come out with 1.3% of randoms having equal or greater number of matches, which is about 1 out of 77 odds of the observed Z408 happening by chance. Using my analysis it is 0.4%, which is 1 out of 250. Doranchak states "I think based on the varying results, it’s fair to suspect that the cipher author may have used a keyboard layout in some way to assist in making the symbol/letter assignments." I agree, and would go even further, from suspecting the cipher author may have used a keyboard to suspecting he probably did.
I think Doranchak accurately states how some code and math people look at odds like these, or the prime phobic Z odds of 2.9% [1 out of 34] for the most frequent symbol (+) or 0.69 % [1 out of 143] if we include the second most frequent symbol (B).And the frustrating things is if Zodiac was as smart as I think he was, he may have had a rough idea about some of these types of things. He didn’t tend to do things that were obvious giveaways. He avoided black and white, instead he usually kept it in the grey zone. If he was prime phobic, he did it enough to raise eyebrows but not enough to absolutely convince. If he used a typewriter keyboard, he only did it for part of his key. Again, enough to leave a tantalizing clue, but not enough times to prove he absolutely for sure did it.
I look at things a little different. We are all partially a product of our education, experience and background. My experience includes being a military policeman in the Army and a criminal defense lawyer. If in the real world I see something happen, and find out there is a 1% chance it happened randomly, I view that as a 99% chance it was not random. For example, if someone took two card decks so there were 100 cards in them and only one joker, and I go to a crime scene and see a joker card, and find that 100 card deck in the suspects house with no joker present, I look at that as a strong suspicion that the joker from that deck was placed there. Yes it is a 1% chance, but in the real world, it looks damn suspicious.
Scott Peterson never went fishing, except for the day his wife went missing. So if Scott says that was just a coincidence do you believe him? Or like a scene from the movie "The Counselor". A man is explaining that it was just a "coincidence" that a man he got out of jail was later set up and robbed of a drug shipment. The representative of the drug cartels explains "The people I work for are very practical. They don’t believe in coincidences. They’ve heard of them, they’ve just never seen one." One more movie scene analogy, from "Casino". Two slot machines get hit for huge money payoffs back to back. The casino manager asks the slot chief "Didn’t you know it was a scam, didn’t you know you were being set up?" The slot chief says "There is no way to tell that for sure." The manager says "Yes there is, there’s an infallible way. They won."
I guess that is my longwinded way of saying that yes for a mathematician a 1.3% or even 0.4% chance of something happening may not be a statistical slam dunk. But in the real world of criminals we seldom see things with those odds happen by chance. So when I see odds that something happens by chance 1.3% of the time, 1 out of 77 times (pi’s calculation) and that is what we see, I find it suspicious and worthy of further study. When I see something that happens by chance only 0.4% of the time by chance, 1 out of 250 times (my calculation), and that is what we see Zodiac did, I find it highly suspect and well deserving of much further study.
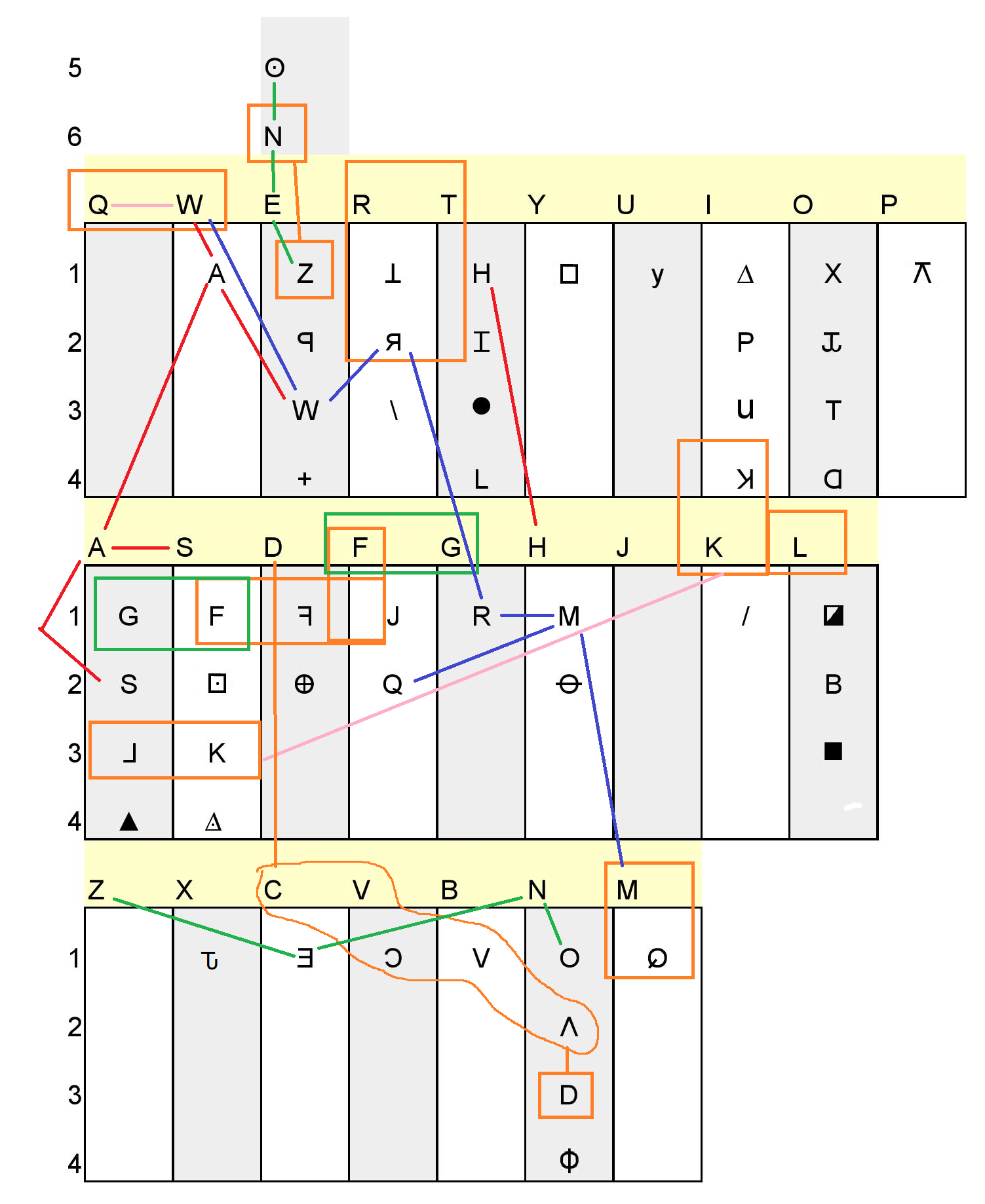
Anyway, here is a typewriter keyboard marked only with what I consider to be the slam dunk adjacent matches of plaintext-ciphertext.
They show the observed adjacent matches in the Zodiac 408 key which are:
1. . A-S
2. . B-V
3. . D-F
4. . E-W
5. . G-R
7. H-M
7. . I-U
8. . I-K
9. . R-T
10. . T-H
11. U-Y
12. V-C
13. W-A1. I just noticed something. He seems to have started with a pretty good run with A, B, D, E, G, H. And then picks it up later to finish with another good run with R, T, U, V, W. What seems to be excluded is everything from J to Q. Which in Z408 terms means K, L, M, N, O, P are excluded, the middle range of the alphabet. Did he use something else? Was this intentional so as not giveaway to clearly that he used a keyboard for part? To keep the results in that grey range Doranchak talks about, enough to be suspicious and be a teasing clue, but not enough to be a clear result. Or just chance? Or does it mean something else? It appears he did it for the first 6 letters and the last 5 letters, but excludes the 6 in the middle. If Zodiac did NOT use the typewriter keyboard intentionally, and this is all just random, it just got weirder. How many random trials would show the first six and last five matching to a keyboard, but the middle six with no matches at all? if this is all just truly random and not intentional, shouldn’t the matches and non matches be spread out?
2. I just noticed something else! Some of the matched letters appear to "play tag" with each other. What percentage of randoms would show a similar pattern? So B=V, then V=C. In fact:
B – V – C
E – W – A – S
G – R – T – H – M
I – U – Y
MODERATOR
For people who find this keyboard theory to be outside the realm of believably, please watch this video:
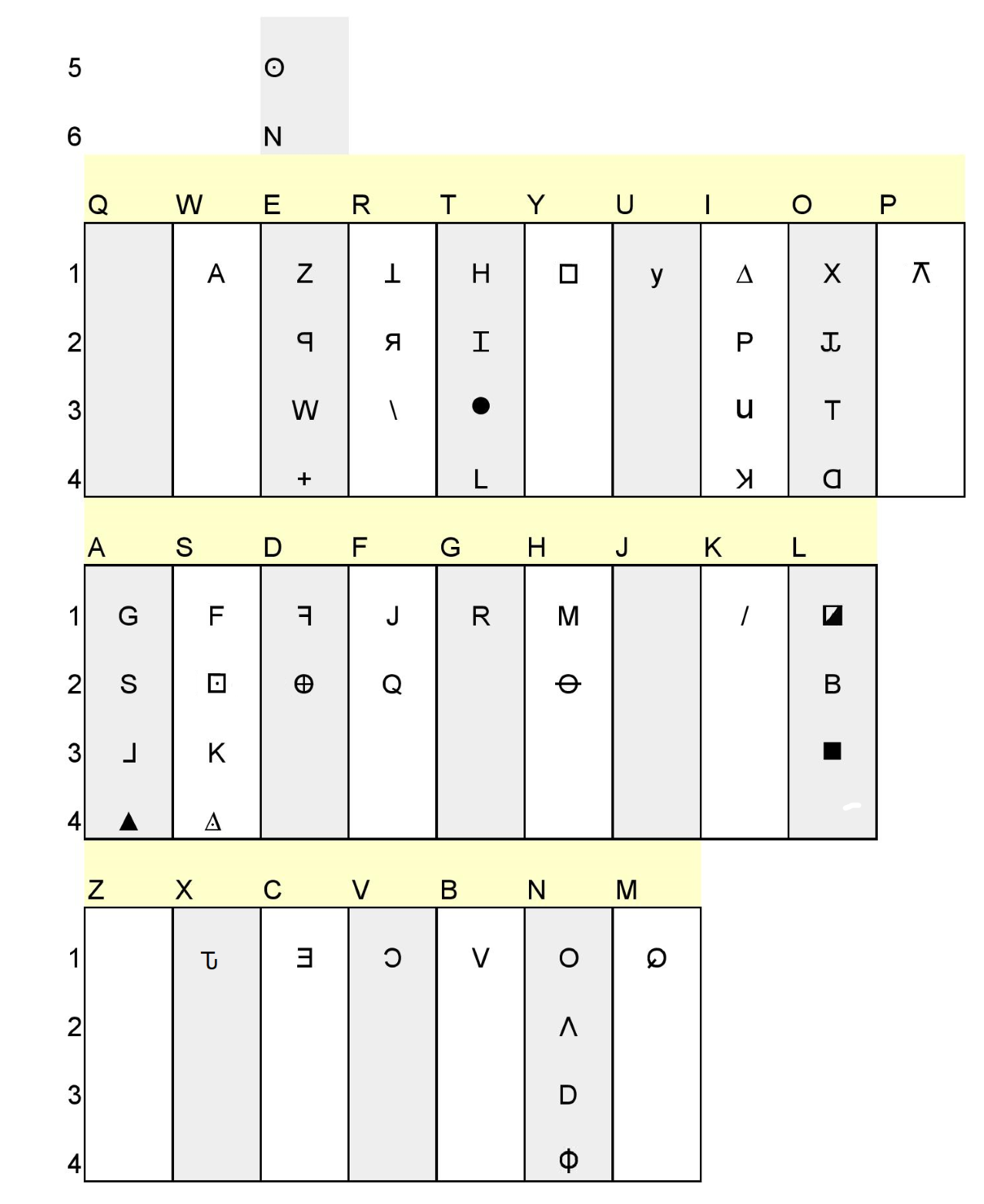
If anyone is interested, I drew up a new key for the 408 that Includes what I think are the correct cycle positions for each symbol and which is organized by a standard keyboard layout.
There is another key that has been floating around but I think it has the incorrect orientation for L1.
If anyone is interested, I drew up a new key for the 408 that Includes what I think are the correct cycle positions for each symbol and which is organized by a standard keyboard layout.
Thanks, very handy!
I’m telling you, there’s something going on here. This cannot be my imagination.
There is something systemic about how he makes the symbol assignments. I don’t think this was a table with substitutions. Maybe it was more like some kind of matrix
Has anyone ever seen something that looks like this?
I don’t know what to make of this, but, without reading too much into it, it’s just weird.
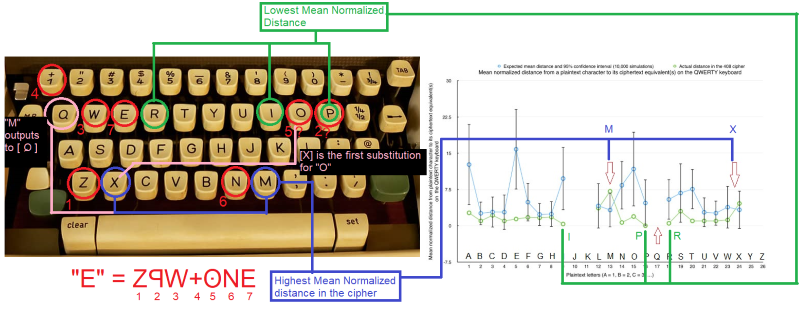
If we give some leeway for reflections and dots in the symbol assignments, it seems like "E" ends up substituting to the four corners of the keyboard and snuggling up to the weirdo letters [M, Q, X, O]
Also, the first substitution for "N" is [O], which is weird since [dotO-N-E] concludes the substitution sequence for "E."
I don’t know exactly where I’m going with this. It could be the result of sampling too many letters and their substitutions, or over-analyzing similarities in the symbols. I just find it so utterly bizarre that the statistical outliers in Finder’s graph seem so bunched up in the four corners, particularly since "E" also seems to be doing that. Particularly odd since "everything comes back to ‘E’." Did I mention I find this weird?
EDIT: Also, I know this graph was updated later but the statistical outliers were still the same. This seems like a really hard connection to map statistically, too. As has been pointed out, special characters didn’t have a consistent location on old school QWERTY keyboards. There’s a ton of ambiguity when you throw reflected or rotated symbols into the mix because so many letters are vertically and/or horizontally symmetrical. What does a backwards [X] look like, anyways?
There might be one more thing to consider here.
I didn’t realize that the history of keyboard layouts was such a controversial subject mired in folklore, but the impression I get is that QWERTY and the like are optimized for bigrams in English (and similar Latin Script). In other words, QWERTY is full of n-grams, and I’m just wondering if this is such a straightforward observation because I imagine you could get similar distributions by taking all the vowels in English and putting them on either side of all the consonants in English, measure the mean distance and get a similar deviation from randomly generated keys. That’s basically what QWERTY is after all.
That’s not to say that an actual keyboard layout is unrelated to the construction of the 408 key, but maybe there’s a risk of confirmation bias here (If you’ve read my posts, you probably know I am consistently guilty of this exact thing)
Particularly odd since "everything comes back to ‘E’." Did I mention I find this weird?
This is marie’s or margie’s observation right? I’ve been wanting to look into this sometime.
That’s not to say that an actual keyboard layout is unrelated to the construction of the 408 key, but maybe there’s a risk of confirmation bias here.
I think it is simple what to do here, we need to statistically test if the keyboard observation has any significance.
I think it is simple what to do here, we need to statistically test if the keyboard observation has any significance.
My memory is failing me, it seems this was already done by _pi:
Here are the corrected values by keyboard layout. The error I initially made in the post I deleted was to compare, for example, a random key applied to the azerty layout with the z408 key applied to the qwerty layout, as opposed to comparing it to the z408 key applied to the azerty layout.
I generated 10 million random keys to compare them to the z408 key on how many directly adjacent letter symbols can be found, per keyboard layout.
qwerty: 1.3% of random keys exhibit an equal or higher adjacency than the z408 key (as seen in previous posts)
azerty: 6.48% of random keys exhibit an equal or higher adjacency than the z408 key
qwertz: 7.37% of random keys exhibit an equal or higher adjacency than the z408 key
Dvorak: 14.25% of random keys exhibit an equal or higher adjacency than the z408 keyThe z408 key exhibits a higher affinity with the qwerty keyboard than with the others, in terms of number of symbol letters being directly adjacent to their plaintext letter.
And also this:
In response to doranchak’s suggestion, I programmed a simple simulation.
Each run of the simulation randomly generates a key with a similar distribution to that of the 408 (i.e. ‘A’ must be represented by 3 other letters on the keyboard, ‘B’ must be represented by 1, ‘C’ must be represented by 1, ‘D’ must be represented by 1, ‘E” must be represented by 5, etc. Refer to the graphic in Jarlve’s post if you’re not clear on what I mean.).
Then, each run computes the average distance (on the QWERTY keyboard) from the plaintext character to its ciphertext equivalents. For example, in the 408, the V in the ciphertext represents B in the plaintext, so B is, on average, 1 unit of distance away from its ciphertext equivalent, V.
At the conclusion of N simulations, the program then computes the mean distance and its variance between each plaintext character and its ciphertext equivalent(s).
Here are the initial results for N = 10,000. I think the plot’s sufficiently descriptive of its content to omit further description here.
My interpretation: The plot shows that 8 of the 22 plaintext letters (A, E, I, N, O, P, R, and T) are closer than the simulation’s 95% confidence interval would predict. Should we consider that significant? I think so, but I’d like to hear from you.
In the interest of full disclosure, I wrote the program rather quickly, so it’s possible I’ve made an error somewhere. I’ll review the code further, and I plan to rewrite the program in another language when I’ve got a chance. But as of now, these initial results seem reasonable. If anyone wants me to upload the code, I’d be happy to upload the second (cleaner) draft at a later time.
I’d like to hear your thoughts.
Hi guys! It’s been a while since I’ve logged on! I was blown away by the news about the 340. Congratulations to all of you who’ve worked so hard on this! What an incredible, incredible achievement. I’m so happy for all of you.
I’ve just taken a look at the 340 key alongside the QWERTY keyboard, and we can immediately notice some parallels between the keyboard layout and the 340 key. Here are my observations:
Reversed L and O and K decode to A. L, O, and K are right next to each other on the keyboard.
S and A decode to D, which is next to S and A on the keyboard.
B and N, which are adjacent on the keyboard, decode to E.
Reversed K decodes to I, which is next to K on the keyboard. H and reversed Y decode to I, and H and Y are adjacent on the keyboard.
E and T decode to R, which is next to E and T on the keyboard.
U and J, which are adjacent on the keyboard, decode to S.
G decodes to T, which is next to T on the keyboard.
C and X, which are next to each other on the keyboard, decode to Y.
I’m not sure that these observations are statistically significant, but I was drawn to make the comparison once I’d heard the 340 had been cracked. Maybe I’ll write another program to test the likelihood of the observations.
Once more: congratulations, congratulations, congratulations!
see me next post.
see me next post. I try to insert image sorry I am new.