Yes it’s allot of fun, I’m also getting a bit tired into the week and won’t be able to come up with anything today but it is being worked on.

Edit: I did look a bit further into the even/uneven discrepancy and figured it out (I hope).

This is something new I came up with that measures the difference in counts between symbols on even/uneven/every n’th positions and so forth. I’m only going to post the relevant numbers but I did inspect all your ciphers. Interval 2 is even/uneven, etc.

Symbol measurements:

408:
Interval 2: 67 <– as expected (below 100)
Interval 3: 96
Interval 4: 99

340:
Interval 2: 124 <– a bit high
Interval 3: 125
Interval 4: 100

smokie1:
Interval 2: 152 <– very high
Interval 3: 109
Interval 4: 111

smokie7:
Interval 2: 138
Interval 3: 60 <– 3 parts interlaced cipher identified
Interval 4: 104

smokie8:
Interval 2: 169 <– very high
Interval 3: 105
Interval 4: 138

At first I didn’t understand why smokie1 and 8 were so high but then I checked out the smokie1 plaintext, which is the purple haze message.

smokie1 plaintext (from solver):
Interval 2: 255 <– what?
Interval 3: 52
Interval 4: 173

408 plaintext (340 characters):
Interval 2: 68
Interval 3: 97
Interval 4: 100

So it seems that I’m measuring the plaintext through the cipher. Comparing the top versus bottom halves:

smokie1:
Top half: 86
Bottom half: 184

smokie8:
Top half: 77
Bottom half: 169

smokie1 plaintext (from solver):
Top half: 65
Bottom half: 342

Very big discrepancy between top and bottom half.

It may be trivial for our current experiments but I believe you used the purple haze plaintext for the smokie8, if not, it’s one hell of a coincidence. So I’m pretty sure it’s a dead lead. I’m going back to the cycles for a more in-depth look (I won’t try to capitalize on knowing the plaintext).

I spent a few minutes making my cycle spreadsheet so that conditional formatting shows whether a symbol is odd or even. Then I looked at the top scoring cycles on the 340 to see if any of the 34 highest scoring cycles (score 256 or more) are exclusively odd – even – odd – even, etc., or exclusively odd or exclusively even.

There are nine symbols unique to the odds:

37, 38, 41, 43, 45, 49, 58, 59, and 61.

38 is an even numbered symbol, but first appears at position 41 and 58 is an even numbered symbol but first appears at position 109.

There are five symbols unique to the evens:

12, 48, 52, 60 and 62.

37 cycles with 41 in the top thirty four cycles, and 38 cycles with 41 in the top thirty four cycles. EDIT: There are 1953 total cycles. Twenty three cycles score in the 256 range. When I randomize the 340, I get an average of 6.1 such cycles. The 37 – 41 cycle has the familiar repetition of the last symbol toward the end.

37 41 37 41 37 41 37 41 37 37 37
38 41 38 41 38 41 38 41 38

It could just be a coincidence and those are the only patterns that I can find. There is no high scoring cycle that is odd – even – odd – even, etc. I am going to try to conditional format for 3 parts and 4 parts and look for patterns there too.

EDIT: I checked the top 34 two symbol cycles for cycled 3 keys, 4 keys and 5 keys. My findings are that there are no other high scoring cycles that are all in the same parts or cycle with the parts. In other words, there is no other cycle that occurs on only one part, or Part 1, then Part 2, then Part 3, then Part 1 again, etc.

I am going back to work on the table now.

Does anybody know how to calculate the probability of this happening:

37 41 37 41 37 41 37 41 37 37 37

And this happening:

38 41 38 41 38 41 38 41 38

Where all of the symbols land on odd numbered positions?

By the way, since both share 41, I checked the three symbol cycle:

37 38 41 37 38 41 37 38 41 38 37 41 37 38 37 37

Three repetitions of the three symbol cycle, and then random.

I’m not equipped to answer your question directly, but I can say what I’ve discovered in my own experiments.

In Z340, the cycle 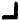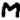is very strong. In fact, it repeats perfectly 7 times in a row, with no leftovers. No cycle of length 2 is better than that one.

So, I ran some shuffle tests to answer this question: How many random shuffles does it take (on average) to generate a sequence as good as or better than that one?

I ran 100 trials and found that on average, it takes 83 shuffles before a similarly strong sequence is produced.

The cycle pattern seems very strong in Z340 but it’s still not far from chance. So, generally speaking, it seems very possible that these sorts of patterns appear naturally. But, since there are other interesting cycle patterns in Z340, a more useful question might be: How often do random shuffles generate a set of interesting cycles that is as good as or better than the set of interesting cycles found in Z340? Looks like you’ve explored the answer to that question already if I’m not mistaken.

My general sense is this: The strong cycle patterns we see in Z340 can’t individually be separated from chance. But, the distribution of patterns in Z340 might be.

I have failed to address the "odd positions" part of your question, however. That adds an interesting complexity to it. Do you have a number to symbol lookup I can refer to? Unfortunately, my tools are all using symbols instead of numbers.

Yeah, sure. We are exploring the possibility that Zodiac may have used two keys and alternated the keys when encoding. Symbols 37, 38 and 41 are unique to odd numbered positions, which makes me think that he had those symbols on alleged Key 1 but not alleged Key 2.

Here is my conversion table, which I hope is correct:

Otherwise, here is the 37 – 38 – 41 cycle. All symbols fall on odd numbered positions. A=37, B=38, and C=41.

Note that there is three symbol cycling in the first half, but not in the second half. The two symbol cycling continues into Row 12. Most of the symbols appear in the first half.

Is this statistically significant when they all land on odd numbered positions?

EDIT: Is this statistically significant when only looking at the first 170 symbols versus all 340 and they land on odd numbered positions?

Thanks.

EDIT: Note to self: Check the first half and the second half to find out what symbols are mutually exclusive with respect to odds and evens in the two halves.

Jarlve, I got sidetracked tonight. And am studying something for work very extensively lately. Tell me if you want me to tell you if smokie8 is the purplehaze message or not. Otherwise, I will not tell you. At this point, I think that I need to have my own head examined.

I’ll chip in with the discussion later.

I just finished a bit of work on top scoring cycles, here are some results for the 340:

2 symbol cycle: lM lM lM lM lM lM lM By appearance: 6 37 6 37 6 37 6 37 6 37 6 37 6 37
3 symbol cycle: RKM RKM RKM RKRMKRM RKM RMK By appearance: 3 31 37 3 31 37 3 31 37 3 31 3 37 31 3 37 3 31 37 3 37 31
4 symbol cycle: |BOBcO| Oc|OBcOB|BOc|B|BccB|cBOcB|cO |BOBcO| By appearance: 11 20 23 20 36 23 11 23 36 11 23 20 36 23 20 11 20 23 36 11 20 11 20 36 36 20 11 36 20 23 36 20 11 36 23 11 20 23 20 36 23 11

I am filling the table. Jarlve, you post number pairs for your cycle scores (e.g. 4037/ 196). That is how I am filling the table. When you get back to the 340, I may need those pairs as I seem to only find the number on the right.

Here is the format. There are other messages to the right not yet shown, such as m5p1, smokie6, and smokie5.

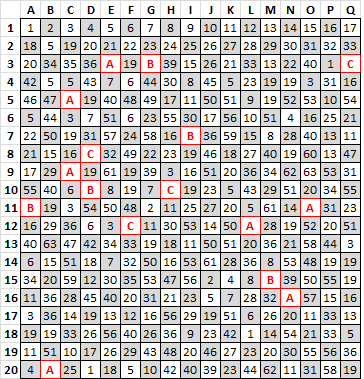
OK, I did a search for cycles that fall on even/odd positions.

Your example is this one:

[MUJ] [MUJ] [MUJ] UMJMUMM

It cycles three times, and all of the symbols (including the "leftovers") fall on odd-numbered positions.

I looked for similar cycles for L=2,3,4 for Z340, a shuffled Z340, and Z408. Here are the results:

Z340, L=2:

[UJ] [UJ] [UJ] [UJ] U (ALL ODD POSITIONS)
[MJ] [MJ] [MJ] [MJ] MMM (ALL ODD POSITIONS)
[7;] [7;] [7;] (ALL ODD POSITIONS)
J [Jb] [Jb] [Jb] (ALL ODD POSITIONS)
[MU] [MU] [MU] UM [MU] MM (ALL ODD POSITIONS)
[&A] [&A] (ALL EVEN POSITIONS)
[jX] [jX] (ALL ODD POSITIONS)
[73] [73] 7 (ALL ODD POSITIONS)
[7X] [7X] 7 (ALL ODD POSITIONS)
[;X] [;X] ; (ALL ODD POSITIONS)
[j;] [j;] ; (ALL ODD POSITIONS)
[t&] [t&] tt (ALL EVEN POSITIONS)
[Jj] [Jj] JJ (ALL ODD POSITIONS)
[7b] [7b] b7 (ALL ODD POSITIONS)
;b [b;] [b;] (ALL ODD POSITIONS)
[Uj] [Uj] UUU (ALL ODD POSITIONS)
[J7] J [J7] [J7] (ALL ODD POSITIONS)
[U;] UU [U;] [U;] (ALL ODD POSITIONS)

Z340, L=3:

[MUJ] [MUJ] [MUJ] UMJMUMM (ALL ODD POSITIONS)
[j;X] [j;X] ; (ALL ODD POSITIONS)
[7;X] [7;X] 7; (ALL ODD POSITIONS)
[UJj] [UJj] UJUJU (ALL ODD POSITIONS)

Z340, L=4:

None found

Shuffled Z340, L=2:

[>t] [>t] [>t] [>t] (ALL EVEN POSITIONS)
9t [t9] [t9] 9t (ALL EVEN POSITIONS)

Shuffled Z340, L=3 and L=4:

None found

Z408, L=2, L=3, and L=4:

None found

————

So, based on the above:

1) Z340 favors cycles that fall on odd positions. Only two cycles were found that fall on even positions.
2) When Z340 is shuffled, the phenomenon is greatly diminished.
3) The phenomenon is completely absent from Z408.

This is really quite peculiar!

Perhaps #3 can be explained by the fact that Z408’s cycles are generally much longer than the ones from Z340.

(EDIT: Here’s the shuffled Z340 I used)

N;+2.lczX)k;KRV6+
p<T%CzcERB4-U.%LV
N>Ff+|S)Rc(7ppzlk
|.*^z)EOZVW*O^_K+
5&fBLXK95fBVBz+(@
Bp_56GH4HbH-ZWYjT
+K|t#WpdT|+JJly|4
p*F4SU>l(c)2GB^Ot
Y.*|lOpMp>Ry(T|<B
LB/+FZ)82B9+/2MMt
*.^V.OdR_A^WZcJ5P
8++B2FcBdU<5^d9K#
-+k+1>E|J+#9+tDFG
#5+lN3cD84T-W<YF+
ONAR5P2G*zLFOOHLU
<637yf+|RYjpPC+-F
VNyBC#&dl8ycGqSO:
24cFMDkM+(7SOM2K(
+|/Fp<CbU2zD1c+R+
1(CqzWMkbK;:p+GLz

OK – I ran another experiment:

Approach: Shuffle Z340 and look for sequences that have cycles of length 2. Check which ones fall entirely on even-numbered positions, and odd-numbered positions. Count them and compare to original Z340.

Results of 10,000 trials: https://docs.google.com/spreadsheets/d/ … sp=sharing

The average number of even-positioned cycles found in shuffles was about 2.8 (compare to 2 in the original Z340).
The average number of odd-positioned cycles found in shuffles was also about 2.8 (compare to 16 in the original Z340).

Of the 10,000 trials, 49 of them had 16 or more odd-positioned cycles. That works out to 0.5% of the trials. Or, saying it a different way: When Z340 is shuffled, there is a 0.5% chance of getting as many (or more) odd-positioned cycles as we find in the original Z340.

However, of the 10,000 trials, 5,815 of them had 2 or more even-positioned cycles (58.15% of the trials). When Z340 is shuffled, there is a 58.15% chance of getting as many (or more) even-positioned cycles as we find in the original Z340.

So, there does seem to be a strong bias in Z340 towards cycles in odd-numbered positions.

Weird!

Thank you for doing that. Your statistics seem significant. I also mentioned that 37, 38 and 41 all are unique to odd positions. It seems to me that finding an ABCABCABC that falls only on odd positions is not very likely. But with so many symbols with count of 3 or more, maybe it can happen. I will re-read your posts. It seems to me that Zodiac may have treated odds differently than he did evens. Thanks again.

Daikon, are you out there? This relates to your post at: viewtopic.php?f=81&t=2625&start=10.

I’m here. 🙂 I’m following everything you guys are doing. I’m just at a loss as far as what all this could mean. This odds/evens dichotomy is very peculiar indeed. Based on the number of bigram repeats, evens seem to carry a message (good number of bigram repeats) and odds seem to be just filler (almost no repeated bigrams). And yet when you looked at cycles, it seems to suggest the opposite: evens is filler (no strong cycles) and odds is the message (several strong cycles). Supposing both carry the message, but some sort of transposition was done to just even positions after the encoding (and not odds), which would destroy cycles in evens, but it should destroy bigram repeats too, but those are plentiful in evens. As far as odds, there is actually one scenario that can explain what we are seeing for odd positions: if you do a transposition *prior* to encoding, it would mostly destroy bigram repeats, but leave strong cycles present.

Could it be that evens have to be read vertically (by columns) and odds horizontally (by rows)? Or the other way around? I.e. intertwined, sort of like a lattice. Did you test for cycles for odds and evens read by columns, vertically?

The even/odd phenomenon is fascinating. Take a look at this diagram of repeating patterns:

On lines 6 and 19 you can find this repeating pattern:

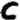
(Note also that those repeats are happening right where the "box corners" appear, those patterns involving the symbols ImageImageImageImage and Image)

On lines 12 and 14 you can find this repeating pattern:

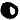
When you delete ALL odd-numbered positions from the cipher text, those patterns are perfectly preserved as repeating trigrams. And there are still many bigram repeats, as you’ve observed. When odds are deleted, 22% of the resulting 170-character cipher is covered by repeating bigrams, whereas the repeating bigram coverage is only 4.71% for the case of deleting evens.

Very interesting!

UPDATE: For contrast, here is the result for Z408:

When odds are deleted, 20% of the resulting 204-character cipher is covered by repeating bigrams, whereas the repeating bigram coverage is 25% for the case of deleting evens.

For future reference, here are the (webtoy alphabet) transcriptions of the different ciphers:

Z340 with odd positions deleted:

E>lVk1T2N+(ODY<K)
yc+ZW)#HSp^8Vp+R2
9+td5P&kpRFO*CF2(
5K%2cG.L(2f#+Nz@9
<++RFcA4-lV^+p<B-
+/t|YpTK2cR|54.&F
6S#N5B(8lF^54.Vt+
B1:9EVZ-|.zKO^fq2
c+1C+lB)+)CWPST(p
Fd<t_O*C>DNkzOAK+

Z340 with even positions deleted:

HRp^P|LGdpB#%W.*f
B:MUG(LzJp7l*3O+K
_Mzj|F+4/8^l-dk>D
#+q;UXVz|GJjO_Y+L
dMbZ2By6KzU+JO7Fy
UR5EDBbMO<lJ*TM+B
z9y+|Fc;RGNf2bc4+
yX*4C>U5+c3B(p.MG
RTL6<FW|L+WzcOH/)
|kW7BYB-cMHpSZ8|;

Cycle analysis:

Odds removed:
http://pastebin.com/npE7Q5V3

Evens removed:
http://pastebin.com/ddC6BjjH

(BTW I apologize if someone has posted this analysis already – I may have overlooked it!)

I’m here. I’m following everything you guys are doing. I’m just at a loss as far as what all this could mean. This odds/evens dichotomy is very peculiar indeed. Based on the number of bigram repeats, evens seem to carry a message (good number of bigram repeats) and odds seem to be just filler (almost no repeated bigrams). And yet when you looked at cycles, it seems to suggest the opposite: evens is filler (no strong cycles) and odds is the message (several strong cycles). Supposing both carry the message, but some sort of transposition was done to just even positions after the encoding (and not odds), which would destroy cycles in evens, but it should destroy bigram repeats too, but those are plentiful in evens. As far as odds, there is actually one scenario that can explain what we are seeing for odd positions: if you do a transposition *prior* to encoding, it would mostly destroy bigram repeats, but leave strong cycles present.

Could it be that evens have to be read vertically (by columns) and odds horizontally (by rows)? Or the other way around? I.e. intertwined, sort of like a lattice. Did you test for cycles for odds and evens read by columns, vertically?

I have not. I think that maybe Jarlve is working on something like that. It is looking like we may have to do a cycle analysis of the odds versus the evens in all directions. I wonder if anyone has done that before? It seems to me that encoding with paper and pencil, it would be easy to just skip spaces. Make a checkerboard. Then fill in the gaps in a different direction. I am thinking about the 5 symbols unique to odds and 9 symbols unique to evens, however. If the evens were the second half of the message, then would it be possible for that to happen if he used the same key throughout?