I updated the main post with information about our current direction.

Edit: I’m going to let my solver run on the 340 odds and evens through the night to start with.

@smokie,

I’d like to add our numbers table to the main post as well. Do you want to share the file? Or perhaps we can maintain it in google docs and share permissions between the contributors. I’m still working on the smokie8. I’ll let you know when I want to know more.

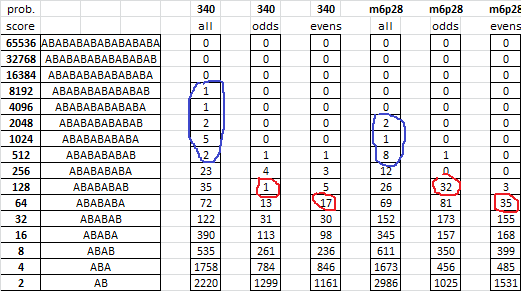
1) Z340 favors cycles that fall on odd positions. Only two cycles were found that fall on even positions.
2) When Z340 is shuffled, the phenomenon is greatly diminished.
3) The phenomenon is completely absent from Z408.

So, there does seem to be a strong bias in Z340 towards cycles in odd-numbered positions.

It seems amazing. But I feel a bit skeptic, could you please run the same test for smokie’s first cipher? smokie.txt

The reason why is because I believe it could be plaintext induced phenomenon. The 408 plaintext shows a better than average distribution for odds and evens (when considering even distribution of letters over odds and even positions). The smokie plaintext (the purple haze message) has a much worse than average distribution for odds and evens. And this reflects upon the cipher/encoding.

I’ve added some of your information/links/etc to the main post. If you want me to adjust or remove anything, let me know.

Could it be that evens have to be read vertically (by columns) and odds horizontally (by rows)? Or the other way around? I.e. intertwined, sort of like a lattice. Did you test for cycles for odds and evens read by columns, vertically?

It’s not conclusive but I have ran a test in that direction some time ago: grille variation.

Jarlve,

You are very disciplined. Now to m6p28. I believe that there are two keys, and they are highly cyclic. However, you may have randomized Key 2 some.

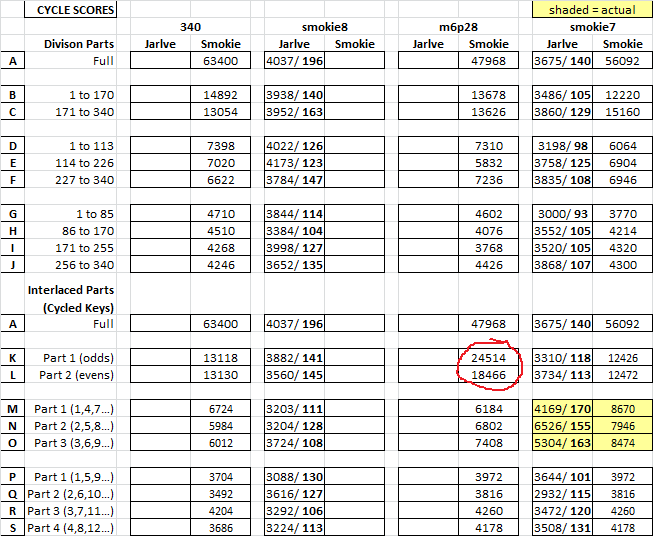
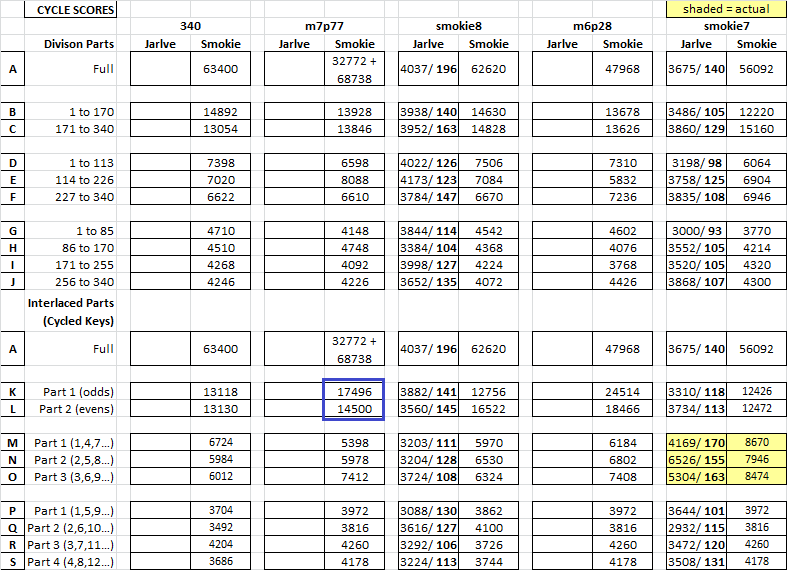
Also, here are more in depth cycle stats for Part 1 and Part 2. Although the two parts do not have many or any cycles at 512 or above, there are a lot of cycles scoring in the 256 or 128 range. Many more than with the 340 Parts 1 and 2, which accounts for the difference in scores between the 340 Parts 1 / 2 and m5p28 Part 1/ 2.

EDIT: I noticed that there are several very high scoring cycles when looking at the whole of m6p28. Interesting, and I wonder if, because I think that you used two keys, these are random.

EDITED PICTURE:

Part 1 has unique symbols: 24, 26, 29, 39, 54, 61.
Part 2 has unique symbols: 8, 16, 27, 34, 51, 52, 55, 58, 60, 62, 63.

I could not find any high scoring cycles where unique symbols cycled together in the same parts, as with the 340.

I read your grille analysis and am glad that you already did that. That makes me think more about the use of two keys, considering what has happened this last day. But I don’t know. I think that if we keep working on it, we can figure out what Zodiac did. I sent you a pm. I need a private email so that I can send an Excel file for the table. I will work on filling in smokie8 stats, and maybe figure out how to use Google Docs in the meantime.

Jarlve,

Here is the table with my scores for smokie8:

You are correct about m6p28, well done. I made an odds/evens cipher but increased the difficulty by adding a slight randomization to each part and by having a larger than usual number of symbols exclusive to each part. I was hoping that this would create false cycles to throw off your analysis.

Here is m7p77.txt. And it’s an interesting one. Difficulty rating 1-5, I’d say this is a 5. Just so you know, that you don’t have to spend weeks trying to figure it out.

Here are the solves for the 340 odds and evens from AZdecrypt99 (in development). These are low scoring solutions and it was the maximum score my 6-gram solver can achieve for these ciphers. I don’t believe anything is there.

340 odds:

Score: 21405 Ioc: 679 M: 341 C: 170 S: 58

oanewarlinssaddry
suchlartenisrulef
actsanemorestingu
sedthestaleslater
ichowstoftheelint
hatbushcluserices
tateanotallywhome
termighteousandcl
airoundaredtolook
andiststoconforat

HRp^P|LGdpB#%W.*f
B:MUG(LzJp7l*3O+K
_Mzj|F+4/8^l-dk>D
#+q;UXVz|GJjO_Y+L
dMbZ2By6KzU+JO7Fy
UR5EDBbMO<lJ*TM+B
z9y+|Fc;RGNf2bc4+
yX*4C>U5+c3B(p.MG
RTL6<FW|L+WzcOH/)
|kW7BYB-cMHpSZ8|;

340 evens:

Score: 20813 Ioc: 640 M: 317 C: 170 S: 54

malaysitlesfluent
whenitbutpreapert
herwasmyprofshots
andthedistobelich
eeerohinclarepeac
egroupinthroandmo
stblaaselorandare
asthmancodinfromt
heshelatethistisp
owerofshallyifine

E>lVk1T2N+(ODY<K)
yc+ZW)#HSp^8Vp+R2
9+td5P&kpRFO*CF2(
5K%2cG.L(2f#+Nz@9
<++RFcA4-lV^+p<B-
+/t|YpTK2cR|54.&F
6S#N5B(8lF^54.Vt+
B1:9EVZ-|.zKO^fq2
c+1C+lB)+)CWPST(p
Fd<t_O*C>DNkzOAK+

Here is a spreadsheet that shows all the counts for even- and odd-numbered positions for each cipher symbol, for Z340, Z408 and smokie.txt:

https://docs.google.com/spreadsheets/d/ … sp=sharing

It also includes divisibility tests for position numbers, for divisors from 3 to 20.

1) Z340 favors cycles that fall on odd positions. Only two cycles were found that fall on even positions.
2) When Z340 is shuffled, the phenomenon is greatly diminished.
3) The phenomenon is completely absent from Z408.

So, there does seem to be a strong bias in Z340 towards cycles in odd-numbered positions.

It seems amazing. But I feel a bit skeptic, could you please run the same test for smokie’s first cipher? smokie.txt

Here are the test results:

smokie.txt, L=2:

MP M [MP] [MP] [MP] [MP] 4 8.959601E-16 0.8888889 7.96409E-16 (ALL ODD POSITIONS)
M’ [M’] M [M’] [M’] [M’] 3 5.178649E-12 0.6666667 3.4524328E-12 (ALL ODD POSITIONS)
M[ [M[] M [M[] [M[] [M[] 3 5.178649E-12 0.6666667 3.4524328E-12 (ALL ODD POSITIONS)
#[ [#[] [#[] [[ 2 4.7892152E-9 0.6666667 3.1928102E-9 (ALL ODD POSITIONS)
M# [M#] [M#] MMM 2 7.483148E-9 0.5714286 4.276085E-9 (ALL ODD POSITIONS)
‘P [‘P] [‘P] P’ [‘P] 2 1.9156861E-8 0.5 9.5784305E-9 (ALL ODD POSITIONS)
‘[ [‘[] [‘[] [‘ [‘[] 2 1.9156861E-8 0.5 9.5784305E-9 (ALL ODD POSITIONS)

smokie.txt, L=3 and L=4:

None found

Shuffled smokie.txt, L=2, L=3 and L=4:

None found

Here’s the shuffled smokie.txt (I only tested one shuffle):

Q=V8-#_/!='0FE_S=
@WYARW8TQ.XEC%^G
6Q-BV-V40$/="B8H_
V7ASH@)<H8D9SN3@1
G61GL-34@JYVKN>,6
E]3]#I,1Q!*?.(TEL
10&!NON,>++"O)2T+
%3G-.."E.1FRABUPO
-Z:P.YK1_(9EF3EMJ
EJ/"8D!Z[8-GCNECA
45KKT3<Q>:21SG0R
4(UUQ2[CE@--)HXIM
:D:D8B3-D@-8[Q'D
?98,?GAQ%3FS506
-<[8E1-R&.YUP$Y!1
_?SEXL+,W&$XLZ3E3
-0I^Q=DT)]O4]X-%
HUM]IG6MJ'EPLEW$^
K%':C;XEME^JK1H-)
WQSE%OS(/(,<8GENI

What do those results say to you?

I imagine that if I did the 10,000 trials of random shuffles, the distribution of evens/odds will be very similar to my previous experiment on Z340 (viewtopic.php?p=41198#p41198), due to similar distribution of symbol frequencies.

I’ve added some of your information/links/etc to the main post. If you want me to adjust or remove anything, let me know.

Thanks for doing that. Nice to find all the info in one place!

Thanks doranchak,

It is much stronger in the 340 when it should actually be stronger in the smokie cipher. Perhaps 2 sets of plaintext letters were considered (consonants/vowels for instance) and each were given a different key but with some/many of the same symbols overlapping. And these sets had a bigger than average discrepancy between odds and evens.

If actual then we should find cycles within cycles, so to say. We could try to separate them by identifying/guessing strong many-symbol cycles within cycles and work our way down.

Look at this 4-symbol cycle my program found: |BOBcO| Oc|OBcOB|BOc|B|BccB|cBOcB|cO |BOBcO|

How is it possible for a string like "|BOBcO|" to form/repeat? It’s a pattern within a cycle that doesn’t cycle, because "B", "O" and "|" are repeated twice. My feelings are that this may point in the direction of cycles within cycles.

Thanks for m7p77. I have started working on it and will continue to adapt my system.

In response to my own post,

I think it may be more likely that my program crossed 2 actual cycles with: |BOBcO|Oc|OBcOB|BOc|B|BccB|cBOcB|cO|BOBcO|

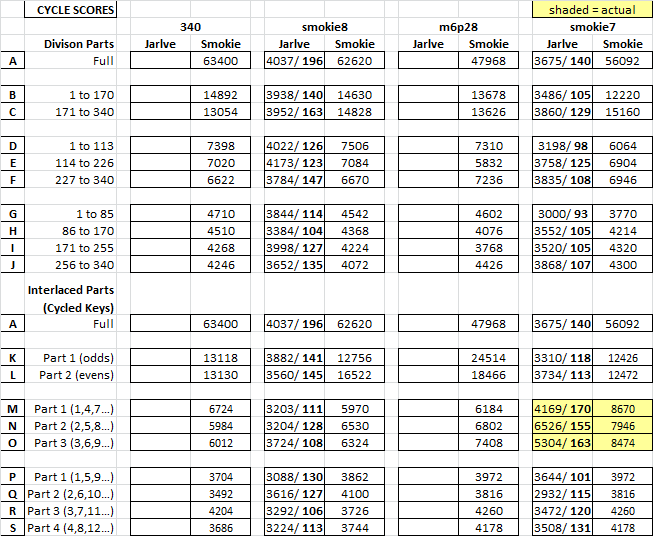
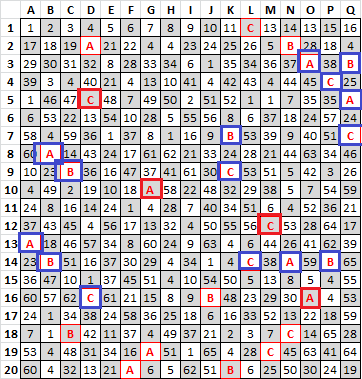
Well it looks to me like m7p77 has two keys. There is minimal evidence of cycling in three or four parts.

For odds, it looks like 12, 20 and 27 cycle together. There are a few 12’s and 20’s conveniently located in Part 2 to make for a very improbable cycle in the whole, making the cycle score for the whole extraordinarily high. That is why I broke out the score into two: 32772 + 68738.

A=20, B=27, C=12. The odds are boxed blue, and the conveniently located symbols are boxed in red, making for a very improbable CACACACACACACACA.

For Part 2, it looks like 1 and 8 probably cycle together. And probably 28 and 51. Most likely 6, 38 and 45 cycle together.

Part 1 has unique symbols: 43, 44, 49, and 52. The counts for these symbols are all at 3, making this not improbable even if there was one key.

Part 2 has unique symbols 14, 15, 25, 38, and 45. The counts for these symbols are between 2 and 4, and I don’t think that this is so improbable for a one key message either. That would be like basically flipping a coin four times and getting heads four times. However, symbol 14 cycles with 38, but not perfectly. 38 and 45 cycle perfectly. For two symbols of count 4 to each land on all odd numbered positions and also cycle together seems fairly improbable to me.

But is that true? Seems like that would be ABABABAB, so that would be (.5)(.5)^8=1/65,536. But there are a lot of other symbols that could fall together that way.

I noticed that the 12 – 20 – 27 cycle in the odds is randomized at the beginning and the end. Also, the cycle scores for the middle one third of the whole seems higher than for the first and last one third of the whole, making me think that you may have randomized some of your cycles this way. Compare D, E and F.

The big discrepancy between K and L is because of one or two very high scoring cycles between 12 and 20 and 20 and 27 I think.

I did see some cycling in Part 3 of a four key cipher, but at that level I don’t know yet how to interpret the numbers. They are so low… it is difficult for me to know what to make of them. There were a few at the 64 score range, which was higher than Parts 1, 2 and 4.

I’m experimenting with something similar to doranchak’s brute force search for homophone sequences to investigate the cycles in the 340 and other ciphers. My system does not count sub-string repeats but rather if a sub-string has no repeating symbols. This may allow the spotlight on different kind of cycles found in the 340. For instance morphological homophone sequences like "ABCABCCBACBA". I don’t think very highly of it at the moment but I wanted to do something different.

Top 10 list for 2 to 7-symbol cycles in the 340.

Legend:
Ws: weighted score.
C: length of the cycle string.
ApL: alternations per length. (an ApL of 1 is a perfect cycle)

Perhaps 2 sets of plaintext letters were considered (consonants/vowels for instance) and each were given a different key but with some/many of the same symbols overlapping.

Different keys for consonants/vowels is an interesting idea. But I don’t think it would be possible to decipher even if you have the keys. For example, consider the following ciphertext: AAAAAA. How would you know which key to use for the first A if you don’t know if it’s a consonant or a vowel? Or for the second A? And so forth. Although I’ve long suspected that Z might have messed up and created an encryption scheme that’s undecipherable even if the key(s) are known. Considering he didn’t "proofread" Z408 either, leaving several mistakes and typos uncorrected. He might have even realized that Z340 was a dud later on, but was too embarrassed to admit it, and decided to proclaim that he was "crackproof" instead. Although, perhaps, we’ll be able to use computers to arrive at the correct solution to his truly uncrackable cipher, and embarrass Z in the process as well. 🙂

How is it possible for a string like "|BOBcO|" to form/repeat? It’s a pattern within a cycle that doesn’t cycle, because "B", "O" and "|" are repeated twice. My feelings are that this may point in the direction of cycles within cycles.

Those sorts of patterns seem to be very common. Here is a small excerpt from an experiment I just ran:

Score, Alphabet Combination, Sequence that repeats, Full sequence and matches
6.507705E-8, MRl|, M|Rl|MRl, Rl|MlR M|Rl|MRl R|MlR| M|Rl|MRl ||M|
6.561267E-8, #BEl, #BlBEBlB, ElB#B#ll# #BlBEBlB #BlBEBlB BB
6.615269E-8, 2Rfz, 2fzR2zR2, R 2fzR2zR2 2z 2fzR2zR2 RzRf2zf2Rzz
6.642605E-8, <Bpq, pq<Bp<BB, ppB<Bppp pq<Bp<BB p<BBBB pq<Bp<BB p
6.642605E-8, <Bpq, q<Bp<BBp, ppB<Bpppp q<Bp<BBp <BBBBp q<Bp<BBp
6.6666665E-8, NOP|, O|PO|ONO, P|NO O|PO|ONO |O|N|N| O|PO|ONO |
6.6666665E-8, NOP|, |PO|ONO|, P|NOO |PO|ONO| O|N|N|O |PO|ONO|
6.802721E-8, <FUl, FFlFU<Fl, l<Ul FFlFU<Fl U<FU<l FFlFU<Fl F<
6.802721E-8, <FUl, lFFlFU<F, l<U lFFlFU<F lU<FU< lFFlFU<F lF<
6.802721E-8, Fbl, FFlFbFlF, ll FFlFbFlF bl FFlFbFlF
6.802721E-8, MOP|, M|PO|OMO, P|OMO M|PO|OMO |MO|M||O M|PO|OMO |
6.802721E-8, MOP|, OM|PO|OM, P|OM OM|PO|OM O|MO|M|| OM|PO|OM O|
6.9122805E-8, 25Nz, 2Nz2z525, 2Nz2z525 2z 2Nz2z525 zN5N525z2zNz
6.941552E-8, *Ml|, M|l*|Ml|, l|*Ml* M|l*|Ml| Ml|* M|l*|Ml| |*M|
6.944445E-8, &BF|, F|FBFB|, |BB|F&F F|FBFB| B|&B F|FBFB| BFB||FBB|
6.944445E-8, )BF|, F|FBFB|, |B)B)|FF F|FBFB| B|B F|FBFB| BFB|)))|FBB|
6.944445E-8, 3BF|, F|FBFB|, |BB3|FF F|FBFB| B|B F|FBFB| 3BFB||FBB|
6.944445E-8, >OV|, >V|OVO|O, >V|OVO|O >V|OVO|O ||V>V|O|O|O>O|
6.944445E-8, BFH|, F|FBFB|, H|BBH|FF F|FBFB| B|B F|FBFB| BFB|H|FBBH|
6.944445E-8, BFP|, F|FBFB|, P|BB|FPF F|FBFB| B|B F|FBFB| BFB|P|FBB|
6.944445E-8, BFT|, F|FBFB|, |TBB|FF F|FBFB| BT|TB F|FBFB| BTFB|T|FBB|
6.944445E-8, BFW|, F|FBFB|, |BWBW|FF F|FBFB| B|B F|FBFB| BFWB|WW|FWBB|
6.944445E-8, BFk|, F|FBFB|, k|BB|FkFk F|FBFB| B|B F|FBFB| BFB||FkBBk|
6.944445E-8, BF|, F|FBFB|, |BB|FF F|FBFB| B|B F|FBFB| BFB||FBB|

Yours:
6.944445E-8, BOc|, |BOBcO|, |BOBcO| Oc|OBcOB|BOc|B|BccB|cBOcB|cO |BOBcO|

6.944445E-8, OVZ|, V|OZVO|O, V|OZVO|O V|OZVO|O ||VVZ|O|O|OZO|
6.944445E-8, OVct, VOcVOtOc, VOcVOtOc VOcVOtOc ccVtVcOccOtOcO
6.944445E-8, OVt|, V|OVOt|O, V|OVOt|O V|OVOt|O ||VtV|O|O|tOO|
7.117802E-8, &-MR, RMRM&R-MR, RMRM&R-MR — RMRM&R-MR -M
7.117802E-8, &CMR, RMRM&RCMR, RMRM&RCMR RMRM&RCMR CCCM
7.142857E-8, FOXl, FXOFlOFO, lOlOFFlO FXOFlOFO lFFl FXOFlOFO O
7.14449E-8, 2BFz, 2FBzFBB, 2BBz2zFFF22z2z 2FBzFBB 2BFzFBF2BzB 2FBzFBB z
7.246478E-8, &.Bp, p.BpBBp, ppB.Bppp& p.BpBBp .&BB.B.B p.BpBBp
7.246478E-8, .3Bp, p.BpBBp, ppB.Bpp3p p.BpBBp .BB.B.3B p.BpBBp
7.246478E-8, .:Bp, p.BpBBp, , ppB.B:ppp p.BpBBp .BB.B:.B p.BpBBp
7.246478E-8, .Bp, p.BpBBp, , ppB.Bppp p.BpBBp .BB.B.B p.BpBBp
7.246478E-8, 7Bpq, pqBp7BBp, , ppBBpp7p pqBp7BBp BBBB pqBp7BBp
7.2886294E-8, )>Fl, lFFlF>Fl, , >l)) lFFlF>Fl F lFFlF>Fl )))F>
7.2886294E-8, )FZl, lFFlFZFl, , l)Z) lFFlFZFl F lFFlFZFl )))FZ
7.2886294E-8, 7>Fl, lFFlF>Fl, , >l7 lFFlF>Fl 7F lFFlF>Fl F7>
7.2886294E-8, 7FZl, lFFlFZFl, , lZ7 lFFlFZFl 7F lFFlFZFl F7Z
7.2886294E-8, 9FMl, FlF9MFlF, , lMl9MF FlF9MFlF MlMF9 FlF9MFlF M
7.2886294E-8, >AFM, MMFFF>MF, , > MMFFF>MF AF MMFFF>MF F>MA
7.2886294E-8, >FHl, lFFlF>Fl, , H>lH lFFlF>Fl F lFFlF>Fl HF>H
7.2886294E-8, >FKM, MFFF>KMF, , >KMK MFFF>KMF KFMK MFFF>KMF F>MK

I made my spreadsheet shuffle the 340 every time I click on "calculate now." I clicked about 20 times before I got one ABABABAB and all other A’s and B’s on odds. Then I clicked 100 times and got nothing so far.

I was wondering, if you haven’t already answered my question (maybe you have), how many time to shuffle the 340 before getting an ABCABCABC and some other random A’s, B’s or C’s where all are on either odds or evens?

On a hunch I also tried to expand the evens in the first half, and the odds in the second half. I think that maybe he treated odds and evens differently, and also the top half and the bottom half differently. With Jarlve’s program I did get some solutions over 25,000. But I only tried a few times. I did get this:

yunforofplayedthe
nosedingcamerinth
eirmisedtothemake
coveralifivesofth
avisanalactionali
veforangleverthed
iconinthemaybeaba
dthegamesandhowev
eristsofareminist
sareforeseverthis
lowinglandsorthtr
acountarangherist
himastrongledthew
astrongsaredbygro
securrybackblongr
adewasthemouthisa
wonofusecolawentf
ortwehadpractitio
nthewingsaresided
thecomebasedintho

But it’s mostly gibberish. I didn’t expand the odds in the first half and the evens in the second half. I had to mess around with that because it was mindless activity and I needed a rest. I will also work on trying to figure out if he treated the two halves differently with respect to odds and evens later. Maybe I will mess around with that a little and then make a new message for Jarlve if he wants one.

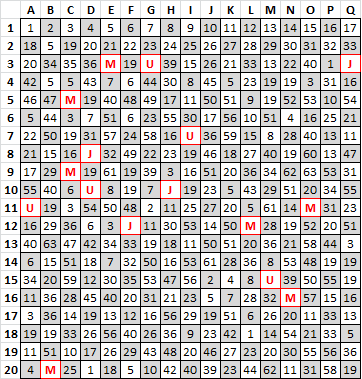
Anyway, 37, 38 and 41 ( M U J ) all cycle at the top half. On the bottom half, they do not but still sit at odd numbered positions.

Perhaps this is a clue as to what he did with the bottom half.

I thought that maybe snaking the odd numbered rows backwards, because that would make 37, 38 and 41 cycle better in the bottom half. And maybe that would explain the discrepancy regarding bigram repeats? But only on odd numbered rows, right?

That is as much as I have done. Did he rearrange the bottom half so that 37, 38 and 41 would not move from odd numbered positions? Or did he just randomize the symbol selection?