I was wondering, if you haven’t already answered my question (maybe you have), how many time to shuffle the 340 before getting an ABCABCABC and some other random A’s, B’s or C’s where all are on either odds or evens?
I will run this test ASAP.
OK I ran a shuffle test that just looks for "ABCABCABC" patterns (no matter where it appears in the sequence – I only care that it is contiguous), where every letter in the contiguous repeats as well as the leftover letters fall on all even or all odd numbered positions.
Number of shuffles, sequence
233 9 /9E /9E /9E (ALL ODD POSITIONS)
105 /6E /6E /6E (ALL EVEN POSITIONS)
4 -T- -T/ -T/ -T/ T (ALL EVEN POSITIONS)
66 YPS YPS YPS YS (ALL ODD POSITIONS)
203 dkkf fkd fkd fkd d (ALL ODD POSITIONS)
159 E68 E68 E68 8 (ALL EVEN POSITIONS)
63 **^^*^9 *9^ *9^ *9^ (ALL EVEN POSITIONS)
22 >C EC> EC> EC> C (ALL ODD POSITIONS)
22 H /HP /HP /HP (ALL ODD POSITIONS)
18 .C/ .C/ .C/ C…C (ALL ODD POSITIONS)
97 –.).). ).- ).- ).- (ALL EVEN POSITIONS)
94 bDH bDH bDH DH (ALL EVEN POSITIONS)
21 VV V-E V-E V-E -V- (ALL EVEN POSITIONS)
6 /t- /t- /t- -t- (ALL ODD POSITIONS)
187 D* *DH *DH *DH **H (ALL EVEN POSITIONS)
194 Zf 1fZ 1fZ 1fZ (ALL ODD POSITIONS)
124 Db7 Db7 Db7 D (ALL ODD POSITIONS)
Total shuffles: 1618
Hits: 17
Average shuffles per hit: 95.1765
I made my spreadsheet shuffle the 340 every time I click on "calculate now." I clicked about 20 times before I got one ABABABAB and all other A’s and B’s on odds. Then I clicked 100 times and got nothing so far.
OK I did this experiment too. Shuffled and looked for L=2 sequences, with 4 repetitions in a row, where all letters in the full sequence (including leftovers) fall on all even numbered positions or all odd numbered positions:
Number of shuffles, full sequence
114 HD HD HD HD (ALL ODD POSITIONS)
17 D8 D8 D8 D8 (ALL ODD POSITIONS)
1 dH dH dH dH d (ALL EVEN POSITIONS)
11 – -f -f -f -f (ALL ODD POSITIONS)
21 Y> Y> Y> Y> (ALL ODD POSITIONS)
38 Cd Cd Cd Cd Cd (ALL ODD POSITIONS)
11 T TS TS TS TS (ALL EVEN POSITIONS)
66 tS tS tS tS (ALL EVEN POSITIONS)
19 H> H> H> H> (ALL ODD POSITIONS)
2 kD kD kD kD k (ALL EVEN POSITIONS)
33 44) )4 )4 )4 )4 (ALL EVEN POSITIONS)
26 >H >H >H >H (ALL ODD POSITIONS)
88 k kN kN kN kN N (ALL ODD POSITIONS)
19 # #> #> #> #> (ALL ODD POSITIONS)
82 9t 9t 9t 9t (ALL ODD POSITIONS)
11 8S 8S 8S 8S (ALL ODD POSITIONS)
65 JS JS JS JS (ALL ODD POSITIONS)
26 ^> ^> ^> ^> ^^ (ALL EVEN POSITIONS)
8 Jd Jd Jd Jd d (ALL EVEN POSITIONS)
1 >- >- >- >- – (ALL EVEN POSITIONS)
16 t9 t9 t9 t9 (ALL EVEN POSITIONS)
27 >f >f >f >f (ALL ODD POSITIONS)
7 *8 *8 *8 *8 ** (ALL ODD POSITIONS)
27 YH YH YH YH (ALL EVEN POSITIONS)
121 N NS NS NS NS (ALL ODD POSITIONS)
27 G8 G8 G8 G8 GG (ALL EVEN POSITIONS)
64 WT TW TW TW TW W (ALL ODD POSITIONS)
18 >Y >Y >Y >Y (ALL ODD POSITIONS)
57 SD SD SD SD (ALL EVEN POSITIONS)
41 T> T> T> T> T (ALL ODD POSITIONS)
8 Zf Zf Zf Zf (ALL ODD POSITIONS)
115 .H .H .H .H .. (ALL ODD POSITIONS)
10 U U* U* U* U* ** (ALL EVEN POSITIONS)
7 y yY yY yY yY (ALL ODD POSITIONS)
18 t9 t9 t9 t9 (ALL EVEN POSITIONS)
1 .k .k .k .k . .k (ALL ODD POSITIONS)
18 D) D) D) D) ) (ALL ODD POSITIONS)
32 Sf Sf Sf Sf (ALL ODD POSITIONS)
40 T T> T> T> T> (ALL EVEN POSITIONS)
38 ( (t (t (t (t (( (ALL EVEN POSITIONS)
26 GC GC GC GC GC G (ALL EVEN POSITIONS)
4 Hf Hf Hf Hf (ALL ODD POSITIONS)
20 ZV ZV ZV ZV VV (ALL EVEN POSITIONS)
32 D> D> D> D> (ALL ODD POSITIONS)
22 TY TY TY TY T (ALL ODD POSITIONS)
32 >S >S >S >S (ALL EVEN POSITIONS)
9 ZD ZD ZD ZD (ALL ODD POSITIONS)
11 Z9 Z9 Z9 Z9 (ALL EVEN POSITIONS)
88 8) 8) 8) 8) ) (ALL ODD POSITIONS)
2 T TY TY TY TY (ALL ODD POSITIONS)
2 ZY ZY ZY ZY (ALL EVEN POSITIONS)
30 H8 H8 H8 H8 (ALL EVEN POSITIONS)
12 C CJ CJ CJ CJ (ALL EVEN POSITIONS)
6 <J <J <J <J << (ALL ODD POSITIONS)
115 H> H> H> H> (ALL EVEN POSITIONS)
53 VK VK VK VK KKKVV (ALL ODD POSITIONS)
10 DS DS DS DS (ALL ODD POSITIONS)
6 8> 8> 8> 8> (ALL EVEN POSITIONS)
37 tS tS tS tS (ALL EVEN POSITIONS)
40 f# f# f# f# # (ALL EVEN POSITIONS)
10 y yl yl yl yl lll (ALL ODD POSITIONS)
3 U UJ UJ UJ UJ (ALL ODD POSITIONS)
17 R R# R# R# R# R R# R (ALL EVEN POSITIONS)
6 G Gf Gf Gf Gf G (ALL ODD POSITIONS)
21 Y9 Y9 Y9 Y9 (ALL EVEN POSITIONS)
39 S# S# S# S# # (ALL EVEN POSITIONS)
5 GG Gf Gf Gf Gf (ALL EVEN POSITIONS)
30 HT HT HT HT T (ALL EVEN POSITIONS)
30 C Cf Cf Cf Cf (ALL ODD POSITIONS)
3 89 89 89 89 (ALL EVEN POSITIONS)
29 (k (k (k (k (( (k (ALL EVEN POSITIONS)
4 f> f> f> f> (ALL EVEN POSITIONS)
11 yGG Gy Gy Gy Gy (ALL EVEN POSITIONS)
63 Ly yL yL yL yL L (ALL EVEN POSITIONS)
19 Sf Sf Sf Sf (ALL ODD POSITIONS)
40 *- * *- *- *- *- (ALL EVEN POSITIONS)
34 8Y 8Y 8Y 8Y (ALL ODD POSITIONS)
43 kS kS kS kS k (ALL ODD POSITIONS)
11 V VU VU VU VU UV (ALL ODD POSITIONS)
72 .U .U .U .U . .U (ALL ODD POSITIONS)
6 >9 >9 >9 >9 (ALL ODD POSITIONS)
2 Yt Yt Yt Yt (ALL ODD POSITIONS)
6 ** *Z *Z *Z *Z (ALL ODD POSITIONS)
7 JH JH JH JH (ALL EVEN POSITIONS)
41 kt kt kt kt k (ALL EVEN POSITIONS)
58 d d> d> d> d> (ALL ODD POSITIONS)
24 JY JY JY JY (ALL EVEN POSITIONS)
10 Z8 Z8 Z8 Z8 (ALL ODD POSITIONS)
23 555 5t 5t 5t 5t (ALL EVEN POSITIONS)
5 Ny Ny Ny Ny Ny (ALL EVEN POSITIONS)
42 -9 -9 -9 -9 – (ALL EVEN POSITIONS)
3 # #D #D #D #D (ALL EVEN POSITIONS)
50 Z8 Z8 Z8 Z8 (ALL EVEN POSITIONS)
8 G GS GS GS GS G (ALL ODD POSITIONS)
47 9> 9> 9> 9> (ALL EVEN POSITIONS)
51 S# S# S# S# # (ALL ODD POSITIONS)
86 UZ UZ UZ UZ U (ALL EVEN POSITIONS)
19 -l -l -l -l lll- (ALL ODD POSITIONS)
61 dU dU dU dU dU (ALL EVEN POSITIONS)
20 4 4t 4t 4t 4t 4 (ALL ODD POSITIONS)
38 M MZ MZ MZ MZ MM (ALL ODD POSITIONS)
67 8C 8C 8C 8C C (ALL EVEN POSITIONS)
14 tf tf tf tf (ALL EVEN POSITIONS)
8 (T (T (T (T T((( (ALL ODD POSITIONS)
2 -S -S -S -S – (ALL ODD POSITIONS)
53 UC UC UC UC UC (ALL ODD POSITIONS)
11 C Ct Ct Ct Ct (ALL ODD POSITIONS)
114 HS HS HS HS (ALL EVEN POSITIONS)
99 M MW MW MW MW WWMM (ALL EVEN POSITIONS)
54 SZ SZ SZ SZ (ALL EVEN POSITIONS)
36 kS kS kS kS k (ALL ODD POSITIONS)
24 l lT l lT lT lT lT (ALL EVEN POSITIONS)
40 # #Z #Z #Z #Z (ALL ODD POSITIONS)
4 SH SH SH SH (ALL ODD POSITIONS)
160 )S )S )S )S ) (ALL ODD POSITIONS)
33 >8 >8 >8 >8 (ALL ODD POSITIONS)
34 DZ DZ DZ DZ (ALL ODD POSITIONS)
35 >D >D >D >D (ALL ODD POSITIONS)
21 t9 t9 t9 t9 (ALL ODD POSITIONS)
26 J8 J8 J8 J8 (ALL EVEN POSITIONS)
3 Y- Y- Y- Y- – (ALL EVEN POSITIONS)
23 <M <M <M <M <M <M M (ALL ODD POSITIONS)
8 D< D< D< D< << (ALL ODD POSITIONS)
14 8y 8y 8y 8y y (ALL EVEN POSITIONS)
7 JL JL JL JL LL (ALL EVEN POSITIONS)
50 tf tf tf tf (ALL EVEN POSITIONS)
26 Z4 Z4 Z4 Z4 44 (ALL ODD POSITIONS)
14 KJ KJ KJ KJ KKK (ALL EVEN POSITIONS)
54 8J 8J 8J 8J (ALL EVEN POSITIONS)
1 >Y >Y >Y >Y (ALL EVEN POSITIONS)
1 DJ DJ DJ DJ (ALL ODD POSITIONS)
12 # #Z #Z #Z #Z (ALL ODD POSITIONS)
23 *C C* C* C* C* * (ALL ODD POSITIONS)
34 *G *G *G *G G* *G (ALL EVEN POSITIONS)
7 >8 >8 >8 >8 (ALL EVEN POSITIONS)
19 VV VZ VZ VZ VZ (ALL ODD POSITIONS)
11 2 2U 2U 2U 2U 222 2U (ALL EVEN POSITIONS)
70 U U> U> U> U> (ALL EVEN POSITIONS)
16 )9 )9 )9 )9 ) (ALL ODD POSITIONS)
9 S8 S8 S8 S8 (ALL EVEN POSITIONS)
138 .. .C .C .C .C C (ALL ODD POSITIONS)
9 -Y -Y -Y -Y – (ALL ODD POSITIONS)
89 ZH ZH ZH ZH (ALL EVEN POSITIONS)
100 .C .C .C .C .C . (ALL ODD POSITIONS)
12 >Y >Y >Y >Y (ALL EVEN POSITIONS)
17 )^ )^ )^ )^ ^ )^ (ALL ODD POSITIONS)
79 9f 9f 9f 9f (ALL ODD POSITIONS)
29 HS HS HS HS (ALL ODD POSITIONS)
89 Yd Yd Yd Yd d (ALL EVEN POSITIONS)
36 d dT dT dT dT T (ALL EVEN POSITIONS)
30 WD WD WD WD WW (ALL EVEN POSITIONS)
1 SY SY SY SY (ALL EVEN POSITIONS)
59 9# 9# 9# 9# # (ALL ODD POSITIONS)
7 W W9 W9 W9 W9 W (ALL EVEN POSITIONS)
20 WW# #W #W #W #W (ALL ODD POSITIONS)
36 YC YC YC YC C (ALL EVEN POSITIONS)
29 ZS ZS ZS ZS (ALL ODD POSITIONS)
12 S) S) S) S) ) (ALL ODD POSITIONS)
82 9J 9J 9J 9J (ALL ODD POSITIONS)
2 tf tf tf tf (ALL EVEN POSITIONS)
7 k kC kC kC kC C (ALL ODD POSITIONS)
1 fD fD fD fD (ALL ODD POSITIONS)
73 S9 S9 S9 S9 (ALL ODD POSITIONS)
97 d) d) d) d) d) (ALL EVEN POSITIONS)
21 NU NU NU NU UN (ALL EVEN POSITIONS)
45 >t >t >t >t (ALL ODD POSITIONS)
48 ZD ZD ZD ZD (ALL ODD POSITIONS)
69 ^^ ^D ^D ^D ^D (ALL ODD POSITIONS)
3 kN kN kN kN kN (ALL ODD POSITIONS)
65 J* J* J* J* ** (ALL ODD POSITIONS)
77 t9 t9 t9 t9 (ALL EVEN POSITIONS)
18 f8 f8 f8 f8 (ALL ODD POSITIONS)
2 LN NL NL NL NL L (ALL ODD POSITIONS)
38 ND ND ND ND N (ALL ODD POSITIONS)
47 (t (t (t (t ((( (ALL EVEN POSITIONS)
14 8N 8N 8N 8N N (ALL EVEN POSITIONS)
128 ppppW Wp Wp Wp Wp Wp pp (ALL ODD POSITIONS)
6 9J 9J 9J 9J (ALL ODD POSITIONS)
21 < <* <* <* <* <* * (ALL ODD POSITIONS)
22 9Z 9Z 9Z 9Z (ALL ODD POSITIONS)
14 f) f) f) f) ) (ALL EVEN POSITIONS)
56 d9 d9 d9 d9 d (ALL ODD POSITIONS)
8 H> H> H> H> (ALL EVEN POSITIONS)
28 DY DY DY DY (ALL EVEN POSITIONS)
4 8t 8t 8t 8t (ALL ODD POSITIONS)
18 tf tf tf tf (ALL ODD POSITIONS)
20 Ht Ht Ht Ht (ALL EVEN POSITIONS)
Total shuffles: 6068
Hits: 187
Average shuffles per hit: 32.4492
@doranchak, thanks for running the cycle pattern test. How does this compare?
@smokie, I’m still working on your last cipher so at the moment I don’t need a new one. Do I need to give away the scheme of m7p77?
In-depth cycle analysis of the smokie8 (in comparison to the 340 and the 408) part 1:
Note that for my system the string "AB" is a perfect 2-symbol cycle and that "ABCA" is a perfect 3-symbol cycle, etc.
Perfect 2-symbol cycles:
340: 77 with an average length of 5.64 (unlikely length)
408: 36 with an average length of 10.52
smokie8: 48 with an average length of 5.35 (unlikely length)
Perfect 3-symbol cycles:
340: 45 with an average length of 7.13 (high count, unlikely length)
408: 4 with an average length of 17.5
smokie8: 18 with an average length of 5.83 (low length)
Perfect 4-symbol cycles:
340: 6 with an average length of 8.16 (unlikely length)
408: 0, runner up is Cpl 0.94: 1 with a length of 20 (actual)
smokie8: 2 with an average length of 7 (unlikely length)
Perfect 5-symbol cycles:
340: 0, runner up is Cpl 0.85: 3 with an average length of 15.66 (unlikely length)
408: 0, runner up is Cpl 0.89: 1 with a length of 32 (actual)
smokie8: 0, runner up is Cpl 0.80: 1 with a length of 9 (unlikely length)
Perfect 6-symbol cycles:
340: 0, runner up is Cpl 0.71: 2 with an average length of 15.5 (unlikely length)
408: 0, runner up is Cpl 0.78: 1 with an average length of 37 (actual)
smokie8: 0, runner up is Cpl 0.62: 1 with a length of 13 (unlikely length)
Perfect 7-symbol cycles:
340: 0, runner up is Cpl 0.6: 2 with an average length of 21 (unlikely length)
408: 0, runner up is Cpl 0.68: 2 with an average length of 43.5
smokie8: 0, runner up is Cpl 0.5: 10 with an average length of 15.2 (unlikely length)
Abbreviations (some will be for part 2):
Ws: weighted score.
C: cycle length.
Cpl: cycles per cycle length. A Cpl of 1 is a perfect cycle, lower is worse.
Pd1: percentual difference from expected cycle length.
O/E: odd/even position distribution.
There seem to be no likely many-symbol cycles in the 340 and the smokie8. There are much more 2, 3 and 4-symbol cycles in the 340 than in the 408 but they are mostly very short. An artifact of cycle randomization or altered encoding process? It’s also happening in the smokie8 but to quite a lesser degree. Cycles in the smokie8 are of diminished quality. I haven’t found any likely discrepancies in the parts analysis for the smokie8 so I believe that it’s something that is uniform/gradual/well spread. Perhaps I need to look at cycles which have a likely length and look for patterns.
@doranchak, thanks for running the cycle pattern test. How does this compare?
…
Note that for my system the string "AB" is a perfect 2-symbol cycle and that "ABCA" is a perfect 3-symbol cycle, etc.
I’m having trouble comparing because I don’t yet understand your methodology. Can you give an example of how you count perfect 2-symbol cycles? Does it mean "no leftover symbols"?
Doranchak: Thanks for doing that. It sounds like there is about a 99% chance that the MUJ cycle is a clue and 1% chance that it is a statistical anomaly. When you take into consideration that seven count of the MUJ group are not included as part of the cycle but still fall on exclusively odds positions, it makes this seem even more like a clue. I have been staring at cycles for about two years total so that is nice to see.
Jarlve: I will keep working on my system for a little while before you show m7p77. I know how I encoded smokie8 and this is indeed very interesting. They are an analysis of the whole, correct? What is a perfect cycle? One with no extra symbols? How many repeats?
I meant, how does your pattern test (for "|BOBcO|" etc) compare with other ciphers. ![]()
Anyway, currently I count like this:
For cycle string "ABCABCABC":
ABC=1, BCA=1, CAB=1, ABC=1, BCA=1, CAB=1, ABC=1
Counts=6, Counts_score=6
Cpl=Counts_score/Counts
Cycle_string_length=9, Cpl_weight=3
Weighted_score=Cycle_string_length*Cpl^Cpl_weight
9=Weighted_score
For cycle string "ABCCBAABC":
ABC=1, BCC=0, CCB=0, CBA=1, BAA=0, AAB, ABC=1
Counts=7, Counts_score=3
…
0.7=Weighted_score
For cycle string "ABABABA":
AB=1, BA=1, AB=1, BA=1, AB=1, BA=1
Counts=6, Counts_score=6
…
7=Weighted_score
As you can see it’s very simple at the moment, I’m thinking of adding something else (and perhaps I can just multiply by Counts instead of Cycle_string_length). I usually adjust the Cpl_weight until the the average cycle string length in my top results list is about the expected value. For instance in the 340 a 3-symbol cycle should have an expected total length of about 16 (340/63*3).
I’ve taken a closer look at your list and I really like how you used cosine similarity to come up with the correct 7-symbol cycle in the 408.
Jarlve: I will keep working on my system for a little while before you show m7p77. I know how I encoded smokie8 and this is indeed very interesting. They are an analysis of the whole, correct? What is a perfect cycle? One with no extra symbols? How many repeats?
Yes, analysis of the whole. Some examples of perfect cycles for my current system "AB", "ABA", "ABC", "ABCA", "ABCD", "ABCDABCD", "ABCDEAB".
I meant, how does your pattern test (for "|BOBcO|" etc) compare with other ciphers.
Oh! My guess is that the same kinds of patterns happen all over the place. I’m fairly confident they would appear frequently even in shuffled texts.
Here’s a sampling from Z408:
1.5205266E-11, KOjq, qqOqqKqOqq, OK qqOqqKqOqq KqqjOKO qqOqqKqOqq
1.5205266E-11, KOq, qqOqqKqOqq, OK qqOqqKqOqq KqqOKO qqOqqKqOqq
1.5522044E-11, 5U^q, q5Uq^qq5qq, Uq^U q5Uq^qq5qq U^qq5U5^5U5U^Uq q5Uq^qq5qq U
1.5615304E-11, PUck, PUkPUkPUkcP, PUk PUkPUkPUkcP Ukc PUkPUkPUkcP cUcPcPUk
1.8626451E-11, 5KUq, q5UqqKq5qq, UKqU q5UqqKq5qq UKqq5U55UK5UUq q5UqqKq5qq U
1.8738367E-11, PUk, PUkPUkPUkP, PUk PUkPUkPUkP Uk PUkPUkPUkP UPPUk
1.9557342E-11, 9PU, 9PU9PU9PU9, 9PU9PU9PU9 PU 9PU9PU9PU9 PU9P99U99PP9U
1.9557342E-11, 9PUj, 9PU9PU9PU9, 9PU9PU9PU9 PU9PjU 9PU9PU9PU9 P99U99PP9U
1.9868215E-11, KU^q, qUq^qKqqqU, UKq^U qUq^qKqqqU ^KqqU^UKU^Uq qUq^qKqqqU
1.9912929E-11, PUt, PUtPUtPUPUt, PU PUtPUtPUPUt PUtPUtPUPUt PtPU
1.9912929E-11, PUt, UtPUtPUPUtP, PUP UtPUtPUPUtP UtPUtPUPUtP tPU
2.0273689E-11, OU^q, qOUq^qqOqq, UOq^U qOUq^qqOqq U^qqUO^UUO^Uq qOUq^qqOqq U
2.0332428E-11, EHI, HIEHIIEEHIE, HIEHIIEEHIE HI HIEHIIEEHIE IEHI
2.0907517E-11, UWjk, UkWUkUkWUkW, UkWUkUkWUkW j UkWUkUkWUkW UWWWUk
2.0907517E-11, UWk, UkWUkUkWUkW, UkWUkUkWUkW UkWUkUkWUkW UWWWUk
2.0907517E-11, UWk, kWUkUkWUkWU, U kWUkUkWUkWU kWUkUkWUkWU WWWUk
9.369183E-11, %PUk, PUkPU%kPUk, %PU%k PUkPU%kPUk PUkPU%kPUk PU%%k%%P%U%P%PUk
9.369183E-11, %PUk, UkPU%kPUkP, %PU%kP UkPU%kPUkP UkPU%kPUkP U%%k%%P%U%P%PUk
9.369183E-11, %PUk, kPU%kPUkPU, %PU%kPU kPU%kPUkPU kPU%kPUkPU %%k%%P%U%P%PUk
9.369183E-11, %PUk, kPUkPU%kPU, %PU% kPUkPU%kPU kPUkPU%kPU kPU%%k%%P%U%P%PUk
9.369183E-11, PU_k, PUkPUkPUkP, PUkPUkPUkP UkPUk_ PUkPUkPUkP _U_____P_PUk
9.369183E-11, PUjk, PUkPUkPUkP, PUkPUkPUkP UkPjUk PUkPUkPUkP UPPUk
9.369183E-11, PUk, PUkPUkPUkP, PUkPUkPUkP Uk PUkPUkPUkP UkPUPPUk
9.389669E-11, 9NPk, 9NPk9PNk9P, 9Pk9PkN9Pk 9NPk9PNk9P Nk 9NPk9PNk9P 9999PP9k
9.934108E-11, U^jq, qUq^qqqqU, Uq^U qUq^qqqqU ^qqjU^UU^Uq qUq^qqqqU
9.934108E-11, U^q, qUq^qqqqU, Uq^U qUq^qqqqU ^qqU^UU^Uq qUq^qqqqU
1.0306102E-10, #PUk, PUkPUk#PUk, PUkPUk#PUk #P#Uk#PUk PUkPUk#PUk P##U###PPUk
1.0306102E-10, PUjk, UkPUkPUkPU, P UkPUkPUkPU kPj UkPUkPUkPU kPUPPUk
1.0306102E-10, PUk, UkPUkPUkPU, P UkPUkPUkPU kP UkPUkPUkPU kPUPPUk
1.0348029E-10, @jq, qq@qqq@qq, @q qq@qqq@qq qj@ qq@qqq@qq
1.0348029E-10, @q, qq@qqq@qq, @q qq@qqq@qq q@ qq@qqq@qq
1.06478854E-10, 9PUp, PUp9PU9PUp, 9 PUp9PU9PUp 9PUp9 PUp9PU9PUp 9PU9Pp99U99PP9U
1.086519E-10, !9Pp, 9Pp9P!9Pp9, 9Pp9P!9Pp9 Pp! 9Pp9P!9Pp9 P9Pp999!9!PP9
1.086519E-10, 9KPp, 9Pp9PK9Pp9, 9Pp9PK9Pp9 KP
1.4901161E-8, 5jq, 5qqq5qq, qq 5qqq5qq qq5j555qq 5qqq5qq
1.4901161E-8, 5jq, q5qqq5q, q q5qqq5q qqq5j555q q5qqq5q q
1.4901161E-8, 5jq, qq5qqq5, qq5qqq5 qqqq5j555 qq5qqq5 qq
1.4901161E-8, 5q, 5qqq5qq, qq 5qqq5qq qq5555qq 5qqq5qq
1.4901161E-8, 5q, q5qqq5q, q q5qqq5q qqq5555q q5qqq5q q
1.4901161E-8, 5q, qq5qqq5, qq5qqq5 qqqq5555 qq5qqq5 qq
1.4901161E-8, 6Hjq, qqqHq6q, 6H qqqHq6q qqHqqj6H6HH6q qqqHq6q 66qH
1.4901161E-8, 6Hq, qqqHq6q, 6H qqqHq6q qqHqq6H6HH6q qqqHq6q 66qH
1.4901161E-8, 6Jq, 6qqqqq6, 6qJqqJq 6qqqqq6 6JJ 6qqqqq6 JqJ66q
1.4901161E-8, 6q, 6qqqqq6, 6qqqq 6qqqqq6 6 6qqqqq6 q66q
1.4901161E-8, Hjq, HqqqqHq, Hqqq HqqqqHq qjHH HqqqqHq qqH
1.4901161E-8, Hq, HqqqqHq, Hqqq HqqqqHq qHH HqqqqHq qqH
1.4901161E-8, Zjq, ZqqqqZq, Zqqq ZqqqqZq qjZZ ZqqqqZq Zqq
1.4901161E-8, Zq, ZqqqqZq, Zqqq ZqqqqZq qZZ ZqqqqZq Zqq
1.4901161E-8, fjqz, qqqzqqq, qqf qqqzqqq qjzfzfq qqqzqqq
1.4901161E-8, fqz, qqqzqqq, qqf qqqzqqq qzfzfq qqqzqqq
1.4901161E-8, jqz, qqqqzqq, q qqqqzqq qqjzz qqqqzqq q
1.4901161E-8, jqz, qqqzqqq, qq qqqzqqq qjzzq qqqzqqq
1.4901161E-8, qz, qqqqzqq, q qqqqzqq qqzz qqqqzqq q
1.4901161E-8, qz, qqqzqqq, qq qqqzqqq qzzq qqqzqqq
1.494586E-8, )BI, BBI)BI), BBI)BI) IB BBI)BI) I)I)BI)BBBIBI)I
1.494586E-8, 5BI, BBI5BI5, BBI5BI5 IB BBI5BI5 I5I5BIBB5B5IBII
1.494586E-8, BHI, BBHIBHI, BBHIBHI IB BBHIBHI HIHIBIBBHBIBIHI
1.5070409E-8, /Zep, /Zpe/ZpeZ, /Z/pee /Zpe/ZpeZ pe /Zpe/ZpeZ eeeZ
That is a very small sample. My output file has 5,000,000 lines in it! Also, many of those matches seem spurious. But, what is a good way to extract the non-spurious ones?
@smokie,
I wanted to do a part 2 in-depth cycle analysis of the smokie8 but I just can’t find anything. If you still want to see the cycles let me know. The following list are the discrepancies that may be of some worth. The numbers are with a new calculation.
Full: 155
Even rows mirrored: 156
Even columns only: 106
Uneven columns only: 140
So you may tell what you did (I give up). At least I was able to find out what plaintext you used. That made my day, but not today. ![]()
That is a very small sample. My output file has 5,000,000 lines in it! Also, many of those matches seem spurious. But, what is a good way to extract the non-spurious ones?
Thanks. Perhaps we should ask the question, can we determine the cause of randomization in the cycles of the 340? Either regular randomization/transposition or use of more than one key, is it possible to differentiate between the two?
One idea I have which requires quite a bit of work is to generate cycle n-grams.
– Compile from a large corpus lots of 63 symbol ciphers with 340 like distributions. One set with 2 keys and another with regular randomization.
– Compile 2 sets of cycle n-grams from these, from 2 to 6-grams or so.
– Score cycles in 340 or test ciphers with cycle n-grams.
Do you have any ideas?
As to your original question. Maybe using n-gram frequencies of unique sub-strings may work.
I believe the test ciphers are the way to go, since you can simulate all the interesting steps you think may have gone into the cipher construction.
My own work along these lines is making progress, but it very slow going. At the moment I am using a multiobjective hillclimber to generate ciphers that target many qualities of the real Z340 (I’ve even recently included the oddity of bigram distribution when all odd- and even-numbered positions are removed).
Once I’m happy with the resulting generated ciphers, I’ll rule out the conventional hypothesis ("Z340’s plaintext is written in the normal way, and enciphered using a method similar to Z408"). Then I plan to investigate Dan Olson’s hypothesis. Then if I have time I’ll look at some of the other ideas (wildcard symbols, multiple keys, transposition, etc). The difficulty is that once a new scheme is selected, I have to write new code to make adjustments to the encipherment process I use to extract candidate plaintexts from a large corpus. The scheme greatly affects the constraints imposed by the many features I’m looking for in the generated ciphers (pivots, box corners, even/odd discrepancy, filler, spelling errors, transcription errors, trigram that repeats in the same column, prime phobia of top two symbols, etc).
You were able to solve smokie8?
It is a two key cipher, alternating odds and evens. However, with smokie6 and smokie7, you were able to determine how many keys I used because cycle scores spiked as soon as you broke down the message into alternating parts. I encoded by hand, and started with the plaintext and an empty grid. I planted cross – key cycles of the same letter first. For example, E is a 1 on Key 1, and a 60 on Key 2. That’s the highest scoring two symbol cycle but it is mostly all odd – even alternating. I did that with several letters to try to make the message look like it was a one key and not a two key message. Some of the cycles that I made in step 1 were, however, disrupted by step two, where I encoded the remaining empty boxes in my grid. All of the cross – key cycles are true. If I could do it again, I would have made more of the cross – key symbols unique to the parts so that you would find them easier.
Zodiac didn’t do that. I have checked, and there are few if no high scoring cycles that alternate odd – even. But, after the exercise, I realized that Zodiac could have made the message appear to be more cyclic than it really is. He could have planted false cycles with alternating letters. However, I want to emphasize that this took some time, and effort. I do not see any practical reason for it when just using one key with some letters sharing the same symbols, or two alternating keys, makes the message so difficult. On the other hand, if I had not done that, then the score for the whole would have been in the EDIT: low 50,000s.
I did a little research into naturally occurring cycles in the alphabet, and guess what? There are some. G and H cycle together. That makes sense because of words like "thoughtful," etc. One idea I was thinking about is maybe making a statistical table of 26 * 25 naturally occurring letter cycles. High frequency letters cycle with each other to some degree. Take many random 340 letter sample from a corpus and compile cycle stats. I don’t know if it would help solve the 340, but since many of the cycles in that message are false… could statistics be used to determine if 1 3 1 3 1 3 1 3 is possible T and E are alternating with each other? Make a message with I like killing and only 26 symbols. You’ll find some high scoring cycles!
I will post smokie8 info soon. I am also working on comparing m7p77 with r3_p4_p3. We know that r3_p4_p3 has only one key but is randomized 30%. So I wanted to compare the 340 with m7p77 and r3_p4_s3 together, broken down into odds and evens to see if I can spot differences. Oh I also made a new spreadsheet that makes messages read backwards, snakewise, and up – down like Chinese. m7p77 appears to be encoded left to right, top to bottom.
I will be back soon.
EDIT:
Here is smokie8, where I planted a few cross – odd – even cycles to increase the cycle score for the whole message ( 1 and 60; 18 and 44 and a few other low scoring). The cycles in the keys are at most only repeated once or twice; then they are mostly random. The cycles for the high frequency letters are not perfect. Most of the high scoring cycles for the whole message, however, are FALSE.
1 60 8192 TRUE 1 60 1 60 1 60 1 60 1 60 1 60 1 60 0 0 0 0 0 0 0
4 18 4096 FALSE 18 18 4 18 4 18 4 18 4 18 4 18 4 18 18 0 0 0 0 0 0
38 60 4096 FALSE 60 38 60 38 60 38 60 38 60 38 60 38 60 0 0 0 0 0 0 0 0
22 46 2052 FALSE 46 22 22 46 46 46 22 46 22 46 22 46 22 46 22 46 22 0 0 0 0
9 46 1026 FALSE 46 46 9 46 9 46 9 46 9 46 9 46 46 46 9 9 0 0 0 0 0
16 48 1026 TRUE 48 16 16 48 16 48 16 48 16 48 16 48 16 16 0 0 0 0 0 0 0
15 56 528 FALSE 56 15 56 15 15 15 15 15 56 15 56 56 15 56 15 56 15 56 15 56 15
1 18 520 FALSE 1 18 1 18 1 18 1 18 1 18 18 1 18 18 1 18 0 0 0 0 0
34 48 516 FALSE 48 34 48 34 48 34 48 34 48 34 34 34 34 48 34 34 0 0 0 0 0
18 44 516 TRUE 44 18 44 44 18 44 18 44 18 44 18 44 44 18 44 18 44 18 44 18 44
4 38 514 FALSE 38 4 38 4 38 4 38 4 38 4 4 38 0 0 0 0 0 0 0 0 0
4 10 514 TRUE (odds) 10 10 10 4 10 4 10 4 10 4 10 4 4 10 10 0 0 0 0 0 0
1 48 514 FALSE 1 48 48 1 48 1 48 1 48 1 48 1 1 0 0 0 0 0 0 0 0
10 18 276 FALSE 10 18 10 18 10 10 18 18 10 18 10 18 10 18 10 18 18 10 0 0 0
32 50 268 FALSE 50 50 32 50 32 32 50 32 50 32 50 32 50 32 32 50 50 32 0 0 0
18 49 268 TRUE 18 49 18 49 18 49 18 49 18 18 49 18 18 49 18 49 0 0 0 0 0
15 16 266 TRUE (even) 16 16 15 15 15 16 15 15 16 15 15 16 15 16 15 16 15 16 15 15 0
1 44 266 FALSE 1 44 44 44 1 44 1 44 1 44 1 44 44 1 44 44 44 1 44 0 0
16 32 264 FALSE 32 16 16 32 32 16 16 32 32 16 32 16 32 16 32 16 32 0 0 0 0
9 15 264 FALSE 15 15 15 9 9 15 15 9 15 15 9 15 9 15 9 15 9 15 15 0 0
49 55 264 FALSE 55 55 49 49 55 55 55 49 55 49 55 49 55 49 55 55 49 55 0 0 0
10 38 262 FALSE 10 38 10 10 38 10 38 10 38 10 38 10 10 10 38 0 0 0 0 0 0
16 60 262 FALSE 16 60 16 16 16 60 60 16 60 16 60 16 60 16 60 0 0 0 0 0 0
50 52 256 TRUE 50 50 52 50 52 50 52 50 52 50 50 50 50 0 0 0 0 0 0 0 0
33 62 256 FALSE 33 62 33 62 33 62 33 62 33 0 0 0 0 0 0 0 0 0 0 0 0
The overall stats match up with the 340 very closely, but the 340 has 34 total cycles that score 256 or higher. Smokie8 has only 25!
Most of the high scoring cycles for the parts are FALSE:
15 44 132 FALSE odds 15 44 15 44 15 15 44 0 0 0 0 0 0 0 0 0
22 46 128 FALSE odds 22 46 46 22 46 22 46 46 0 0 0 0 0 0 0 0
8 9 128 TRUE odds 8 9 8 9 9 0 0 0 0 0 0 0 0 0 0 0
46 49 128 TRUE odds 46 46 46 46 49 46 0 0 0 0 0 0 0 0 0 0
1 46 256 FALSE odds 46 46 46 46 46 1 1 0 0 0 0 0 0 0 0 0
4 22 130 FALSE odds 22 22 22 4 0 0 0 0 0 0 0 0 0 0 0 0
55 56 4098 TRUE even 55 56 55 56 55 56 55 56 55 56 55 56 55 55 56 56
32 46 258 FALSE even 46 32 32 46 32 46 32 46 32 46 32 32 32 0 0 0
34 38 256 FALSE even 34 34 38 34 38 34 38 34 38 34 0 0 0 0 0 0
38 60 256 FALSE even 60 60 38 60 38 60 38 60 38 60 0 0 0 0 0 0
34 60 136 FALSE even 34 60 34 60 60 34 60 34 60 34 60 34 0 0 0 0
34 48 132 FALSE even 48 34 48 34 48 34 48 34 34 48 34 0 0 0 0 0
32 60 132 FALSE even 60 32 32 32 60 60 32 60 32 60 32 60 32 32 0 0
18 48 130 FALSE even 18 48 48 18 48 18 48 18 48 18 18 18 0 0 0 0
15 46 128 FALSE even 15 46 15 46 15 46 15 46 46 0 0 0 0 0 0 0
Key 1 for the odds:
A 10 3 4
B 5
C 6 7
D 8 9
E 1 11 12 13 15
F 16
G 17
H 18 19 20 21
I 22 23 25 26
J
K 27
L 28 29 30
M 31
N 32 33 34 35
O 36 37 39 40
P 41 42
Q
R 43 44 45
S 46 47 48 49
T 50 51 52 53 54
U 55 56
V 57
W 58 59
X 61
Y 62
Z 63
Key 2 for the evens:
A 49 61 62 63
B 59
C 57 58
D 55 56
E 60 50 51 52 54
F 48
G 47
H 44 45 46
I 38 39 40 41
J
K 37
L 34 36
M 33
N 29 30 32
O 24 26 27 28
P 22 23
Q
R 19 20 21
S 15 16 18
T 10 12 13 14
U 8 9
V 7
W 5 6
X 4
Y 3
Z 2
Here is the message:
50 45 43 50 1 57 36 33 41 61 44 10 31 51 32 12 46
55 23 7 25 56 11 55 51 18 12 58 24 48 16 52 45 34
29 13 20 60 16 39 44 15 50 59 28 62 63 54 8 22 22
36 13 46 37 48 17 36 26 56 15 32 6 26 38 30 23 32
52 44 1 15 11 57 39 29 9 5 12 19 13 20 10 30 17
50 8 59 49 43 47 27 16 8 33 23 24 34 25 46 21 51
9 47 36 36 8 6 18 40 7 44 42 24 48 15 15 16 46
52 9 32 40 14 20 22 29 47 3 12 10 21 4 58 53 41
57 60 49 63 57 54 50 46 1 38 45 7 10 36 55 60 22
32 54 18 12 14 19 41 19 2 15 55 31 36 34 56 17 43
3 15 41 52 8 45 4 29 9 48 56 36 46 24 16 55 26
61 31 36 35 56 15 22 11 63 19 34 49 62 33 55 44 9
5 38 1 18 58 46 22 58 44 49 46 10 21 60 62 48 1
34 29 28 33 26 34 50 4 32 24 50 18 51 44 16 40 8
34 56 13 55 30 38 27 60 44 62 22 34 10 47 4 38 35
18 10 47 29 63 15 46 49 48 51 1 44 45 4 7 26 32
17 13 36 9 6 18 13 56 16 60 23 13 11 4 10 33 22
32 12 55 53 44 13 18 15 50 44 1 49 18 55 43 11 16
12 55 31 24 34 56 45 9 49 45 15 56 51 45 44 27 55
47 20 13 21 54 6 10 57 50 19 32 15 34 38 37 60 61
And here is the plaintext:
T h r e e c o m p a r t m e n t s
d i v i d e d t h e c o f f e r I
n t h e f i r s t b l a z e d p i
l e s o f g o l d e n c o i n i n
t h e s e c o n d w e r e r a n g
e d b a r s o f u n p o l i s h e
d g o l d w h i c h p o s s e s s
e d n o t h i n g a t t r a c t i
v e s a v e t h e i r v a l u e i
n t h e t h i r d E d m o n d g r
a s p e d h a n d f u l s o f d i
a m o n d s p e a r l s a n d r u
b i e s w h i c h a s t h e y f e
l l o n o n e a n o t h e r s o u
n d e d l i k e h a i l a g a i n
s t g l a s s A f t e r h a v i n
g t o u c h e d f e l t e x a m i
n e d t h e s e t r e a s u r e s
E d m o n d r u s h e d t h r o u
g h t h e c a v e r n s l i k e a
It is a quote from Count of Monte Cristo.
There are 41 bigram repeats, many of which are not actual repeats because of the two keys.
I believe the test ciphers are the way to go, since you can simulate all the interesting steps you think may have gone into the cipher construction.
My own work along these lines is making progress, but it very slow going. At the moment I am using a multiobjective hillclimber to generate ciphers that target many qualities of the real Z340 (I’ve even recently included the oddity of bigram distribution when all odd- and even-numbered positions are removed).
Once I’m happy with the resulting generated ciphers, I’ll rule out the conventional hypothesis ("Z340’s plaintext is written in the normal way, and enciphered using a method similar to Z408"). Then I plan to investigate Dan Olson’s hypothesis. Then if I have time I’ll look at some of the other ideas (wildcard symbols, multiple keys, transposition, etc). The difficulty is that once a new scheme is selected, I have to write new code to make adjustments to the encipherment process I use to extract candidate plaintexts from a large corpus. The scheme greatly affects the constraints imposed by the many features I’m looking for in the generated ciphers (pivots, box corners, even/odd discrepancy, filler, spelling errors, transcription errors, trigram that repeats in the same column, prime phobia of top two symbols, etc).
Thanks again for the help with MUJ and the odd – even phenomenon. I appreciate your time!
Here is more info about m7p77:
I believe that it is a two key cipher because the scores seem a bit high there. It is amazing how the 340 is so even, but with other two part ciphers, the scores are high and low.
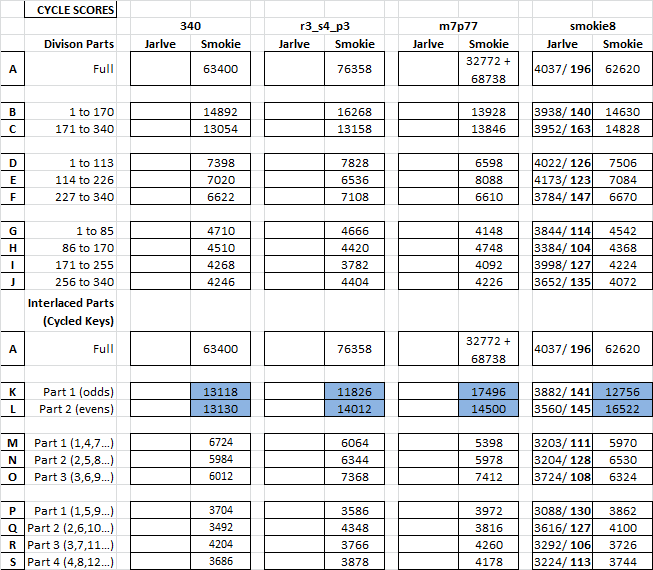
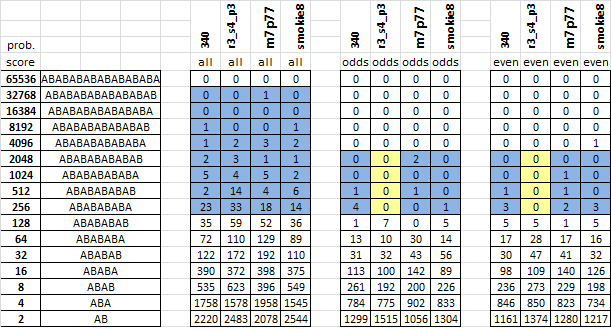
However, this is a comparison of cycle score details with 340, r3_s4_p3, which we know has only one key, m7p77, and smokie8, which we think and know have two keys. The only message that does not contain cycles above 256 in the odds and evens is r3_s4_p3.
However, if you drop down to the 128 score line, all of the messages seem to line up quite well. My threshold so far is 256, but I need to do some more randomization research to learn more about how to analyze odds and evens scores.
I think that m7p77 is closer to the 340 than any other message so far, and have a couple more things to do with it.
EDIT: Here is a table with Part 1 and Part 2 cycle scores compared to the average of ten randomizations of Part 1 and Part 2 cycle scores:
r3_s4_p3 is a one key message, but the numbers are comparable to the 340. m7p77 seems to be a two key message. Smokie8 is very different.
So this approach has not helped me to figure out what the 340 is (as usual). But my final conclusion about m7p77 is that it is a two key message.