I see what’s going on, if you check the last line of doranchak’s alteration:

H^LEVTRPG>k2p|dl1

Skip 2 symbols and wrap around the row if needed. I haven’t checked if it’s consistent for the whole cipher but if it is then it’s interesting to know that the bigram 19 thing could also relate to columnar transposition or variations of it.

EDIT: each row has a different transposition, in effect causing a randomization of the rows, so the information stays on the same row preserving the bulk of the encoding information. I tested the 408 randomizing each row and the cycle score was still much higher than with the 340. Speculating that transposition/randomization of symbols per row alone is not enough to cause the 340 to be less cyclic than the 408.

Here are five versions of the 340 with horizontal – vertical un-transposition.

340_323_17 means that the original message was 17×19 and there are 17 gibberish symbols at the end.

340_324_16 means that the original message was 17×20 and there are 16 gibberish symbols at the end.

I only went to 340_327_13 because at that point, a couple of high scoring period 18/19 bigrams that should have been reconstructed to period 0/1 bigrams were destroyed.

They all have more bigram repeats in the second half.

I will highlight the gibberish for clarity.

340_323_17
1 19 37 44 11 56 8 60 31 19 6 33 16 2 28 20 33
2 20 19 30 50 10 28 13 55 3 3 19 53 4 32 11 5
3 21 38 8 51 51 40 47 40 54 41 18 61 8 37 33 11
4 22 39 45 9 4 13 17 6 50 11 11 28 38 57 13 51
5 23 15 5 19 16 11 29 38 48 30 50 36 39 15 19 10
6 24 26 23 52 25 21 37 8 2 53 51 8 50 16 19 17
7 25 21 19 53 21 15 19 19 11 14 20 53 55 3 33 26
8 26 33 19 10 22 16 61 7 25 50 36 48 19 36 26 29
9 27 13 3 54 50 41 19 41 27 37 21 19 11 14 56 43
10 28 22 31 5 19 32 39 19 20 28 58 19 36 19 40 48
11 29 40 16 44 31 49 3 23 5 19 44 34 28 13 26 20
12 30 1 46 3 57 22 16 5 61 52 3 20 45 12 36 46
13 31 41 47 7 24 23 51 43 14 20 6 59 40 16 9 27
14 32 42 37 51 58 19 20 29 37 51 15 12 20 56 23 23
15 33 5 19 6 16 46 36 51 31 40 51 30 31 29 42 20
16 20 5 40 23 38 18 34 20 23 63 18 35 21 19 1 30
17 34 43 48 55 36 27 62 34 16 47 7 53 23 51 14 55
18 35 7 49 30 59 40 63 55 29 42 32 47 5 6 54 56
5 36 6 17 17 15 19 53 38 36 34 50 56 7 26 21 36
4 37 25 1 18 5 10 42 40 39 23 44 62 11 31 58 19

340_324_16
1 20 19 30 50 10 28 13 55 3 3 19 53 4 32 11 5
2 21 38 8 51 51 40 47 40 54 41 18 61 8 37 33 11
3 22 39 45 9 4 13 17 6 50 11 11 28 38 57 13 51
4 23 15 5 19 16 11 29 38 48 30 50 36 39 15 19 10
5 24 26 23 52 25 21 37 8 2 53 51 8 50 16 19 17
6 25 21 19 53 21 15 19 19 11 14 20 53 55 3 33 26
7 26 33 19 10 22 16 61 7 25 50 36 48 19 36 26 29
8 27 13 3 54 50 41 19 41 27 37 21 19 11 14 56 43
9 28 22 31 5 19 32 39 19 20 28 58 19 36 19 40 48
10 29 40 16 44 31 49 3 23 5 19 44 34 28 13 26 20
11 30 1 46 3 57 22 16 5 61 52 3 20 45 12 36 46
12 31 41 47 7 24 23 51 43 14 20 6 59 40 16 9 27
13 32 42 37 51 58 19 20 29 37 51 15 12 20 56 23 23
14 33 5 19 6 16 46 36 51 31 40 51 30 31 29 42 20
15 20 5 40 23 38 18 34 20 23 63 18 35 21 19 1 30
16 34 43 48 55 36 27 62 34 16 47 7 53 23 51 14 55
17 35 7 49 30 59 40 63 55 29 42 32 47 5 6 54 56
18 36 6 17 17 15 19 53 38 36 34 50 56 7 26 21 36
5 37 44 11 56 8 60 31 19 6 33 16 2 28 20 33 4
19 37 25 1 18 5 10 42 40 39 23 44 62 11 31 58 19

340_325_15
1 20 38 8 51 51 40 47 40 54 41 18 61 8 37 33 11
2 21 39 45 9 4 13 17 6 50 11 11 28 38 57 13 51
3 22 15 5 19 16 11 29 38 48 30 50 36 39 15 19 10
4 23 26 23 52 25 21 37 8 2 53 51 8 50 16 19 17
5 24 21 19 53 21 15 19 19 11 14 20 53 55 3 33 26
6 25 33 19 10 22 16 61 7 25 50 36 48 19 36 26 29
7 26 13 3 54 50 41 19 41 27 37 21 19 11 14 56 43
8 27 22 31 5 19 32 39 19 20 28 58 19 36 19 40 48
9 28 40 16 44 31 49 3 23 5 19 44 34 28 13 26 20
10 29 1 46 3 57 22 16 5 61 52 3 20 45 12 36 46
11 30 41 47 7 24 23 51 43 14 20 6 59 40 16 9 27
12 31 42 37 51 58 19 20 29 37 51 15 12 20 56 23 23
13 32 5 19 6 16 46 36 51 31 40 51 30 31 29 42 20
14 33 5 40 23 38 18 34 20 23 63 18 35 21 19 1 30
15 20 43 48 55 36 27 62 34 16 47 7 53 23 51 14 55
16 34 7 49 30 59 40 63 55 29 42 32 47 5 6 54 56
17 35 6 17 17 15 19 53 38 36 34 50 56 7 26 21 36
18 36 44 11 56 8 60 31 19 6 33 16 2 28 20 33 4
5 37 30 50 10 28 13 55 3 3 19 53 4 32 11 5 37
19 19 25 1 18 5 10 42 40 39 23 44 62 11 31 58 19

340_326_14
1 20 38 45 9 4 13 17 6 50 11 11 28 38 57 13 51
2 21 39 5 19 16 11 29 38 48 30 50 36 39 15 19 10
3 22 15 23 52 25 21 37 8 2 53 51 8 50 16 19 17
4 23 26 19 53 21 15 19 19 11 14 20 53 55 3 33 26
5 24 21 19 10 22 16 61 7 25 50 36 48 19 36 26 29
6 25 33 3 54 50 41 19 41 27 37 21 19 11 14 56 43
7 26 13 31 5 19 32 39 19 20 28 58 19 36 19 40 48
8 27 22 16 44 31 49 3 23 5 19 44 34 28 13 26 20
9 28 40 46 3 57 22 16 5 61 52 3 20 45 12 36 46
10 29 1 47 7 24 23 51 43 14 20 6 59 40 16 9 27
11 30 41 37 51 58 19 20 29 37 51 15 12 20 56 23 23
12 31 42 19 6 16 46 36 51 31 40 51 30 31 29 42 20
13 32 5 40 23 38 18 34 20 23 63 18 35 21 19 1 30
14 33 5 48 55 36 27 62 34 16 47 7 53 23 51 14 55
15 20 43 49 30 59 40 63 55 29 42 32 47 5 6 54 56
16 34 7 17 17 15 19 53 38 36 34 50 56 7 26 21 36
17 35 6 11 56 8 60 31 19 6 33 16 2 28 20 33 4
18 36 44 50 10 28 13 55 3 3 19 53 4 32 11 5 37
5 37 30 51 51 40 47 40 54 41 18 61 8 37 33 11 25
19 19 8 1 18 5 10 42 40 39 23 44 62 11 31 58 19

340_327_13
1 20 38 45 19 16 11 29 38 48 30 50 36 39 15 19 10
2 21 39 5 52 25 21 37 8 2 53 51 8 50 16 19 17
3 22 15 23 53 21 15 19 19 11 14 20 53 55 3 33 26
4 23 26 19 10 22 16 61 7 25 50 36 48 19 36 26 29
5 24 21 19 54 50 41 19 41 27 37 21 19 11 14 56 43
6 25 33 3 5 19 32 39 19 20 28 58 19 36 19 40 48
7 26 13 31 44 31 49 3 23 5 19 44 34 28 13 26 20
8 27 22 16 3 57 22 16 5 61 52 3 20 45 12 36 46
9 28 40 46 7 24 23 51 43 14 20 6 59 40 16 9 27
10 29 1 47 51 58 19 20 29 37 51 15 12 20 56 23 23
11 30 41 37 6 16 46 36 51 31 40 51 30 31 29 42 20
12 31 42 19 23 38 18 34 20 23 63 18 35 21 19 1 30
13 32 5 40 55 36 27 62 34 16 47 7 53 23 51 14 55
14 33 5 48 30 59 40 63 55 29 42 32 47 5 6 54 56
15 20 43 49 17 15 19 53 38 36 34 50 56 7 26 21 36
16 34 7 17 56 8 60 31 19 6 33 16 2 28 20 33 4
17 35 6 11 10 28 13 55 3 3 19 53 4 32 11 5 37
18 36 44 50 51 40 47 40 54 41 18 61 8 37 33 11 25
5 37 30 51 4 13 17 6 50 11 11 28 38 57 13 51 1
19 19 8 9 18 5 10 42 40 39 23 44 62 11 31 58 19

Jarlve, thanks for updating the first post test cipher menu. I appreciate your work with that and keeping things organized.

I am still thinking about how Zodiac could have rearranged the plaintext to cause so many period bigram repeats. I like the smokie/daikon transposition hypothesis because it would have been in a cryptography book and so simple to use. It is one step of a columnar transposition cipher, but there is no re-arrangement of the columns. There is only the transposition.

I tried to solve them and it didn’t work. I also tried to use the z ngram files to see if it would flush out any polyalphabetic symbols, and ZKD usually found either symbols 19 or 20 to be the Z, but didn’t get any solves.

I am still thinking about transposition shuffling, and I have to look at doranchak’s scheme some more. Is there any other scheme that would cause a period bigram shift like that? I was also thinking that the smokie/daikon idea assumes that Zodiac skipped Row 20 when in fact he could have skipped any of the rows, like Row 1 or whatever. He could have cycled the rows that he skipped, or whatever.

@smokie, I added 3 alterations of the 340 based on the bigram period 19 repeats (check under alterations of the 340). I think doranchak’s original interpretation (based on the scheme of the 21 by 21 magic square?) is the most interesting because it also creates the most 3-grams.

And there’s something else going on with it, when applied any vertical transposition scheme to it the cycle scores approach that of the normal 340! Is this just a magic trick or is there more going on?

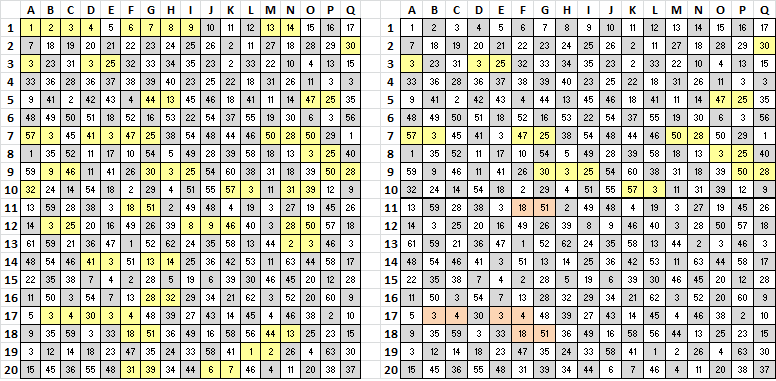
340_d1_n-e.txt

NO+p8>kAMS|DzKHZ;
kB-d_CWYc<O|7BFt*
+WT+c/)P(WO)CSpzH
)LFL1lR6WcCBT<|++
M.Oq3pGz^2B.|Kfc(
Vy4UB9ZXC51E-*>+:
b+^.+fcl5VG24F4tN
N(9|;S58yFR#Bz+c6
JM2|.<*+c5&lTBR4F
/YK5BOtpUEb+|TRDM
zJFl+BUOyVp-+7-^<
K+cdZy<RAM26+F4bB
@J_LfN9jY(#zGO+2+
V52.+UzKcLqX|%G#;
C(lkpOF8->R*2^dDF
|4+5kzF/tP_j+9d&M
8+p*+pVR73K^p2lOS
M(J+)BULyZ#:GzcWH
+DKBWf(Y)#.NO<p%*
H^LEVTRPG>k2p|dl1

1  2  3  4  5  6  7  8  9  10 11 12 13 14 15 16 17
7  18 19 20 21 22 23 24 25 26 2  11 27 18 28 29 30
3  23 31 3  25 32 33 34 35 23 2  33 22 10 4  13 15
33 36 28 36 37 38 39 40 23 25 22 18 31 26 11 3  3
9  41 2  42 43 4  44 13 45 46 18 41 11 14 47 25 35
48 49 50 51 18 52 16 53 22 54 37 55 19 30 6  3  56
57 3  45 41 3  47 25 38 54 48 44 46 50 28 50 29 1
1  35 52 11 17 10 54 5  49 28 39 58 18 13 3  25 40
59 9  46 11 41 26 30 3  25 54 60 38 31 18 39 50 28
32 24 14 54 18 2  29 4  51 55 57 3  11 31 39 12 9
13 59 28 38 3  18 51 2  49 48 4  19 3  27 19 45 26
14 3  25 20 16 49 26 39 8  9  46 40 3  28 50 57 18
61 59 21 36 47 1  52 62 24 35 58 13 44 2  3  46 3
48 54 46 41 3  51 13 14 25 36 42 53 11 63 44 58 17
22 35 38 7  4  2  28 5  19 6  39 30 46 45 20 12 28
11 50 3  54 7  13 28 32 29 34 21 62 3  52 20 60 9
5  3  4  30 3  4  48 39 27 43 14 45 4  46 38 2  10
9  35 59 3  33 18 51 36 49 16 58 56 44 13 25 23 15
3  12 14 18 23 47 35 24 33 58 41 1  2  26 4  63 30
15 45 36 55 48 31 39 34 44 6  7  46 4  11 20 38 37

Yes, my cycle scores:

1-340 = 68144
1-170 = 13184
171 – 340 = 15122

I think that the cycle scores improved because we are still working from left to right basically. I can switch two symbols and get that big of a difference. Does this suggest stepped transposition after encoding? I will have to take a closer look at the cycles.

Bigram repeats on the left, and by half on the right.

I am not quite clear how the transposition scheme for this one works, though.

I have been messing around with different configurations of mine and daikon’s idea. Just for a short while every night. I have been thinking about trying to figure it out. Some have two whole contiguous rows with no bigram repeats. I would like to try to find one that maximizes bigram repeats. With either system, it’s tough to figure out where he started or if he skipped anything. Maybe there is some evidence…

The prospect came through. I was saving one piece of wood until that happened, and painted it today. The summer of 2015 is officially over.

I am going to put this thing on the shelf for a while and think about it. I am just buried with other things right now, but putting down a note to myself for the future.

I would like to explore different plaintext transposition schemes that will cause period 18/19 bigram repeats. I want to update my spreadsheets so that I can rearrange the symbols in a proposed original order, and then score the period 0 bigram repeats, and maybe include the period 1 and period 2 bigram repeats as well. Try different schemes, and find the one(s) with the highest total scores. Compare with messages in the message library, and maybe make some test messages to find out how the system works. See if one particular plaintext transposition scheme for the 340 stands out above all others according to total bigram repeat score. Then maybe play around with that one, if there is such.

To be continued…

Well I have been doing some thinking about a lot of things. Here is a fun new message that is approximately close to what I think that he did.

smokie9:

11 3 8 5 21 13 36 34 55 17 18 23 1 34 53 33 27
19 59 44 43 12 1 48 11 7 34 53 30 6 40 38 57 19
36 9 14 37 57 1 28 4 26 32 16 19 7 31 18 49 41
55 19 46 52 39 63 7 19 43 50 20 19 9 20 58 42 33
14 55 53 34 59 61 6 29 27 20 39 9 62 5 48 20 52
23 2 1 46 42 25 7 61 49 11 19 58 55 33 18 3 19
10 27 43 19 4 29 30 56 57 34 60 53 20 12 26 62 42
20 19 3 52 48 20 13 30 45 21 9 18 14 23 49 52 37
5 39 5 16 58 8 33 30 1 36 26 14 11 34 56 51 41
19 9 12 37 60 19 20 43 62 2 52 36 55 47 19 19 42
57 16 19 57 39 5 30 18 41 11 61 19 3 53 20 49 9
17 53 9 58 42 48 61 8 15 43 44 60 9 11 34 35 25
22 54 63 62 55 31 34 42 55 62 24 52 58 34 43 53 4
19 56 9 5 1 34 36 30 20 21 55 49 52 27 47 7 34
23 1 22 19 32 10 3 13 53 33 48 39 34 12 7 38 7
1 50 53 20 26 37 43 9 30 44 35 62 56 16 54 17 57
30 57 19 58 49 48 8 39 39 55 2 6 13 38 19 19 14
5 34 45 53 19 18 34 40 34 28 20 53 30 33 1 53 42
32 43 22 11 49 62 34 41 29 20 52 19 36 13 1 12 5
27 30 28 48 63 61 49 25 14 21 23 53 55 19 19 60 47

I will give some hints.

The actual message is close to 323 plaintext long, +/- 4. To find out how many plaintext there are, compare the bigram lists for plus 18, plus 19, and plus 20. See which ones have the most shared, and then find whether more of the plus 18 or plus 20 that are in common with plus 19 gather to the beginning of the message. Also, find a way to score the plus whatever bigram repeats and sort them according to score.

There are also two high count symbols that do not cycle well overall with the other symbols. Ah, but do they not? They map to several plaintext each, making them high count, but also giving them lower overall total cycle scores. That is why they look like they could be 1:1 substitutes, but they are not.

Symbol selection when encoding the cycles is about 25% random.

Analyze and compare with the 340.

Then If you do everything right, you should at least be able to find a few long words…

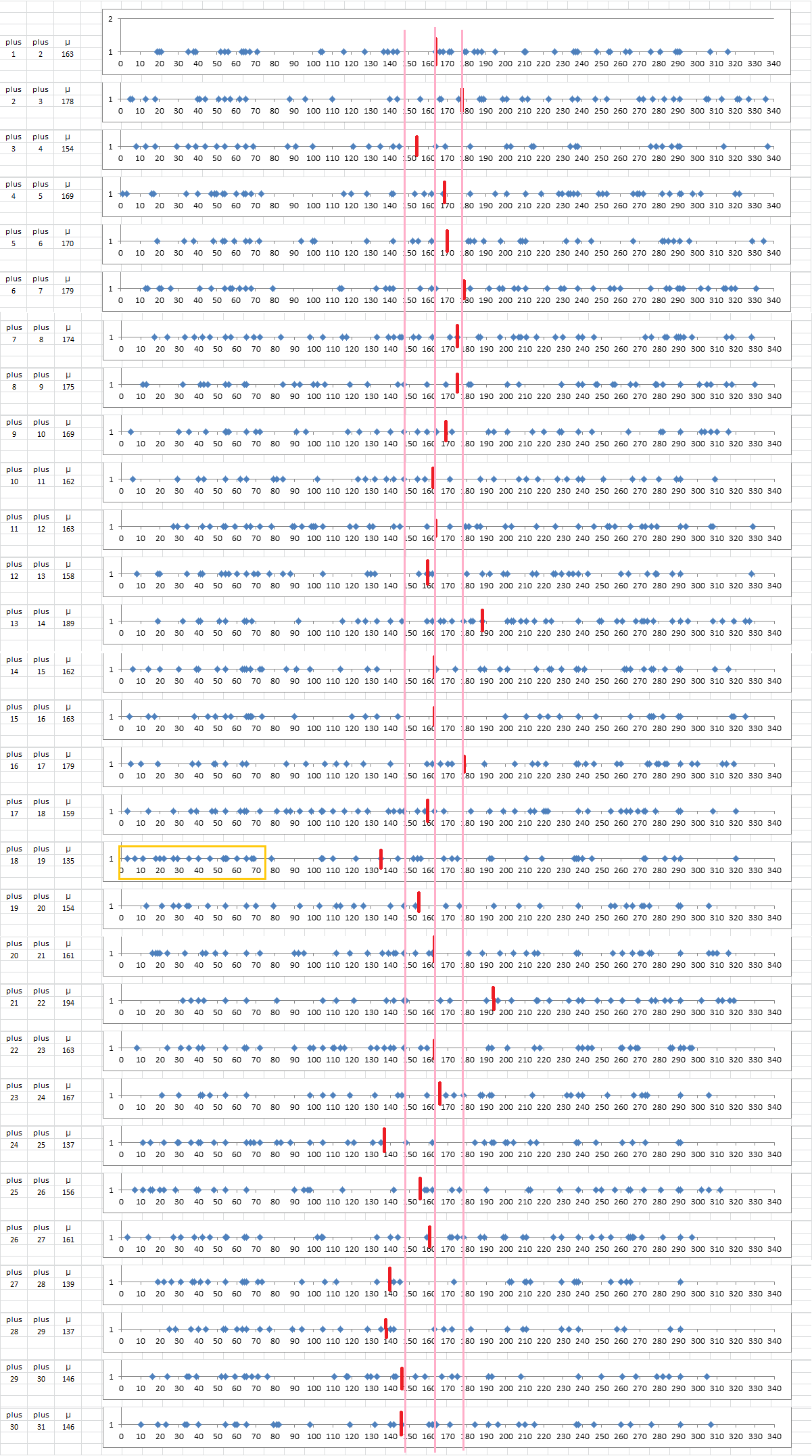
Anyway, so I compared the list of plus 1 and plus 2 bigraphs and found matches and plotted their positions on a little horizontal scatter graph. And I did that all the way up to plus 30 and 31 bigraphs. Then I compared all of them to each other.

The red marks are the mean for each scatter graph. The pink lines show the mean of the means, and the standard deviations of the means. I was looking in particular to see if there was an inordinate number of plus 18 and plus 19 matches, or perhaps plus 19 and plus 20 matches. The mean for the plus 18 and plus 19 matches is outside the standard deviation, and there is a clustering of plus 18 and plus 19 matches in the first 72 symbols of the message. That is the orange rectangle.

So this may not be extraordinary statistics, but may be evidence that the message is a few plaintext short of 323 and that he transposed vertically.

I have not yet checked other transpositions schemes. I have more information to post later regarding bigraph repeat scores and the symbols that are in high scoring plus 19 bigraph repeat scores.

EDIT: The x-axis is symbol position.

Sorry for perhaps asking about an obvious thing, but what do you mean by "plus 1/2/etc." bigraphs? I’d love to contribute to the discussion, but I seem to be missing understanding of an important detail. 🙂

Sorry about that, and I did intend to mention it. AB is a plus 1 bigraph, A_B is a plus 2 bigraph, etc. There seems to be some confusion about what to call them. Step, period and whether to count the relative position of B to A in an AB or not. I called them plus 1, plus 2, etc. because if A is at position 1 and B is at position 2, then the position of B is the position of A plus 1 (I use a spreadsheet).

You were talking about how knowing the message length would help when we simultaneously drafted the vertical transposition idea. I am wondering if the message is slightly under 323 symbols long, and if he transposed vertically from right to left instead of a message that is slightly over 323 symbols long and him transposing vertically from left to right. If you put the list of plus 18 bigraphs (not necessarily repeats) next to the list of plus 19 bigraphs (not necessarily repeats) and compare them, there are a lot of plus 18 bigraphs in the first few rows of the message that match up with plus 19 bigraphs in the remaining part of the message. Actually, they exist more prominently in the first +/- 72 symbols of the message. 18 * 4 = 72.

You were also talking about trying "snake" routes. I haven’t compared lists of bigraphs to see if there seem to be a high number of ABs that match up with BAs. It seems that "snake" would decrease the number of period 18 bigraph (or "plus 19") repeats.

Also, vertical transposition would explain the low number of "apparent" bigraph repeats in the second half. It is not difficult to re-create, since Ts won’t line up with Hs as often as they would in natural language,etc. I made a lot of messages and sometimes there were only one or two repeats in the top half. Check smokie9 a few posts above. I didn’t get the numbers exactly the same, but they are similar.

EDIT: Here is another one. I randomized the cyclic symbol selection when encoding about 25%. It took me only eight clicks on "calculate now" to get it. Check to see how many bigraph repeats there are in the first half versus the second half. It is the same plaintext , key and vertical transposition scheme as smokie9.

Smokie10:

55 3 8 30 21 20 36 9 55 20 18 23 1 34 53 33 2
19 15 44 19 37 26 1 11 32 9 9 30 6 40 38 38 62
36 53 14 37 20 1 28 4 48 32 16 19 51 31 18 49 41
55 19 46 52 14 63 7 19 62 6 13 19 9 13 58 20 8
14 11 34 34 59 61 6 29 27 61 58 53 62 5 48 17 30
23 2 1 46 42 25 32 61 49 36 19 58 55 33 18 3 33
35 27 43 52 4 29 19 56 57 34 60 53 20 56 26 62 17
20 19 28 19 48 60 13 30 22 21 34 18 14 23 49 52 37
19 39 5 16 58 8 8 30 1 19 26 39 36 34 56 51 41
19 53 12 37 60 19 20 43 19 2 52 36 55 47 19 30 42
38 16 18 57 39 49 5 43 41 11 61 36 28 9 20 49 34
17 53 9 58 42 48 61 8 15 19 44 20 34 55 53 35 25
45 54 63 43 19 50 9 20 19 62 24 52 14 34 43 53 29
5 56 9 19 1 34 36 30 20 21 55 49 49 27 47 7 53
46 26 22 19 32 54 28 57 9 33 48 39 53 12 51 38 7
1 50 53 20 26 37 43 9 5 44 35 62 56 16 54 42 57
30 20 19 58 49 48 8 14 39 55 2 6 57 38 52 19 58
5 53 45 53 19 18 9 40 34 3 57 53 30 33 1 34 20
32 43 22 11 49 19 34 41 29 20 52 19 36 13 26 12 49
27 30 28 48 63 61 49 25 14 21 23 53 55 19 19 60 47

Ah, I see, now it all makes sense.
I’ve tried cracking your smokie9 cipher, but I have to admit, I’m not getting a solve. There is a distinct spike in bigram repeats at period 19 (plus 19 in your terminology), which seems to suggest a transposition with the width 19. So I tried that and didn’t get a coherent solution. Then I tried reducing the length of the message one symbol at a time down to 318 (you are hinting at 323 symbols +/- 4, so I went 1 symbol beyond, just to be sure :). No stable solves. Then I tried the same, but reading the cipher in reverse (backwards). Nothing. Is it not a straight transposition? Did you do some else there?

The smokie10 cipher has a bigram repeats spike at period 12, so I’m running transpositions of width 12 and of different lengths (down to 318), and then in reverse, through my solver. Will let you know if I get something…

K, so here is the proposed 340 cipher:

1. Zodiac drafted his message normally, from left to right, top to bottom, and with 17 columns. The message was a few plaintext short of 323 and just under 19 rows.

2. Zodiac re-drafted the message, working from the rightmost column to the leftmost column, transposing either up or down.

3. Zodiac encoded the transposed plaintext with cycles. He selected the symbols in cycle sequence, but randomized symbol selection about 25%-30%. Alternatively, he used two keys. One for odds and one for evens, which makes the symbol selection appear to be about 25% to 30%.

4. The key was relatively flat, meaning that there was not a great deal of variation between the symbol counts mapping to the different plaintext.

5. There were a few symbols that mapped to more than one plaintext, making them polyalphabetic and also causing their respective cycle statistics to make them appear to be 1:1 substitutes.

6. Zodiac filled in the last 17+ symbols as gibberish.

I am a little burned out tonight after a hectic week. But will show more of my work soon, starting with how I can easily re-create the low bigraph repeat count in one of the two halves of the message using vertical transposition.

Good night.

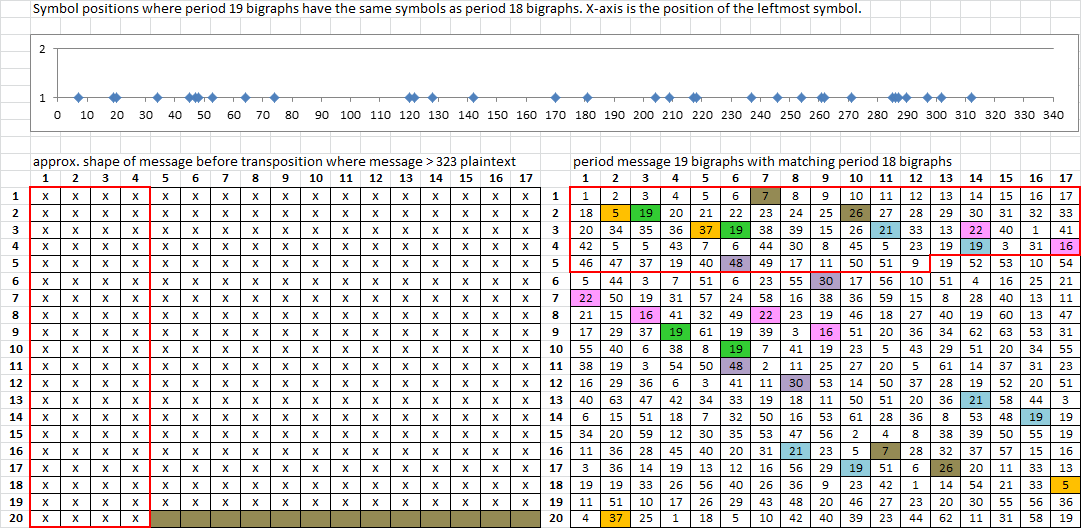
EDIT: Daikon, smokie9 mimics what I think the 340 approximately is. Thanks for working on it. Compare the lists of period 17 (plus 18) and period 18 (plus 19) bigraphs. Not necessarily the repeats. Just all 339 of each. Find where in the message that they are most in common. A message that is 319 symbols long, for instance, and transposed vertically from rightmost column to leftmost column, should have a lot of period 17 (plus 18) bigraphs in the first few rows of the message that have symbols matching up with period 18 (plus 19) bigraphs in the remainder of the message. If the message was what we originally guessed, a few plaintext longer than 17 rows and transposed vertically from left to EDIT: right, there would be more period 19 (plus 20) bigraphs in the first few rows with symbols that match up with period 18 (plus 19) bigraphs in the remainder of the message. The whole idea is to try to figure out how long the true message really is.

EDIT: This might help.

Daikon, smokie9 mimics what I think the 340 approximately is. Thanks for working on it.

Finished the smokie10 transpositions of width 12 of different lengths, didn’t get a stable solve. There must be something else going there. Are you hinting that you used 2 separate keys for odds/evens in smokie9 and smokie10?

Compare the lists of period 17 (plus 18) and period 18 (plus 19) bigraphs. Not necessarily the repeats. Just all 339 of each. Find where in the message that they are most in common. A message that is 319 symbols long, for instance, and transposed vertically from rightmost column to leftmost column, should have a lot of period 17 (plus 18) bigraphs in the first few rows of the message that have symbols matching up with period 18 (plus 19) bigraphs in the remainder of the message. If the message was what we originally guessed, a few plaintext longer than 17 rows and transposed vertically from left to left, there would be more period 19 (plus 20) bigraphs in the first few rows with symbols that match up with period 18 (plus 19) bigraphs in the remainder of the message. The whole idea is to try to figure out how long the true message really is.

Sorry, you completely lost me there. 🙂 I’m not sure how comparing bigrams at different periods helps establish the length of the message?

Daikon, look at the new picture of the 340 that I posted in my edit above. You will get it.

I get it now (hopefully). I think smokie is asking us to reconsider the wildcard hypothesis factoring in the period 19 bigram peak (in the form of vertical transposition, excluding some part of the cipher). So the reason why we are not solving smokie9 and 10 (and possibly the 340) is because of the wildcards, which we’ll have to expand first.

smokie9 will solve easily without expanding the polyalphabetic symbols. There are only two and total count isn’t high enough to make the message unsolve-able. However, I would suggest not trying to solve the last row plus or minus a few symbols.

You just have to un-transpose it right, and I didn’t do anything particularly crazy. It is very straightforward.

It’s not the wildcard hypothesis, which said that Zodiac used the + and B and a few other symbols to either disrupt the cycles or mask the bigram repeats. But it is a similar polyalphabetic explanation for the distribution of symbol counts and fact that three or four symbols do not cycle well with other symbols. If you have that many high count 1:1 substitutes on a key, then you have to stack so many symbols on the other letters that there would be few medium count symbols. It would be a few high count and a lot of low count.

I will show more of my work in the next few days.

EDIT: I guess I did a terrible job of explaining myself. What I am saying is that the statistics show that if Zodiac transposed vertically, it is more likely that the message was a few plaintext less than 323 rather than a few plaintext longer than 323.

Here is where period 19 bigraphs in the beginning of the message have symbols that match period 18 bigraph repeats in the remaining part of the message: