Here is where period 17 bigraphs in the beginning of the message have symbols that match period 18 bigraph repeats in the remaining part of the message. The heavy red line on the scatter graph shows the mean position of the leftmost symbols. The pink lines on the scatter graph show the mean position and standard deviations of 30 mean positions when comparing period 1 to period 31 bigraph lists. The statistics are not highly improbable, I think, but suggest that the message could be less than 323 if Zodiac transposed vertically.

Ah! I think I’m beginning to understand your idea of comparing bigrams of period N with bigrams of period N-1. If the last row is incomplete, for the columns with the empty squares, you’ll essentially be making transposition of width N-1 (since you have 1 fewer rows above). And where the squares are filled, the transposition will be the full width N. Right?

Here is the smokie9 plaintext transposition:

Here is the Key:

A 1 26 48
B 2 27
C 3 28
D 4 29
E 5 30 49 52
F 6 31 50
G 7 32 51
H 8 33 19
I 9 34 53
J
K 10 35 54
L 11 36 55 19
M 12 37 56
N 13 38 57 20
O 14 39 58
P 15 40 59
Q
R 16 41 60 20
S 17 42 61 20
T 18 43 62 19
U 21 44 63
V 22 45
W 23 46
X 24
Y 25 47
Z

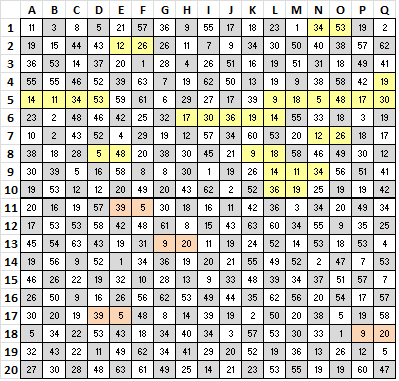
Here is the message as originally posted:

11 3 8 5 21 13 36 34 55 17 18 23 1 34 53 33 27
19 59 44 43 12 1 48 11 7 34 53 30 6 40 38 57 19
36 9 14 37 57 1 28 4 26 32 16 19 7 31 18 49 41
55 19 46 52 39 63 7 19 43 50 20 19 9 20 58 42 33
14 55 53 34 59 61 6 29 27 20 39 9 62 5 48 20 52
23 2 1 46 42 25 7 61 49 11 19 58 55 33 18 3 19
10 27 43 19 4 29 30 56 57 34 60 53 20 12 26 62 42
20 19 3 52 48 20 13 30 45 21 9 18 14 23 49 52 37
5 39 5 16 58 8 33 30 1 36 26 14 11 34 56 51 41
19 9 12 37 60 19 20 43 62 2 52 36 55 47 19 19 42
57 16 19 57 39 5 30 18 41 11 61 19 3 53 20 49 9
17 53 9 58 42 48 61 8 15 43 44 60 9 11 34 35 25
22 54 63 62 55 31 34 42 55 62 24 52 58 34 43 53 4
19 56 9 5 1 34 36 30 20 21 55 49 52 27 47 7 34
23 1 22 19 32 10 3 13 53 33 48 39 34 12 7 38 7
1 50 53 20 26 37 43 9 30 44 35 62 56 16 54 17 57
30 57 19 58 49 48 8 39 39 55 2 6 13 38 19 19 14
5 34 45 53 19 18 34 40 34 28 20 53 30 33 1 53 42
32 43 22 11 49 62 34 41 29 20 52 19 36 13 1 12 5
27 30 28 48 63 61 49 25 14 21 23 53 55 19 19 60 47

And here is smokie9 un-transposed:

53 55 9 10 5 54 9 19 11 9 57 7 59 52 14 59 11
30 2 30 3 1 63 17 19 34 18 34 61 61 39 37 44 3
33 6 44 13 34 62 53 42 56 14 60 49 6 63 57 43 8
1 13 35 53 36 55 9 57 51 23 53 11 29 7 1 12 5
53 38 62 33 30 31 58 16 41 49 20 19 27 19 28 1 21
42 19 56 48 20 34 42 19 19 52 12 58 20 43 4 48 13
32 19 16 39 21 42 48 57 9 37 26 55 39 50 26 11 36
43 14 54 34 55 55 61 39 12 5 62 33 9 20 32 7 34
22 5 17 12 49 62 8 5 37 39 42 18 62 19 16 34 55
11 34 57 7 52 24 15 30 60 5 20 3 5 9 19 53 17
49 45 30 38 27 52 43 18 19 16 19 19 48 20 7 30 18
62 53 57 7 47 58 44 41 20 58 3 10 20 58 31 6 23
34 19 19 1 7 34 60 11 43 8 52 27 52 42 18 40 1
41 18 58 50 34 43 9 61 62 33 48 43 23 33 49 38 34
29 34 49 53 23 53 11 19 2 30 20 19 2 14 41 57 53
20 40 48 20 1 4 34 3 52 1 13 4 1 55 55 19 33
52 34 8 26 22 19 35 53 36 36 30 29 46 53 19 36 27
19 28 39 37 19 56 25 20 55 26 45 30 42 34 46 9 19
36 20 39 43 32 9 22 49 47 14 21 56 25 13 1 12 5
27 30 28 48 63 61 49 25 14 21 23 53 55 19 19 60 47

Ah! I think I’m beginning to understand your idea of comparing bigrams of period N with bigrams of period N-1. If the last row is incomplete, for the columns with the empty squares, you’ll essentially be making transposition of width N-1 (since you have 1 fewer rows above). And where the squares are filled, the transposition will be the full width N. Right?

Right.

Here is smokie9, where I attempted to match 340 stats. I didn’t achieve quite 340 stats, which are a bit more extreme.

O.k., so here is a screenshot of part one of my spreadsheets. This one makes messages, and allows me to randomize each row custom:

And here is a screenshot of part of another spreadsheet. This one allows me to try to solve manually, and shows bigram repeats and bigram repeats by half:

Making messages by transposing the plaintext vertically results in fewer bigram repeats, and it is not difficult at all to make messages with very low bigram repeats by half. The most common bigrams in Zodiac’s letters are TH, HE, IN, ER, IS, LL, etc. With vertical transposition (or any transposition), the letters don’t sit next to each other.

If I randomize smokie9 0% and use perfect cycles, this is what the bigram repeats by half look like:

With randomization, the bigram repeats by half change. With 25% randomization, it took me 5 clicks on "calculate now" to get this:

And it took me another 12 clicks on "calculate now" to get this:

And another 2 clicks on "calculate now" to get this:

So you get the idea.

The bizarre thing, however, is when I increase randomization, the more clicks it takes to get similar results if at all! With higher randomization, I get more bigram repeats by half. And I need to do some more work in the department to gather more information and understand why.

So I decided to score the bigram repeats in different un-transposed versions of the 340 so that I could compare them to each other.

My scoring formula is probability, but made so that the numbers are easy for me to understand and compare:

1/ [ [ ( Symbol A Count / 340 ) * ( Symbol B Count / 340 ) ] ^ Number of Occurrences ] * 100000

Here are the un-transposed versions of the 340, with total bigram repeats and total scores, thinking that the plaintext may be just short of 323 (gibberish in red):

340.322.down.righttoleft
transpose down right to left bigram count 70 score 384,430
21 26 7 56 50 34 36 38 53 19 15 17 17 6 36 5 1
33 20 28 2 16 33 6 19 31 60 8 56 11 44 37 19 2
5 11 32 4 53 19 3 3 55 13 28 10 50 30 19 20 3
11 33 37 8 61 18 41 54 40 47 40 51 51 8 38 21 4
51 13 57 38 28 11 11 50 6 17 13 4 9 45 39 22 5
10 19 15 39 36 50 30 48 38 29 11 16 19 5 15 23 6
17 19 16 50 8 51 53 2 8 37 21 25 52 23 26 24 7
26 33 3 55 53 20 14 11 19 19 15 21 53 19 21 25 8
29 26 36 19 48 36 50 25 7 61 16 22 10 19 33 26 9
43 56 14 11 19 21 37 27 41 19 41 50 54 3 13 27 10
48 40 19 36 19 58 28 20 19 39 32 19 5 31 22 28 11
20 26 13 28 34 44 19 5 23 3 49 31 44 16 40 29 12
46 36 12 45 20 3 52 61 5 16 22 57 3 46 1 30 13
27 9 16 40 59 6 20 14 43 51 23 24 7 47 41 31 14
23 23 56 20 12 15 51 37 29 20 19 58 51 37 42 32 15
20 42 29 31 30 51 40 31 51 36 46 16 6 19 5 33 16
30 1 19 21 35 18 63 23 20 34 18 38 23 40 5 20 17
55 14 51 23 53 7 47 16 34 62 27 36 55 48 43 34 18
56 54 6 5 47 32 42 29 55 63 40 59 30 49 7 35 36
4 37 25 1 18 5 10 42 40 39 23 44 62 11 31 58 19

340.321.down.righttoleft
transpose down right to left bigram count 72 score 3,006,172
54 6 5 47 32 42 29 55 63 40 59 30 49 7 35 5 1
21 26 7 56 50 34 36 38 53 19 15 17 17 6 36 19 2
33 20 28 2 16 33 6 19 31 60 8 56 11 44 37 20 3
5 11 32 4 53 19 3 3 55 13 28 10 50 30 19 21 4
11 33 37 8 61 18 41 54 40 47 40 51 51 8 38 22 5
51 13 57 38 28 11 11 50 6 17 13 4 9 45 39 23 6
10 19 15 39 36 50 30 48 38 29 11 16 19 5 15 24 7
17 19 16 50 8 51 53 2 8 37 21 25 52 23 26 25 8
26 33 3 55 53 20 14 11 19 19 15 21 53 19 21 26 9
29 26 36 19 48 36 50 25 7 61 16 22 10 19 33 27 10
43 56 14 11 19 21 37 27 41 19 41 50 54 3 13 28 11
48 40 19 36 19 58 28 20 19 39 32 18 5 31 22 29 12
20 26 13 28 34 44 19 5 23 3 49 31 44 16 40 30 13
46 36 12 45 20 3 52 61 5 16 22 57 3 46 1 31 14
27 9 16 40 59 6 20 14 43 51 23 24 7 47 41 32 15
23 23 56 20 12 15 51 37 29 20 19 58 51 37 42 33 16
20 42 29 31 30 51 40 31 51 36 46 16 6 19 5 20 17
30 1 19 21 35 18 63 23 20 34 18 38 23 40 5 34 18
55 14 51 23 53 7 47 16 34 62 27 36 55 48 43 56 36
4 37 25 1 18 5 10 42 40 39 23 44 62 11 31 58 19

340.320.down.righttoleft
transpose down right to left bigram count 70 score 716,160
14 51 23 53 7 47 16 34 62 27 36 55 48 43 35 5 1
54 6 5 47 32 42 29 55 63 40 59 30 49 7 36 19 2
21 26 7 56 50 34 36 38 53 19 15 17 17 6 37 20 3
33 20 28 2 16 33 6 19 31 60 8 56 11 44 19 21 4
5 11 32 4 53 19 3 3 55 13 28 10 50 30 38 22 5
11 33 37 8 61 18 41 54 40 47 40 51 51 8 39 23 6
51 13 57 38 28 11 11 50 6 17 13 4 9 45 15 24 7
10 19 15 39 36 50 30 48 38 29 11 16 19 5 26 25 8
17 19 16 50 8 51 53 2 8 37 21 25 52 23 21 26 9
26 33 3 55 53 20 14 11 19 19 15 21 53 19 33 27 10
29 26 36 19 48 36 50 25 7 61 16 22 10 19 13 28 11
43 56 14 11 19 21 37 27 41 19 41 50 54 3 22 29 12
48 40 19 36 19 58 28 20 19 39 32 19 5 31 40 30 13
20 26 13 28 34 44 19 5 23 3 49 31 44 16 1 31 14
46 36 12 45 20 3 52 61 5 16 22 57 3 46 41 32 15
27 9 16 40 59 6 20 14 43 51 23 24 7 47 42 33 16
23 23 56 20 12 15 51 37 29 20 19 58 51 37 5 20 17
20 42 29 31 30 51 40 31 51 36 46 16 6 19 5 34 18
30 1 19 21 35 18 63 23 20 34 18 38 23 40 55 56 36
4 37 25 1 18 5 10 42 40 39 23 44 62 11 31 58 19

340.319.down.righttoleft
transpose down right to left bigram count 61 score 350,426
1 19 21 35 18 63 23 20 34 18 38 23 40 43 35 5 1
14 51 23 53 7 47 16 34 62 27 36 55 48 7 36 19 2
54 6 5 47 32 42 29 55 63 40 59 30 49 6 37 20 3
21 26 7 56 50 34 36 38 53 19 15 17 17 44 19 21 4
33 20 28 2 16 33 6 19 31 60 8 56 11 30 38 22 5
5 11 32 4 53 19 3 3 55 13 28 10 50 8 39 23 6
11 33 37 8 61 18 41 54 40 47 40 51 51 45 15 24 7
51 13 57 38 28 11 11 50 6 17 13 4 9 5 26 25 8
10 19 15 39 36 50 30 48 38 29 11 16 19 23 21 26 9
17 19 16 50 8 51 53 2 8 37 21 25 52 19 33 27 10
26 33 3 55 53 20 14 11 19 19 15 21 53 19 13 28 11
29 26 36 19 48 36 50 25 7 61 16 22 10 3 22 29 12
43 56 14 11 19 21 37 27 41 19 41 50 54 31 40 30 13
48 40 19 36 19 58 28 20 19 39 32 19 5 16 1 31 14
20 26 13 28 34 44 19 5 23 3 49 31 44 46 41 32 15
46 36 12 45 20 3 52 61 5 16 22 57 3 47 42 33 16
27 9 16 40 59 6 20 14 43 51 23 24 7 37 5 20 17
23 23 56 20 12 15 51 37 29 20 19 58 51 19 5 34 18
20 42 29 31 30 51 40 31 51 36 46 16 6 30 55 56 36
4 37 25 1 18 5 10 42 40 39 23 44 62 11 31 58 19

340.322.up.righttoleft
transpose up right to left bigram count score
56 54 6 5 47 32 42 29 55 63 40 59 30 49 7 35 18
55 14 51 23 53 7 47 16 34 62 27 36 55 48 43 34 17
30 1 19 21 35 18 63 23 20 34 18 38 23 40 5 20 16
20 42 29 31 30 51 40 31 51 36 46 16 6 19 5 33 15
23 23 56 20 12 15 51 37 29 20 19 58 51 37 42 32 14
27 9 16 40 59 6 20 14 43 51 23 24 7 47 41 31 13
46 36 12 45 20 3 52 61 5 16 22 57 3 46 1 30 12
20 26 13 28 34 44 19 5 23 3 49 31 44 16 40 29 11
48 40 19 36 19 58 28 20 19 39 32 19 5 31 22 28 10
43 56 14 11 19 21 37 27 41 19 41 50 54 3 13 27 9
29 26 36 19 48 36 50 25 7 61 16 22 10 19 33 26 8
26 33 3 55 53 20 14 11 19 19 15 21 53 19 21 25 7
17 19 16 50 8 51 53 2 8 37 21 25 52 23 26 24 6
10 19 15 39 36 50 30 48 38 29 11 16 19 5 15 23 5
51 13 57 38 28 11 11 50 6 17 13 4 9 45 39 22 4
11 33 37 8 61 18 41 54 40 47 40 51 51 8 38 21 3
5 11 32 4 53 19 3 3 55 13 28 10 50 30 19 20 2
33 20 28 2 16 33 6 19 31 60 8 56 11 44 37 19 1
21 26 7 56 50 34 36 38 53 19 15 17 17 6 36 5 36
4 37 25 1 18 5 10 42 40 39 23 44 62 11 31 58 19

340.321.up.righttoleft
transpose up right to left bigram count 67 score 20,125
55 14 51 23 53 7 47 16 34 62 27 36 55 48 43 34 18
30 1 19 21 35 18 63 23 20 34 18 38 23 40 5 20 17
20 42 29 31 30 51 40 31 51 36 46 16 6 19 5 33 16
23 23 56 20 12 15 51 37 29 20 19 58 51 37 42 32 15
27 9 16 40 59 6 20 14 43 51 23 24 7 47 41 31 14
46 36 12 45 20 3 52 61 5 16 22 57 3 46 1 30 13
20 26 13 28 34 44 19 5 23 3 49 31 44 16 40 29 12
48 40 19 36 19 58 28 20 19 39 32 18 5 31 22 28 11
43 56 14 11 19 21 37 27 41 19 41 50 54 3 13 27 10
29 26 36 19 48 36 50 25 7 61 16 22 10 19 33 26 9
26 33 3 55 53 20 14 11 19 19 15 21 53 19 21 25 8
17 19 16 50 8 51 53 2 8 37 21 25 52 23 26 24 7
10 19 15 39 36 50 30 48 38 29 11 16 19 5 15 23 6
51 13 57 38 28 11 11 50 6 17 13 4 9 45 39 22 5
11 33 37 8 61 18 41 54 40 47 40 51 51 8 38 21 4
5 11 32 4 53 19 3 3 55 13 28 10 50 30 19 20 3
33 20 28 2 16 33 6 19 31 60 8 56 11 44 37 19 2
21 26 7 56 50 34 36 38 53 19 15 17 17 6 36 5 1
54 6 5 47 32 42 29 55 63 40 59 30 49 7 35 56 36
4 37 25 1 18 5 10 42 40 39 23 44 62 11 31 58 19

340.320.up.righttoleft
transpose up right to left bigram count 69 score 2,956,012
30 1 19 21 35 18 63 23 20 34 18 38 23 40 5 34 18
20 42 29 31 30 51 40 31 51 36 46 16 6 19 5 20 17
23 23 56 20 12 15 51 37 29 20 19 58 51 37 42 33 16
27 9 16 40 59 6 20 14 43 51 23 24 7 47 41 32 15
46 36 12 45 20 3 52 61 5 16 22 57 3 46 1 31 14
20 26 13 28 34 44 19 5 23 3 49 31 44 16 40 30 13
48 40 19 36 19 58 28 20 19 39 32 19 5 31 22 29 12
43 56 14 11 19 21 37 27 41 19 41 50 54 3 13 28 11
29 26 36 19 48 36 50 25 7 61 16 22 10 19 33 27 10
26 33 3 55 53 20 14 11 19 19 15 21 53 19 21 26 9
17 19 16 50 8 51 53 2 8 37 21 25 52 23 26 25 8
10 19 15 39 36 50 30 48 38 29 11 16 19 5 15 24 7
51 13 57 38 28 11 11 50 6 17 13 4 9 45 39 23 6
11 33 37 8 61 18 41 54 40 47 40 51 51 8 38 22 5
5 11 32 4 53 19 3 3 55 13 28 10 50 30 19 21 4
33 20 28 2 16 33 6 19 31 60 8 56 11 44 37 20 3
21 26 7 56 50 34 36 38 53 19 15 17 17 6 36 19 2
54 6 5 47 32 42 29 55 63 40 59 30 49 7 35 5 1
14 51 23 53 7 47 16 34 62 27 36 55 48 43 55 56 36
4 37 25 1 18 5 10 42 40 39 23 44 62 11 31 58 19

340.319.up.righttoleft
transpose up right to left bigram count 74 score 716,253
20 42 29 31 30 51 40 31 51 36 46 16 6 19 5 34 18
23 23 56 20 12 15 51 37 29 20 19 58 51 37 5 20 17
27 9 16 40 59 6 20 14 43 51 23 24 7 47 42 33 16
46 36 12 45 20 3 52 61 5 16 22 57 3 46 41 32 15
20 26 13 28 34 44 19 5 23 3 49 31 44 16 1 31 14
48 40 19 36 19 58 28 20 19 39 32 19 5 31 40 30 13
43 56 14 11 19 21 37 27 41 19 41 50 54 3 22 29 12
29 26 36 19 48 36 50 25 7 61 16 22 10 19 13 28 11
26 33 3 55 53 20 14 11 19 19 15 21 53 19 33 27 10
17 19 16 50 8 51 53 2 8 37 21 25 52 23 21 26 9
10 19 15 39 36 50 30 48 38 29 11 16 19 5 26 25 8
51 13 57 38 28 11 11 50 6 17 13 4 9 45 15 24 7
11 33 37 8 61 18 41 54 40 47 40 51 51 8 39 23 6
5 11 32 4 53 19 3 3 55 13 28 10 50 30 38 22 5
33 20 28 2 16 33 6 19 31 60 8 56 11 44 19 21 4
21 26 7 56 50 34 36 38 53 19 15 17 17 6 37 20 3
54 6 5 47 32 42 29 55 63 40 59 30 49 7 36 19 2
14 51 23 53 7 47 16 34 62 27 36 55 48 43 35 5 1
1 19 21 35 18 63 23 20 34 18 38 23 40 30 55 56 36
4 37 25 1 18 5 10 42 40 39 23 44 62 11 31 58 19

I am honestly not totally confident with the scoring and comparisons. One extra bigram repeat with a high score, exponent-ed, can make a big difference. Nevertheless, it is done now.

Sorry, I still don’t quite get what you did with smokie9/10. In this case a few words might be better than a lot of pictures. 🙂 You randomized each row?

So I don’t know if this is the "right" one or not, or if any of them are the "right" one. But let’s take a look at the bigram repeats for the highest scoring un-transposition:

340.321.down.righttoleft
transpose down right to left bigram count 72 score 3,006,172

It will have many of the same bigram repeats as the others. This is a screenshot of one of my spreadsheets that scores the bigram repeats and ranks them:

Symbol 19 is the +.

See the two red boxes? 19 before 15 and 19 before 21. Guess what? 15 cycles with 21. I have a list of 1,953 two symbol cycles, and that one ranks 17th by cycle score:

15 21 15 21 21 15 21 15 21 15 21 15 21

See the two green boxes? 36 before 19 and 53 before 19. Guess what? 36 cycles with 53, and ranks 45th by cycle score:

36 53 36 36 53 36 53 36 53 36 53 53 36 36 36 36

Also note the characteristic randomization at the end of the cycle.

See the two blue boxes? 6 before 19 and 11 before 19. 6 and 11 cycle together, and rank 10th out of 1,953 cycles:

6 11 6 11 6 11 6 11 6 11 11 6 11 6 11 11 11

Again, the characteristic randomization toward the end.

And that is as far as I have gone in the cycle comparison department when comparing ranked bigram repeats of an un-transposed version of the 340 assuming by the cross period bigram statistics that the message could be somewhat less than 323 symbols long…

I have other stuff to talk about, but will take a little break now.

Sorry, I still don’t quite get what you did with smokie9/10. In this case a few words might be better than a lot of pictures. You randomized each row?

I wrote out the message, which was 319 plaintext long. Then I re-drafted with vertical transposition, starting with the rightmost column working to the left. I transposed down. Similar to what we talked about with our simultaneous idea about the 340. Then I encoded the transposed plaintext with cycles, but randomized my symbol selection 25%. I can adjust the randomization BY row if I want to, but uniformly randomized my symbol selection when encoding plaintext to ciphertext from the key. In other words, If 1,2,3, and 4 map to A, I would cycle them, but 25% of the time choose a symbol at random [EDIT: 1,2,3 or 4 at random] instead of sticking with the cycle. If I want to, I could change the randomization so that in rows 11-17, for instance, I select the symbols from the [EDIT: cycles] at random 50%. Or whatever.

EDIT: Here is the key for smokie9 and smokie10:

A 1 26 48
B 2 27
C 3 28
D 4 29
E 5 30 49 52
F 6 31 50
G 7 32 51
H 8 33 19
I 9 34 53
J
K 10 35 54
L 11 36 55 19
M 12 37 56
N 13 38 57 20
O 14 39 58
P 15 40 59
Q
R 16 41 60 20
S 17 42 61 20
T 18 43 62 19
U 21 44 63
V 22 45
W 23 46
X 24
Y 25 47

If I was encoding row 1 and set the randomization in that row to 25%, and then needed to select a symbol for plaintext A, I would select 1, 26, and 48 in that order, cycling them. Except that 25% of the time I would select 1, 26 or 48 at random. The 340 has about 25% to 30% randomization of symbol selection. It seems by looking at individual cycles, randomization increases toward the end of the message. With smokie9 and smokie10, I set the randomization to 25% on each row. I did try to increase the randomization from 0% to 40% from row 1 to row 20. And I tried a lot of other randomization steps by row. However, as I increased the randomization, I would get higher bigram repeats by half in the half that had the higher on average randomization. For instance, if I randomized the first half 10% and the second 40%, I would get fewer bigram repeats in the first half on average rather than the second half. It sounds counter-intuitive, I know, and do not fully understand why. But for smokie9 and smokie10, selected 25% uniformly for each row to match overall 340 cycle stats.

Thanks for asking. I had to provide a lot of information today because I need to do something else tomorrow. If you have any other questions, by all means, ask. I will do my best to explain.

Smokie, you actually un-transposed the smokie9 plaintext (meaning that we would never get it assuming you transposed vertically, while you actually un-transposed, as if the the plaintext was transposed already) and I had my suspicion because of a corresponding bigram peak at 17 by 19. But I’m guessing that was your point, I think you may be on to something.

Maybe "my terminology" (transpose, un-transpose) is not correct in that it’s still a transposition.

These are bigram direction tables for doing transposition (assuming the cipher was un-transposed, in my terms).

smokie9 17 by 20:
Horizontals: 23.83%
Verticals: 30.84%
Diagonals 1: 23.36%
Diagonals 2: 21.96%

So the peak is already there at 17 by 20.

smokie9 17 by 19:
Horizontals: 20.64%
Verticals: 33.02%
Diagonals 1: 22.47%
Diagonals 2: 23.85%

Slightly more pronounced at 17 by 19.

Now a test with the 408 while having the upper 17 by 19 portion un-transposed vertically (perfect example).

408 special 17 by 20:
Horizontals: 24.06%
Verticals: 20.30%
Diagonals 1: 26.31%
Diagonals 2: 29.23%

408 special 17 by 19:
Horizontals: 16.66%
Verticals: 42.22%
Diagonals 1: 20.55%
Diagonals 2: 20.55%

Now the 340 with a surprising result.

340 17 by 20:
Horizontals: 31.03%
Verticals: 20.68%
Diagonals 1: 24.13%
Diagonals 2: 24.13%

340 17 by 19:
Horizontals: 28.72%
Verticals: 38.12% <– indicative of what smokie is suggesting?
Diagonals 1: 16.57%
Diagonals 2: 16.57%

Okay I finally managed to solve the smokie9.

I’ll will try the same for the 340.

Update, edit: have tried all 4 possible vertical transpositions (corners) for up to minus 24, nothing.

Then I re-drafted with vertical transposition, starting with the rightmost column working to the left. I transposed down. Similar to what we talked about with our simultaneous idea about the 340.

Ah, I see, you reversed the order of columns when transposing. So in effect, you used a columnar transposition with the key 19,18,17,..,3,2,1. Which is the reason I couldn’t solve it. And I was worried there was something wrong with my transposition routine. 🙂

Then I encoded the transposed plaintext with cycles, but randomized my symbol selection 25%. I can adjust the randomization BY row if I want to, but uniformly randomized my symbol selection when encoding plaintext to ciphertext from the key. In other words, If 1,2,3, and 4 map to A, I would cycle them, but 25% of the time choose a symbol at random [EDIT: 1,2,3 or 4 at random] instead of sticking with the cycle. If I want to, I could change the randomization so that in rows 11-17, for instance, I select the symbols from the [EDIT: cycles] at random 50%. Or whatever.

Randoms cycles or perfect cycles makes absolutely no difference whatsoever for auto-solvers that we are using, so you shouldn’t dwell on it too much when constructing test ciphers. Unless of course you are testing something about randomness of cycles that you are working on, then please disregard my comment. 🙂