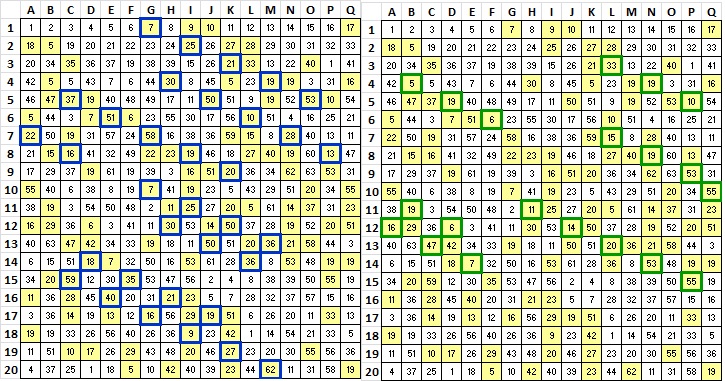
@smokie, I think these lines are just a product of the amount of bigrams at those periods.
Interesting! It makes me curious if periodic trigrams could also be found to correlate to the periodic bigram peaks. Or, instead of trigrams, maybe periodic repeating fragments can also be found at the same periods where bigrams are peaking (the periodic equivalent of, say, the A?B?C type patterns where "?" can be any symbol).
If those kinds of patterns also peak at the same periods, maybe it would be a type of confirmation of the scheme.
I made a new measurement. It compares n-grams in the cipher and when a symbol matches it is counted, to give an example. N-gram size 5: "A1B1C" vs "A2B2C", 3 symbols match so the score for this comparison is 6, 3*(3-1). All n-grams are compared and the scores are summed. Here follow the results:
5-gram comparison for the 408 and 340 in a 17 by 20 grid (do transposition, undo transposition):
408:
Horizontals average: 854, 854
Verticals average: 453, 317
Diagonals 1 average: 376, 409
Diagonals 2 average: 395, 366
340:
Horizontals average: 537, 537
Verticals average: 387, 546
Diagonals 1 average: 423, 496
Diagonals 2 average: 411, 427
Bigram 19 scheme: 630
Bigram 15 scheme: 664
The new measurement is in favor of the scheme, and also when comparing other n-gram sizes.
Another something in favor of the scheme, after expanding all symbols with a count of 10 or higher (7 symbols, 87 occurrences) the peaks are still there.
True. But I am saying that these diagonal rows are words that have more than one English language high frequency bigram in them, or ends of some words abutting beginnings of other words where the ends and beginnings are English language high frequency bigrams.
What does that mean, "expanding all symbols"?
What does that mean, "expanding all symbols"?
Assign a new unique symbol to every occurrence. So I introduced (87 minus 7) new symbols. It was the simplest option to show that the scheme cannot be attributed to some of the strange properties of the more frequent symbols, the whole cipher is in on it so to say.
Ah, I understand now. Thanks. That’s very interesting.
Thanks, all, for all the excellent work you’re all doing to pursue this! I have to again say how great it is for scientifically-minded folks to be actively focused on the 340 for a change. 
5-gram comparison for the 408 and 340 in a 17 by 20 grid (do transposition, undo transposition):
408:
Horizontals average: 854, 854
Verticals average: 453, 317
Diagonals 1 average: 376, 409
Diagonals 2 average: 395, 366340:
Horizontals average: 537, 537
Verticals average: 387, 546
Diagonals 1 average: 423, 496
Diagonals 2 average: 411, 427
Bigram 19 scheme: 630
Bigram 15 scheme: 664The new measurement is in favor of the scheme, and also when comparing other n-gram sizes.
That is really cool. The score is lower for the 340 bigram 15 and 19 schemes as opposed to the 408 horizontals average, but that can probably be attributed to 63 symbols versus 54 symbols.
Do you mind scoring smokie9 if you get the chance. That may be a close interpretation of the 340, I believe.
I started a tracing map for "candy cane" 17×19 but yeah, it’s exactly the same as the tracing map for vertical 17×19. Last night I was really tired, and not sure where to go next.
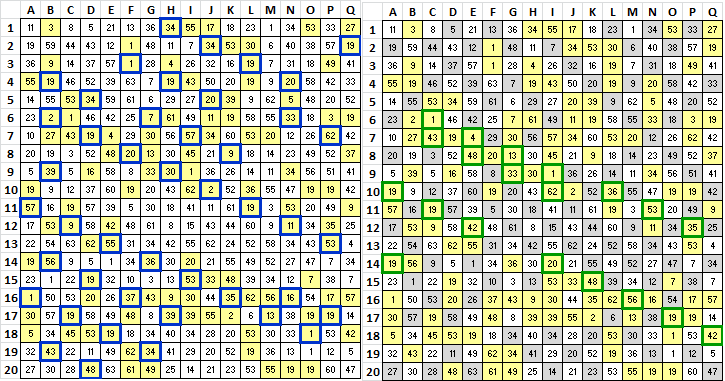
Looking at the chart repeats does the top half have a different structure to the bottom half ..that is they are two spaces apart in a row shift and one in a column shift where as in the bottom half they are only one row apart in column or row shift. Maybe he wrote the code out in two halves used a double shift for the top and a single shift for the bottom half.
Mr. Lowe, I think that you are looking at the blue bordered cells on the left that are diagonally next to each other. Look at them as if they are all period 19 bigrams that line up in diagonal rows sloping downward from left to right. The blue bordered cells that are next to each other are those cells in two contiguous rows.
This is gonna sound nutty, but…
Remember the "prime phobia" phenomenon?
Only one "+" and only "B" (the two most common symbols in the 340) fall on prime positions, which is strongly against expectations.
When I created that slide for my talk, I noticed that many of the prime positions seem to follow roughly diagonal paths. This reminded me of the Ulam spiral, which is a way to see that many prime numbers follow diagonals when written in a rectangular spiral pattern, like this:
https://en.wikipedia.org/wiki/Ulam_spiral
It’d be really strange if this turned out to have some connection to a transposition scheme that makes common symbols tend to avoid roughly diagonal lines.
Yes, I already said it sounded nutty. 
OK, so I took the 340, flipped it horizontally, then applied the period 15 scheme to produce a new ciphertext, which I confirmed has the 40 bigram repeats. Then I saw this interesting pattern:
And here’s another interesting one: A partial pivot!
Can someone confirm that my "untransposed" version of the flipped 340 is correct:
dEB+*5k.L(MVE5FV5 2c+ztZ1*HBpzOUNyB O+l#2E.B)+kN^D(+4 (8KjROp+8zF*K<SBK 2H+M8|CV@K<Ut*5cZ G|TC7z|<z2p+l2_cF KUcy5C^W(cFHl%WO& Dp+fZ+B.;+G1BCOO| G)pclddG+4dl5||.U qLcW<Sk.#KSMF;+B< MF<Sf9pl/C|DpOGp+ 2|5J+JYM(+lXz6PYA TfN:^j*Xz6-z/JNbV M)R)WkPYLR/9^%OF7 TB29^4OFT-+M>#Z3P >L#2b^D4ct+B31c_8 LKJy7t-cYAy-RR+4> f|p+dpVW)+k_Rq#2p b&R6N:(+H*;>R(UVF Fz9G++|TB4-y.LWBO
The pattern from the period 15 scheme shows up again the period 19 scheme (unless I messed it up somehow):
Why would it appear again the same way? Is it just the normal geometrical relationship between the period 15 scheme and the period 19 scheme? Or did I mess up my untransposition?
H+M8|CV@K+l#2E.B) >R(UVFFz9z/JNbVM) |DpOGp+2|<Ut*5cZG +kN^D(+4(G++|TB4- R)WkPYLR/5J+JYM(+ |TC7z|<z28KjROp+8 y.LWBOLKJ9^%OF7TB lXz6PYAG)p+l2_cFK zF*K<SBKdy7t-cYAy 29^4OFT-+pclddG+4 Ucy5C^W(cEB+*5k.L -RR+4>f|pM>#Z3P>L dl5||.UqLFHl%WO&D (MVE5FV52+dpVW)+k #2b^D4ct+cW<Sk.#K p+fZ+B.;+c+ztZ1*H _Rq#2pb&RB31c_8Tf SMF;+B<MFG1BCOO|2 BpzOUNyBO6N:(+H*; N:^j*Xz6-<Sf9pl/C
Here’s another pattern, a reflection that doesn’t advance to the next row:
And another symmetrical repeating fragment:
Might just be noise but I thought I’d point them out.
Doranchak, I will have to look into the prime phobia phenomenon, which I did not know of. I think that it may be a clue about the key and wonder about how statistically significant it is. I think that with 63 symbols packed into a 340 symbol message there are going to be a lot of interesting patterns with practice messages. The + and the B are on my list for being polyalphabetic since they do not appear to be cyclic. They are my symbols 19 and 20.
Here are the diagonals for smokie9, which is my interpretation of the 340 but with only two polyalphabetic symbols. Just as with before, the shaded cells are those with symbols that are in period 19 bigram repeats. A lot of them line up in diagonal groups. Two images shown for clarity.
I honestly don’t know what to do next. Jarlve you have been working really hard on this subject, and if you need anything that I am capable of let me know. I have to gather some thoughts together.
EDIT: Jarlve, you have been working very hard on this and I wonder if you need to rest for a while. If you feel that way, let me know. I may need a little rest. I have some thoughts about some of this that I need to work on.
Do you mind scoring smokie9 if you get the chance. That may be a close interpretation of the 340, I believe.
Averages for smokie9, 5-grams (do, undo):
Horizontals: 572, 572
Verticals: 609, 502
Diagonals 1: 499, 551
Diagonals 2: 481, 593
Bigram 19 scheme: 738
Bigram 15 scheme: 662
Purely by bigrams statistics the smokie9 is probably not a good match for the 340, smokie12 is the closest I could find.
And here is the same image for the 340 (I posted it earlier): 
Can someone confirm that my "untransposed" version of the flipped 340 is correct:
It’s correct. It’s the same as 340m_b15n in the following file.
In my file, the prefix is the input string and the suffix is the output string separated by an underscore.
Prefix:
340n = 340 normal
340m = 340 mirrored
340f = 340 flipped (vertical)
340r = 340 reversed (same as mirrored+flipped)
Suffix (unwrapped interpretation of the bigram 15, 19 thing):
b19n = distance 19 normal
b15m = distance 15 mirrored
etc
results_sub_directory=340_test cipher_information=340n_b19n H+M8|CV@K+l#2E.B) >EB+*5k.L-RR+4>f| pMR(UVFFz9z/JNbVM )|D>#Z3P>Ldl5||.U qLFHpOGp+2|<Ut*5c ZG+kNl%WO&D(MVE5F V52+dp^D(+4(G++|T B4-R)WkVW)+k#2b^D 4ct+cW<SPYLR/5J+J YM(+|TC7zk.#Kp+fZ +B.;+c+ztZ|<z28Kj ROp+8y.LWBO1*H_Rq #2pb&RB31c_8LKJ9^ %OF7TBlXz6PYATfSM F;+B<MFG1BCOO|G)p +l2_cFKzF*K<SBK2B pzOUNyBO6N:(+H*;d y7t-cYAy29^4OFT-+ N:^j*Xz6-<Sf9pl/C pclddG+4Ucy5C^W(c cipher_information=340n_b19m )B.E2#l+K@VC|8M+H |f>4+RR-L.k5*+BE> MVbNJ/z9zFFVU(RMp U.||5ldL>P3Z#>D|) c5*tU<|2+pGOpHFLq F5EVM(D&OW%lNk+GZ T|++G(4+(D^pd+25V D^b2#k+)WVkW)R-4B J+J5/RLYPS<Wc+tc4 Zf+pK#.kz7CT|+(MY jK82z<|Ztz+c+;.B+ qR_H*1OBWL.y8+pOR ^9JKL8_c13BR&bp2# MSfTAYP6zXlBT7FO% p)G|OOCB1GFM<B+;F B2KBS<K*FzKFc_2l+ d;*H+(:N6OByNUOzp +-TFO4^92yAYc-t7y C/lp9fS<-6zX*j^:N c(W^C5ycU4+Gddlcp cipher_information=340n_b19f pclddG+4Ucy5C^W(c N:^j*Xz6-<Sf9pl/C y7t-cYAy29^4OFT-+ pzOUNyBO6N:(+H*;d +l2_cFKzF*K<SBK2B F;+B<MFG1BCOO|G)p %OF7TBlXz6PYATfSM #2pb&RB31c_8LKJ9^ ROp+8y.LWBO1*H_Rq +B.;+c+ztZ|<z28Kj YM(+|TC7zk.#Kp+fZ 4ct+cW<SPYLR/5J+J B4-R)WkVW)+k#2b^D V52+dp^D(+4(G++|T ZG+kNl%WO&D(MVE5F qLFHpOGp+2|<Ut*5c )|D>#Z3P>Ldl5||.U pMR(UVFFz9z/JNbVM >EB+*5k.L-RR+4>f| H+M8|CV@K+l#2E.B) cipher_information=340n_b19r c(W^C5ycU4+Gddlcp C/lp9fS<-6zX*j^:N +-TFO4^92yAYc-t7y d;*H+(:N6OByNUOzp B2KBS<K*FzKFc_2l+ p)G|OOCB1GFM<B+;F MSfTAYP6zXlBT7FO% ^9JKL8_c13BR&bp2# qR_H*1OBWL.y8+pOR jK82z<|Ztz+c+;.B+ Zf+pK#.kz7CT|+(MY J+J5/RLYPS<Wc+tc4 D^b2#k+)WVkW)R-4B T|++G(4+(D^pd+25V F5EVM(D&OW%lNk+GZ c5*tU<|2+pGOpHFLq U.||5ldL>P3Z#>D|) MVbNJ/z9zFFVU(RMp |f>4+RR-L.k5*+BE> )B.E2#l+K@VC|8M+H cipher_information=340m_b15n dEB+*5k.L(MVE5FV5 2c+ztZ2H+M8|CV@K< Ut*5cZG|TC7zG)pcl ddG+4dl5||.UqLcW< STfN:^j*Xz6-z/JNb VM)R)WkLKJy7t-cYA y-RR+4>f|p+dp1*HB pzOUNyBO+l#2E.B)+ kN|<z2p+l2_cFKUcy 5C^W(cFHk.#KSMF;+ B<MF<Sf9pl/C|DPYL R/9^%OF7TB29^4OFT -+MVW)+k_Rq#2pb&R 6N:(+H*;>^D(+4(8K jROp+8zF*K<SBKl%W O&Dp+fZ+B.;+G1BCO O|pOGp+2|5J+JYM(+ lXz6PYA>#Z3P>L#2b ^D4ct+B31c_8R(UVF Fz9G++|TB4-y.LWBO cipher_information=340m_b15m 5VF5EVM(L.k5*+BEd <K@VC|8M+H2Ztz+c2 lcp)Gz7CT|GZc5*tU <WcLqU.||5ld4+Gdd bNJ/z-6zX*j^:NfTS AYc-t7yJKLkW)R)MV BH*1pd+p|f>4+RR-y +)B.E2#l+OByNUOzp ycUKFc_2l+p2z<|Nk +;FMSK#.kHFc(W^C5 LYPD|C/lp9fS<FM<B TFO4^92BT7FO%^9/R R&bp2#qR_k+)WVM+- K8(4+(D^>;*H+(:N6 W%lKBS<K*Fz8+pORj OCB1G+;.B+Zf+pD&O +(MYJ+J5|2+pGOp|O b2#L>P3Z#>AYP6zXl FVU(R8_c13B+tc4D^ OBWL.y-4BT|++G9zF cipher_information=340m_b15f Fz9G++|TB4-y.LWBO ^D4ct+B31c_8R(UVF lXz6PYA>#Z3P>L#2b O|pOGp+2|5J+JYM(+ O&Dp+fZ+B.;+G1BCO jROp+8zF*K<SBKl%W 6N:(+H*;>^D(+4(8K -+MVW)+k_Rq#2pb&R R/9^%OF7TB29^4OFT B<MF<Sf9pl/C|DPYL 5C^W(cFHk.#KSMF;+ kN|<z2p+l2_cFKUcy pzOUNyBO+l#2E.B)+ y-RR+4>f|p+dp1*HB VM)R)WkLKJy7t-cYA STfN:^j*Xz6-z/JNb ddG+4dl5||.UqLcW< Ut*5cZG|TC7zG)pcl 2c+ztZ2H+M8|CV@K< dEB+*5k.L(MVE5FV5 cipher_information=340m_b15r OBWL.y-4BT|++G9zF FVU(R8_c13B+tc4D^ b2#L>P3Z#>AYP6zXl +(MYJ+J5|2+pGOp|O OCB1G+;.B+Zf+pD&O W%lKBS<K*Fz8+pORj K8(4+(D^>;*H+(:N6 R&bp2#qR_k+)WVM+- TFO4^92BT7FO%^9/R LYPD|C/lp9fS<FM<B +;FMSK#.kHFc(W^C5 ycUKFc_2l+p2z<|Nk +)B.E2#l+OByNUOzp BH*1pd+p|f>4+RR-y AYc-t7yJKLkW)R)MV bNJ/z-6zX*j^:NfTS <WcLqU.||5ld4+Gdd lcp)Gz7CT|GZc5*tU <K@VC|8M+H2Ztz+c2 5VF5EVM(L.k5*+BEd cipher_information=340f_b15n >;*H+(:N6R&bp2#qR _k+)WVM+-TFO4^92B T7FO%^9/RLYPD|C/l p9fS<FM<B+;FMSK#. kHFc(W^C5ycUKFc_2 l+p2z<|Nk+)B.E2#l +OByNUOzpBH*1pd+p |f>4+RR-yAYc-t7yJ KLkW)R)MVbNJ/z-6z X*j^:NfTS<WcLqU.| |5ld4+Gddlcp)Gz7C T|GZc5*tU<K@VC|8M +H2Ztz+c25VF5EVM( L.k5*+BEdOBWL.y-4 BT|++G9zFFVU(R8_c 13B+tc4D^b2#L>P3Z #>AYP6zXl+(MYJ+J5 |2+pGOp|OOCB1G+;. B+Zf+pD&OW%lKBS<K *Fz8+pORjK8(4+(D^ cipher_information=340f_b15m Rq#2pb&R6N:(+H*;> B29^4OFT-+MVW)+k_ l/C|DPYLR/9^%OF7T .#KSMF;+B<MF<Sf9p 2_cFKUcy5C^W(cFHk l#2E.B)+kN|<z2p+l p+dp1*HBpzOUNyBO+ Jy7t-cYAy-RR+4>f| z6-z/JNbVM)R)WkLK |.UqLcW<STfN:^j*X C7zG)pclddG+4dl5| M8|CV@K<Ut*5cZG|T (MVE5FV52c+ztZ2H+ 4-y.LWBOdEB+*5k.L c_8R(UVFFz9G++|TB Z3P>L#2b^D4ct+B31 5J+JYM(+lXz6PYA># .;+G1BCOO|pOGp+2| K<SBKl%WO&Dp+fZ+B ^D(+4(8KjROp+8zF* cipher_information=340f_b15f *Fz8+pORjK8(4+(D^ B+Zf+pD&OW%lKBS<K |2+pGOp|OOCB1G+;. #>AYP6zXl+(MYJ+J5 13B+tc4D^b2#L>P3Z BT|++G9zFFVU(R8_c L.k5*+BEdOBWL.y-4 +H2Ztz+c25VF5EVM( T|GZc5*tU<K@VC|8M |5ld4+Gddlcp)Gz7C X*j^:NfTS<WcLqU.| KLkW)R)MVbNJ/z-6z |f>4+RR-yAYc-t7yJ +OByNUOzpBH*1pd+p l+p2z<|Nk+)B.E2#l kHFc(W^C5ycUKFc_2 p9fS<FM<B+;FMSK#. T7FO%^9/RLYPD|C/l _k+)WVM+-TFO4^92B >;*H+(:N6R&bp2#qR cipher_information=340f_b15r ^D(+4(8KjROp+8zF* K<SBKl%WO&Dp+fZ+B .;+G1BCOO|pOGp+2| 5J+JYM(+lXz6PYA># Z3P>L#2b^D4ct+B31 c_8R(UVFFz9G++|TB 4-y.LWBOdEB+*5k.L (MVE5FV52c+ztZ2H+ M8|CV@K<Ut*5cZG|T C7zG)pclddG+4dl5| |.UqLcW<STfN:^j*X z6-z/JNbVM)R)WkLK Jy7t-cYAy-RR+4>f| p+dp1*HBpzOUNyBO+ l#2E.B)+kN|<z2p+l 2_cFKUcy5C^W(cFHk .#KSMF;+B<MF<Sf9p l/C|DPYLR/9^%OF7T B29^4OFT-+MVW)+k_ Rq#2pb&R6N:(+H*;> cipher_information=340r_b19n +-TFO4^92yAYc-t7y d;*H+(:N6OByNUOzp B2KBS<K*FzKFc_2l+ p)G|OOCB1GFM<B+;F MSfTAYP6zXlBT7FO% ^9JKL8_c13BR&bp2# qR_H*1OBWL.y8+pOR jK82z<|Ztz+c+;.B+ Zf+pK#.kz7CT|+(MY J+J5/RLYPS<Wc+tc4 D^b2#k+)WVkW)R-4B T|++G(4+(D^pd+25V F5EVM(D&OW%lNk+GZ c5*tU<|2+pGOpHFLq U.||5ldL>P3Z#>D|) MVbNJ/z9zFFVU(RMp |f>4+RR-L.k5*+BE> )B.E2#l+K@VC|8M+H c(W^C5ycU4+Gddlcp C/lp9fS<-6zX*j^:N cipher_information=340r_b19m y7t-cYAy29^4OFT-+ pzOUNyBO6N:(+H*;d +l2_cFKzF*K<SBK2B F;+B<MFG1BCOO|G)p %OF7TBlXz6PYATfSM #2pb&RB31c_8LKJ9^ ROp+8y.LWBO1*H_Rq +B.;+c+ztZ|<z28Kj YM(+|TC7zk.#Kp+fZ 4ct+cW<SPYLR/5J+J B4-R)WkVW)+k#2b^D V52+dp^D(+4(G++|T ZG+kNl%WO&D(MVE5F qLFHpOGp+2|<Ut*5c )|D>#Z3P>Ldl5||.U pMR(UVFFz9z/JNbVM >EB+*5k.L-RR+4>f| H+M8|CV@K+l#2E.B) pclddG+4Ucy5C^W(c N:^j*Xz6-<Sf9pl/C cipher_information=340r_b19f C/lp9fS<-6zX*j^:N c(W^C5ycU4+Gddlcp )B.E2#l+K@VC|8M+H |f>4+RR-L.k5*+BE> MVbNJ/z9zFFVU(RMp U.||5ldL>P3Z#>D|) c5*tU<|2+pGOpHFLq F5EVM(D&OW%lNk+GZ T|++G(4+(D^pd+25V D^b2#k+)WVkW)R-4B J+J5/RLYPS<Wc+tc4 Zf+pK#.kz7CT|+(MY jK82z<|Ztz+c+;.B+ qR_H*1OBWL.y8+pOR ^9JKL8_c13BR&bp2# MSfTAYP6zXlBT7FO% p)G|OOCB1GFM<B+;F B2KBS<K*FzKFc_2l+ d;*H+(:N6OByNUOzp +-TFO4^92yAYc-t7y cipher_information=340r_b19r N:^j*Xz6-<Sf9pl/C pclddG+4Ucy5C^W(c H+M8|CV@K+l#2E.B) >EB+*5k.L-RR+4>f| pMR(UVFFz9z/JNbVM )|D>#Z3P>Ldl5||.U qLFHpOGp+2|<Ut*5c ZG+kNl%WO&D(MVE5F V52+dp^D(+4(G++|T B4-R)WkVW)+k#2b^D 4ct+cW<SPYLR/5J+J YM(+|TC7zk.#Kp+fZ +B.;+c+ztZ|<z28Kj ROp+8y.LWBO1*H_Rq #2pb&RB31c_8LKJ9^ %OF7TBlXz6PYATfSM F;+B<MFG1BCOO|G)p +l2_cFKzF*K<SBK2B pzOUNyBO6N:(+H*;d y7t-cYAy29^4OFT-+
Why would it appear again the same way? Is it just the normal geometrical relationship between the period 15 scheme and the period 19 scheme? Or did I mess up my untransposition?
I can’t verify this untransposition. It starts the same as 340n_b19n but is misaligned from there.
When I created that slide for my talk, I noticed that many of the prime positions seem to follow roughly diagonal paths. This reminded me of the Ulam spiral, which is a way to see that many prime numbers follow diagonals when written in a rectangular spiral pattern, like this:
I don’t consider it nutty. 
Some 7 years ago I became interested in the prime numbers and that sparked most of my programming work. I managed to re-invent Ulam’s spiral and posted my "discovery" on a forum only to make a fool of myself. So I spent about 2 years with the prime numbers (on my terms) and had at one point a program that was able to factorize large semi-primes up to 50 digits using mainly Fermat’s little theorem. That being said I’m certainly no authority on prime numbers but I have a very good understanding of the problem (eternal geometrization) and what to expect.
When displaying prime numbers in a grid, they will mainly follow straight lines down when the horizontal dimension is an even number (modulo 6) and diagonal lines (patterns) for uneven numbers. Ulam’s spiral is very good way to visualize the prime numbers and I actually derived the idea from Fermat’s little theorem (square numbers).
Yesterday, the thought entered my head that perhaps these prime devoid symbols signify overlapping of 2 periods or similar (example 14, 15). That the scheme he used at one point started to overlap on already filled squares and that instead of moving to another square he *overlapped* and created some symbols especially for this. I guess that when 2 periods overlap, these positions will very likely not be prime.
I honestly don’t know what to do next. Jarlve you have been working really hard on this subject, and if you need anything that I am capable of let me know. I have to gather some thoughts together.
EDIT: Jarlve, you have been working very hard on this and I wonder if you need to rest for a while. If you feel that way, let me know. I may need a little rest. I have some thoughts about some of this that I need to work on.
It’s Blizzcon so I will be less active for a couple of days (I have a virtual ticket).
I would like you to look into something if you feel like. In this image ( ) there is a comparison of 340 bigrams. You can see that there is a peak at 15 (green), 19 (red) and 29 (green). In the smokie12, a similar thing is observed. That is, the double of the peak period is not at its expected period. In a perfectly aligned scheme that peaks at 15, there will also likely be a smaller peak at 30, just because that’s the double of the peak period. In the 340 it can be seen at 29 instead of 30 and the same thing can be seen with the smokie12 (look for the first image in this post). This is actual evidence that some kind of misalignment is going on in the 340. What I’d like you to do is an in-depth comparison of period 15 versus 29 and see what you can find out.
Doranchak, I will have to look into the prime phobia phenomenon, which I did not know of. I think that it may be a clue about the key and wonder about how statistically significant it is. I think that with 63 symbols packed into a 340 symbol message there are going to be a lot of interesting patterns with practice messages. The + and the B are on my list for being polyalphabetic since they do not appear to be cyclic. They are my symbols 19 and 20.
Shuffle experiments show that + will fall only on 0 or 1 prime positions in 3% of shuffles. In 0.7% of shuffles, + and B each fall on 0 or 1 prime positions. So, I can’t easily dismiss the phenomenon as coincidence. More info here: http://www.zodiackillerciphers.com/?p=319
