@smokie,

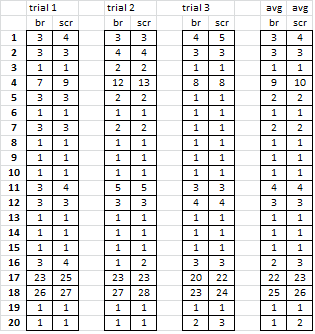
Your idea of randomizing each row a number of times and scoring the averages is really good. This is what I get for my row cipher (1000 randomizations per row). A higher number is a possible indication that the row is gibberish.

Bigram repeats period 19 row randomization test for jarlve_row1.txt.

Row 1: 35
Row 2: 39
Row 3: 37
Row 4: 39
Row 5: 37
Row 6: 39
Row 7: 39
Row 8: 40
Row 9: 38
Row 10: 41
Row 11: 43
Row 12: 44 <---
Row 13: 42
Row 14: 37
Row 15: 38
Row 16: 42
Row 17: 38
Row 18: 36
Row 19: 39
Row 20: 36

This confirms your test for row 12, and indeed row 12 is gibberish. Well done, and yes, it is a transposition cipher with a period 19 scheme. I’ll work on something slightly harder.

340:

Bigram repeats period 19 row randomization test for 340.txt.

Row 1: 35
Row 2: 34
Row 3: 37 <---
Row 4: 35
Row 5: 33
Row 6: 35
Row 7: 32
Row 8: 28
Row 9: 33
Row 10: 35
Row 11: 31
Row 12: 34
Row 13: 32
Row 14: 32
Row 15: 35
Row 16: 32
Row 17: 32
Row 18: 36
Row 19: 35
Row 20: 36

Bigram repeats period 15 row randomization test for 340.txt.

Row 1: 37
Row 2: 39
Row 3: 40 <---
Row 4: 37
Row 5: 37
Row 6: 39
Row 7: 37
Row 8: 33
Row 9: 33
Row 10: 38
Row 11: 36
Row 12: 37
Row 13: 36
Row 14: 37
Row 15: 40 <---
Row 16: 37
Row 17: 36
Row 18: 38
Row 19: 38
Row 20: 37

Row 3 indeed is a good candidate. Interesting.

408:

Bigram repeats period 1 row randomization test for 408.txt.

Row 1: 44
Row 2: 45
Row 3: 45
Row 4: 40
Row 5: 44
Row 6: 44
Row 7: 45
Row 8: 41
Row 9: 42
Row 10: 44
Row 11: 44
Row 12: 41
Row 13: 44
Row 14: 46 <---
Row 15: 42
Row 16: 46 <---
Row 17: 40
Row 18: 41
Row 19: 42
Row 20: 40

New one for smokie:

Edit: to be clear this is a transposition cipher with a period 19 scheme and one row with random filler was inserted after encoding.

1  2  3  4  5  6  7  8  9  9  8  10 11 12 13 14 15
16 11 17 18 19 20 21 22 23 24 25 26 27 28 29 18 30
31 2  32 33 34 31 35 36 37 24 38 10 16 39 5  5  23
40 35 41 24 6  37 42 1  3  43 33 4  14 44 45 45 46
47 20 31 12 48 8  18 49 13 47 25 27 15 38 21 42 50
37 17 18 28 32 33 35 40 11 34 19 24 5  22 35 41 51
29 25 27 8  43 24 30 15 16 36 1  42 10 11 38 45 26
47 21 23 19 5  32 9  6  46 35 7  3  48 36 29 22 20
49 30 3  5  40 45 42 41 18 24 14 49 48 2  52 41 31
45 20 30 31 6  47 40 48 28 9  33 11 43 16 29 21 23
24 12 7  8  25 32 22 43 35 11 49 4  37 15 17 26 34
30 39 28 45 47 48 30 19 13 53 49 49 1  40 54 27 29
7  38 7  33 34 24 3  25 52 21 39 6  16 7  10 22 36
22 27 33 41 17 40 10 11 38 1  32 14 53 15 33 41 52
9  21 45 46 16 32 28 51 4  12 30 2  43 43 26 8  16
9  13 38 31 48 23 39 49 34 35 17 18 39 15 40 2  7
43 9  10 3  9  23 32 38 40 33 10 38 47 22 48 21 28
36 52 24 28 19 21 30 12 25 11 27 19 8  45 42 26 38
10 22 37 4  34 23 13 19 20 17 1  55 41 6  53 14 8
37 42 31 9  41 18 24 40 30 47 28 4  3  2  21 32 49

R$[+4^G?DD?&-',78
(-5#/=aK>Y)9FO#*
L$IEBLS`H>T&("44K
1SU>^HJR[XE+7]::Z
N=L'A?#W,NY98TJ<
H5#FIES1-B/>4aSU2
OY9?X>*8(`RJ&-T:)
NK/4ID^ZSG[A`Oa=
W*[41:JU#>7WA$;UL
:=*L^N1AFDE-X(OK
>'G?YIaXS-W+H85)B
*"F:NA*/,_WWR1V9O
GTGEB>[Y;"^(G&a`
a9EU51&-TRI7_8EU;
D:Z(IF2+'*$XX)?(
D,TLAK"WBS5#"81$G
XD&[DKIT1E&TNaAF
`;>F/*'Y-9/?:J)T
&aH+BK,/=5R0U^_7?
HJLDU#>1*NF+[$IW

.
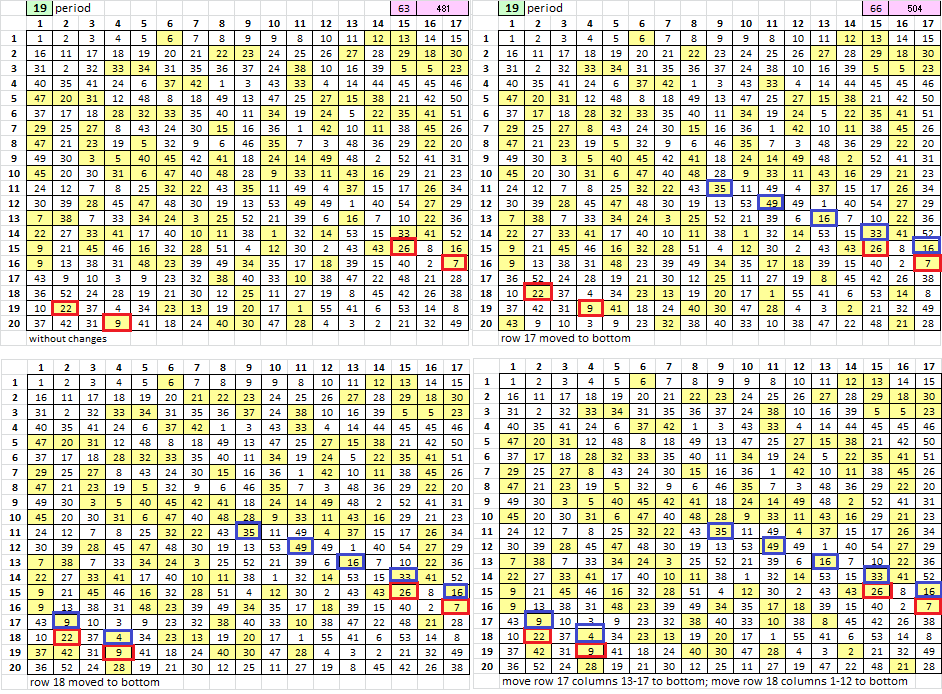
Rows 17 or 18, or the last part of 17 and the first part of 18. Row 4 also shows some signs of gibberish or that there may be a skipped or added symbol, but not nearly as strong as rows 17 and 18. I have been looking at moving row 18 to the bottom, thus shifting row 19 up to be adjacent to row 17. There are at least two continuous diagonal rows of period 19 repeats passing through the area on the left side of the message, making me think that it is more likely row 18, or the beginning of row 18. I have been trying to delete different combinations of end of row 17 and beginning of row 18, and get basically the same results.

I would have to overhaul to my spreadsheet to analyse by position instead of by rows, but also thinking about analyzing columns as well. I had a long day today and am too tired to concentrate on such a big job.

But also thinking it fascinating that shuffles of many of the rows do not result an any increase in period 19 repeats or scores. Is this confirmation of a transposition scheme? How do I articulate the reason why? We really need a message with a high number of period 19 repeats, but not transposition and obviously fewer symbols to compare to. I could try to do that later. I was just, you know, thinking it odd that we have 20 rows and a period of 19, and always assumed that row 20 was the most likely candidate for gibberish given the 408.

Also, I moved row 3 of the 340 to the bottom and shifted the lower rows up. The cycle score dropped a bit, suggesting that if row 3 is gibberish, he would have made it gibberish before encoding the cycles instead of after encoding the cycles. Of course that a big if.

I may play with your message some more in the morning before work if I can.

.

I put up most of those bigrams in the column shift exercise and am intrigued with the amount of cohesion on how they all fit together. I expected to only get a few together, Very few bigrams land apart. Basically I’ve just manipulated a column shift to bring them to a row shift alignment of one. I don’t know what it means if anything, I have stared at it so long I can see Homer Simpson’s face in it. I don’t wish to hijack your good work with clutter so I’ll leave it be for now..

Edit ,, sorry it’s so blurry I had to make the file smaller so it wouldn’t get rejected again. (sorted – trav) Thanks for that Trav.

But also thinking it fascinating that shuffles of many of the rows do not result an any increase in period 19 repeats or scores. Is this confirmation of a transposition scheme? How do I articulate the reason why? We really need a message with a high number of period 19 repeats, but not transposition and obviously fewer symbols to compare to. I could try to do that later. I was just, you know, thinking it odd that we have 20 rows and a period of 19, and always assumed that row 20 was the most likely candidate for gibberish given the 408.

It is confirmation of the statistical significance of the bigram period 15, 19 thing. And to me it seems more likely this is evidence of transposition rather than it being a statistical outlier. As you stated earlier, row 20 is somewhat important, I’ve also noticed this in relation to the bigram 15, 19 thing.

@Mr lowe,

I have looked at such a column shift as well in relation to the bigram period 15-19 thing. I think it’s worth exploring.

Here is the 408 with the following column offsets resulting in a bigram peak at period 17 (and 15 mirrored). Column 2 downshifted by 1, Column 3 downshifted by 2, incrementing etc.

Column 1: 0
Column 2: 1
Column 3: 2
Column 4: 3
Column 5: 4
Column 6: 5
Column 7: 6
Column 8: 7
Column 9: 8
Column 10: 9
Column 11: 10
Column 12: 11
Column 13: 12
Column 14: 13
Column 15: 14
Column 16: 15
Column 17: 16

1  2  3  4  5  6  7  8  9  10 9  11 9  12 13 13 14
15 16 11 17 15 18 19 20 9  21 11 21 18 22 23 7  24
22 25 26 27 23 4  28 11 25 22 29 28 30 19 31 23 20
13 32 33 28 14 19 34 1  35 15 30 25 36 12 37 1  38
38 24 14 11 2  39 5  40 16 41 42 29 18 43 23 38 7
36 12 28 12 27 28 18 33 7  16 44 33 45 39 32 35 40
23 33 9  1  19 14 19 34 34 8  2  46 25 21 37 47 37
9  29 4  22 7  48 40 20 3  10 5  6  27 3  2  49 45
5  10 50 27 2  20 38 35 16 14 14 33 45 16 50 24 27
20 2  28 48 44 32 26 41 1  38 45 4  36 26 16 51 26
2  26 39 26 14 1  10 51 4  37 51 1  34 1  7  48 26
48 5  44 4  7  18 39 31 23 3  26 23 16 12 45 20 22
26 1  52 23 52 20 30 48 42 45 50 36 49 7  13 1  25
31 17 44 51 33 48 36 51 21 52 19 29 39 52 9  4  20
46 48 22 23 25 53 21 43 8  35 40 16 47 54 43 50 15
12 19 54 8  34 15 49 15 4  4  4  37 6  14 4  49 34
29 49 52 32 23 3  48 35 4  18 27 43 25 23 44 14 20
52 38 13 38 38 19 14 17 42 54 37 20 8  15 30 17 11
16 11 21 31 45 17 50 31 33 29 8  22 3  17 11 4  21
25 51 43 13 30 1  1  16 42 50 24 17 19 47 46 8  18

9ZTqcf#8LdLeL^SSY
W%e5WEUBL)e)EMR#(
MVPGRq/eVMN/lUrRB
SJ+/YU_96WlV@^H9k
k(YeZKcF%7NEXRk#
@^/^G/E+#%D+AKJ6F
R+L9UYU__8ZzV)HQH
LNqM#IFBTdcfGTZ=A
cdtGZBk6%YY+A%t(G
BZ/IDJP79kAq@P%OP
ZPKPY9dOqHO9_9#IP
IcDq#EKrRTPR%^ABM
P9pRpBlIAt@=#S9V
r5DO+I@O)pUNKpLqB
zIMRVj)X86F%Q!XtW
^U!8_W=WqqqHfYq=_
N=pJRTI6qEGXVRDYB
pkSkkUY5!HB8Wl5e
%e)rA5tr+N8MT5eq)
VOXSl99%t(5UQz8E

Hi jarlve..if you get time can you run the above through your solver.. Just from row two down to row 16.. Just to see what shows up..

.
Most likely row 18, but also row 17.

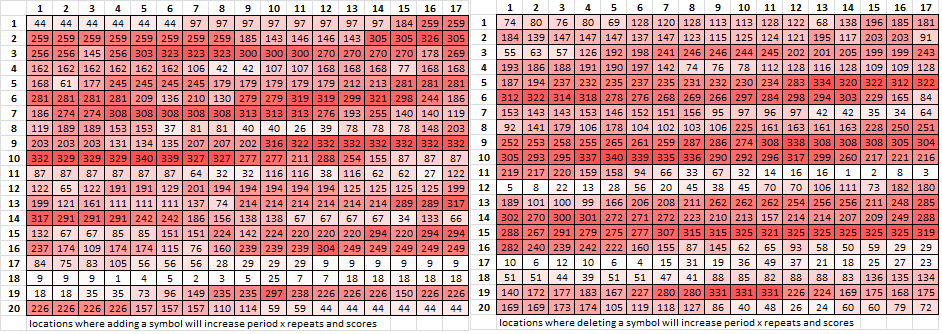
I ran it through the heatmap, although the spreadsheet only shows where adding or deleting one symbol will make a difference. Rows 17 and 18 showed up hot.

Perhaps there is a skipped symbol at row 4, and deleting an extra symbol at row 11 would increase the number of period 19 repeats and/ or score. But the heatmap spreadsheet often times would not show exactly what you did.

Then I moved row 17 to the bottom, row 18 to the bottom, and the last 5 symbols of row 17 and first 12 symbols of row 18 to the bottom. Look at the symbols marked in red. They are two separate pairs of repeats that exist before and after moving any rows, even though they line up in a diagonal row after moving rows 17 or 18.

When I move row 18 to the bottom, then the diagonal row marked in blue is extended. Most likely row 18.

.

Also, I moved row 3 of the 340 to the bottom and shifted the lower rows up. The cycle score dropped a bit, suggesting that if row 3 is gibberish, he would have made it gibberish before encoding the cycles instead of after encoding the cycles. Of course that a big if.

I’ve ran some tests myself to check this and I agree.

Hi jarlve..if you get time can you run the above through your solver.. Just from row two down to row 16.. Just to see what shows up..

Both score lower than the base 340 per cipher length (so very probably not any kind of solve here). Your string is somewhat interesting because there are 39 bigram period 2 repeats. How did you do that?

Score: 20016 Ioc: 770 M: 185 C: 340 S: 63

sistimetiplassion
offaastintheheadc
allerrdanalantern
edithnotieforerro
rlistreetroidsmal
losandheshatswydt
mdelcomieelechale
ctionstostatemiah
airstsandmalesedi
tsitinfitthinchss
trendononceatants
esoramseaftenttie
rsheintollanuitar
ryforfaceshemanal
dieorallseerancle
namployeartswiths
ieasurunateernlea
seouosterondsmina
nsdallonautorilso
thiscradducesmrle

HM+>M#OZG3p)++Rk/
NE:B^+U*V5FOF&4D(
Bppczl8d|dCPV>2L|
SyM7Ftj-*cXkz.zL9
_pR+qlO2U_NGy+@4K
p9+^f%;O+FBY<A6y-
#82Kbj#R2OpcbFBKO
(5MJV+ZJ+YB7.TMBF
dGl+5+^|DT4pc+&8R
-<RURtE*55FMV(;++
Uzc/yJ|N|b.BU4t-+
2+9l^#+24E>cfZ5G2
z<FS*f59Cp^VWMq)L
l6XNz:4(O+F.TB|)p
yG.1LBKC<OSlB/(Cc
|BT3C16cP_YHA*-;+
Rc)+WzWtBZOOL|K2d
+ckWN<7Szk|8<TGf)
|+DdppkVPWY1L*KHJ
>FRH(l^%DW(.+#zK2


Score: 21649 Ioc: 692 M: 247 C: 255 S: 63

tdrawomainningeis
asstahughgeriarch
groundscatswasact
useofhirmuterover
stowillionallmerc
hurrisheristinari
snotiontolaustoan
gehonowhitestogue
clemeddannnoisloo
maturththisamedco
rothwhoredatinner
alngainteswinofac
hestaresionstahas
resscarelighauset
hathesetrulymaclo

NE:B^+U*V5FOF&4D(
Bppczl8d|dCPV>2L|
SyM7Ftj-*cXkz.zL9
_pR+qlO2U_NGy+@4K
p9+^f%;O+FBY<A6y-
#82Kbj#R2OpcbFBKO
(5MJV+ZJ+YB7.TMBF
dGl+5+^|DT4pc+&8R
-<RURtE*55FMV(;++
Uzc/yJ|N|b.BU4t-+
2+9l^#+24E>cfZ5G2
z<FS*f59Cp^VWMq)L
l6XNz:4(O+F.TB|)p
yG.1LBKC<OSlB/(Cc
|BT3C16cP_YHA*-;+

Jarlve,Smokie ,doranchak and crew, this is the visual of column shift and column odds and evens shift (1,3,5,7,9,11then 2, 4, 6, 8,10,12)that wraps around or joins at 17 and 2 with the + and ‘c’. It brings the 19 bigram repeats to pure bigrams Not sure if I should slide the even row2 down one or not.

I think this odd even move brought everything together.i have to leave this up to you gurus now.
by my figuring in my head I should get a similar but different result ..if I use the same process in row shift and odd even shift..
can someone flip this pic to the vertical please.

@smokie,

It’s really cool that your heat map can pick up on that. Row 17 was inserted as random filler after encoding.

Here’s another one for columns and this time it was inserted before encoding.

1  2  3  4  5  6  7  8  9  10 11 12 13 14 15 16 17
18 19 1  20 21 21 8  22 23 3  24 25 26 27 28 29 30
31 4  32 33 34 35 15 36 22 37 1  30 35 38 39 11 5
40 41 42 26 43 6  15 10 24 13 38 44 45 7  12 14 27
39 34 2  24 23 22 3  32 41 28 4  46 47 48 40 21 9
33 30 20 34 21 1  10 13 49 43 2  5  11 44 25 49 16
29 1  37 30 19 47 9  45 50 11 16 42 6  31 14 20 27
25 50 18 4  23 48 46 49 10 13 17 33 32 35 17 29 31
34 26 41 15 40 28 30 47 44 14 21 45 22 27 7  23 48
37 9  50 43 42 38 25 6  16 1  20 31 19 47 3  28 45
5  29 50 1  26 34 30 37 9  46 11 19 31 15 33 12 50
2  22 39 44 26 4  32 42 31 23 24 15 10 33 22 44 6
16 41 11 38 20 7  23 39 43 46 26 3  24 47 34 29 13
49 25 14 2  32 37 15 38 40 48 5  7  22 45 42 33 27
6  11 26 9  25 20 41 15 29 40 49 3  8  50 39 4  22
10 37 43 2  13 24 5  35 42 6  14 16 27 18 44 26 47
19 45 48 4  20 32 46 41 19 10 17 49 12 30 34 13 7
31 14 17 27 3  38 17 29 23 43 8  35 8  9  33 4  16
25 45 10 18 49 50 12 40 37 17 5  42 2  6  13 15 14
44 30 23 39 25 20 49 22 27 7  24 29 31 35 37 32 41

CJPB-)"9WY:DRZ0#;
!EC7119'P+2>(/VI
ABQ[8K0L'3CIK?,:-
&G4>M)0Y+R?HO"DZ(
,8J+'PQG/BN<=&1W
[I781CYRSMJ-:H2S#
VC3IE<WO@:#4)AZ7(
2@!B=NSYR;[QK;VA
8>G0&/I<HZ1O'("=
3W@M4?2)#C7AE<P/O
-V@C>8I3WN:EA0[D@
J',H>BQ4A+0Y['H)
#G:?7",MN>P+<8VR
S2ZJQ30?&=-"'O4[(
):>W27G0V&SP9@,B'
Y3MJR+-K4)Z#(!H><
EO=B7QNGEY;SDI8R"
AZ;(P?;VM9K9W[B#
2OY!S@D&3;-4J)R0Z
HI,27S'("+VAK3QG

@Mr lowe,

I’d say that’s a rather original interpretation and you did bring down the period 19 bigrams to period 1. I moved down your even columns by 1 as you mentioned because that gives the highest bigram count. It doesn’t solve though.

So the operations here are a column period 2 and an incremental per column (0,1,2,3…) up-shift. 38 bigrams.

H+M8|CV@Kz/JNbVM)
N:^j*Xz6-+l#2E.B)
BpzOUNyBO<Sf9pl/C
SMF;+B<MF6N:(+H*;
_Rq#2pb&RG1BCOO|2
p+fZ+B.;+B31c_8Tf
#2b^D4ct+c+ztZ1*H
(MVE5FV52cW<Sk.#K
dl5||.UqL+dpVW)+k
-RR+4>f|pFHl%WO&D
Ucy5C^W(cM>#Z3P>L
29^4OFT-+EB+*5k.L
zF*K<SBKdpclddG+4
lXz6PYAG)y7t-cYAy
y.LWBOLKJp+l2_cFK
|TC7z|<z29^%OF7TB
R)WkPYLR/8KjROp+8
+kN^D(+4(5J+JYM(+
|DpOGp+2|G++|TB4-
>R(UVFFz9<Ut*5cZG

Very interesting, Mr. Lowe and Jarlve. The first line of Jarlve’s transcription looked familiar so I looked through my transposition explorer results and found a set of operations that yields a similar result:

Original: 

HER>pl^VPk|1LTG2d
Np+B(#O%DWY.<*Kf)
By:cM+UZGW()L#zHJ
Spp7^l8*V3pO++RK2
_9M+ztjd|5FP+&4k/
p8R^FlO-*dCkF>2D(
#5+Kq%;2UcXGV.zL|
(G2Jfj#O+_NYz+@L9
d<M+b+ZR2FBcyA64K
-zlUV+^J+Op7<FBy-
U+R/5tE|DYBpbTMKO
2<clRJ|*5T4M.+&BF
z69Sy#+N|5FBc(;8R
lGFN^f524b.cV4t++
yBX1*:49CE>VUZ5-+
|c.3zBK(Op^.fMqG2
RcT+L16C<+FlWB|)L
++)WCzWcPOSHT/()p
|FkdW<7tB_YOB*-Cc
>MDHNpkSzZO8A|K;+

After applying column period 2:

HRp^P|LGdE>lVk1T2
N+(ODY<K)pB#%W.*f
B:MUG(LzJyc+ZW)#H
Sp^8Vp+R2p7l*3O+K
_Mzj|F+4/9+td5P&k
pRFO*CF2(8^l-dk>D
#+q;UXVz|5K%2cG.L
(2f#+Nz@9GJjO_Y+L
dMbZ2By6K<++RFcA4
-lV^+p<B-zU+JO7Fy
UR5EDBbMO+/t|YpTK
2cR|54.&F<lJ*TM+B
z9y+|Fc;R6S#N5B(8
lF^54.Vt+GNf2bc4+
yX*4C>U5+B1:9EVZ-
|.zKO^fq2c3B(p.MG
RTL6<FW|Lc+1C+lB)
+)CWPST(p+WzcOH/)
|kW7BYB-cFd<t_O*C
>DNkzOAK+MHpSZ8|;

After flipping horizontally:

2T1kVl>EdGL|P^pRH
f*.W%#Bp)K<YDO(+N
H#)WZ+cyJzL(GUM:B
K+O3*l7p2R+pV8^pS
k&P5dt+9/4+F|jzM_
D>kd-l^8(2FC*OFRp
L.Gc2%K5|zVXU;q+#
L+Y_OjJG9@zN+#f2(
4AcFR++<K6yB2ZbMd
yF7OJ+Uz-B<p+^Vl-
KTpY|t/+OMbBDE5RU
B+MT*Jl<F&.45|Rc2
8(B5N#S6R;cF|+y9z
+4cb2fNG+tV.45^Fl
-ZVE9:1B+5U>C4*Xy
GM.p(B3c2qf^OKz.|
)Bl+C1+cL|WF<6LTR
)/HOczW+p(TSPWC)+
C*O_t<dFc-BYB7Wk|
;|8ZSpHM+KAOzkND>

Applied diagonal path:

2Tf1*Hk.#KVW)+kl%
WO&D>#Z3P>LEB+*5k
.LdpclddG+4G)y7t-
cYAyLKJp+l2_cFK|<
z29^%OF7TBPYLR/8K
jROp+8^D(+4(5J+JY
M(+pOGp+2|G++|TB4
-R(UVFFz9<Ut*5cZG
H+M8|CV@Kz/JNbVM)
N:^j*Xz6-+l#2E.B)
BpzOUNyBO<Sf9pl/C
SMF;+B<MF6N:(+H*;
_Rq#2pb&RG1BCOO|p
+fZ+B.;+B31c_8#2b
^D4ct+c+ztZ(MVE5F
V52cW<Sdl5||.UqL+
dp-RR+4>f|pFHUcy5
C^W(cM29^4OFT-+zF
*K<SBKlXz6PYAy.LW
BO|TC7zR)Wk+kN|D>

After shifting up 8 rows:

H+M8|CV@Kz/JNbVM)
N:^j*Xz6-+l#2E.B)
BpzOUNyBO<Sf9pl/C
SMF;+B<MF6N:(+H*;
_Rq#2pb&RG1BCOO|p
+fZ+B.;+B31c_8#2b
^D4ct+c+ztZ(MVE5F
V52cW<Sdl5||.UqL+
dp-RR+4>f|pFHUcy5
C^W(cM29^4OFT-+zF
*K<SBKlXz6PYAy.LW
BO|TC7zR)Wk+kN|D>
2Tf1*Hk.#KVW)+kl%
WO&D>#Z3P>LEB+*5k
.LdpclddG+4G)y7t-
cYAyLKJp+l2_cFK|<
z29^%OF7TBPYLR/8K
jROp+8^D(+4(5J+JY
M(+pOGp+2|G++|TB4
-R(UVFFz9<Ut*5cZG

Here's the same with Jarlve's transcripton of Mr. Lowe's cipher to the right for comparison:

H+M8|CV@Kz/JNbVM)    H+M8|CV@Kz/JNbVM)
N:^j*Xz6-+l#2E.B)    N:^j*Xz6-+l#2E.B)
BpzOUNyBO<Sf9pl/C    BpzOUNyBO<Sf9pl/C
SMF;+B<MF6N:(+H*;    SMF;+B<MF6N:(+H*;
_Rq#2pb&RG1BCOO|p    _Rq#2pb&RG1BCOO|2
+fZ+B.;+B31c_8#2b    p+fZ+B.;+B31c_8Tf
^D4ct+c+ztZ(MVE5F    #2b^D4ct+c+ztZ1*H
V52cW<Sdl5||.UqL+    (MVE5FV52cW<Sk.#K
dp-RR+4>f|pFHUcy5    dl5||.UqL+dpVW)+k
C^W(cM29^4OFT-+zF    -RR+4>f|pFHl%WO&D
*K<SBKlXz6PYAy.LW    Ucy5C^W(cM>#Z3P>L
BO|TC7zR)Wk+kN|D>    29^4OFT-+EB+*5k.L
2Tf1*Hk.#KVW)+kl%    zF*K<SBKdpclddG+4
WO&D>#Z3P>LEB+*5k    lXz6PYAG)y7t-cYAy
.LdpclddG+4G)y7t-    y.LWBOLKJp+l2_cFK
cYAyLKJp+l2_cFK|<    |TC7z|<z29^%OF7TB
z29^%OF7TBPYLR/8K    R)WkPYLR/8KjROp+8
jROp+8^D(+4(5J+JY    +kN^D(+4(5J+JYM(+
M(+pOGp+2|G++|TB4    |DpOGp+2|G++|TB4-
-R(UVFFz9<Ut*5cZG    >R(UVFFz9<Ut*5cZG

I suspect there is a set of operations that would produce a closer match, as many sets of operations are equivalent to other sets of operations.

moving the no 2 column down might not be the answer jarlve. it is the wrap around part that I like with the +and `c`.
I think I will get similar results doing the same thing when I do the same with row shift and odd even separation.