Yes, first half is perfectly cyclic and second half is fully random (starting from character position 171). Well done! Since your system is able to detect it I will say that the m2 is more of the same, just that it is the other way around.

I concur. 🙂 Here’s the "sliding window" test using variance of same symbol distances

M1 shows clear increase in the variance (red line) towards the end, which suggest much more random cycles in the second half:

This test is less conclusive for M2, but still shows somewhat higher randomness in the beginning of the cipher (could be because of the plaintext being more random in the second half, considering the bigram IoC dropped towards the end as well):

I’m thinking about a way to maybe exclude wildcard. It may be a bit of work for me and take some time. My spreadsheet finds the positions of all of the cycle symbols. So I was thinking about making a list of the longer cycles that have one or maybe two missing symbols. Then make a list of the strings of symbols between the positions where the missing symbol should be. For ABABABBA, find the string of symbols between the two B’s. Make a list of all of those, and compare to see what symbols are in those strings. The King Bahler paper sort of gave me the idea. The problem is that there are four alleged wildcards of total count over 50, and I don’t want to try to make an experiment to confirm. But, there may be other symbols that are common to those strings, or maybe we can exclude some of the alleged wildcards. I don’t know; it’s just a thought.

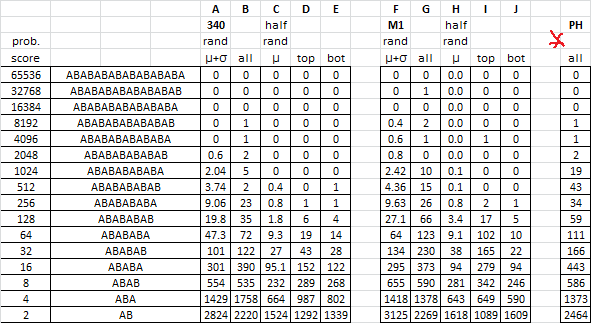
I was really surprised to see how cyclic the 340 is compared to M1. There are two on the M1 perfect cycle list that need to be scratched off because they are parts of cycles that Jarlve made, which makes the M1 perfect cycle list even shorter.

I don’t know what to think of it but what comes to mind is this line in the old FBI documents: "Hand anagramming done with the message as written and on assumptions that message backwards, written columnary, first line forward and second line backward etc."

I’m curious about which FBI document you are referring to in particular? I tried googling the line, and the only result was this message thread (google seems to be getting more useless with every year).

I’m not sure what they mean with columnary, do they mean vertical instead of horizontal?

I think the line you quoted just lists different possible routes, one after another. First "message as written" (i.e. left-to-right, top-to-bottom), then "message backwards" (i.e. reversed), then "written columnary" (i.e. reading by columns, up/down), then "first line forward and second line backward" (i.e. snake path, or plow path).

Hope that helps.

It still doesn’t explain what you mean by "polyalphabetic". I’m familiar with the term, I’m just not sure how a single symbol can be polyalphabetic? In any case, the wildcard theory is pretty straightforward. Please correct me if I got anything wrong. The idea is that some symbols in the cipher don’t represent a particular letter, but represent "any letter". Sort of like "fill in the blanks". I see a couple of issues with it, so I thought I’ll share. Please don’t take it as me trying to shoot down your, and smokie treats’, theory. It’s just a constructive criticism, which will hopefully lead to an improvement in some way.

The first issue, you would need to use a pretty large number of wildcard symbols to confuse the cracking attempts, that’s pretty much a given. For example, Z408 has a few errors in the encryption, which can be viewed as pseudo-wildcards and yet it gets solved with ZDK/AZD quite easily. Which means you need much more real wildcards to make it harder to crack. But would that make the cipher practically impossible to decrypt correctly even if the key is known? What I mean is, if you decrypt to "KIL*", it is probably a safe bet that he is not talking about KILNs or KILTs. But what about "*INE"? Is it LINE? NINE? MINE? Or PINE? You can probably infer based on context. But what if the previous and the next words also have wildcards, and you can’t establish a reliable context? Furthermore, if you don’t have the word boundaries, everything becomes even more ambiguous. Soon you arrive in the anagramming territory, where you can spell out many different things limited only by your imagination. 🙂

But let’s for a second assume that Z didn’t really care if his cipher can be reliably and unambiguously decrypted. Or maybe he used "polyphonic" substitutions, where the same symbol represents more than one letter, but a very limited number of letter. Such as I/J resolve to the same symbol, or U/V, etc.. That should cut down the ambiguity quite a bit.

That’s where the second, and probably more important issue comes in. Wildcards are bound to increase the number of repeating bigrams over the average. Reason being, if you have a text: "BBCBACA", which doesn’t have any bigram repeats, and then you add 2 wildcards like this: "B*CB*CA", you now have 2 repeating bigrams "*C" and "B*". And we are seeing the exact opposite in Z340, which has a lower than expected number of bigram repeats. Pretty much the only reliable way to avoid creating new bigrams is to replace the same letter with the same wildcard symbol each time, but then it wouldn’t be a wildcard any more. To get the low bigram repeats that Z340 has, you would definitely have to be intentionally careful about creating new bigrams with wildcards, and I doubt Z even knew about what a bigram repeat is.

This is what I am guessing that he did; see if you can read it:

W H E N * O U A R E A N G R Y Y O
U * * * O T I O N S A R E L I K E
* U G E W * V E S D U R I N G A S
T * * M A N D Y O U * A * * O T H
E A R * O U R I N T * I * I O N T
* E S A * E W A Y T H A * Y O U C
A N * O T H E A R T H E H U M P B
A C K W H A L E * U N D E * W A T
E R S * D * E S S * * J E A L O U
S Y O R V * N G * F * L L * * S S
A * F E C T S H E A * * N G I N T
I U T I O N I T I S L I K * T * *
I N G T O H * A R A * * I E N D O
N T * E P H O N E W H E N P E * *
L * I N T H E R O O M A R E D A *
C I N G T * L O U * M U S I C O R
C H E * R I N G A * * L L * A M E
* * T H E T E L E V I S I O N Y *
U * F R I E N D * S S P * A K I N
G B U T Y * U C A N N O T H E A *

On the number of bigram repeats issue, I honestly don’t know. I guess what you are saying could be tested. The 340 is pretty darn cyclic. So I guess the answer to your thinking is to create a 63 symbol message with a lot of cyclic ciphertext groups. Include five or six symbols with count 9 to 10 that are in two to four respective cycles, one polyphonic symbol count of 24 randomly placed, and three other polyphonic symbols each with count 10-12 randomly placed. See what happens to the number of expected bigrams. If you are correct, then the number of bigrams will be higher than what you are finding with the 340.

With the wildcard hypothesis, Zodiac encoded the message in one of two ways. He either was encoding and just plopped down q’s, +’s, B’s and F’s (or maybe a different combination of symbols) instead of the symbols that were next in the cycle, or he made a first draft with cycles and then made a second draft with the polyphonic symbols plopped down. Result: difficult to solve. It would have been so easy to do.

By the way, I wonder if the pattern above is one that we could trace with ZKD. If we could take snapshots of the solving process and make a little movie that we could step through forward and backwards. Sometimes the solver finds little strings of words that appear and then disappear. I wonder if the little strings of words appear in certain locations more often than others. If there is a pattern. Has anybody ever tried to do that?

@daikon,

FBI docs: viewtopic.php?f=81&t=2059

I think the line you quoted just lists different possible routes, one after another.

Ah yes, thanks.

The first issue, you would need to use a pretty large number of wildcard symbols to confuse the cracking attempts, that’s pretty much a given.

Depends on how much the n-grams are interrupted, we tested in previous thread that 40-50 symbols will certainly do. Which was about the count of the 4 wildcards suggested. When these symbols are then removed the problem persists.

Wildcards are bound to increase the number of repeating bigrams over the average.

Yes, but not relative to other directions.

You are getting me interested in the bigrams. After thinking about what daikon said, maybe Zodiac didn’t just plop down random wildcards.

Here is a scenario that can be tested ( or maybe already has been ):

1. Zodiac created a cipher key like the one for the 408, with cycles.

2. He encoded his message.

3. Then he visually checked for repeating bigrams and circled them.

4. Then, with his little menu of wildcards, he worked his way down the message from top to bottom, replacing one of the two symbols in each repeated bigram by marking over one of the existing symbols with a wildcard.

5. On a separate piece of paper, he kept a list of the two newly created bigrams, a sequence of three numbers (e.g. 6 19 36). Each time he added a wildcard, he checked above on the list to make sure that he wasn’t repeating any bigrams that he had just created in the message above. If so, then he just switched to the next wildcard on his menu. EDIT: The primary wildcard was +. When adding a + created a new repeating bigram, then he switched to the B or the F. In the beginning of the masking process, using a new wildcard was easy because he had not used that number before. The longer the list for each wildcard, the more difficult it became.

6. Then he made a second draft, with the wildcards, which is the one that we are so familiar with.

Something like that. Maybe he did know what a repeating bigram was. He knew about frequency analysis.

EDIT: I tried it and came up with a message that is more cyclic than the 340, but has much fewer repeating bigrams than the 340 (Only 20 count). There are four wildcards, with counts 21, 9, 8 and 5 for a total of 43 symbols. It won’t solve. If anyone is interested, I highly encourage them to try the process for themselves to see how Zodiac would have done such a thing. I used my computer to identify the repeating bigrams so that I didn’t have to do it visually. If you want to see the cipher key, message grid, and statistics, let me know. I don’t want to post it without permission because it’s not in the suite.

Also note that in doranchak’s list of repeating bigrams, there are a lot of +’s, B’s and F’s. That’s because he wasn’t perfect when tracking his masking efforts. Those are mistakes, or just the product of masking of bigrams that happened to sit next to each other, or new repeats that he wasn’t aware that he was creating.

See: http://zodiackillerciphers.com/wiki/ind … ength:_2_2

5. On a separate piece of paper, he kept a list of the two newly created bigrams, a sequence of three numbers (e.g. 6 19 36). Each time he added a wildcard, he checked above on the list to make sure that he wasn’t repeating any bigrams that he had just created in the message above. If so, then he just switched to the next wildcard on his menu. EDIT: The primary wildcard was +. When adding a + created a new repeating bigram, then he switched to the B or the F.

Hmm, this will definitely work! You came up with a way where using wildcards will destroy bigram repeats, instead of creating ones. I forgot that you can cycle wildcards, just like homophones. I think if Z was indeed using wildcards, this would be much more likely the way he did it, as it would result in lower bigram repeats we are seeing in Z340. And you can even probably check if any of the symbols that interrupt homophone cycles (i.e. they are suspected wildcards), if they form a cycle of their own?

It still leaves the issue of ambiguities in the decoded text due to too many wildcards, but Z could have been crazy enough not to care about that.

If you want to see the cipher key, message grid, and statistics, let me know. I don’t want to post it without permission because it’s not in the suite.

That’s not a problem at all. And I’ll add it to the main post, please share the cipher.

O.k.

Here is the key:

A 1 26 42 52
B 2
C 3 27
D 4 28
E 5 29 43 53 60 63
F 6
G 7 30
H 8 31 44 54
I 9 32 45 55 61
J 10
K 11
L 12 33 46
M 13
N 14 34 47 56
O 15 35 48 57 62
P 16 36
Q
R 17
S 18 38 50 58
T 19 39
U 20 40
V 21
W 22 41
X 23
Y 24
Z 25

Here is the original message, before adding wildcards to mask the bigram repeats:

16 20 17 36 12 5 8 1 25 29 26 33 46 9 14 13 24
2 17 42 32 34 12 52 19 43 33 24 39 31 45 47 7 18
4 15 56 19 38 53 60 13 39 44 63 50 1 13 5 26 3
19 55 14 6 40 34 47 24 2 20 39 61 28 35 56 19 11
14 48 22 41 54 24 58 27 40 18 29 13 43 22 8 9 46
53 32 11 45 38 50 39 31 60 58 11 24 16 20 17 36 12
63 44 42 25 5 52 33 46 1 17 57 40 34 4 28 62 47
19 11 56 15 41 55 6 61 13 3 35 13 9 14 30 20 16
48 17 4 57 22 34 26 13 32 54 42 36 16 24 62 17 45
47 13 55 18 29 17 24 41 8 52 39 43 21 53 17 61 19
9 38 39 31 1 19 7 32 17 12 36 40 39 26 50 16 60
33 46 15 56 13 63 44 5 12 36 13 29 54 43 33 16 13
53 35 8 14 48 57 31 24 60 42 44 36 20 17 16 46 63
54 52 25 5 1 12 33 45 34 13 24 29 24 43 58 28 62
47 19 11 56 15 22 55 6 61 39 18 4 26 24 35 17 14
9 30 8 19 24 48 40 21 53 7 57 39 13 60 2 46 62
41 32 34 30 2 12 15 22 45 47 7 13 24 13 55 56 28
61 38 9 19 39 35 13 48 17 17 57 41 62 17 10 20 50
19 39 31 63 5 14 4 15 6 19 32 13 29 44 43 33 36
13 53 24 60 42 54 16 40 17 36 46 63 8 52 25 5 23

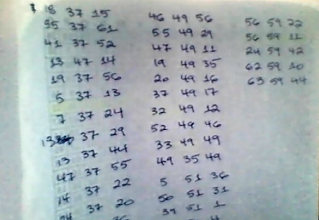
Then I performed the masking process, using 37, 49, 51 and 59 as wildcards to get the final message (the worksheet with 43 or 44 rows of three numbers each, most of which have the wildcard in the middle, is handwritten on a piece of paper):

16 20 17 36 12 5 8 1 25 29 26 33 46 9 14 13 24
2 17 42 32 49 12 52 19 43 33 24 39 31 45 47 7 18
37 15 56 19 38 53 60 13 39 44 63 50 1 13 5 26 3
19 55 14 6 40 34 47 24 2 20 39 61 28 35 56 59 11
14 37 22 41 54 24 58 27 40 18 29 13 43 22 8 9 46
53 32 11 45 38 50 51 31 60 58 11 24 37 49 17 37 12
63 44 42 25 5 52 49 46 1 37 57 40 51 4 28 62 47
19 37 56 15 41 55 37 61 13 3 35 13 37 14 30 20 16
48 17 4 57 22 34 26 13 32 54 42 36 16 24 62 17 45
47 37 55 49 29 17 24 41 37 52 39 43 21 53 17 61 19
9 38 39 51 1 19 7 32 17 12 36 40 39 26 50 16 60
33 49 49 56 13 63 44 5 51 36 13 29 54 43 51 16 13
53 35 8 14 48 57 31 24 59 42 44 36 20 49 16 46 63
54 52 25 37 1 12 33 45 34 13 37 29 24 43 58 28 37
47 49 11 56 59 22 55 6 61 39 18 4 26 24 35 17 14
9 30 8 19 24 48 40 21 37 7 57 39 13 60 2 46 62
41 32 34 30 2 12 15 22 45 51 7 13 37 13 55 56 28
61 38 9 19 49 35 49 48 51 17 57 41 62 59 10 20 50
19 39 31 63 5 14 4 15 6 19 32 13 37 44 43 33 36
13 53 37 60 42 54 16 40 37 36 46 51 8 52 37 5 23

Here is the solution:

p u r p l e h a z e a l l i n m y
b r a i n l a t e l y t h i n g s
d o n t s e e m t h e s a m e a c
t i n f u n n y b u t I d o n t k
n o w w h y s c u s e m e w h i l
e I k i s s t h e s k y p u r p l
e h a z e a l l a r o u n d d o n
t k n o w i f I m c o m i n g u p
o r d o w n a m I h a p p y o r i
n m i s e r y w h a t e v e r i t
i s t h a t g i r l p u t a s p e
l l o n m e h e l p m e h e l p m
e o h n o o h y e a h p u r p l e
h a z e a l l i n m y e y e s d o
n t k n o w i f i t s d a y o r n
i g h t y o u v e g o t m e b l o
w i n g b l o w i n g m y m i n d
i s i t t o m o r r o w o r j u s
t t h e e n d o f t i m e h e l p
m e y e a h p u r p l e h a z e x

Here are the cycle stats. It actually has more, longer, consecutive alternating two symbols cycles than the 340. But there was no random symbol selection. It started out with perfect cycles to begin with. Compare to column B.

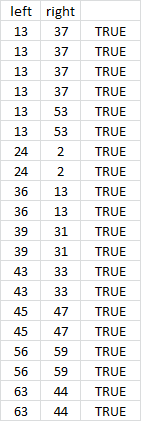
Here are the repeating bigrams before the masking process:

Here are the repeating bigrams after the masking process:

Note that I do have some repeats with wildcards 37 and 59. That happened because I wasn’t trying to be a perfectionist. I didn’t do that on purpose.

Check it out. Maybe you guys can solve it. ZKD got stalled up at about 30k for me, but you guys are a lot better at solving these things than I am. If you are interested, try the process to get a feel for what it would be like. It took me about an hour.

Smokie

Here is part of my masking worksheet:

It’s tiny but does the job. I’m not an IT guy.

Smokie

Check it out. Maybe you guys can solve it. ZKD got stalled up at about 30k for me, but you guys are a lot better at solving these things than I am. If you are interested, try the process to get a feel for what it would be like. It took me about an hour.

Yes, I can confirm that I couldn’t solve the wildcards version of this cipher. The original cipher (no wildcards) gets solved pretty easily, even though it is song lyrics, so it’s somewhat different from a normal English text, and it also has pretty rare words (haze) and a couple of contractions (actin’ and ‘scuse). But I couldn’t even see any word fragments in the wildcards version. You definitely did a really good job making it unsolvable. I also compared different stats of your cipher with Z340, and it is pretty close. You might’ve overdone the bigram repeats reduction a bit, as you only have half as many as Z340, but since Z didn’t use a computer, he could’ve simply missed many bigram repeats, or just got tired and thought it was enough.

All in all, I think this is a very plausible method of encryption that results in a cipher with very similar stats to Z340, and that can’t be solved (just like Z340). Now we need to find a way to crack it. Did you use perfect cycles when assigning wildcards? Or was it done mostly randomly? I’m just thinking if we can detect the wildcards cycling somehow?

Here’s the plaintext with the wildcards/blanks. It is still mostly readable:
PURPLEHAZEALLINMYBRAI_LATELYTHINGS_ONTSEEMTHESAMEACTINFUNNYBUTDONT_NO_WHYSCUSEMEWHILEKISSTH_SKY
PU__L_HAZEALL_RO_ND_ONTKN_WIFM_OMING_PORDOWNAMHAPPYORINMISE_Y_HATE_ERITISTHATG_RLPUTASPELLONM_
_ELPME_ELPME_HNOOHYEAHP_RPLE_AZEALL_NMYEYE_DONTK_O_IF_TSDAYORNIGHTYOUVEGOT_EBLOWINGBLOWING
MY_IN_ISITTOMO_R_W_RJUS_THEENDOFTIMEHEL_MEYEAH_URPLE_AZ_X
Wildcards do make some sections nearly impossible to discern the intended meaning, but Z might have not cared enough about that…

Interesting cipher smokie. I have included it with the main post.

There are about 50% less bigrams (period 1) in the horizontal direction than in other directions (vertical, diagonal). For higher periods (2,3,4,etc) there are then more bigrams in the horizontal direction. This does not correlate well to the 340 in a whole but does correlate highly to last 10 rows of the 340!

It’s also interesting to see how much appliance of wildcards reduce patterns found in ZKDecrypto. Like going from the 408 to the 340.

I can’t even solve your "unwildcarded" cipher with AZdecrypt, it probably suffers from the same problem as daikon3 (word entropy, same words repeating over and over again). This troubles me a bit.

Question, I see high count symbols in the normal version, are these 1:1 substitutes? If so, how many and what are the counts (this is information I like to add in the main post).

The original cipher (no wildcards) gets solved pretty easily, even though it is song lyrics, so it’s somewhat different from a normal English text, and it also has pretty rare words (haze) and a couple of contractions (actin’ and ‘scuse).

With ZKDecrypto or your own solver? I can’t seem to solve it with AZdecrypt096.

I started with symbol 37 and kept working with that for a while until trying to mask a bigram was not easy with 37. Then I switched to 49, then to 51, then to 59. The first several of each wildcard symbol is really easy. Most of it is pretty easy. I need to take a closer look at doranchak’s bigram list, but it does include several +’s, B’s and F’s. I am wondering if this is due to some kind of a flaw or lazyness in the masking process, causing some of the wildcards to be next to each other in the message. Thanks for checking this out for me.