.
Jarlve, I drafted a message this morning but the image file size was too large and I had to go to work. I think that we are basically on the same page with random shuffling of portions of a message, and I will work on that some more this weekend.
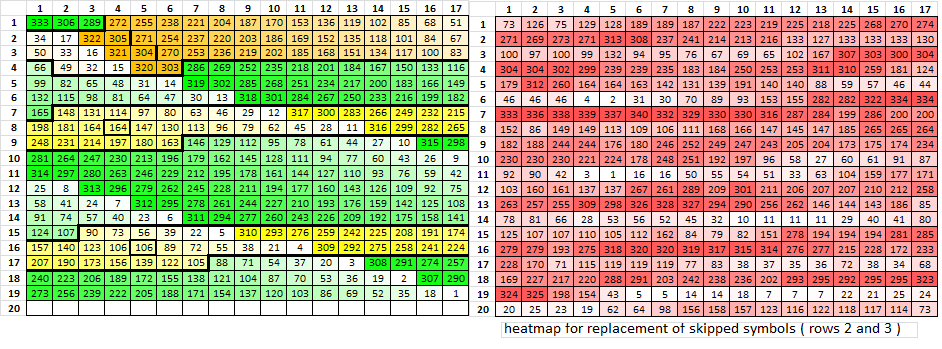
Here is the smokie14 distortion map next to the heatmaps.
The first image shows the heatmap when looking for positions where adding a skipped symbol will cause an increase in period 19 repeat counts and scores. The skipped symbols are in rows 2 and 3, and you can see that the heatmap didn’t work very well for that. The numbers in the cells are the rank of where to add a potentially skipped symbol, and adding a symbol at row 11 column 5 would cause higher period 19 repeat counts and scores.
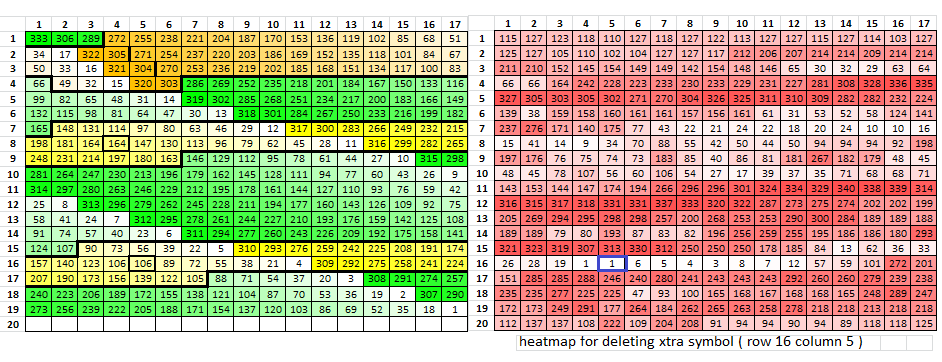
The second image shows where to delete an extra symbol. The heatmap worked perfectly in this case, because the extra symbol is at row 16 column 5.
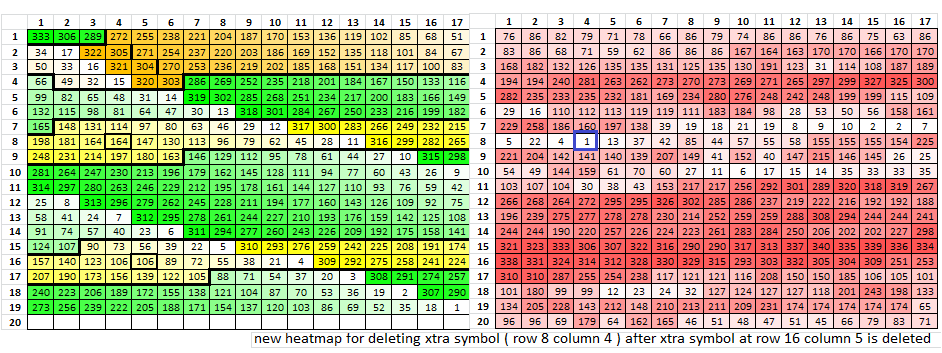
After deleting the extra symbol at row 16 column 5 and re-calculating the heatmap, it worked perfectly again because the other extra symbol is at row 8 column 4.
I don’t know how useful the heatmap is, but it was a fun exercise and gave me the idea for randomly shuffling entire rows and columns. I still haven’t tried to shuffle the columns for the 340. It looks like you put a lot of work into this exercise so far and thank you. I will work on making some constructive posts this weekend.
.
This is the candy cane wrap around Odds evens joins back to evens odds..
And this is it in flat pack.. Everything lines up period 19 scheme horizontal flip→ period 15 scheme: vertical flip bigrams, trigrams including all repeating fragments .(well everything I have checked manually) there are lots and lots..Horizontal flip → period 15 scheme: ….this is odds and evens on the bias candy cane around …also I’m not sure of the starting point..
@Mr lowe, thanks for putting it up. Your are suggesting a horizontal wrap-around offset, but what happens when the line leaves the bottom of the cipher (vertical)?
@smokie, I think your heatmaps and actual transposition matrixes are very useful. You have shown that it works for your cipher smokie14. I’m thinking of doing something in that direction. Could you possibly point or post such a transposition matrix and heatmap for a cipher (17 by 19) with one skipped symbol. Another with one added symbol. And one with a slightly different message length. I’m kinda asking allot here, if you don’t have the happen these sitting around then don’t bother creating them. I’m trying to come up with a more general approach of solving these.
Jarlve.. This is how it rotates off The bottom it comes back to the top. Your "vertical" ? I have put Purple crosses on a fragmented 19 bigram V??+?#2 , showing how it wraps back to the top . …….. I also believe the starting point is H+ M. Etcetera…… Could be wrong.. I will put up both the joined and flat packed version.. There are two sets of purple crosses. I have shown this set up as it best shows the "flow path". If doranchaks 19 bigram is the smoking gun this may help.
It’s the visual of the period 19 bigram set up..
This is the flat pack version.. Purple crosses are the fragmented bigram follow through from bottom run off back to top. I hope this answers your question jarlve..
So frustrating when it comes out horizontal instead of vertical.. Thanks in advance Doranchak… 
.
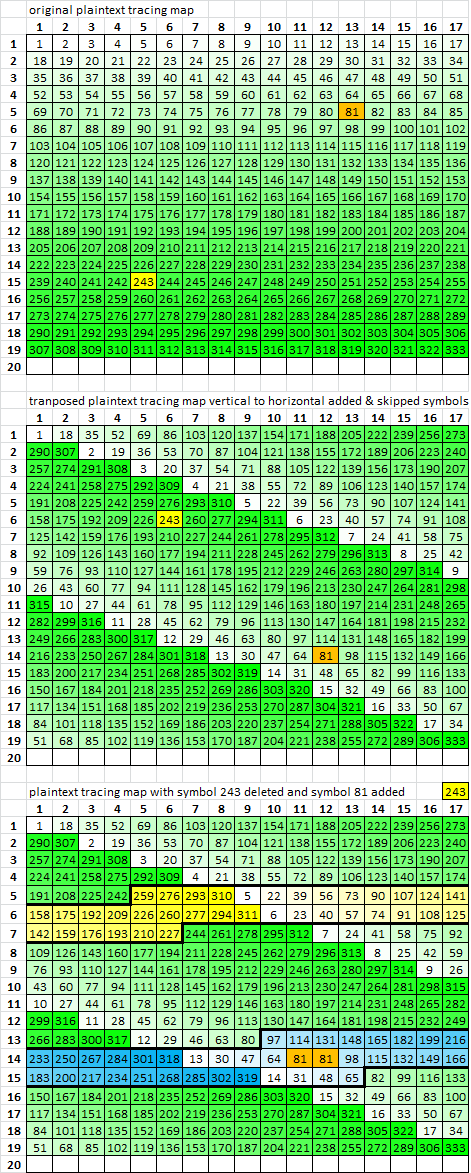
I just happen to have this lying around. It is the tracing map for smokie15, which you haven’t seen yet. The purpose for the message is basically the same as your purpose. It has one skip and one extra, but the distortion areas are separated from each other. I can make some more as well.
It is much easier for me to visualize the effect of a skipped or added symbol by thinking of the message as 340×1. The period 19 bigrams that become period 18 bigrams are those that "bracket" the position of the skipped symbol. The period 19 bigrams that become period 20 bigrams are those that "bracket" the position of the extra symbol.
When the skipped symbol is replaced or the extra symbol is deleted, they become period 19 repeats as they should be and make the period 19 repeat count and scores to be higher. "Bracketing" period bigrams with low count symbols will cause a big increase in score with a probability type scoring formula. "Bracketing" period bigrams with high count symbols will cause a small increase in score with a probability type scoring formula.
A key point is that the analysis for skipped or added symbols is the same for different types of transposition schemes. The actual message can still be thought of as 340×1.
However, there is always the possibility that some parts of the message do not have a skipped or extra symbol, but coincidentally have period 18 or period 20 bigrams with symbols that match the symbols in period 19 bigrams elsewhere in the message. This will cause a false identification if adding or deleting a symbol, causing the heatmap to make an incorrect ranking in where a symbol should be added or deleted. Sometimes the heatmap works, and sometimes it doesn’t. If memory serves me correctly, I don’t think that it worked very well with smokie15.
.
Any thoughts on this smokie..the above gives a path for doranchaks bigram 19 theory.. Starting point is on the bias wrapping around, H+M etcetera..
Any thoughts on this smokie..the above gives a path for doranchaks bigram 19 theory.. Starting point is on the bias wrapping around, H+M etcetera..
I have no idea what transposition scheme he may have used, and I don’t have the programming skills to try millions of different schemes. The only thing that I can do is try to think of explanations for why the schemes tried do not work, such as a gibberish row.
@Mr lowe, I’ve applied your latest transposition idea to the 340 (starting at H, x=1, y=1) and no solve, 37 bigram repeats. Your wrap offset works fine until position 306 (bottom right corner) so I had to improvise a little from that point.
Transposition matrix: 1 19 37 55 73 91 109 127 145 163 181 199 217 235 253 271 289 324 307 2 20 38 56 74 92 110 128 146 164 182 200 218 236 254 272 290 325 308 3 21 39 57 75 93 111 129 147 165 183 201 219 237 255 273 291 326 309 4 22 40 58 76 94 112 130 148 166 184 202 220 238 256 274 292 327 310 5 23 41 59 77 95 113 131 149 167 185 203 221 239 257 275 293 328 311 6 24 42 60 78 96 114 132 150 168 186 204 222 240 258 276 294 329 312 7 25 43 61 79 97 115 133 151 169 187 205 223 241 259 277 295 330 313 8 26 44 62 80 98 116 134 152 170 188 206 224 242 260 278 296 331 314 9 27 45 63 81 99 117 135 153 171 189 207 225 243 261 279 297 332 315 10 28 46 64 82 100 118 136 154 172 190 208 226 244 262 280 298 333 316 11 29 47 65 83 101 119 137 155 173 191 209 227 245 263 281 299 334 317 12 30 48 66 84 102 120 138 156 174 192 210 228 246 264 282 300 335 318 13 31 49 67 85 103 121 139 157 175 193 211 229 247 265 283 301 336 319 14 32 50 68 86 104 122 140 158 176 194 212 230 248 266 284 302 337 320 15 33 51 69 87 105 123 141 159 177 195 213 231 249 267 285 303 338 321 16 34 52 70 88 106 124 142 160 178 196 214 232 250 268 286 304 339 322 17 35 53 71 89 107 125 143 161 179 197 215 233 251 269 287 305 340 323 18 36 54 72 90 108 126 144 162 180 198 216 234 252 270 288 306 Resulting string: H+M8|CV@K+l#2E.B) >EB+*5k.L-RR+4>f| pMR(UVFFz9z/JNbVM )|D>#Z3P>Ldl5||.U qLFHpOGp+2|<Ut*5c ZG+kNl%WO&D(MVE5F V52+dp^D(+4(G++|T B4-R)WkVW)+k#2b^D 4ct+cW<SPYLR/5J+J YM(+|TC7zk.#Kp+fZ +B.;+c+ztZ|<z28Kj ROp+8y.LWBO1*H_Rq #2pb&RB31c_8LKJ9^ %OF7TBlXz6PYATfSM F;+B<MFG1BCOO|G)p +l2_cFKzF*K<SBK2B pzOUNyBO6N:(+H*;d y7t-cYAy29^4OFT-+ pclddG+4Ucy5C^W(c N:^j*Xz6-<Sf9pl/C
Interesting. I did my own counts, treating the added column as nulls so they don’t accidentally make new ngrams, and got 35 repeating bigrams at period 5 and 34 at period 20. The extra column might be shifting most of the period 19 bigrams to period 20. Not sure why period 5 would start peaking though (by comparison, the original 340 already has 30 bigrams at period 5).
Oops I meant period 4. The following image is a visualization of period 4 in a 18 by 20 grid. It visually correlates with the pattern but it’s still period 4. I would really like to recreate this observation, it seems significant.
The only thing that I can do is try to think of explanations for why the schemes tried do not work, such as a gibberish row.
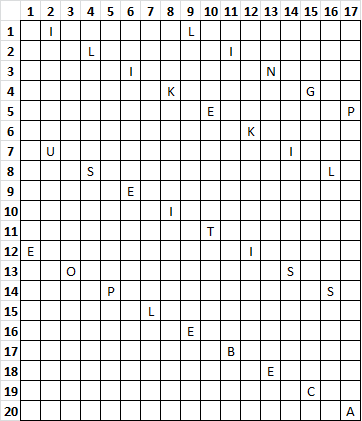
I may have found another reason. There are 20 rows in the cipher, 35 diagonal lines and 55 period 19 lines. Suppose than when transposing each time a new random period 19 line is selected. I believe this would render the cipher unsolveable with our current methods. The following image shows the starting positions for all 55 period 19 lines, note that each line is continued until you can go no further without wrapping around the cipher. Lines 1,2,54,55 only occupy one square. I’d like you to create a cipher randomly distributed over these lines.
Now I have got the full visual and workings on the period 19, I think it’s a two action transposition odds and evens and a rise of 1 per column. And what I think he did "IF period 19 is the smoking gun, is write the code out starting with odd spaces 1,3,5 etc , missing a space (even spaces) all the way through and then coming back around and continuing on filling in all the even spaces. He then gave it a column rise of 1 with wrap around from top back to bottom. Basically an interwoven odds even code with a rise of 1.
I think this explains that the even rows are 1 short in spaces per row which fits the period 19.
Can some one take doranchaks bigram 19 format, because I think that it technically gives a rise of 1 per column, and then run odds and evens separately through a solver. Not sure if that’s been done.
Not sure if anyone can understand my convoluted thought process… And it’s only a theory to the transposition if period 19 is a key. Not sure if I have got it right..cheers wishing you All success …
Can someone run odds then evens separately through a solver of the below period 19.
And thanks for looking into my theory, and being positive, jarlve doranchak and smokie.. I don’t want to hijack your good work, so let me know when it’s time to move on..
with period 19:
H+M8|CV@K+l#2E.B)
>EB+*5k.L-RR+4>f|
pMR(UVFFz9z/JNbVM
)|D>#Z3P>Ldl5||.U
qLFHpOGp+2|<Ut*5c
ZG+kNl%WO&D(MVE5F
V52+dp^D(+4(G++|T
B4-R)WkVW)+k#2b^D
4ct+cW<SPYLR/5J+J
YM(+|TC7zk.#Kp+fZ
+B.;+c+ztZ|<z28Kj
ROp+8y.LWBO1*H_Rq
#2pb&RB31c_8LKJ9^
%OF7TBlXz6PYATfSM
F;+B<MFG1BCOO|G)p
+l2_cFKzF*K<SBK2B
pzOUNyBO6N:(+H*;d
y7t-cYAy29^4OFT-+
N:^j*Xz6-<Sf9pl/C
pclddG+4Ucy5C^W(c
I may have found another reason. There are 20 rows in the cipher, 35 diagonal lines and 55 period 19 lines. Suppose than when transposing each time a new random period 19 line is selected. I believe this would render the cipher unsolveable with our current methods. The following image shows the starting positions for all 55 period 19 lines, note that each line is continued until you can go no further without wrapping around the cipher. Lines 1,2,54,55 only occupy one square. I’d like you to create a cipher randomly distributed over these lines.
I was thinking something very similar last night. You must be reading my mind. What you are saying is that one way to create a very difficult transposition cipher is to lift plaintext from a message working from left to right, top to bottom. And placing the plaintext into period 19 diagonal rows, selecting the rows at random. And doing that until the message grid is full. Is that correct?
Last night I was wondering if the solver programs need to work with a 17×20 or similar grid. I was thinking about un-transposing all of the individual period 19 diagonal rows into horizontal rows. They would range in length and somehow connect to each other in an unknown way. But align those un-transpositions into horizontal rows and then fill in the same null at the end of each row so that all of the rows are the same length. Then try to solve. Either that or modify the solver to score strings of period 19 diagonal rows instead of period 1 horizontal rows. If we can do something similar to that, then we can figure out how he transposed the message after getting a rough solution.
I came up with 36 diagonal rows at -45 degrees. But verify my question above and then I will start on a message or draw something up to make sure that we are understanding each other. It will be a bit of work so I want to make sure we are talking the same thing first. I already have a perfect plaintext message ready to go and it is not one you are familiar with.
I have my results from smokie16a-d row shuffle experiment, which I will post soon. But I am excited about your new idea.
.
.
Like this, right?
EDIT: Do you want a message that you are familiar with, or one that is new? Maybe starting with one you are familiar with would be better so that you can more easily see if your efforts are working.
.
I was thinking something very similar last night. You must be reading my mind. What you are saying is that one way to create a very difficult transposition cipher is to lift plaintext from a message working from left to right, top to bottom. And placing the plaintext into period 19 diagonal rows, selecting the rows at random. And doing that until the message grid is full. Is that correct?
Yes that’s correct. And like in the image I just see you posted now. There are 55 lines as the image from my previous post depicts. I think that most period 19 interpretations we have explored basicly come down to various reading rules of these 55 lines. If I could solve your message somehow and not the 340 then we could somewhat rule out a bunch of clean transposition schemes (that are proper rearrangements of these 55 lines).
Update: prefer new message.
Last night I was wondering if the solver programs need to work with a 17×20 or similar grid. I was thinking about un-transposing all of the individual period 19 diagonal rows into horizontal rows. They would range in length and somehow connect to each other in an unknown way. But align those un-transpositions into horizontal rows and then fill in the same null at the end of each row so that all of the rows are the same length. Then try to solve. Either that or modify the solver to score strings of period 19 diagonal rows instead of period 1 horizontal rows. If we can do something similar to that, then we can figure out how he transposed the message after getting a rough solution.
My program just sees the cipher as a straight line but remembers the dimensions of the input cipher. Yes, un-transpose and then rearrange the period 19 lines. If you fill in nulls then the solver may not have enough information to work with but I get your idea. Another idea is to only work with the longer lines or build n-grams from similar samples. I will consider these if need be.
I have my results from smokie16a-d row shuffle experiment, which I will post soon. But I am excited about your new idea.
Yeah me too.
