Another strange observation but I’m not sure what to make of it.
I have now also included transposed period bigram (c*(c-1)) analysis in my routine and the results seem strange. The upper graphs are normal untransposed periods and the lower graphs are transposed periods. I noticed that there seemed to be some alternating thing going on, one graph higher, one graph lower. The images are a bit large so I just made them to click.
So I thought that perhaps the "+" symbol could be causing this and replaced its instances with new symbols raising the symbol count to 86. It made it worse. What are we seeing here in the lower graphs? The first 20 periods seem to have a period of their own going on. It’s possible that I’m not understanding things correctly. Though I’ve not been able to reproduce it, my current best guess is that it may be related to the encoding somehow (here we go again).
Is this a real phenomena?
I am having trouble understanding your steps. First, can you explain what your c*(c-1) analysis is? Is "c" the number of repeated bigrams and you are multiplying it by "c-1"?
The first image has two graphs. The first graph represents periodic bigram counts for the unaltered 340, right? For the second graph, what do you mean by "transposed periods"?
What exactly gets "worse" in the 2nd image? Do you mean that the appearance of seemingly regular intervals becomes more apparent?
Yes, if a bigram is repeated 3 times then it scores 3*2=6.
The first graph represents periodic bigram counts for the unaltered 340, right?
Yes.
Untranspose period 2: 123456789 becomes 135792468.
Transpose period 2: 123456789 becomes 162738495.
It’s probably nothing (a bigram discrepancy between odds and evens blown up perhaps) but on the other hand it’s interesting to experiment with new things you normally wouldn’t do. I learned that doing a period 19 transposition on a plaintext then followed by a period 18 transposition will actually solve the cipher almost perfectly. I wouldn’t have thought of that.
What we think is a period 19 transposition may be a period 18 untransposition or a period 15 transposition may be a period 23 untransposition. ![]()
Yes, if a bigram is repeated 3 times then it scores 3*2=6.
AB AB AB AB <== do you count this as 3 repeats or 4?
Transpose period 2: 123456789 becomes 162738495.
Oh, ok, I think I understand. If I’m not mistaken, for your given example string, "transpose period 2" is equivalent to "untranspose period 5", at least in the way that I’ve been doing them.
So… that suggests that the inverse of a transposition operation is equivalent to some other transposition operation. I think.
Another way to look at it: Let T(n,c) = transposition of cipher c at period n. Let T'(n,c) = inverse of transposition of cipher c at period n. So you can say this: T'(n,T(n,c)) = c. (Applying the transposition and its inverse gives you back the original cipher text).
Then, I think for a given n, there is some m such that T(m,c) = T'(n,c). Maybe? I’m suspecting that m might be determined by the cipher length divided by n.
I think I hurt my brain. ![]()
AB AB AB AB <== do you count this as 3 repeats or 4?
3 repeats, so it ends up being a 6.
Yes, it has to do with the length of the message and if the period is a factor of it. A period 20 transposition on a 340 character plaintext followed by a period 17 transposition will perfectly undo it. But stacking period 19 and 18 transposition will cause some errors on a regular period:
ilikekillingpeopl ybecauseitissomuc heunitismorefunth anfillingwildgame intkeforrestbecau semahisthemostdan gerounanimalofall tokillsomethinggi vesmethsmostthril lingexpeeenceitis evenbetterthanget tingyourrorksoffw ithagirlthecestpa rtofitisthatbheni dieiwillberebwrni nparadiceandaloth eihavekilledwillb ecomemyslavesiwil lnotgiveyoumyname lbecauseyouwilltr
I really think it is somewhat interesting because it seems to uncover more unusual stuff with the 340 bigram statistics. The following bigram graphs are for the mirrored 340. Notice that there is a secondary peak at 54 for the transposed periods. There’s allot of strange things going on with the bigram statistics that doesn’t seem to correlate with regular period 15, 19 schemes. I’m starting to believe that we have missed something and it probably is nothing like a simple misalignment. Also remember period 5 repeats when 18 by 20.

And here is a period 15 transposition for the 408 (340 character part).

Here’s a package that contains the periodic bigram visuals from 1 to 19 for the p1 plaintext (340 char 408): https://drive.google.com/open?id=0B5r0r … XkxTkhiYUE
You can then use your image browser to slide through to get a feel for what happens with the graphs at various periods, quite cool!
Edit: https://www.youtube.com/watch?v=1AirYqW … e=youtu.be
Jarlvie and smokie. I made up a physical scytale for COLUMNS today spreadsheet numbers all colored period 19s. I will check it with the first one I made a few weeks back later on.. I noticed that the(row 19 periods) when looked at in a column format is @ period 21 coming together in the vertical but also (always?) its related color is picked up at period 11 in the horizontal as it goes past.
Still here and watching. Feeling better but have been stuck in first gear for a few days. Having a few spreadsheet issues and hope to resolve.
EDIT:
Period 19 scytale cipher with one null symbol inserted after transposition:
Jarlve, I will work on your message soon now that I have my spreadsheet issues almost resolved. You mean that you added one symbol as a null in multiple places to create multiple misalignments, right? Just checking.
hi smokie ..good to hear your on the improve.. don’t forget that if you put a last row of nulls(junk) into a skytale they will be dispersed throughout the code.
Jarlve, I will work on your message soon now that I have my spreadsheet issues almost resolved. You mean that you added one symbol as a null in multiple places to create multiple misalignments, right? Just checking.
Yes, as I thought you asked. But if you want something else entirely let me know.
Jarlve, I will work on your message soon now that I have my spreadsheet issues almost resolved. You mean that you added one symbol as a null in multiple places to create multiple misalignments, right? Just checking.
Yes, as I thought you asked. But if you want something else entirely let me know.
That is what I wanted. Thanks.
EDIT: I have been thinking about the method of construction. You don’t need a long strip of paper or cloth. All you have to do is tape an 8-1/2" x 11" piece of paper to a cylinder. Write the message vertically down the length of the paper so that there are 19 columns on the paper. Then un-tape and you have a transposition cipher already written on a piece of paper.
Mr. Lowe, my suggestion is that you try this. First make one with the "I like killing" message and do it perfectly with no mistakes. Describe what it is like to do that. I may also do it myself because I want to know what it is like.
EDIT 2: Never mind. I tried it and realized after drafting one column that it is not necessary to wrap a piece of paper around a cylinder to write a message vertically so that there are 19 columns.
12?
@smokie,
Correct, was it easy or hard? Do you think any symbol in the 340 is worth looking at in that manner?
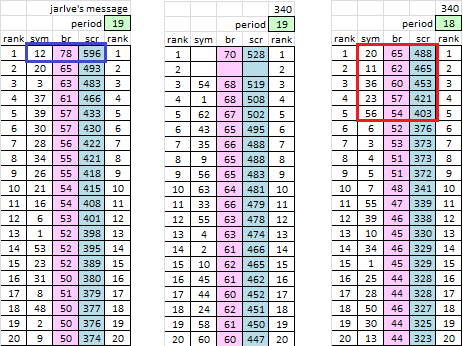
It was very easy. I didn’t use the heatmap, but just deleted all of symbol x from 1 to 54 and counted and scored the period 19 matches. See the results ( left ), where symbol 12 had a * much * higher response than the other symbols.
I did the same thing with the 340 period 19 ( center ), and no symbol had a similar response; deleting symbol x from 1 to 63 resulted in lower scores in every case.
However, I did the same thing with the 340 period 18 ( right ), and found that although the scores are not quite as high, deleting symbol 20, the B, had the highest response. I found that interesting because the B is not cyclic. Other high count symbols, such as 11, 36 and 23, caused higher responses. Maybe that is no big deal because we already know about the period 19 repeats, and these results may be expected.
Perhaps deleting some combination of the period 18 high response symbols, converting the 340 to a period 18 transposition, is worth looking at.
I think that it is also a good idea to explore adding or deleting a symbol at every nth position starting at position x. That would help to flush out cyclic misalignments, if there are any.
I got a partial solve, but not perfect.
Score: 26848 Ioc: 626 M: 377 C: 342 S: 129 bytheworldofflativ eyearingtheartofac cusescanbedistingo verclasseshavemove rsignthevoiceofall ofthelowerclassedp ropersonbyfeelingi nguishedbytheartho ughtrecognitioncom plestoicebutthelin gasenablingthemtha theelingpractisedt obeconfigurational inclassesaredistru ckingandtheartofro mthedbythesoundoft hevelopedtocalorad ingonorevenacircha ndwomendeterminedw