From here: https://docs.google.com/spreadsheets/d/ … sp=sharing

Z340 (Symbolic):

HER>pl^VPk|1LTG2d
Np+B(#O%DWY.<*Kf)
By:cM+UZGW()L#zHJ
Spp7^l8*V3pO++RK2
_9M+ztjd|5FP+&4k/
p8R^FlO-*dCkF>2D(
#5+Kq%;2UcXGV.zL|
(G2Jfj#O+_NYz+@L9
d<M+b+ZR2FBcyA64K
-zlUV+^J+Op7<FBy-
U+R/5tE|DYBpbTMKO
2<clRJ|*5T4M.+&BF
z69Sy#+N|5FBc(;8R
lGFN^f524b.cV4t++
yBX1*:49CE>VUZ5-+
|c.3zBK(Op^.fMqG2
RcT+L16C<+FlWB|)L
++)WCzWcPOSHT/()p
|FkdW<7tB_YOB*-Cc
>MDHNpkSzZO8A|K;+

Z340 (Numeric):

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
18 5 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
20 34 35 36 37 19 38 39 15 26 21 33 13 22 40 1 41
42 5 5 43 7 6 44 30 8 45 5 23 19 19 3 31 16
46 47 37 19 40 48 49 17 11 50 51 9 19 52 53 10 54
5 44 3 7 51 6 23 55 30 17 56 10 51 4 16 25 21
22 50 19 31 57 24 58 16 38 36 59 15 8 28 40 13 11
21 15 16 41 32 49 22 23 19 46 18 27 40 19 60 13 47
17 29 37 19 61 19 39 3 16 51 20 36 34 62 63 53 31
55 40 6 38 8 19 7 41 19 23 5 43 29 51 20 34 55
38 19 3 54 50 48 2 11 25 27 20 5 61 14 37 31 23
16 29 36 6 3 41 11 30 50 14 53 37 28 19 52 20 51
40 63 47 42 34 22 19 18 11 50 51 20 36 21 58 44 3
6 15 51 18 7 32 50 16 53 61 28 36 8 53 48 19 19
34 20 59 12 30 35 53 47 56 2 4 8 38 39 50 55 19
11 36 28 45 40 20 31 21 23 5 7 28 32 37 57 15 16
3 36 14 19 13 12 63 56 29 19 51 6 26 20 11 33 13
19 19 33 26 56 40 26 36 9 23 42 1 14 54 21 33 5
11 51 10 17 26 29 43 48 20 46 27 23 20 30 55 56 36
4 37 25 1 18 5 10 42 40 39 23 44 62 11 31 58 19

Here’s an example of a symbol relationship the cosine similarity measurement detects in the flip-period15-periodRow10 scheme:

The "G" and backwards "p" are strongly associated because they are preceded by, and followed by, some of the same sets of symbols:

Notice how the occurrences of G and backwards P are preceded by:
– triangle symbol
– top half filled circle
– backwards D
– O
– +
– vertical bar

And how they are followed by:
– +
– bottom half filled circle

If they stand for the same plaintext letter, then that could explain why they share symbols in this way since they are behaving as the same letter.

Another example involving phi (circle with vertical bar) and theta (circle with horizontal bar):

Notices how the occurrences of phi and theta are preceded by:
– W
– M
– R

And how they are followed by:
– +

doranchak .. what happens to the pivot constructions when you do this process.. can you highlight the pivots first and repeat the above process to see if they have any relationship with your above workings.

I’m going through the thread, ouch, there’s allot. Hold on.

Do you recall who on this forum was the first one to notice the period 15/19 phenomenon? I think it is a very important discovery and whoever found it should be acknowledged.

I was aware of it since early 2015, after writing my first version of Examine (my stats and interactive solving program). I first mentioned it in the thread "Schemes 340": viewtopic.php?f=81&t=2158&hilit=schemes&start=20

Another question is, which has probably been discussed before, why are there so few patterns in the 340 versus the 408? If not subtly transposed after encoding it does hint towards some randomization of the plaintext.

I’ve looked at bigrams at a distance for the 340 and found some unusual peaks (for my system) at distances of 15, 19 and 29. A distance of one would be a standard bigram, I’m not sure if it’s something or just a fluke in the cipher. It could be related to the "+" symbol only landing on a prime number just once. The 340 is trouble, and the way the cipher is throws of many tests, I have wondered if he was really that smart. Let’s hope not!

I like the scatter-graph. There are some points that are much higher than the cluster, and they seem roughly evenly spaced forming a horizontal line just under 2100. They score high, even though they may have fewer repeats. Did you check into those more closely?

Yes, I revisited them just now and I think they are caused by the shortening of the cipher text by certain transposition operations. I believe I made the plot before I realized that i needed to normalize the azdecrypt score based on cipher length, because it is higher for shorter ciphers.

AZdecrypt already normalizes by cipher length. It’s just that with shortening of the cipher the multiplicity increases and more sensible stuff can be made to fit. The latest versions of AZdecrypt have the option to add multiplicity normalization, after some experiments a value of 1.3 here seems to be really good approximation for the 340.

Another observation that I do not know exactly how to explain. When I make transposed messages, usually some of the highest counts of period x repeats are still period 1 to about period 5.

This is from the encoding, cyclic encoding has a higher chance to preserve bigrams than random encoding. At periods 1 to 5, the order of the encoding is still very actual but at higher periods the returns diminish. I don’t have any hard numbers to back this up, it’s just what I’ve seen from creating so many ciphers.

EDIT: not sure if I interpreted this correctly.

And here is a graph of the stats. The x-axis is the period, except that it only shows period 20, 40, 60, etc. The blue line shows the transposed stats, and the red line shows the untransposed stats. Notice that on the left portion of the graph, the shapes of the lines are very similar but exaggerated for the untransposed. On the the right side of the graph, the lines are not so similar and the untransposed numbers do not follow the transposed numbers.

This seems most promising smokie, can we see the results for the 340?

So I ran a quick experiment combining the different measurements: 1) repeating bigrams, 2) fragment ioc (my custom measurement of repeating fragments), 3) comparison of cosine similarity distribution against shuffled Z340. The idea is to see if the different measurements confirm each other when a true untransposition is found. I didn’t find a true transposition but the "best" one found during the search was this:

FlipHorizontal() Period(15) PeriodRow(10) (Interpretation: Mirror the Z340 horizontally, then untranspose at period 15, and then read out the rows with period 10 — that is, print out row 1, then row 11, then row 2, then row 12, etc.)

It’s strange how some things keep coming back! The PeriodRow(10) seems suggestive of Dan Olson’s theory, yet after mirroring and period 15 transposition!

AZdecrypt 0.992 (Practical Cryptography 5-grams) External, Index of coincidence

Score: 23902.14 Ioc: 0.06413326 Entropy: 4.114048 Chi-square: 57.28067 Characters: 340 Letters: 22

ferengirulesofacq
uisitiononceyouha
vetheirmaneynever
giveitbacwneverpa
ymoreforanacquisi
tionthanyouhaveto
neverallarfamilyt
ostandinthewayofo
pportunityamaniso
nlyrarththesumofh
ispossessionsweep
yourearsopensmall
printleadstalarge
risropportunitypl
usinstinctequalsp
rofitgreedisetern
alanythingworthdo
ingisrarthdoingfo
rmoneyadealisadea
luntilabetteronec

Multiplicity: 0.1882353 Characters: 340 Symbols: 64

Jarlvie was the above one of your test ciphers

doranchak .. what happens to the pivot constructions when you do this process.. can you highlight the pivots first and repeat the above process to see if they have any relationship with your above workings.

Sure –

Z340 flipped horizontally:

Then applying Period 15:

Then applying Period Row 10:

FlipHorizontal() Period(15) PeriodRow(10) (Interpretation: Mirror the Z340 horizontally, then untranspose at period 15, and then read out the rows with period 10 — that is, print out row 1, then row 11, then row 2, then row 12, etc.)

Another high-scoring transposition found by the search was:

PeriodColumn(2) Period(18) PeriodRow(15) (interpretation: Re-arrange columns at period 2, then apply period 18, then re-arrange rows at period 10.)

H+M8|CV@Kz/JNbVM)
+B.;+B31c_81*H_Rq
|DR(UVFFz9<Ut*5cZ
#2pb&RG1BCOO|TfSM
G+kNpOGp+2|G++|TB
F;+B<MF6N:(+H*;2B
4-R)Wk^D(+4(5J+JY
pzOUNyBO<Sf9pl/CN
M(+|TC7zPYLR/8KjR
:^j*Xz6-+l#2E.B)>
Op+8y.LWBO|<z29^%
OF7TBlXz6PYALKJp+
l2_cFKzF*K<SBKG)y
7t-cYAy29^4OFT-+d
pclddG+4Ucy5C^W(c
MEB+*5k.L-RR+4>f|
pFH>#Z3P>Ldl5||.U
qL+dpl%WO&D(MVE5F
V52cW<SVW)+k#2b^D
4ct+c+ztZk.#Kp+fZ

I think these schemes have come up before in my experiments.

I feel like we are close, and that the set of operations is simply too limited to include whatever missing operation(s) there might be. One thing is for sure – I have not attempted to measure all the different ways that columnar transposition could have been applied (regular or irregular). My set of operations do not yet include all the possible column re-orderings that need to be examined.

Or perhaps you guys were on the right track before with the wildcard or misalignment hypothesis. That pesky over-abundant plus symbol still nags at me.

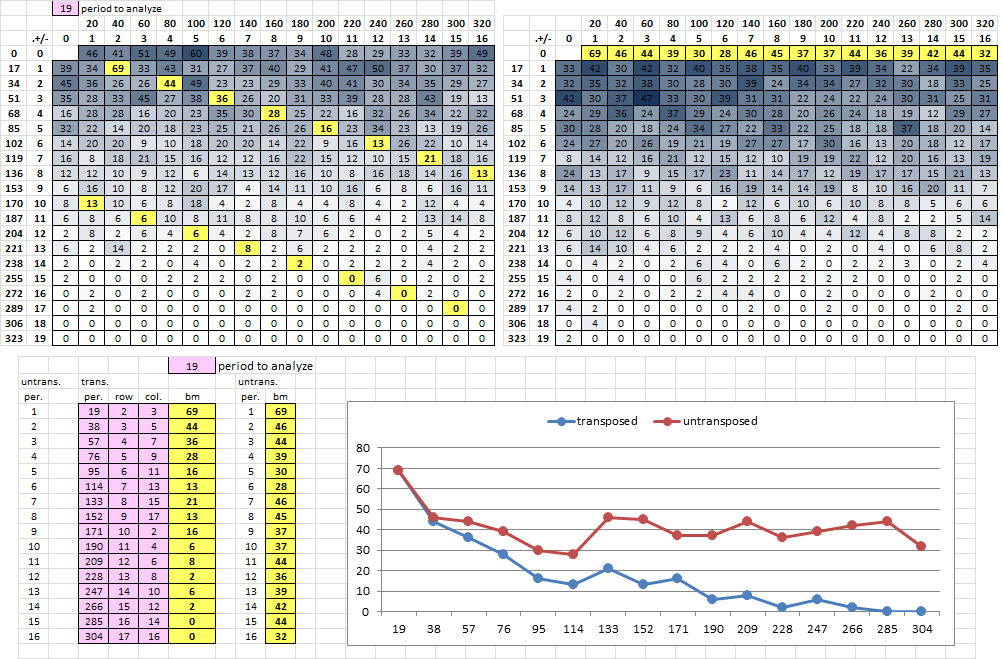
I am not sure how promising it is. I revised my all period spreadsheet so that I can change the period to whatever I want without having to change formulas or formatting in a lot of different cells.

Here is the untransposed 340 at period 19 by re-drafting at 19 columns wide to line up the repeat symbols vertically, then rotating 90 degrees, then re-drafting again to 17 x 20. The lines are similar, but I don’t have any interpretation to offer. The above experiments two weeks ago had some spreadsheet issues.

I have been thinking about ways to compare two graph lines for similarity, and for me something simple is more appropriate. I may just wind up comparing the sums of the line segments. I was thinking about performing some tests of untransposed correctly versus untransposed incorrectly for comparison. It may work and it may not.’

I got the idea when highlighting the repeats cells, currently yellow below. On the left is the 340, and on the right untransposed as described above.

I was making messages a few weeks ago and wanting to see how far down the values show up in the highlighted cells. For instance, on row 13 in the table below left, there is a value of 8 in one of the repeat cells, and it is higher than all of the other cells in that row ( except for the value 14 ). So there is a lot of randomness involved to compare with and I was trying to think of a way to eliminate some of the randomness and narrow down different untransposition schemes as the most probable.

The messages that I made generally show higher values in the lower repeat cells as compared to cells in the same row. Currently working in small steps when I can.

He was smart. If the message didn’t have 63 symbols, then we would probably be able to recognize when we had the correct untransposition. The problem is that homophonic substitution makes recognizing the correct untransposition very difficult. And transposition makes solving impossible unless transposition is detected. You did that.

I still think that the high count non cyclic symbols, especially the +, B and q, are polyalphabetic. I think that they can be expanded into multiple symbols that will each cycle with other symbol groups. Perhaps the cycle scheme causes prime phobia. I am just putting this out there, whether right or wrong. I am saying that even if we did know how to untranspose it correctly, we wouldn’t be able to recognize it because of polyalphabetic symbols. And so we don’t know what untransposition to focus on. You may have already untransposed it correctly and didn’t know it. And maybe there are skips or nulls, not to ignore some of the other strange phenomena.

I was able to solve your last transposition message from six or seven weeks ago very easily by reconnecting the repeat symbols. At least good enough to recognize a true message because there were a lot of words that had context with each other. It was some sort of science fiction space exploration / human expansion into other solar systems theme. Something like that. Context is really important, and think that looking for multiple words from Zodiac’s known vocabulary from untransposed messages with expanded symbols is the way to go. An extra bonus Zodiac score, so to speak. Perhaps include newspaper articles about Zodiac in the context dictionary. I am not asking anybody to do it, just putting it out there for people to think about some time in the future.

I burn out and get refreshed from time to time. Factors include frustration after putting a lot of effort into one particular idea, and other areas of my life. If there is a 1st gear, 2nd gear, 3rd gear, 4th gear and overdrive, I am in 1st gear right now because I have to be. I have to change gears when necessary so I don’t blow out my transmission. I will mess around with the graph lines some more in a while.

AZdecrypt 0.992 (Practical Cryptography 5-grams) External, Index of coincidence

Score: 23902.14 Ioc: 0.06413326 Entropy: 4.114048 Chi-square: 57.28067 Characters: 340 Letters: 22

ferengirulesofacq
uisitiononceyouha
vetheirmaneynever
giveitbacwneverpa
ymoreforanacquisi
tionthanyouhaveto
neverallarfamilyt
ostandinthewayofo
pportunityamaniso
nlyrarththesumofh
ispossessionsweep
yourearsopensmall
printleadstalarge
risropportunitypl
usinstinctequalsp
rofitgreedisetern
alanythingworthdo
ingisrarthdoingfo
rmoneyadealisadea
luntilabetteronec

Multiplicity: 0.1882353 Characters: 340 Symbols: 64

Jarlvie was the above one of your test ciphers

That is plaintext p100. I don’t know/remember if it was a cipher by me.

Or perhaps you guys were on the right track before with the wildcard or misalignment hypothesis. That pesky over-abundant plus symbol still nags at me.

One of the things I’m currently doing is looking at the 340 as it just being a wildcard cipher (again). It was daikon who at the time cracked smokie’s purple haze cipher (a hard cipher just by its own) and then applied the same attack to the 340 which gave nothing (trying limited sets of high count symbols as wildcards). I’m using a more thorough approach to provide a more definite answer.

But perhaps transposition + wildcards?

I still think that the high count non cyclic symbols, especially the +, B and q, are polyalphabetic. I think that they can be expanded into multiple symbols that will each cycle with other symbol groups. Perhaps the cycle scheme causes prime phobia. I am just putting this out there, whether right or wrong. I am saying that even if we did know how to untranspose it correctly, we wouldn’t be able to recognize it because of polyalphabetic symbols. And so we don’t know what untransposition to focus on. You may have already untransposed it correctly and didn’t know it.

I’m taking another look at wildcards right now so maybe that work could be expanded into wildcards + transposition, no promises though.

I also wonder if these wildcard symbols are then the cause of the disrupted cycles. And if we can fashion together some sort of test for this. That could prove a big step forward.