I have a lot of irons in the fire with this project.
Another one is to try to find a cipher other than route transposition that would cause period 15/19 repeats. Daikon discussed bifid briefly and questioned why the period would be 38. I have been trying to figure out how a bifid ciopher causes period x/2 repeats. Perhaps I should add to my list making a message with period 30 , and then transcribe right left top bottom to see what would happen. To see if I can use bifid to create a message that has as many period 15/19 repeats as the 340. I understand how the cipher works, but not how the period repeats are created. Maybe doing it will help me understand.
Still working on tw1, expanded 4, 5, 14, 19 and 47 and untransposed period 14 transcription left right top bottom and right left bottom top. A lot of variance and no solve.
Created a bifid cipher with http://rumkin.com/tools/cipher/bifid.php and repeats peaked at period 170 (340/2), the website states "The Bifid cipher is considered a more secure cipher because it breaks the message apart into two separate streams and then recombines them." seems to be true.
After that I undid row period 10 and found that this divided the period by 10, so the period 170 repeats became clean period 17 repeats. Semi interesting because doranchak has some high scoring results with this operation (row period). It is also interesting that it does not seem to produce "reflections" at multiples of the period (which is an indication of plaintext transposition).
Here is such a cipher, to be clear, transposition + wildcards. Could be any of these: (period, skytale, diagonal, non-keyed regular and irregular columnar transposition) and anywhere between 3 to 6 wildcards. ** Oh, and one extra step somewhere, be either flipping, mirroring or reversing the cipher. ** Didn’t try-hard to emulate the 340. Should prove difficult but I hope you guys could take a look at it.
About jarlve_tw1. It’s a very hard cipher, you may just want to take a look at it and not much more. ![]()
I have a lot of irons in the fire with this project.
Another one is to try to find a cipher other than route transposition that would cause period 15/19 repeats. Daikon discussed bifid briefly and questioned why the period would be 38. I have been trying to figure out how a bifid ciopher causes period x/2 repeats. Perhaps I should add to my list making a message with period 30 , and then transcribe right left top bottom to see what would happen. To see if I can use bifid to create a message that has as many period 15/19 repeats as the 340. I understand how the cipher works, but not how the period repeats are created. Maybe doing it will help me understand.
Still working on tw1, expanded 4, 5, 14, 19 and 47 and untransposed period 14 transcription left right top bottom and right left bottom top. A lot of variance and no solve.
Created a bifid cipher with http://rumkin.com/tools/cipher/bifid.php and repeats peaked at period 170 (340/2), the website states "The Bifid cipher is considered a more secure cipher because it breaks the message apart into two separate streams and then recombines them." seems to be true.
After that I undid row period 10 and found that this divided the period by 10, so the period 170 repeats became clean period 17 repeats. Semi interesting because doranchak has some high scoring results with this operation (row period). It is also interesting that it does not seem to produce "reflections" at multiples of the period (which is an indication of plaintext transposition).
The bifid message creator at that site must have had a period of 340, the length of your message. Other descriptions of bifid use a much smaller period, such as 5. I am interested in trying to make a message with bifid and emulating 340 stats, to see if I can and how easy or difficult it would be. When I made the message that had high period 19 repeat counts but was not a transposition message, I learned that one very important statistical fact about the 340 is the low count of period 1 repeats as compared to period 19 repeats. That was difficult to reproduce with a straightforward homophonic cipher.
Take a look at Practical Cryptography’s explanation of Bifid:
http://practicalcryptography.com/ciphers/bifid-cipher/
http://practicalcryptography.com/crypta … id-cipher/
The site’s use of the word "period" is confusing when trying to read the explanation and cryptanalysis pages together. But I sort of get that even numbered periods are easier to identify than odd numbered periods. Looking at the distribution of bigram counts on the cryptanalysis page reminds me of the period 29/30 or period 38/39 issue.
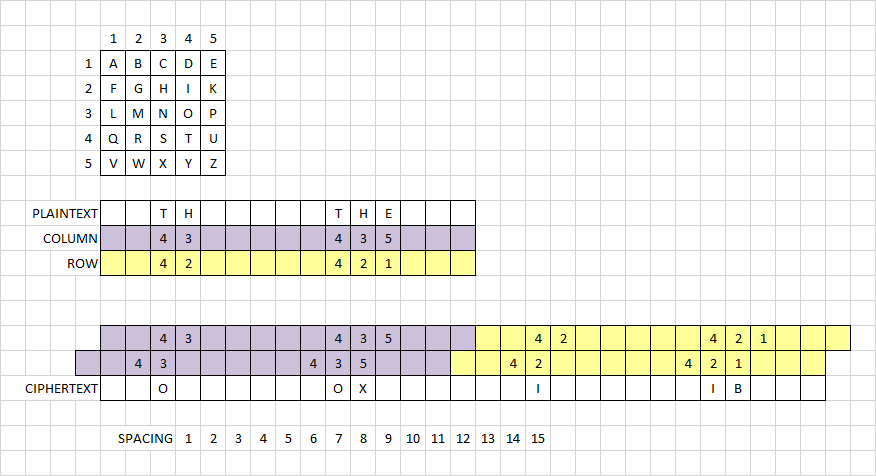
I made a little bifid message to see how period x repeats are created, and indeed the cipher does just that.
My message is 15 plaintext long, except that I left out most of the plaintext for clarity. I included only the digraph TH and trigraph THE. The Polybius square is at the top. Then the message, with the TH and the THE. The purple cells have the column number and the yellow cells have the row number. Then at the bottom it might seem a bit confusing. But with bifid, you take the bottom ROW numbers and move them up to follow the COLUMN numbers. That would be yellow next to purple.
There is another yellow next to purple just below that, which is not exactly how other examples of bifid are shown but do the same thing. It shows that you take two adjacent COLUMN or ROW values and convert them into a COLUMN ROW value and find the ciphertext in the Polybius square. For example, the first T is COLUMN 4 ROW 4, and the first H is COLUMN 3 ROW 2. Take the COLUMN 4 from the T and the COLUMN 3 from the H and use those to make a new ciphertext, O.
In any case, TH at period 1 becomes OI at period 15. HE at period 1 becomes XB at period 15. High frequency plaintext digraphs are going to show up as high frequency period x repeats in the ciphertext, where x = length of message chunks moved around.
The O and the X are next to each other and the I and the B are next to each other. It seems to me that you wouldn’t get the characteristic diagonal rows of repeat symbols, as with the 340. Instead, I think that the repeats would show up in horizontal clusters. It would be fun and easy to test that, and I may this weekend. I think that a comparison of period 30 repeat scores for a 15 row route transposition compared to period 2 repeat scores for a period 15 bifid may help explain things.
If anyone knows of any other cipher type that creates period x repeats, please let me know.
smokie can you recall if it was your "smokie27" that solves.. ferengi rules of acquisition once you .. if not yours was it jarlves?
I was going through some of the test ciphers and found one Jarlve made that has very high multiplicity (the ratio of unique symbols to cipher length is very high). I ran it through a basic azdecrypt run and the word "ferengi" appeared:
ismfallysingingha
mirofttothattothc
ondoutoclostalkin
ghistofoundproain
nahwhichanbatchon
thawhichitaltered
edineperedeserien
cereseresevewhene
vereddedtheleveme
mbelletewererever
evereveredoesease
recomeresenewerer
eseseveredagestri
ciergenessenthert
iesideferenginfac
ticestointeratesl
owellencecomewash
inityformededhesp
ellioninandthever
belocatedandherew
erenotewemusevene
wwerofthepledinat
edthesewherealtak
ethernatheringthe
rterestedstatesme
reviestherevertic
leweredanddes
I think he made the cipher to mimic the still-unsolved "alanbenjy" cipher which also has high multiplicity.
Here’s Jarlve’s post with the cipher: viewtopic.php?p=42645#p42645
I was going through some of the test ciphers and found one Jarlve made that has very high multiplicity (the ratio of unique symbols to cipher length is very high). I ran it through a basic azdecrypt run and the word "ferengi" appeared:
I think he made the cipher to mimic the still-unsolved "alanbenjy" cipher which also has high multiplicity.
Here’s Jarlve’s post with the cipher: viewtopic.php?p=42645#p42645
That’s almost hilarious to me. Because Ferengi is certainly not a part of that plaintext but they do (the Ferengi) have a knack of popping up everywhere in the Star Trek universe! It’s perhaps kinda amazing that you spotted that doranchak.
The bifid message creator at that site must have had a period of 340, the length of your message. Other descriptions of bifid use a much smaller period, such as 5. I am interested in trying to make a message with bifid and emulating 340 stats, to see if I can and how easy or difficult it would be. When I made the message that had high period 19 repeat counts but was not a transposition message, I learned that one very important statistical fact about the 340 is the low count of period 1 repeats as compared to period 19 repeats. That was difficult to reproduce with a straightforward homophonic cipher.
Ok smokie, looking forward to your examination. I just look a bit at it and think it is unlikely that the 340 = bifid.
Based on those stats, the unmanipulated Z340 already produces an azdecrypt score at a statistical significance level of 2.7 sigma (2.7 times one standard deviation) compared to the 10,000 random shuffles.
It’s something that still bothers me. I wonder if it is the encoding – which causes longer strings with no repeating characters – that allows the unmanipulated 340 to score a bit higher than it should. Or even the bigrams/repeating fragments causing this. Or if there really is something there sitting horizontally, garbled up by some process.
Next is a not so strongly hill climbed alteration of the 340 where its rows have been shifted around and it scores 20688. Notice that the 340’s plaintext is still mainly intact (the plaintext you get when you try to solve the 340 normally). Though Ioc is high and Entropy is fairly low, bigrams up to 31.
AZdecrypt 0.993 (Practical Cryptography 5-grams) Score: 20687.76 Ioc: 0.07714732 Entropy: 3.854225 Chi-square: 51.57744 Characters: 340 Letters: 19 fadgeearisedmniat emandsteforearsth santelemforttheop edcantocarrorseli ttorperatinlnpros sotainstoabanderf anolesonecityfast othpollfolesannai seconteitispereds debuiceaplanocost careemoteadaneltt hantrumpetrcrefor fromrepleslieispa ratimesitseletora teachifionendther estersinorldeiamo nsspectingsitthat sthercisimporator mentatchtreadymea llhascentofurnatm Multiplicity: 0.1852941 Characters: 340 Symbols: 63 Bigrams: 31 Sequential: 4246 |c.3zBK(Op^.fMqG2 z69Sy#+N|5FBc(;8R _9M+ztjd|5FP+&4k/ By:cM+UZGW()L#zHJ ++)WCzWcPOSHT/()p #5+Kq%;2UcXGV.zL| >MDHNpkSzZO8A|K;+ U+R/5tE|DYBpbTMKO -zlUV+^J+Op7<FBy- yBX1*:49CE>VUZ5-+ lGFN^f524b.cV4t++ RcT+L16C<+FlWB|)L |FkdW<7tB_YOB*-Cc (G2Jfj#O+_NYz+@L9 2<clRJ|*5T4M.+&BF Np+B(#O%DWY.<*Kf) Spp7^l8*V3pO++RK2 p8R^FlO-*dCkF>2D( d<M+b+ZR2FBcyA64K HER>pl^VPk|1LTG2d
A bit more on this, I really don’t know what to think. Score is 21065 and the main elements of the aforementioned 340 "plaintext" still show up, hill climbed a bit more thoroughly allowing more stuff. Legend: operation(dimension_x,dimension_y,do(1)/undo(2),period). The sequential measurement is non-repeats, not the m_2s_cycles.
Perhaps this kind of "horizontal" moldability is normal?
AZdecrypt 0.993 (Practical Cryptography 5-grams) 1: Manipulation operation(s): PeriodRows(170,2,1,2), PeriodRows(34,10,2,7) 2: Manipulation operation(s): PeriodRows(2,170,1,169) 3: Manipulation operation(s): OffsetRows(2,170,162), PeriodRows(10,34,2,32) 4: Manipulation operation(s): OffsetRows(10,34,23), PeriodRows(85,4,2,3) 5: Manipulation operation(s): PeriodRows(20,17,2,15) Score: 21064.99 Ioc: 0.07313899 Entropy: 3.885914 Chi-square: 47.4443 Characters: 340 Letters: 18 mieispainagosonec itseealisedcnnate llantofastlotands toabandercarlorle ginsspectingflati calitsomethrement itchtrealsmdaseco nteitisitthathant rumpetrcreforttor peratingnelossent eramfortthdoesthe rcisimporitalfrom repressperelsothe orafamesinnaiteac hifiondsthcaroeco ndtherementdidand rgalltoforealtthi scentofurnatmoste llidarmdeiacolebu ildepainocostfadg Multiplicity: 0.1852941 Characters: 340 Symbols: 63 Bigrams: 24 Sequential: 3990 YOB*-Cc>MDHNpkSzZ O8AzBK(Op^.fMqG2B y:cM+U|K;+#5+Kq%; 2UcXGV.zLZGW()L#z HJSpp7^l8*V3|(G2J fj#O+_NYz+@L9d<M+ b+ZR2FBcyA64K-zlU V+^J+OpO++RK2RcT+ L16C<+FlWB|)L++)W CzWcPOSHT/()p_9M+ ztjd|5FP+&4k/p8R^ FlO-*dCkF>2D(|Fkd W<7tB_p7<FBy-U+R/ 5tE|DYBpbTMKO2<cl RJ|*5T4;8RlGFN^f5 M.+&BFz69S24b.cV4 tHEy#+N|5FBc(++R> pl^VPk|1LTG2dNp+B (#O%DWY.<*Kf)yBX1 *:49CE>VUZ5-+|c.3
It’s something that still bothers me. I wonder if it is the encoding – which causes longer strings with no repeating characters – that allows the unmanipulated 340 to score a bit higher than it should. Or even the bigrams/repeating fragments causing this.
Maybe I should repeat the random shuffle experiment, but keep only the shuffles that have the same number of repeated bigrams/fragments, and that have similar stretches of no repeating characters. Then we can see if that reduces the statistical significance of Z340’s score.
mie is pain ago so necits eealised cnn a tell anto fast lot andsto a band er carl or leg insspecting flat i cal it some thre ment it chtreals mdaseconteit is it that han trumpet rcrefortt orperating nelos sent eram fortth does therc is imporital from repress perel so theor a fame sinna i teac hifi on dsth car oecond there ment did and r gall to foreal t
thi scent of urnat most ellid arm deiacole build e pain o cost fad g
Lots of different permutations can be made .. Just looking to see if anything pops out.. Not much
Trumpet / band
Pain twice
Insspecting flat..
I Teac hi fi on dsth car.
Also read as I teach if I
A bit more on this, I really don’t know what to think. Score is 21065 and the main elements of the aforementioned 340 "plaintext" still show up, hill climbed a bit more thoroughly allowing more stuff.
I looked in this some more and think to know what is going on. Because of the freedom of the operations, elements of the 340’s plaintext that score highly are much less likely to be washed away because of the hill climbing process. Some of the words/elements Mr lowe mentioned score highly and therefore are kept creating some sense of illusion. I had a "solution" scoring over 22k yesterday and it kept going up easily, it was basicly n-gram spagetthi with some of the stronger elements of the 340’s "plaintext" still intact. It builds around that.
It’s something that still bothers me. I wonder if it is the encoding – which causes longer strings with no repeating characters – that allows the unmanipulated 340 to score a bit higher than it should. Or even the bigrams/repeating fragments causing this.
Maybe I should repeat the random shuffle experiment, but keep only the shuffles that have the same number of repeated bigrams/fragments, and that have similar stretches of no repeating characters. Then we can see if that reduces the statistical significance of Z340’s score.
That sounds perfect!
"n-gram spaghetti" is my new favorite phrase! ![]()
I think it is related to "word salad"
Maybe word-level ngrams would help here, since you can use them to exclude improbable combinations of words.
"n-gram spaghetti" is my new favorite phrase!

I think it is related to "word salad"
Maybe word-level ngrams would help here, since you can use them to exclude improbable combinations of words.
Hehehe ![]()