This last week I have been working on a spreadsheet suite that creates bifid messages with different possible variables.

EDIT:

[b]Question: How easy / difficult is it to make a bifid message with a symbol count distribution and period 15/19 repeat stats comparable to the 340?

Short Answer: Not particularly easy, but probably not impossible. Bifid transposes the ciphertext at a period of one half the plaintext period. Because transposition is contained within message "chunks" ( the plaintext period ), similar to a two row railfence cipher or series of two column inscription rectangles, the opportunities for creating period 15/19 repeats are substantially diminished. Transposition doesn’t occur across more than one plaintext period.

With a plaintext period of 30, inscription of ciphertext 1 right left top bottom, and cyclic encoding of all homophonic ciphertext 2, the number of period 19 repeats will only be about half of 340 period 19 repeats. That makes sense, because of the short period.

EDIT: By ciphertext 1, I mean the set of symbols created by the bifid process, which look like regular letters. by ciphertext 2, I mean the 63 symbols that look like numbers.

However, increasing the plaintext period to 38, inscription of ciphertext 1 left right top bottom, and cyclic encoding of all homophonic ciphertext 2, the number of period 19 repeats should increase. And mapping one to three ciphertext 2 to a few different ciphertext 1, to more closely mimic 340 symbol count distribution and cycle stats, can increase the period 19 repeat counts to almost 340 stats.

Here is the cipher:

1. Choose a random message from Jarlve’s 100 plaintext library.

2. Choose a period and use a polybius square to transpose and encode the plaintext into ciphertext 1.

3. For plaintext period 30 ( which creates ciphertext 1 period 15 repeats ), inscribe the message into a 17 x 20 rectangle right left top bottom. For a plaintext period of 38 ( which creates ciphertext period 19 repeats ), inscribe left right top bottom.

4. Cyclically encode with about 63 homophonic ciphertext 2 symbols. To approximate 340 cycle stats, randomly select ciphertext 2 symbols within a homophonic symbol group 10 % of the time in rows 1-5, 20% of the time in rows 6-10, 30% of the time in rows 11-15, and 40% of the time in rows 16-20. EDIT: The keys are "flat" and inefficient, and look similar to below, which diffuse the high frequency ciphertext 1 as little as possible ( ciphertext 1 high frequency symbols are high frequency because they appear more often in the plaintext period 1 repeats) .

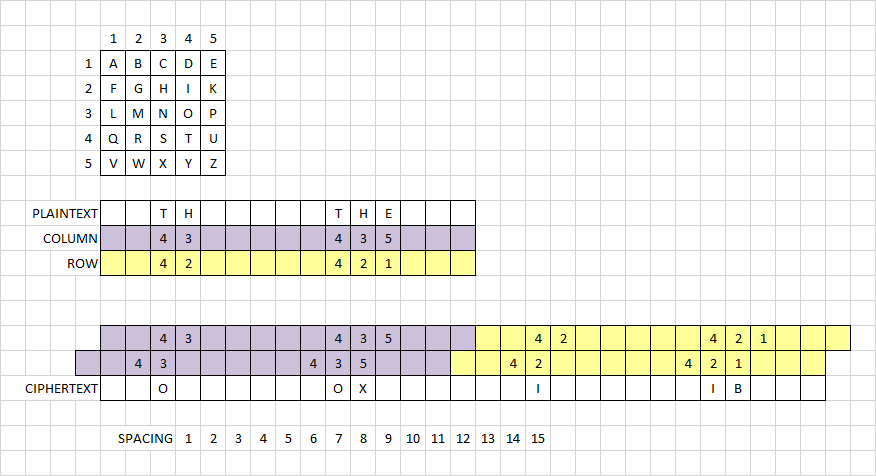
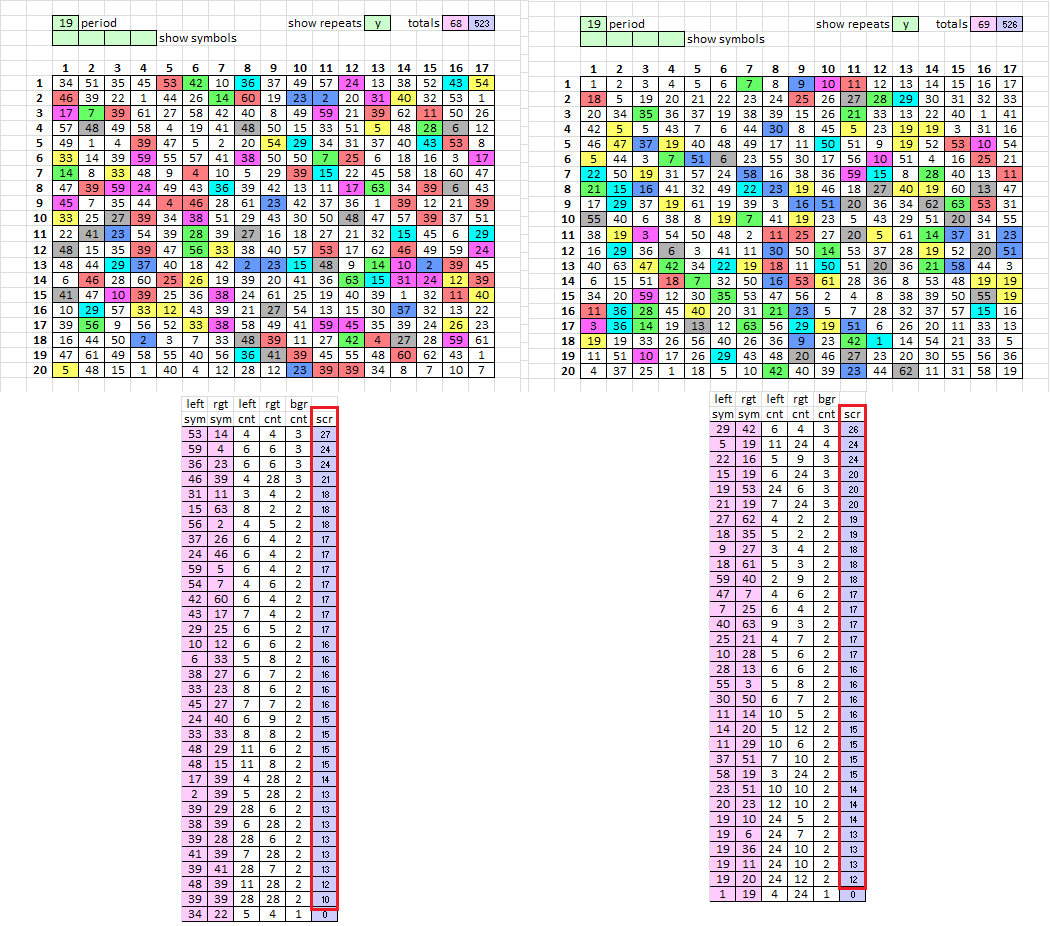
For simple example of bifid, the polybius square is at the top. The plaintext period is set to 12. And I encode the message "I like killing" with the first twelve plaintext highlighted yellow to show what happens. The ciphertext are are highlighted yellow at the bottom.

Plaintext………..Ciphertext
IL………………..D6M ( M is 6 spaces to the right of D )
IK………………..Y6G
EK………………..Z6F
IL………………..D6M
LI………………..Q6H
NG……………….H6H

See how IL is repeated, but changes to DM repeated, where the D is 6 spaces before the M? That’s how it works, except that to create period 15 or period 19 repeats, I have to make the plaintext period 30 or 38.

Also, bifid is very similar to a two row railfence, except that it uses the polybius square to make all of the ciphertext 1 polyalphabetic. As a matter of fact, instead of using the transposition of coordinates as described on websites, you can encode two symbols at a time, and then use a two row railfence cipher to get the exact same result! Provided that the plaintext period is an even number instead of an odd number.

Bifid with an even plaintext period also smooths out the distribution of ciphertext 1 count as compared to plaintext count. But it doesn’t flatten it out. Instead, it makes a smoother but sloping distribution.

I made a lot of messages and some of the ciphertext 1 distributions are even smoother than this one. Here is one for the "Ferengi Rules" message:

I have to do some things now, but will return soon. The hard part is done, and all I have to do is make variable selections on my spreadsheet and click on "calculate now" a lot of times to gather statistics. As an aside, I should look at odd numbered periods to see what happens to the ciphertext 1 distribution.

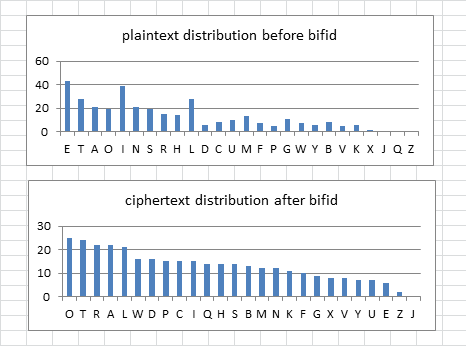
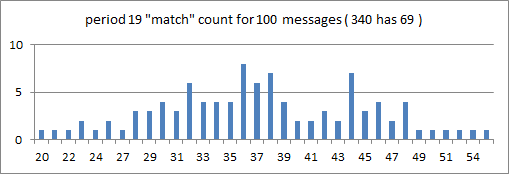
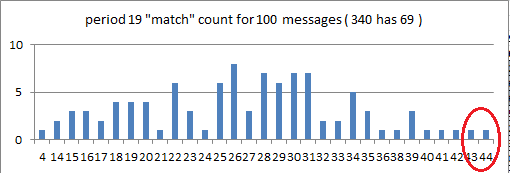
I made 100 messages with a plaintext period of 30, and inscribed right left top bottom to make the period 15 repeats / matches look like period 19 repeats / matches. All ciphertext 2 encoding homophonic. Here is a distribution. The mean is 33 and standard deviation is 7.1. The highest was 51, but that is not close to the 340, which has 69 period 19 matches. That would be 5 sigmas.

So the Zodiac 340 is not a plaintext period 30 mirrored bifid with all homophonic ciphertext 2 encoding.

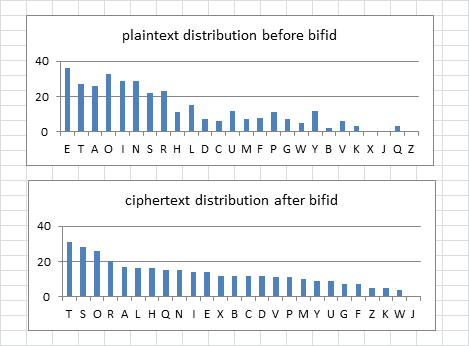
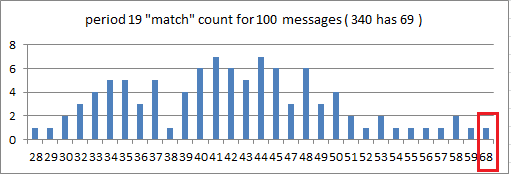
EDIT: I made 100 messages with a plaintext period of 38, and inscribed left right top bottom so that there are a lot of period 19 repeats / matches. All ciphertext 2 encoding homophonic. Here is a distribution. As expected because of the higher plaintext period, the mean increased and is 37. The standard deviation is 7.6. There were several messages with period 19 match counts in the low 50’s, but that is still not close to the 340, which has 69 period 19 matches. That would be 4.2 sigmas.

So the Zodiac 340 is not a plaintext period 38 with all homophonic ciphertext 2 encoding.

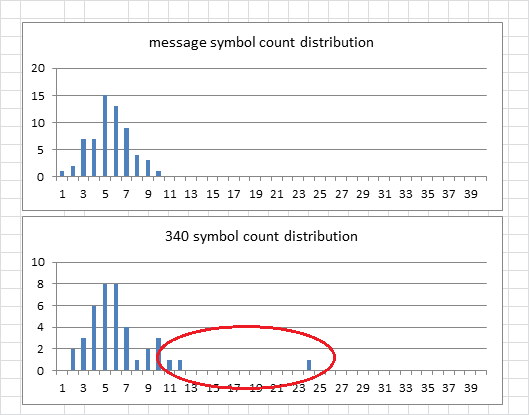
Alright, so here is a typical ciphertext 2 count distribution, and the last one that I made. They all look very similar to each other, and very similar to the 340 symbol count distribution. Except that there aren’t any high count symbols like the +, and typically there aren’t many with symbol counts higher than 10. That’s what I am going to do next, to see if I can get closer to 340 stats.

I made two ciphertext 2 symbols polyalphabetic. I mapped the first symbol to the four highest frequency ciphertext 1, and mapped the second symbol to the fifth and sixth highest frequency ciphertext 1. Then I made 100 messages.

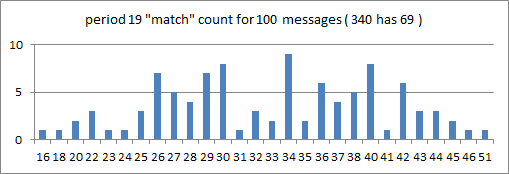
The mean number of period 19 matches went up to 43, and the standard deviation was 7.5.

One of the 100 messages had stats comparable to the 340, with 68 period 19 matches. That will be smokie31.

Here is the key to smokie31:

A 1 2 3 48
B 4 5 6
C 7 8 9
D 10 11 12
E 13 14
F 15 16
G 17 18
H 19 20
I 21 22 23 39
J
K 24 25
L 26 27
M 28 29 30
N 31 32 33
O 34 35 36 39
P 37 38
Q 39 40 41
R 42 43 44
S 45 46 47 39
T 48 49 50
U 51 52
V 53 54
W 55 56
X 57 58 59
Y 60 61
Z 62 63

Note that symbols 39 and 48 map to more than one ciphertext 1. That would be "double polyalphabetism", but just for those two symbols. Here is the message:

34 51 35 45 53 42 10 36 37 49 57 24 13 38 52 43 54
46 39 22 1 44 26 14 60 19 23 2 20 31 40 32 53 1
17 7 39 61 27 58 42 40 8 49 59 21 39 62 11 50 26
57 48 49 58 4 19 41 48 50 15 33 51 5 48 28 6 12
49 1 4 39 47 5 2 20 54 29 34 31 37 40 43 53 8
33 14 39 59 55 57 41 38 50 50 7 25 6 18 16 3 17
14 8 33 48 9 4 10 5 29 39 15 22 45 58 18 60 47
47 39 59 24 49 43 36 39 42 13 11 17 63 34 39 6 43
45 7 35 44 4 46 28 61 23 42 37 36 1 39 12 21 39
33 25 27 39 34 38 51 29 43 30 50 48 47 57 39 37 51
22 41 23 54 39 28 39 27 16 18 27 21 32 15 45 6 29
48 15 35 39 47 56 33 38 40 57 53 17 62 46 49 59 24
48 44 29 37 40 18 42 2 23 15 48 9 14 10 2 39 45
6 46 28 60 25 26 19 39 20 41 36 63 15 31 24 12 39
41 47 10 39 25 36 38 24 61 25 19 40 39 1 32 11 40
10 29 57 33 12 43 39 21 27 54 13 15 30 37 32 13 22
39 56 9 56 52 33 38 58 49 41 59 45 35 39 24 26 23
16 44 50 2 3 7 33 48 39 11 27 42 4 27 28 59 61
47 61 49 58 55 40 56 36 41 39 45 55 48 60 62 43 1
5 48 15 1 40 4 12 28 12 23 39 39 34 8 7 10 7

I don’t know what the plaintext is because I forgot to save it. But it is one of the Jarlve 100 library. However, we have the key, the period, and the polybius square. So is can be solved with those. We could just solve the first 38 positions and figure out what message it is.

So, it is possible to use bifid to create comparable period 19 340 stats, given that the plaintext period is 38, transcription is left right top bottom, and there are two ciphertext 2 polyalphabetic symbols.

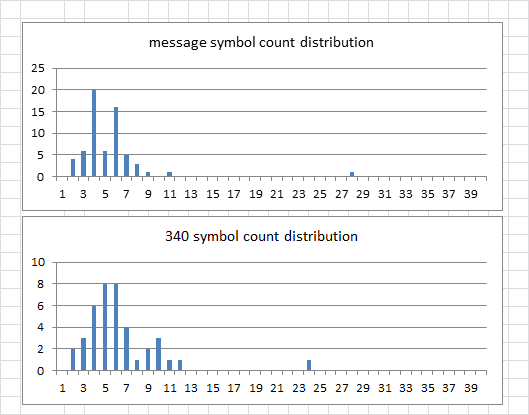
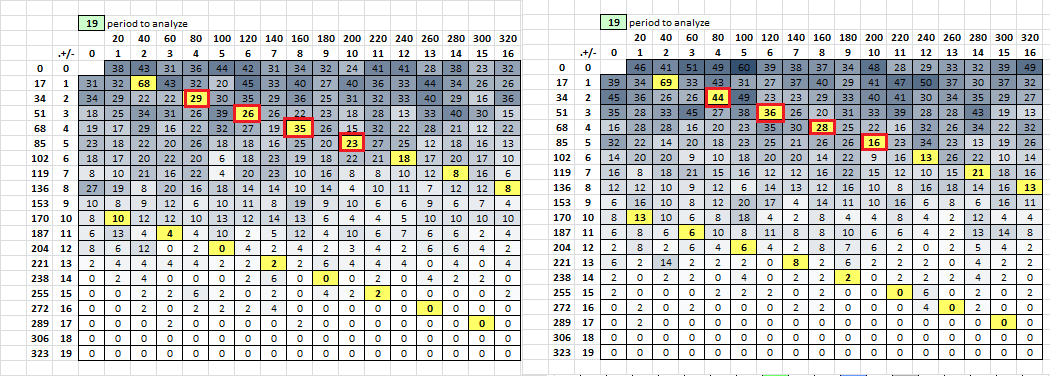
What I have to do now is take a closer look at smokie31 to compare period 38, 54, etc. stats. Smokie31 is not quite as cyclic as the 340, with a score of 50228.

Here is the smokie31 symbol count distribution:

Here are the period 19 repeats ( or matches ). Smokie31 is on the left, and the 340 is on the right. Note that the scores for the repeats / matches are almost identical.

Here is the all period analysis. Smokie31 on the left, Z340 on the right.

For smokie31, there are only 29 period 38 matches. For the 340, there are 44. For smokie31, there are only 26 period 57 matches. For the 340, there are 36. That is probably because chunks of 38 plaintext were transposed with the bifid, not allowing for period 38 or period 57 matches. However, for periods 75 and 95, smokie31 has more matches than the 340.

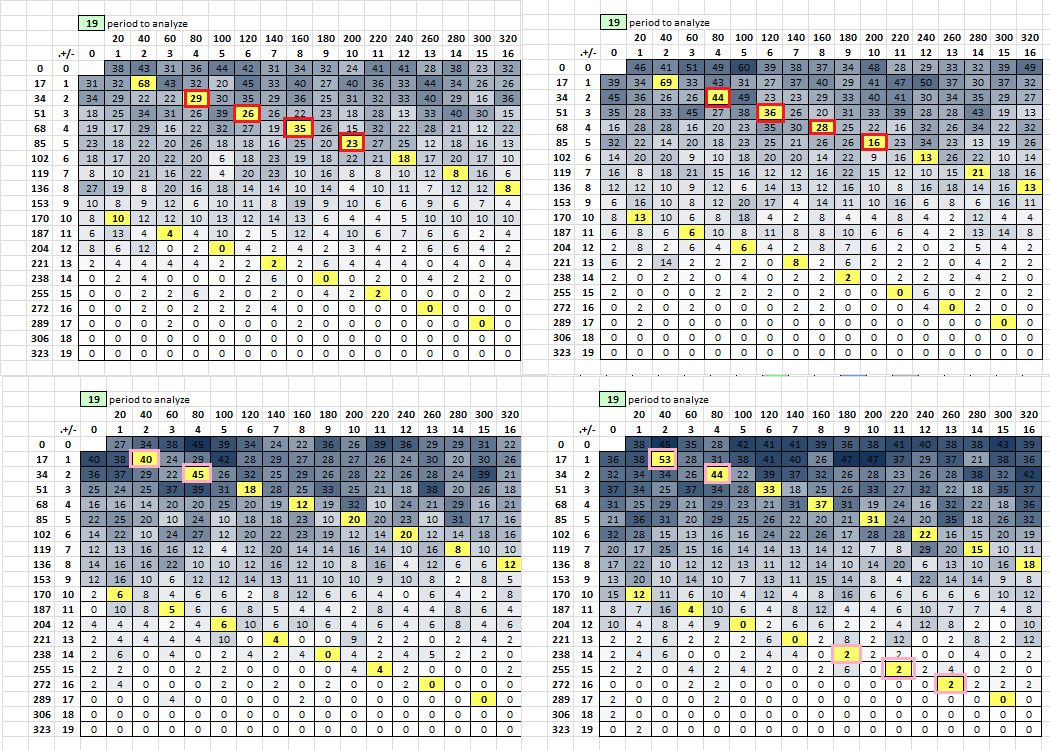
EDIT: Now I am going to make bifid messages, exactly like smokie31, and try to match period 38 stats.

I made 100 messages with the same settings as smokie31, to find out if I could make a message with a comparable count of period 38 matches. And I could. There were a few with counts in the lower 40’s.

I saved the top two, smokie31a and smokie31b, at the bottom left and right. Smokie31a has 45 period 38 matches, but only 40 period 19 matches. Smokie31b has 44 period 38 matches, but 53 period 19 matches. They both have a couple of repeat stats that reach down into the lower levels of the spreadsheet. So, it would seem that although the plaintext period chunks are transposed independently of each other, perhaps the alignment of the period 19 repeats occasionally line up with each other. But neither message had high scores for both period 19 and period 38 messages.

I am getting tired and probably won’t take this much farther.

Yes, it is possible to make a bifid message that has a similar symbol count distribution and period 19 stats as the 340. But you might have to make a couple of ciphertext 2 symbols map to high frequency ciphertext 1 symbols, to increase the counts of period 19 matches. And even then, it may be very difficult to make such a message that also has a comparable count of period 38 repeats or matches. Any cipher that transposes plaintext in small chunks instead of in large chunks or all at once, greatly lowers the probability of making a message that has 340 stats. But it is not impossible.

I like the bifid, sort of, and see untransposing message chunks and then making small changes to a polybius square over and over again until finally getting a solution. But it seems that combining bifid with another cipher type, such as homophonic substitution, would make solving very difficult.

I keep a log of things I’ve observed about Z340, but it’s very long and full of very minor "oddities" that are very likely just things that happened by pure chance. For example, I noticed that you get a stable solve (i.e. the auto-solver frequently converges on the exact same solution) if you use bifid with the key "ZODIAC", but that stable solve is gibberish and its overall score is far from a normal English text. I should go over my log again and try to cull the most significant "finds".

Daikon said it here: viewtopic.php?f=81&t=2617&p=38982&hilit=bifid#p38982

I wonder how to solve a bifid with homophonic substitution combined? How could anybody figure out how to do that?

Thanks allot for all the work on this smokie!

However, increasing the plaintext period to 38, inscription of ciphertext 1 left right top bottom, and cyclic encoding of all homophonic ciphertext 2, the number of period 19 repeats should increase. And mapping one to three ciphertext 2 to a few different ciphertext 1, to more closely mimic 340 symbol count distribution and cycle stats, can increase the period 19 repeat counts to almost 340 stats.

So bifid on its own does not produce the period we are looking for, but if you add in transposition it can be done.

Jumping ahead to smokie31 (which I think is very interesting to compare versus the 340). It appears to be similar in stats to the 340 but important differences can be noted.

When looking at the smokie31 just as it is with a test that can spot vigenere/bifid nothing jumps out. But when adding in the transposition element (because we know that) it can be spotted. Surely it was there after undoing period 19. This is something that I’ve looked for in the 340 with various of the more potent un-transpositions and haven’t found anything yet that could point in this direction.

Another difference is that after mirroring of flipping the smokie31 period 19 shifts to 46. While with the 340 period 19 shifts to period 15, which seems to be more consistent with regular transposition.

So the Zodiac 340 is not a plaintext period 30 mirrored bifid with all homophonic ciphertext 2 encoding.
So the Zodiac 340 is not a plaintext period 38 with all homophonic ciphertext 2 encoding.

I feel the same.

I am getting tired and probably won’t take this much further.

Thanks again for all your work on this!

I wonder how to solve a bifid with homophonic substitution combined? How could anybody figure out how to do that?

I haven’t looked into it but if you can outline me a method for just substitution I could possibly add an operation to AZdecrypt’s manipulation solver so that you can try out different keywords manually. That’s as far as I’m willing to take it given the meager evidence of bifid being used in the 340.

Thanks allot for all the work on this smokie!

I am getting tired and probably won’t take this much further.

Thanks again for all your work on this!

I want to second this. Thanks, smokie, for your thorough and extensive work!

No problem. I think that the take away is that there are other ciphers that cause transposition. Any cipher that moves stuff around may do that, and create a ciphertext period. But, when stuff is moved around in small chunks, the exposure that each plaintext has to becoming a member of a period x bigram repeat is diminished.

The 340 would therefore likely transpose large chunks of plaintext to get the high stats. I will continue to look for a cipher that creates two distinct periods to explain the period 29 issue. It may just be created by the mirroring process, and I was able to duplicate that phenomenon with other periods.

So bifid on its own does not produce the period we are looking for, but if you add in transposition it can be done. . . . I haven’t looked into it but if you can outline me a method for just substitution I could possibly add an operation to AZdecrypt’s manipulation solver so that you can try out different keywords manually. That’s as far as I’m willing to take it given the meager evidence of bifid being used in the 340.

Bifid is a transposition cipher and also a digraph cipher, similar to playfair. It diffuses the plaintext and makes all symbols polyalphabetic. And it transposes them at a period that is half of the size of the plaintext chunk that the encoder chooses. Bifids that I see in examples have a plaintext period of 5, 6, 10, 11 and 12. I haven’t seen anything like period 38, which Daikon mentioned would be unusual.

For now I wouldn’t bother messing around with bifid. It is not particularly easy to make a message with stats similar to the 340, but it can be done.If the 340 is a bifid, then it is likely a statistical anomaly.

I am excited about your hill climbing of polyalphabetic symbols. If you want a message that has a few polyalphabetic symbols for a test, but without transposition, let me know. Otherwise, I am planning on helping to fine tune a partial solution of an imperfectly untransposed message that we get with your new hill climber, when and if the time comes.That is what I am hoping for. Then to move on to something else, possibly not cryptography related. In the meantime, I will continue to work on some of the ideas that we have worked on this last year.

If you want a message that has a few polyalphabetic symbols for a test, but without transposition, let me know.

Yes, could really use a few new wildcard ciphers with original plaintexts and without transposition. One cipher with 6 wildcards that cover about 60 symbols. And another with 8 wildcards that cover about 80 symbols. Tyvm!

O.k., I will get started and find some new plaintext. There will be six poly symbols with a total count of about 60, and about 57 symbols with a total count of about 280.

Here is smokie32A, which has some randomization of symbol selection within cycle groups:

22 12 57 1 47 5 2 7 29 25 36 50 23 13 34 26 37
27 47 50 44 60 40 17 31 41 55 14 58 28 52 24 15 56
16 45 61 22 22 12 38 19 18 42 46 20 25 55 12 39 23
26 49 40 41 53 32 59 24 27 50 13 3 48 48 12 41 58
22 14 57 4 49 28 36 50 23 15 43 53 6 33 12 8 9
42 7 30 8 42 37 18 16 40 48 25 38 21 12 55 13 44
60 52 24 26 39 21 27 35 43 31 28 7 12 22 12 38 20
14 55 15 45 61 5 41 11 60 22 16 58 1 48 59 1 32
29 25 36 21 11 42 31 39 50 23 12 57 24 26 51 13 52
26 33 14 44 8 42 45 44 28 10 41 45 58 12 22 22 50
23 15 18 16 12 31 25 38 19 42 17 59 3 32 30 27 39
19 27 12 49 53 36 33 28 20 22 50 4 37 10 12 38 1
46 35 13 11 19 54 2 44 44 3 50 22 12 40 6 12 7
29 52 23 14 31 40 36 20 24 41 43 15 9 18 42 45 5
53 32 33 16 51 31 4 47 12 12 51 13 46 25 36 21 22
26 48 6 45 1 27 37 23 14 19 2 62 14 10 54 43 3
52 51 24 14 12 37 40 45 34 42 53 49 17 2 8 14 18
42 45 50 61 60 14 1 44 40 28 51 23 1 9 52 4 30
15 36 23 12 34 22 40 33 16 3 44 12 31 22 4 50 29
25 36 9 41 17 40 35 26 32 12 58 12 49 22 27 9 11

And here is smokie32B, with all perfect cycles.

22 12 57 1 47 5 2 7 29 25 36 50 23 13 34 26 37
27 48 51 44 60 40 17 31 41 55 14 58 28 52 24 15 56
16 45 61 22 22 12 38 21 18 42 46 20 12 55 12 39 23
26 49 40 40 53 32 59 24 27 50 13 3 47 48 12 41 31
22 14 57 4 49 28 36 51 23 15 43 54 6 33 12 8 9
42 7 30 8 40 37 17 16 40 47 25 38 21 12 56 13 44
60 52 24 26 39 19 27 35 43 31 28 7 12 22 12 12 20
14 55 15 45 61 5 41 10 60 22 16 58 2 48 59 2 32
29 25 36 21 11 42 31 37 50 23 12 57 24 26 51 13 52
27 33 14 44 8 40 46 44 28 9 41 45 58 12 22 22 50
23 15 18 15 12 31 25 38 19 42 17 59 3 32 29 26 39
20 27 12 49 53 36 33 28 21 24 51 4 37 10 12 38 1
46 34 13 11 19 54 2 44 44 3 52 22 12 40 6 4 7
29 22 23 14 31 40 39 20 24 41 43 15 9 18 42 45 5
53 32 33 16 50 31 12 47 12 12 51 13 46 25 36 21 22
26 48 6 44 1 27 37 23 14 19 2 62 15 10 54 43 3
52 22 24 16 12 38 40 45 35 41 53 49 17 4 8 13 18
42 46 50 61 60 14 12 44 40 28 51 22 1 11 52 2 30
15 39 23 12 34 22 40 31 16 3 45 12 57 24 4 50 29
25 36 44 41 17 47 35 26 32 12 58 12 48 22 27 9 9

They both have the same plaintext, key, and 5 polyalphabetic symbols covering 60-70 count across the entire message.

I got the solution by expanding all possible selections of 2 symbols (62 choose 2 = 1891 different cipher texts), running them all through azdecrypt, and by googling for recognizable phrases in the results.

I won’t post the solution, to avoid spoiling it for Jarlve

It occurs to me that to secure the plaintext a bit further, you should create your own message so I can’t google for recognizable passages. Jarlve’s method of progressive expansion should still be able to recover the message, I believe.

So, unmodified Z340’s azdecrypt score of 20,237 is 2.7 sigma away from the mean in experiment A (full shuffles), but only 1.4 sigma away from the mean in experiment B (per-row shuffles). It suggests that the scores may indeed be tied to ngrams and areas of non-repeating symbols.

Caveat: Experiment A had 10,000 shuffles and Experiment B only had 1,000. Also, I ran experiment A in AZdecrypt 0.99, and experiment B in AZdecrypt 0.992c. So there may be some differences caused by those experimental changes. I’ll soon re-run experiment A under the same conditions as experiment B just to be sure.

Thanks for doing that doranchak. Smart to keep the row order! I once hill climbed row swaps in the 340 to maximize non-repeats and when I ran these through ZKDecrypto they scored quite a bit higher.