I got the solution by expanding all possible selections of 2 symbols (62 choose 2 = 1891 different cipher texts), running them all through azdecrypt, and by googling for recognizable phrases in the results.
I won’t post the solution, to avoid spoiling it for Jarlve
It occurs to me that to secure the plaintext a bit further, you should create your own message so I can’t google for recognizable passages. Jarlve’s method of progressive expansion should still be able to recover the message, I believe.
Nice one doranchak. Did you get both solutions?
Thanks smokie. I’ll fire up both ciphers and the 340 today.
Smokie, I tested your ciphers without expanding any symbols and smokie32a scores 22627 and the smokie32b scores 22103. Both are quite readable without expanding any wildcard symbols, I don’t think it will be very useful to run these through.
smokie32a: AZdecrypt 0.993 (Practical Cryptography 5-grams) Score: 22626.78 Ioc: 0.0656776 Entropy: 4.136947 Chi-square: 22.63911 Characters: 340 Letters: 22 sewasbackinthemin istryafloverithev eryssengfordivenh isaoulwhiteatteor sewasinthepublecd ockconfeatingever ythingimplicesend everybodyseratwal kingdolnthewhitet ilercorridorresst hefeelingofwalkin giesunlidstandena rmedguarratseabec kthelandhopedforb ulletlaseeterings itbrainhegamedupa ttheenarmousfacef ortyyearaithadtak enhemsalearelsatk indofamileressidd Multiplicity: 0.1823529 Characters: 340 Symbols: 62 Bigrams: 41 Sequential: 3918 22 12 57 1 47 5 2 7 29 25 36 50 23 13 34 26 37 27 47 50 44 60 40 17 31 41 55 14 58 28 52 24 15 56 16 45 61 22 22 12 38 19 18 42 46 20 25 55 12 39 23 26 49 40 41 53 32 59 24 27 50 13 3 48 48 12 41 58 22 14 57 4 49 28 36 50 23 15 43 53 6 33 12 8 9 42 7 30 8 42 37 18 16 40 48 25 38 21 12 55 13 44 60 52 24 26 39 21 27 35 43 31 28 7 12 22 12 38 20 14 55 15 45 61 5 41 11 60 22 16 58 1 48 59 1 32 29 25 36 21 11 42 31 39 50 23 12 57 24 26 51 13 52 26 33 14 44 8 42 45 44 28 10 41 45 58 12 22 22 50 23 15 18 16 12 31 25 38 19 42 17 59 3 32 30 27 39 19 27 12 49 53 36 33 28 20 22 50 4 37 10 12 38 1 46 35 13 11 19 54 2 44 44 3 50 22 12 40 6 12 7 29 52 23 14 31 40 36 20 24 41 43 15 9 18 42 45 5 53 32 33 16 51 31 4 47 12 12 51 13 46 25 36 21 22 26 48 6 45 1 27 37 23 14 19 2 62 14 10 54 43 3 52 51 24 14 12 37 40 45 34 42 53 49 17 2 8 14 18 42 45 50 61 60 14 1 44 40 28 51 23 1 9 52 4 30 15 36 23 12 34 22 40 33 16 3 44 12 31 22 4 50 29 25 36 9 41 17 40 35 26 32 12 58 12 49 22 27 9 11
UPDATE: Experiment conditions match now, so I removed the original post and replaced it with this one.
Maybe I should repeat the random shuffle experiment, but keep only the shuffles that have the same number of repeated bigrams/fragments, and that have similar stretches of no repeating characters. Then we can see if that reduces the statistical significance of Z340’s score.
OK – I finally got around to doing this. Approach:
1) Shuffle each row of the Z340 one at a time. This preserves the per-row number of repeated symbols.
2) Keep only the shuffles that have exactly 25 bigram repeats (and 46 total repeating bigrams), to match the original Z340.
3) Run 1,000 of those shuffles in azdecrypt 0.992c using 30 restarts and 1,000,000 iterations.
Here are the resulting statistics:
Experiment B (Per-row shuffles of Z340):
- Min score: 19678
- Max score: 20641
- Mean score: 20116
- Score Std Dev: 150
- Min ioc: 657
- Max ioc: 830
- Mean ioc: 746
- ioc Std Dev: 29
- Min score: 19298
- Max score: 20570
- Mean score: 19868
- Score Std Dev: 168
- Min ioc: 665
- Max ioc: 900
- Mean ioc: 746
- ioc Std Dev: 30
[/list:u:l0zc8s50]
For comparison, here are the results for 1,000 full shuffles of Z340:
Experiment A (Full shuffles of Z340):
[/list:u:l0zc8s50]
So, unmodified Z340’s azdecrypt score of 20,327 is 2.7 sigma away from the mean in experiment A (full shuffles), but only 1.4 sigma away from the mean in experiment B (per-row shuffles). It suggests that the scores may indeed be tied to ngrams and areas of non-repeating symbols.
Here’s are ZIP files of the ciphers and results:
Experiment A: https://drive.google.com/open?id=0Bx2Zx … HRWN3B2YTA
Experiment B: https://drive.google.com/open?id=0Bx2Zx … UFrZk03bjA
Smokie, I tested your ciphers without expanding any symbols and smokie32a scores 22627 and the smokie32b scores 22103. Both are quite readable without expanding any wildcard symbols, I don’t think it will be very useful to run these through.
smokie32a: AZdecrypt 0.993 (Practical Cryptography 5-grams) Score: 22626.78 Ioc: 0.0656776 Entropy: 4.136947 Chi-square: 22.63911 Characters: 340 Letters: 22 sewasbackinthemin istryafloverithev eryssengfordivenh isaoulwhiteatteor sewasinthepublecd ockconfeatingever ythingimplicesend everybodyseratwal kingdolnthewhitet ilercorridorresst hefeelingofwalkin giesunlidstandena rmedguarratseabec kthelandhopedforb ulletlaseeterings itbrainhegamedupa ttheenarmousfacef ortyyearaithadtak enhemsalearelsatk indofamileressidd Multiplicity: 0.1823529 Characters: 340 Symbols: 62 Bigrams: 41 Sequential: 3918 22 12 57 1 47 5 2 7 29 25 36 50 23 13 34 26 37 27 47 50 44 60 40 17 31 41 55 14 58 28 52 24 15 56 16 45 61 22 22 12 38 19 18 42 46 20 25 55 12 39 23 26 49 40 41 53 32 59 24 27 50 13 3 48 48 12 41 58 22 14 57 4 49 28 36 50 23 15 43 53 6 33 12 8 9 42 7 30 8 42 37 18 16 40 48 25 38 21 12 55 13 44 60 52 24 26 39 21 27 35 43 31 28 7 12 22 12 38 20 14 55 15 45 61 5 41 11 60 22 16 58 1 48 59 1 32 29 25 36 21 11 42 31 39 50 23 12 57 24 26 51 13 52 26 33 14 44 8 42 45 44 28 10 41 45 58 12 22 22 50 23 15 18 16 12 31 25 38 19 42 17 59 3 32 30 27 39 19 27 12 49 53 36 33 28 20 22 50 4 37 10 12 38 1 46 35 13 11 19 54 2 44 44 3 50 22 12 40 6 12 7 29 52 23 14 31 40 36 20 24 41 43 15 9 18 42 45 5 53 32 33 16 51 31 4 47 12 12 51 13 46 25 36 21 22 26 48 6 45 1 27 37 23 14 19 2 62 14 10 54 43 3 52 51 24 14 12 37 40 45 34 42 53 49 17 2 8 14 18 42 45 50 61 60 14 1 44 40 28 51 23 1 9 52 4 30 15 36 23 12 34 22 40 33 16 3 44 12 31 22 4 50 29 25 36 9 41 17 40 35 26 32 12 58 12 49 22 27 9 11
Oops, sorry about that. I was in a hurry during my lunch break and didn’t have time to test it. I will make a harder one. I think that smokie32A had 60 poly symbols and smokie32B had 69. Your results surprised me.
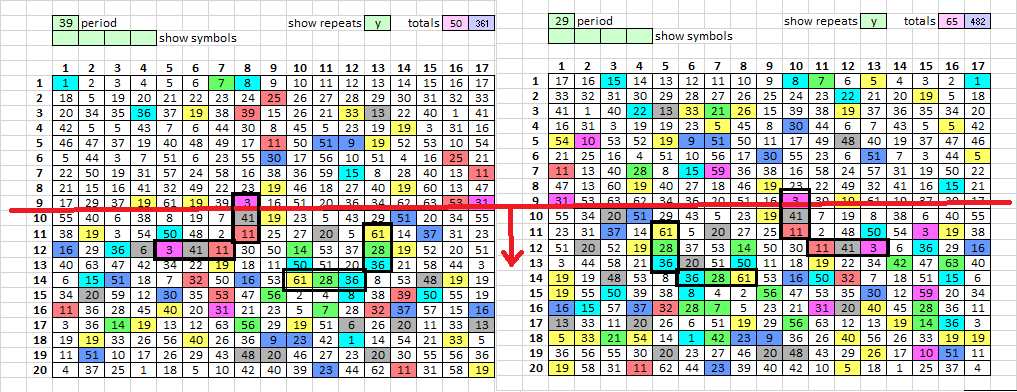
I hate to say it, but sometimes I dream about the 340. I let my subconscious mind work on trying to figure out what type of ciphers Zodiac used. Last night my subconscious worked a little bit on the period 29/39 issue.
On the left is period 39, on the right, period 29 (mirrored). They are predominately in the bottom half of the message. So we know that period 15/19 is statistically improbable without some type of transposition, but that takes the entire message into consideration. I wonder if period 29/39 is statistically significant when taking into account the bottom half only. How does it compare to period 15/19 across the entire message? The pivots are almost entirely in the bottom half… still wondering about any possible relationship. There is something fishy about those darn period 29/39 repeats and the pivots.
Message coming within days, maybe sooner. I have been busy lately. I would be happy to make a more complicated one, but don’t want to keep you waiting.
O.k., Here is smokie33. There are 8 poly symbols with count of about 80 across the message. The plaintext is original. Cyclic substitution; no transposition.
21 46 1 35 10 33 2 50 11 14 30 26 6 27 39 57 51
23 40 34 15 33 4 10 16 54 4 7 41 52 19 47 61 22
48 42 58 54 13 5 17 18 20 59 28 55 24 8 49 57 53
25 14 14 14 15 10 43 16 44 45 17 46 55 14 54 54 52
55 18 23 47 62 56 23 6 38 9 39 48 38 54 40 49 55
26 31 30 1 51 27 35 6 41 14 35 42 28 31 19 14 30
11 26 34 34 14 12 26 2 56 14 6 62 60 24 16 36 13
3 33 23 20 48 61 58 37 54 27 32 51 6 28 21 25 55
32 62 8 47 6 52 43 57 14 48 61 14 38 44 4 45 16
49 56 40 33 14 6 53 23 26 32 6 54 2 8 41 54 59
27 55 23 22 48 42 57 54 14 21 14 15 19 9 14 1 46
50 14 30 61 52 24 47 17 13 12 18 13 6 25 14 14 10
2 48 7 23 15 16 52 17 8 24 39 23 44 18 10 49 14
12 40 35 27 40 36 9 25 42 44 45 17 10 56 42 33 3
54 39 4 37 14 53 23 14 16 10 11 17 10 46 18 13 31
14 2 20 32 15 55 54 58 7 16 57 54 17 47 16 14 23
48 18 50 38 41 23 16 43 43 18 49 51 60 6 54 24 21
14 17 18 38 56 1 6 14 52 2 57 7 14 56 25 17 35
3 6 54 16 14 38 1 56 17 29 54 32 1 45 18 37 41
53 33 26 56 23 47 14 10 54 2 9 39 52 3 57 6 15
I’ve been studying the 340. I see MR and WR as the same letters. The W is a mirror image of the M. Both have an R next to these to different letters( M & W).
@doranchak or anyone that’s interested.
I’ve given some thought to the normalization of the non-repeat measurement and came up with the idea that we can simply normalize by the maximum score a string can attain.
The give an example take this string "ABCDABCDA" it has 9 symbols total and 4 unique.
ABCDABCDA
————–
4444444321
The numbers are the lengths and sub scores for each starting point. So it seems to be a simple 2 part formula.
c=total symbols s=unique symbols score=non-repeat score of cipher max=c*s-s*(s-1)/2 new_score=score/max
Edit: simplified the calculation.
So now it returns a number between 0 and 1 telling us about the non-repeat score. It seems much better and intuitive to work with these new numbers. What do you think?
340 = 0.229
408 = 0.262
408 part 1 = 0.312
408 part 2 = 0.403
408 part 3 = 0.212
beale 1 = 0.110
beale 2 = 0.107
beale 3 = 0.107
Sum all its positions, divided by 24 will yield 171. In other words, the symbol is perfectly spread around the middle of the cipher.
I revisited this phenomenon, because I was curious about its statistical significance. So as usual, I ran a shuffle test:
1) Randomly shuffle the cipher
2) For each symbol, measure its spread
3) Repeat 1,000,000 times
4) Compute the min, max, mean, and std dev for the spread values for each symbol
5) For each symbol of the unmodified cipher, compare the actual spread to the average spread observed for shuffles.
Here are the results for Z340 and Z408: https://docs.google.com/spreadsheets/d/ … sp=sharing
Note the column marked “sigma”. For each cipher, higher sigmas are at the top and lower sigmas are at the bottom. You can see that some of Z340’s symbols such as “C” and “#” have high sigma because they are biased towards different halves of the cipher text.


And you can see that some of Z340’s symbols such as “+” and “H” have low sigma because they are well-balanced in the cipher text.


You can see similar qualities for Z408’s symbols. For example “_” is very biased towards the bottom half:

A few of Z408’s symbols have low sigma, too, but they aren’t nearly as high count as Z340’s “+” symbol.
I plotted Z340’s sigmas against Z408’s sigmas, each in descending order. The Z340 plot is slightly scaled so it occupies the same x-axis length as the Z408 plot, to give a general sense of how the symbol spread behaves with both ciphertexts:

Left side of the plot represents symbols that have higher sigma, meaning they are more significantly "unbalanced" in the cipher text compared to random shuffles. The red line corresponds to Z340, and the green line corresponds to Z408. You can see that the Z408 starts off with unbalanced symbols of higher significance. Then, its remaining symbols seem to behave similarly to Z340’s. This may suggest that the Z340’s symbols act a bit more randomly than Z408’s, which I think we already knew. But it is interesting to see it from this angle.
If we could find somebody like Ray, in the movie Rainman. He could solve this thing.
The 340 will drive me mad! I work on it almost every day.
Left side of the plot represents symbols that have higher sigma, meaning they are more significantly "unbalanced" in the cipher text compared to random shuffles. The red line corresponds to Z340, and the green line corresponds to Z408.
Thanks for running this test doranchak. How is the standard deviation calculated?
You can see that the Z408 starts off with unbalanced symbols of higher significance. Then, its remaining symbols seem to behave similarly to Z340’s. This may suggest that the Z340’s symbols act a bit more randomly than Z408’s, which I think we already knew.
So, symbols that have higher sigma are more unbalanced around its projected center. I came up with the idea of that test as another way of measuring one of the encoding properties of sequential homophonic substitution. Namely that the symbols in that case would have a lower sigma on average versus random encoding.
Take the following string "ABCABCABC". It is sequential and the symbols are well spread and therefor emits a lower sigma. "BCBAACACBC" is random and should emit a higher sigma because the spread is just not as good. What we already knew is that the 340 appears to be more random in its encoding than the 408, but that should give the 408 a lower sigma than the 340 and not the other way around.
I just took another look at the measurement. Loop all unique symbols, for each symbol sum its positions then divide them by frequency and subtract (ABS) this from the projected middle of the cipher (1+340)/2 and then multiply this number by the symbol frequency again to give appropriate weight to the observed distance. Divide the final number by the number of total symbols for normalization.
340: 22.65
408: 24.12
doranchak1: 35.81
doranchak2: 27.27
doranchak3: 34.71
doranchak4: 28.27
doranchak5: 29.14
doranchak6: 22.84
The 408 is higher while it should be lower. The value seems to go down as cyclic properties of the cipher improve.
Thanks for running this test doranchak. How is the standard deviation calculated?
It is computed by measuring symbol spread for each distinct symbol. The measurements are taken from 1,000,000 random shuffles, so there are 1,000,000 measurements per symbol. The standard deviation is directly computed from each of those collections of 1,000,000 measurements (it is the square root of the average of the squared differences of the values from their average value). Then, I look at a symbol’s actual spread in the unmodified Z340, which tells me how far it is from the mean. Dividing that absolute distance by the standard deviation gives me the sigma value.
I just took another look at the measurement. Loop all unique symbols, for each symbol sum its positions then divide them by frequency and subtract (ABS) this from the projected middle of the cipher (1+340)/2 and then multiply this number by the symbol frequency again to give appropriate weight to the observed distance. Divide the final number by the number of total symbols for normalization.
340: 22.65
408: 24.12
doranchak1: 35.81
doranchak2: 27.27
doranchak3: 34.71
doranchak4: 28.27
doranchak5: 29.14
doranchak6: 22.84The 408 is higher while it should be lower. The value seems to go down as cyclic properties of the cipher improve.
That sounds like it could be a good way to corroborate other measurements of cyclic behavior of unknown ciphers.
So now it returns a number between 0 and 1 telling us about the non-repeat score. It seems much better and intuitive to work with these new numbers. What do you think?
That seems useful for comparing ciphertexts of different lengths. Not sure what else to think about it. But, I did reproduce this measurement since it is easy to compute, so I’ve added it to my toolbox of measurements. Thanks!
Do you get a value of 0.17843556 for smokie33?