I have been thinking about a way to expand a multiple cycle symbol into one new symbol for each cycle, instead of one new symbol for each occurrence of the multiple cycle symbol. A segregated expansion instead of a full expansion. Like many cryptography techniques, it may not have perfect results. The goal is to find a "best guess" breakdown of, say 24 count symbol +, into symbols 64, 65, 66, and 67.
I have a very simple new spreadsheet suite that I can use to crudely hill climb a segregated expansion with cycles. I can select how many new symbols. The spreadsheet starts with a random segregation, then makes a few changes with each iteration. The cycle score spreadsheet compares each new symbol with every pre-existing symbol, but doesn’t’ compare new symbols with each other, or pre-existing symbols with each other.
There are eight such multiple cycle symbols in smokie33, which has cycles that are about 75% perfect on average. So far, I have been able to get an almost perfect segregation expansion with one of the symbols, an imperfect segregation with one other symbol, and mixed or not particularly good results with the other symbols. I am still exploring how best to score the cycles for this process.
Other concepts that I am thinking about are uses for the repeats.
Example 1
Let’s say we have repeats A+ A+ and B + B +, and we want to segregate + into 64, 65, 66 and 67. We could segregate by making A64 A64 and B65 B65. That might not be the correct segregation, because with A+ A+ the two +’s might not map to the same plaintext, and with B+ B+ the two +’s might not map to the same plaintext. But it is a guess. Now if you can do that and also find out that 64 cycles with X and 65 cycles with Y, then you have a better guess. And the higher the cycles scores, the better the guess, right?
Example 2
Now let’s say we have repeats A+ A+ and B+ B+, and we want to segregate + into 64, 65, 66 and 67. But we also know that A cycles with B and therefore could map to the same plaintext. We could segregate by making A64 A64 and B64 B64. That might not be the correct segregation, because cycle AB could be false. But it is a guess. The higher the cycle score for AB, the better the guess. If there is a conflict, such as where A cycles with B and A cycles with C, but B and C don’t cycle together, then it is not as good of a guess.
Example 3
Now let’s say we segregate the + into 64, 65, 66, and 67. And we get an unlikely perfect segregation. I doubt that could be achieved, but that would obviously be better than expanding the + into 24 new symbols. But what about 80% perfect segregation? Would that be better than 24 new symbols? Or what about 60% perfect segregation? Or what about describing segregation by saying that 64 and 65 are segregated perfectly, but 66 and 67 have mixed, imperfect segregations? That’s what I have been getting with my latest experiments on smokie33. There has to be a point where full expansion is as good as a segregated expansion. Where they have equal usefulness for solving purposes. EDIT: Perhaps merge mixed, imperfectly segregated 66 and 67 back together for further testing, new segregation expansion, or even full expansion.
Anyway, I have been wanting to work on these concepts for several months now. It’s my next project. I am going to work on it in small chunks, and take breaks and think about it, and work in more small chunks. I hope to at least make a basic exploration.
Another topic:
I added a new website to the CRYPTOGRAPHY WEBSITES page. The University of Mainz in Germany apparently teaches some cryptography courses and has an extensive outline available online. I think that you guys might be interested in perusing the 261 pages. Check out pages 175 – 177. It seems as though the authors are talking about scoring bigrams when solving different transposition messages. I thought that was interesting.
http://www.staff.uni-mainz.de/pommeren/ … lassic.pdf
Your symbol segregation idea is very interesting. I think an imperfect segregation is better than nothing, so it makes sense to explore in that direction since the set of all possible symbol expansions is quite large. Even if you limit the expansion of the 24 "+" symbols into only one additional symbol besides "+", there are still 2^24 = over 16 million possible assignments of those symbols to explore. Not too bad, but that number goes up fast as the number of segregated group per symbol goes up.
Thank for posting the new crypto resource – lots of very good stuff in that PDF. I look forward to reading it.
I currently am feeling very positive about the 340, and think that with our most recent discoveries, someone may solve it.
I was also thinking about a recent conversation where we were talking about how maybe Zodiac used different types of transposition schemes for different parts of the message. That got me to thinking about the highly improbable <S period 19 repeats.
If the Zodiac 340 isn’t a transposition message, then the original plaintext would have had a lot of period 19 repeats before encoding, and also a lower count of period 1 repeats before encoding. Still then, with 63 symbols, he would have had to diffuse the period 19 plaintext inefficiently, and diffuse the period 1 plaintext efficiently.
So back to the improbable <S repeats, which I call symbols 29 and 42. Note that they occur in the bottom half of the message, where we also have a high density of period 29 / 39 repeats. One would think that these highly improbable repeats would occur in the top half of the message, where symbol skips, nulls, or whatever else, is disrupting period 19 repeats and causing the period 29 / 39 repeats. But they don’t.
However, perhaps a look at where highly improbable repeats, whether 15, 19, 29, or 39, occur, can help us to determine if Zodiac used one transposition scheme across the entire message, or multiple transposition schemes in different parts of the message. . . . or perhaps we could consider different keys for different parts of the message.
.
It may be worthwhile to conduct a study of exactly how improbable the "regional" biases actually are. I.e., scramble the cipher a bunch of times and see how often the transposed repeats appear in regional clusters. Similar to these studies of the period 1 repeats (top vs bottom half, and even vs odd positions): http://zodiackillerciphers.com/wiki/ind … am_repeats
Do you get a value of 0.17843556 for smokie33?
Yes.
If the Zodiac 340 isn’t a transposition message, then the original plaintext would have had a lot of period 19 repeats before encoding, and also a lower count of period 1 repeats before encoding. Still then, with 63 symbols, he would have had to diffuse the period 19 plaintext inefficiently, and diffuse the period 1 plaintext efficiently.
I have thought exact the same thing. Your wildcard segregation idea looks nice, let me know if you want a test cipher.
Your wildcard segregation idea looks nice, let me know if you want a test cipher.
O.k. I will. I work on the 340 in cycles much how Zodiac cycled through his homophonic ciphertext groups . . . . ![]() . . . . but right now I am in first or second gear. I may develop the system with my own messages and then ask.
. . . . but right now I am in first or second gear. I may develop the system with my own messages and then ask.
I was also thinking about a recent conversation where we were talking about how maybe Zodiac used different types of transposition schemes for different parts of the message.
Do you think that its possible the localities could overlap?
Soze
I can’t do it today but, unless otherwise stated, I will post the example tomorrow.
Soze
I was also thinking about a recent conversation where we were talking about how maybe Zodiac used different types of transposition schemes for different parts of the message.
Do you think that its possible the localities could overlap?
Soze
Maybe, if there are multiple transposition schemes, they could overlap. I think that it would be very difficult to figure out, even with some creative thinking. I will put it on my to do list to examine the locations of the most improbable period 15/19 and 29/39 repeats. That would be a good start.
Your wildcard segregation idea looks nice, let me know if you want a test cipher.
O.k. I will. I work on the 340 in cycles much how Zodiac cycled through his homophonic ciphertext groups . . . .
. . . . but right now I am in first or second gear. I may develop the system with my own messages and then ask.
Nice to hear that you are doing so well. I seem to performing better than average myself, perhaps it’s a seasonal thing?
Mainly working on AZdecrypt while letting the wildcard test run on my other machine. I don’t want to say to much about the new version of AZdecrypt I’m working on but it’s looking very, very good. Partially redesigned the algorithm and my new ideas have been paying off big time. It runs at least 33% faster and the solve rates have been improved, the 408 for instance now solves 85% of the time at 500k iterations.
One other thing that I came up with while creating the anagram solver was to wrap around the cipher. In allot of cases it makes sense to do this and so I’ve added it to substitution solver as well.
Imagine a short cipher and count the times each letter is scored (observations) while the n-gram scoring mechanism slides through the cipher. Let’s say 6-grams for this example.
ABCDEFGHIJKLMNOPQRST -------------------- 12345666666666654321
The amount of information that is captured by the n-grams is equal to the total sum of observations. This gives 90. Now wrap around the back of the cipher.
ABCDEFGHIJKLMNOPQRST -------------------- 66666666666666666666
This gives 120, a 33% increase of information. Now alternatively you could fill in these bits with lower level n-grams but then you’d have to include them every time the program loads and it would slow down and complicate the algorithm much more than the wrapping process, which can simply be done by extending the cipher.
I’m looking forward to the new version, Jarlve! So glad you are back working on this. Thanks!
I have been working on segregation, slowly but surely. Working on identifying certain period x repeat situations and how to score them, in conjunction with cycle scores, to hill climb a close segregation. I am currently working on situations where a new segregated symbol position is a member of multiple period 1-5 repeats
I am so far not successful at using period x repeats to hill climb segregation of poly symbols, at least with smokie33 and situations where a new segregated symbol position is a member of multiple period 1-5 repeats. I can make a message with perfect segregation of a symbol, and then make a few random changes. And it is easy to improve the period repeat scores far above the perfect segregation period repeat scores with the new, incorrect segregation.
I am currently working with the cycles, and think that they are the best chance. Smokie33 is not as cyclic as the 340, especially in the 2nd half of the message, and so this message is very difficult. However, I was able to get a decent segregation of symbol 23.
I spent yesterday making a new souped up cycle spreadsheet with cleaner, more concise formulas and better efficiency. I haven’t looked closely at the cycles in a long time. The 340 is very cyclic. I did some shuffle tests, and most of the high scoring cycles in the 340 are real. Now, with all of this time to learn more about aspects of the 340 and different techniques for analyzing similar messages, my interest in the cycles is renewed. Perhaps working with segregation will help.
I have spent a lot of time this last week on segregation, and am disappointed to say that it is not working out. I made a message with one poly symbol that was a member of four cycle groups, and almost identical cycle stats to the 340. I found out that it is easy to hill climb an incorrect segregation with a much higher score than a perfect segregation. I got about 2/3 of the symbols correct. But with my poly symbol, which has count of 23, there were other ways to create very high scoring cycles rather than the correct segregation. But I was using the exponential formulas to calculate cycle scores. I may try with log10 of the exponential scores.
Great timing, smokie – as it turns out, I’ve been looking rather closely at the cycles in the last few days.
Sorry your segregation tests are not working out. At the least, the negative result still serves as a useful data point in your efforts.
I, too, ran some shuffle tests. My goal was to try to estimate the significance of sequential cycle patterns in Z340, Z408 and smokie33 in more detail.
First, some terminology:
- Cycle: Pattern of symbols that repeat in some orderly pattern. Example: ABC ABC AB ABC <== cycle is “ABC”
- L: Number of symbols in the cycle . Example: L=3 for the cycle ABC.
- Run: The number of times the cycle repeats perfectly without interruption. Example: The full sequence ABC ABC ABC AB ABC has a run of 3 for the cycle ABC.
- perfectCycle: My weighted sum of runs detected over all cycles. This measurement is taken for L=2, 3, and 4.
- jarlveCycle: This is Jarlve’s m_2s_cycles score, a count of cycles found for L=2.
- nonrepeat: Jarlve’s nonrepeat score, which tends to be higher for ciphers that have a lot of cycling.
- nonrepeatAlternate: Jarlve’s alternate nonrepeat score. Lower scores indicate more cycling.
- nonrepeatAlternateNormalized: Normalized nonrepeat score. Converts the nonrepeat score to a value between 0 and 1.
- min: This is the minimum value the measurement found across all shuffles.
- max: This is the maximum value the meaurement found across all shuffles.
- mean: This is the average value found across all shuffles.
- std dev: This is the standard deviation found across all shuffles.
- actual: This is the measurement for the actual (unshuffled) cipher text
- sigma: This is the number of standard deviations between the actual measurement and the average of the shuffles. Higher sigma means more significance.
- cipher: Which cipher text was tested
- alphabet length: The number of unique symbols in the cipher’s alphabet
- cycle length: The value of L tested
- combinations: The total number of possible combinations of L symbols taken from the cipher alphabet. For example, Z340’s alphabet has 63 symbols, and the number of ways to take 3 symbols from it is: (63 choose 3) = 39,711
- runs: The run value
- count: The number of different cycles that had this run value
- count/combinations: The ratio of cycles with this count, to the total number of possible cycles
- symbols: The symbols in this particular cycle
- length: How many times each symbol appears in the cipher text
- min: Lowest run value found for this cycle during all the shuffles
- max: Largest run value found for this cycle during all the shuffles
- mean: Average run value for this cycle during all the shuffles
- std dev: Standard deviation of the run value for this cycle during all the shuffles
- actual run: The actual run value from the unmodified (unshuffled) cipher text.
- sigma: Number of standard deviations the actual run value is from the shuffle average
- 3025 shuffles had run=1
- 4984 shuffles had run=2
- 1504 shuffles had run=3
- 369 shuffles had run=4
- 94 shuffles had run=5
- 17 shuffles had run=6
- 7 shuffles had run=7
[/list:u:1fy8fkze]
For each cipher, I ran 10,000 shuffle tests for L=2 and L=3. Because L=4 takes a long time, I limited it to 1,000 shuffles.
Here’s the spreadsheet with all my data: https://docs.google.com/spreadsheets/d/ … sp=sharing
The first cycle measurements I looked at were the “overall” measurements that reflect how well the ciphers cycle overall. These include:
[/list:u:1fy8fkze]
The results are in the first tab in my spreadsheet: https://docs.google.com/spreadsheets/d/ … sp=sharing
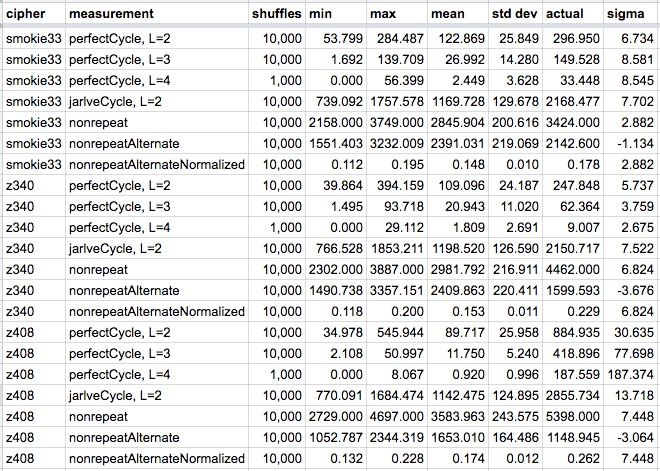
Here are the values for each measurement:
[/list:u:1fy8fkze]
Generally speaking, the results show that across all measurements, Z408’s cycle measurements are the most significant. Smokie33’s are the next most significant, and Z340’s are the least significant. However, Z340’s measurements are still well beyond shuffle averages. In particular, four of its measurements are 5 sigma or more away from the shuffle mean.
Here is another interesting observation. Look at the values for “perfectCycle” for L=2, 3, and 4 for each of the cipher. For smokie33, sigma is 6.7 for L=2, then goes up to 8.6 for L=3 and stays at 8.5 for L=4. For Z408, sigma is 30.6 for L=2, then more than doubles to 77.7 for L=3, and leaps to 187.4 for L=4. However, for Z340, sigma is 5.7 for L=2 and then drops significantly to 3.8 for L=3 and 2.7 for L=4. Perhaps whatever is screwing with ngram repeats has this suppressing effect on cycling as L increases.
It is also worth noting how extreme the significance (sigma) is for Z408. The measurement for perfectCycle (L=4) has a sigma of 187.4. This means that it is more than 187 standard deviations from the mean observed during the shuffles. If the measurement has a normal distribution, then accoring to this calculator the chance of this happening purely at random is 1 in 4.8 x 10^7627, a staggeringly large number.
Compare that to Z340’s perfectCycle measurement for L=4. It has a sigmal of only 2.7, which has a 1 out of 267 chance of happening completely at random. Big difference! Still, it shows great significance for perfectCycle at L=2, which has a sigma of 5.7. That corresponds to a 1 in 207,000,000 chance of happening at random.
Next, I look at overall cycles found that had runs of 2 or higher in the unmodified ciphers. The number of cycles is then compared to the number of all possible cycles. Results are in the spreadsheet tab labelled “Cycle run counts”. Each result shows:
[/list:u:1fy8fkze]
For example, for L=2, Z408 has 1143 cycles that have run values of 2 or higher. Z408 has only 1431 different cycles to pick from in the first place, meaning that about 80% of the cycles show at least one uninterrupted repetition.
The results tell a similar story: Z408 has the most significant cycling, Z340 has the least, and smokie33 is a bit more significant than Z340.
The remaining tabs in the spreadsheet break down the shuffle experiments by individual cycles.
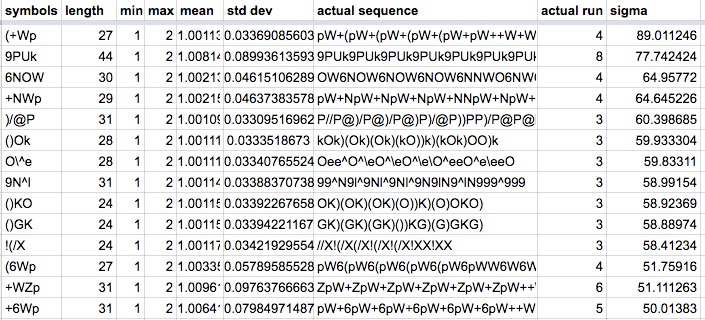
Here’s what the headings mean:
[/list:u:1fy8fkze]
For example, for Z340 and L=4, the most significant cycle involves symbols "-<By”, which produces a run of 3 in this full sequence: B <By- <By- <By- B<ByByB-B<B<BB-. A run of 3 was found to be 58.5 standard deviations away from the average run observed for this cycle during shuffles.
One thing that was kind of surprising was the top two L=3 cycles for Z340. The most significant was “%cj” which has run=2 in the full sequence “%cj %cj cccccccc”. “JMc” is less significant, but has a higher run of 4 in the full sequence “cM JMc JMc JMc JMc ccMcccM”. I think the reason “%cj” is more significant is because there are 10 c’s, but only 2 %’s and 2 j’s, which makes it harder for the unbroken pattern to appear by chance.
I’m not sure if the distribution of measurements for shuffled ciphers is truly normal, which is an assumption I’ve been making in this analysis. For instance, for L=2 for Z340, the most significant cycle is “Ml" which has a perfect run of 7 in the full sequence “lMlMlMlMlMlMlM”. This gives it a sigma of of 5.9. For a normal distribution, there’s a 1 in 570 million chance of randomly picking a shuffled cipher that has such a high sigma. But, in practice, I found these counts per run for “Ml” in the 10,000 shuffles of Z340:
[/list:u:1fy8fkze]
So, 7 in 10,000 (about 1 in 1,400) had a perfect run of 7 completely by random chance. That is much more probable than 1 in 570 million! So maybe the distribution isn’t normal, or my calculations have some mistake.
I should revisit this analysis after I brush up on more statistics fundamentals! ![]()
Wow, thanks for the in-depth analysis.
I’m not sure if the distribution of measurements for shuffled ciphers is truly normal, which is an assumption I’ve been making in this analysis.
I was wondering this myself. See page 16 of this thread:
I have been doing some testing on my own. To answer the question in my mind about randomization and cycles. I have been showing quantities of certain cycle lengths in prior posts. Statistics about how many ABABAB cycles are in the 340, etc. And I have randomly scrambled the 340 in its entirety to compare with the 340 cycle statistics to determine about how many of the cycles in the 340 are true or false. My question was whether, if I make a message with about the same number of high, medium and low count symbols, and select the symbols at random, will the statistics be comparable to the statistics for a randomly scrambled 340?
The answer to that question is yes. I will post the stats a bit later. And another question. What degree of randomization did Zodiac use with the 340. The answer is More than 20% and less than 35%. About 25% to maybe 30%. And I will post stats a bit later.
The next question is, does the apparent random symbol selection have anything to do with why the 340 cannot be solved? Is that evidence of the second step? He did that to some degree with the 408, and it solves fine. So, is there a relationship between apparent random symbol selection and the reason whey the 340 has not yet been solved?
And a few posts below that, I made some messages with 100% random symbol selection all homophonic. I didn’t cycle the symbols. And I found out that the stats were practically the same as if you shuffle the 340.
I did a little intra-cycle random symbol analysis to figure out just how much Zodiac may have selected his cycle symbols at random. I used the first 340 of the 408 and made a key to approximately match the 340 distribution of symbol count:
test 1 key:
A 1 36
B 5
C 6 7
D 8 9
E 10 11 12 13 14 15 16
F 18
G 19 20 52
H 21 22 23 24 2 4
I 25 26 27 28 29 37
J
K 30
L 31 32 33
M 34
N 35
O 39 40 41 42 43
P 44 45 3
Q
R 46 47 48
S 49 50
T 53 54 55 56 57 38
U 59 60 51
V 61
W 62 63
X 17
Y 58
Ztest 1 total number of symbols in left column, count per symbol in right column. For example, there are twelve symbols with a count of 4.
1 1
9 2
5 3
12 4
10 5
9 6
7 7
1 8
3 9
2 10
2 11
0 12
1 13
1 21random.stats.png
random.stats.png (26.47 KiB) Viewed 51 times1. Every column except A is the mean number of cycles over ten randomizations.
2. Comparing A and B, we see what we already know, that Zodiac used cycles because the 340 has more cycles than if we completely scramble the 340.
3. Compare B and C. I made ten test 1 messages with 100% random symbol selection. The closeness of the numbers shows that there is little if any difference between scrambling a message and using 100% random symbol selection when making a comparison to the actual 340 cycle stats.
4. Compare A with D through H. The numbers show that Zodiac used intra-cycle randomization of about 25% – 30%. It’s kind of tough to draw an exact number. But with only 20% randomization, there are going to be some cycles that score higher than with the 340. With 35% to 40% randomization, there are generally not as many high scoring cycles.
See: viewtopic.php?f=81&t=2617&start=150
I am going to look at the cycles again, for a little while. I needed a break from transposition anyway.
Your analysis is a lot to chew, so I appreciate the interpretation. That helps a lot. Today I was thinking about what you call "regional bias." I was wondering if there may be one group of unbroken cycles, say ABABAB that have one regional bias, and another group of unbroken cycles, say CDCDCD that have another regional bias. As if he used a different key for the top versus the bottom, etc.
More than likely I have already said that before and can’t remember or find it on this thread. But with my new cycle spreadsheet, I can take a look.
The log10 scoring approach for segregation didn’t work. Another week spent on a fruitless experiment, but at least I know more than I did before!


