Thanks for linking to your previous study. It is useful to see that random cycles have very similar stats to full shuffles. It seems that the individual cycle sequences in Z340 have a relatively high probability of occurring strictly by chance, but for so many cycles to do so seems very improbable.
If we are lucky, the disruption in cyclic symbol assignment is directly connected somehow to the additional steps that may have been applied to the plaintext.
I’m interested to see what you come up with about the regional bias question for cycles.
Thanks for linking to your previous study. It is useful to see that random cycles have very similar stats to full shuffles. It seems that the individual cycle sequences in Z340 have a relatively high probability of occurring strictly by chance, but for so many cycles to do so seems very improbable.
If we are lucky, the disruption in cyclic symbol assignment is directly connected somehow to the additional steps that may have been applied to the plaintext.
I’m interested to see what you come up with about the regional bias question for cycles.
Wouldn’t you have to have a cycle in the plaintext to get a false homophonic cycle in the ciphertext? Am I thinking right?
They would probably be mostly random and with not very many consecutive alternations. But don’t some letters naturally occur before other letters in common words or word orders ( T comes before H and E)? I am just wondering if a study of naturally occurring plaintext cycles, including particular letters, count of consecutive alternations, frequency, and actual distance ( consider T, H and E) between high frequency letters would help us to guess if a ciphertext cycle is true or false.
For example, a two ciphertext cycle with a few consecutive alternations, and where two positions are close to each other, may be caused by a repeated phrase. Not taking transposition into consideration.
I am not really sure if a transposition, performed before encoding, would affect cycles. Except that it would destroy the plaintext cycles that occurred before transposition, and create plaintext cycles.
Yes, it makes more sense that the disruption would be because of a post-encipherment step.
Also, a falsely detected homophone cycle does not necessarily reflect the conditions of the plaintext, since the symbols in the false cycle don’t necessarily stand for the same letter. They could be anything. I don’t think the cycle would need to exist in the plaintext. Maybe it would help to dig up some sample false cycles from Z408 and other test ciphers.
I think that a good exercise would be to find randomly occurring cycles in a plaintext sample. Then cycle encode with 63 symbols. Find the false cycles in the message. Then compare to the originally found randomly occurring false cycles in the plaintext sample.
Thanks for your massive analysis doranchak, I like it allot!
Here is another interesting observation. Look at the values for “perfectCycle” for L=2, 3, and 4 for each of the cipher. For smokie33, sigma is 6.7 for L=2, then goes up to 8.6 for L=3 and stays at 8.5 for L=4. For Z408, sigma is 30.6 for L=2, then more than doubles to 77.7 for L=3, and leaps to 187.4 for L=4. However, for Z340, sigma is 5.7 for L=2 and then drops significantly to 3.8 for L=3 and 2.7 for L=4. Perhaps whatever is screwing with ngram repeats has this suppressing effect on cycling as L increases.
That’s extremely interesting. Smokie and I have found the 340 to be "very cyclic" but both of us have mainly looked at 2 symbol cycles. It is also interesting to note that smokie’s wildcard scheme has the effect of suppressing the non-repeat score. That seems not to be happening for the 340. As a reminder there is strong peak for the non-repeating string frequencies at 17. And empirically, I found that it’s hard to mix that observation with randomization of cycles or transposition after encoding.
I have just ran a 3 symbol cycle test and found the 340 to be further away from the randomized average than with 2 symbol cycles but my test may be flawed. That aside let’s assume that the higher symbol cycles are indeed more suppressed. Because that is what is shown relative to the smokie33.
Wildly brainstorming, just want to throw some rough ideas around.
– Prior to the homophonic substitution an encryption was used that redistributed the letters over a large number of symbols. Let’s say 40 or so, meaning that not many 3 to 4 symbol cycles had to be used.
– Something intentionally was applied to the higher symbol cycles to mask them.
– Some kind of polyalphabetism thrown into the mix.
340 versus AZdecrypt:
A particular test I wanted to run, and also to test the solving routine of the new and upcoming AZdecrypt. It now automatically normalizes the scores of the n-gram files so that on average, ciphers score the same. The 340’s score of 20351 with the Practical Cryptography 5-grams has been kept. So for this test, the normal 340 is scored (maxed out) with 6 different sets of n-grams and 2 different plaintext normalizations, namely the index of coincidence and entropy.
Notice that the 340’s plaintext solution is a dominant theme with almost all results, I still wonder if that is to be expected. I think that ZKDecrypto also converges on this theme. Also notice that the scores go down as the n-gram size goes up, while I previously stated n-gram score normalization. This is because the solver cannot find a good fit and thus lower scoring less-frequent n-grams have to be used. And when the n-gram size goes up, from 5 to 6 and 7, the fit becomes increasingly worse if the cipher somehow is not as expected.
Index of coincidence:
AZdecrypt 0.993 (Practical Cryptography 5-grams) Score: 20351.27 Ioc: 0.07520389 Entropy: 3.919787 Characters: 340 Letters: 20 gshiscentopernatm estelsilarldeiavo edvantocarlorsegi nsspectingsitthat sunterimporttheof sthercisimporital sotablytoacanderp lativisitseletoru mentatchtreadysea seconteitispereds othforspalesannai teachipionendther esundsteporealyth careevoteadanertt deceiveupsinocost padgeealisedvnbat hantrespetrcrepor ttorperatingnflos promrepreslieispa inagesonecitypayt Multiplicity: 0.1852941 Symbols: 63 Bigrams: 25 Flatness: 0.7331541 Sequential: 0.2292084 HER>pl^VPk|1LTG2d Np+B(#O%DWY.<*Kf) By:cM+UZGW()L#zHJ Spp7^l8*V3pO++RK2 _9M+ztjd|5FP+&4k/ p8R^FlO-*dCkF>2D( #5+Kq%;2UcXGV.zL| (G2Jfj#O+_NYz+@L9 d<M+b+ZR2FBcyA64K -zlUV+^J+Op7<FBy- U+R/5tE|DYBpbTMKO 2<clRJ|*5T4M.+&BF z69Sy#+N|5FBc(;8R lGFN^f524b.cV4t++ yBX1*:49CE>VUZ5-+ |c.3zBK(Op^.fMqG2 RcT+L16C<+FlWB|)L ++)WCzWcPOSHT/()p |FkdW<7tB_YOB*-Cc >MDHNpkSzZO8A|K;+ AZdecrypt 0.993 (Reddit corpus 5-grams) Score: 20650.56 Ioc: 0.06810689 Entropy: 4.020609 Characters: 340 Letters: 21 glhystundeconsedp ostersiformnoiate edcasticerrensogi nssbuttingsitthad mastolipcardtheep sthurtiliplerydor satawfudiavennonc reditisitmomotina postitchdreadywea lotintuitisboredl ithpallcomesissai doathiciasesnther owandstocarearuth teroutadeinaneltt devoiceallynicalt cangoearisuntswed hastnowlotrtrecen tterloradingspres creproblemmieilla ysogosenocitycaut Multiplicity: 0.1852941 Symbols: 63 Bigrams: 25 Flatness: 0.7331541 Sequential: 0.2292084 HER>pl^VPk|1LTG2d Np+B(#O%DWY.<*Kf) By:cM+UZGW()L#zHJ Spp7^l8*V3pO++RK2 _9M+ztjd|5FP+&4k/ p8R^FlO-*dCkF>2D( #5+Kq%;2UcXGV.zL| (G2Jfj#O+_NYz+@L9 d<M+b+ZR2FBcyA64K -zlUV+^J+Op7<FBy- U+R/5tE|DYBpbTMKO 2<clRJ|*5T4M.+&BF z69Sy#+N|5FBc(;8R lGFN^f524b.cV4t++ yBX1*:49CE>VUZ5-+ |c.3zBK(Op^.fMqG2 RcT+L16C<+FlWB|)L ++)WCzWcPOSHT/()p |FkdW<7tB_YOB*-Cc >MDHNpkSzZO8A|K;+ AZdecrypt 0.993 (Usenet corpus 6-grams) Score: 17804.07 Ioc: 0.07766788 Entropy: 3.867273 Characters: 340 Letters: 19 gahsscentoplanotm ustersilorsdeiane edmantocorreasegi nsspectingsitthat sinterimporttheoe sthercisimworstor sotablytoacondeap rotinisitsusethai mentatchtreadylea seconteitispereds otheoraposesannai teachipionendther elindstuporearyth coruenoteadanertt declimeiwasnocost padgeearisednnbot hantallwetrcrepea tterweratingneres promrepressieiswa snogusonecitypayt Multiplicity: 0.1852941 Symbols: 63 Bigrams: 25 Flatness: 0.7331541 Sequential: 0.2292084 HER>pl^VPk|1LTG2d Np+B(#O%DWY.<*Kf) By:cM+UZGW()L#zHJ Spp7^l8*V3pO++RK2 _9M+ztjd|5FP+&4k/ p8R^FlO-*dCkF>2D( #5+Kq%;2UcXGV.zL| (G2Jfj#O+_NYz+@L9 d<M+b+ZR2FBcyA64K -zlUV+^J+Op7<FBy- U+R/5tE|DYBpbTMKO 2<clRJ|*5T4M.+&BF z69Sy#+N|5FBc(;8R lGFN^f524b.cV4t++ yBX1*:49CE>VUZ5-+ |c.3zBK(Op^.fMqG2 RcT+L16C<+FlWB|)L ++)WCzWcPOSHT/()p |FkdW<7tB_YOB*-Cc >MDHNpkSzZO8A|K;+ AZdecrypt 0.993 (Reddit corpus 6-grams) Score: 17836.36 Ioc: 0.07860489 Entropy: 3.848518 Characters: 340 Letters: 20 gdhiscantopernotm estersilarlsoiamo edvastocorrorsegu nssmactingsitthat wastenimparttheoe stharcinimnoritar satabletoaconserp rotumisitweletora mostitchtreadydea necontautismoredn otheandpalesinsai toachupianessther edandstepareareth coreamateisanentt deceiveandinocant pasgeearisasmsbot hantrednotrcrepor ttorneratingneros promromnewlieinna isagesonecitypaet Multiplicity: 0.1852941 Symbols: 63 Bigrams: 25 Flatness: 0.7331541 Sequential: 0.2292084 HER>pl^VPk|1LTG2d Np+B(#O%DWY.<*Kf) By:cM+UZGW()L#zHJ Spp7^l8*V3pO++RK2 _9M+ztjd|5FP+&4k/ p8R^FlO-*dCkF>2D( #5+Kq%;2UcXGV.zL| (G2Jfj#O+_NYz+@L9 d<M+b+ZR2FBcyA64K -zlUV+^J+Op7<FBy- U+R/5tE|DYBpbTMKO 2<clRJ|*5T4M.+&BF z69Sy#+N|5FBc(;8R lGFN^f524b.cV4t++ yBX1*:49CE>VUZ5-+ |c.3zBK(Op^.fMqG2 RcT+L16C<+FlWB|)L ++)WCzWcPOSHT/()p |FkdW<7tB_YOB*-Cc >MDHNpkSzZO8A|K;+ AZdecrypt 0.993 (Usenet corpus 7-grams) Score: 14542.63 Ioc: 0.08578865 Entropy: 3.731695 Characters: 340 Letters: 18 gdhsscentopornotd estersilarlseaamo edhastocorrorsegi nsspectantsitthat wastenedparttheoe sthercinaddorstar satabletoaconserp rotimesitweletgra destitchtreadylea neconteitisperedn otheandpalesinsai teachipaanessther elandstepareareth coreemateisanentt decoaheaddsnocant pasteearisesmsbot hantroldetrcrepor ttorderatingneros prodrepnewlieanda ssagesonecitypaet Multiplicity: 0.1852941 Symbols: 63 Bigrams: 25 Flatness: 0.7331541 Sequential: 0.2292084 HER>pl^VPk|1LTG2d Np+B(#O%DWY.<*Kf) By:cM+UZGW()L#zHJ Spp7^l8*V3pO++RK2 _9M+ztjd|5FP+&4k/ p8R^FlO-*dCkF>2D( #5+Kq%;2UcXGV.zL| (G2Jfj#O+_NYz+@L9 d<M+b+ZR2FBcyA64K -zlUV+^J+Op7<FBy- U+R/5tE|DYBpbTMKO 2<clRJ|*5T4M.+&BF z69Sy#+N|5FBc(;8R lGFN^f524b.cV4t++ yBX1*:49CE>VUZ5-+ |c.3zBK(Op^.fMqG2 RcT+L16C<+FlWB|)L ++)WCzWcPOSHT/()p |FkdW<7tB_YOB*-Cc >MDHNpkSzZO8A|K;+ AZdecrypt 0.993 (Reddit corpus 7-grams) Score: 14631.92 Ioc: 0.09003991 Entropy: 3.637693 Characters: 340 Letters: 16 iiestsinmeforlutn ettendonarmseasto eshastoturnordois ntthishandtottest hastoconfirmtheel theirsonanderstan ditsandtoagunsorf nutstodothemotora nestattetreasures nosontistotheresn otelicifametalsso teasesfailessther oransdtefireandhe sureititeasanectt segoaheadisnotint fasdoesnotistsaut ealtrordetrsrefor ttordoramonillnot frenrehcehmoeanda ssaietenotohufsdt Multiplicity: 0.1852941 Symbols: 63 Bigrams: 25 Flatness: 0.7331541 Sequential: 0.2292084 HER>pl^VPk|1LTG2d Np+B(#O%DWY.<*Kf) By:cM+UZGW()L#zHJ Spp7^l8*V3pO++RK2 _9M+ztjd|5FP+&4k/ p8R^FlO-*dCkF>2D( #5+Kq%;2UcXGV.zL| (G2Jfj#O+_NYz+@L9 d<M+b+ZR2FBcyA64K -zlUV+^J+Op7<FBy- U+R/5tE|DYBpbTMKO 2<clRJ|*5T4M.+&BF z69Sy#+N|5FBc(;8R lGFN^f524b.cV4t++ yBX1*:49CE>VUZ5-+ |c.3zBK(Op^.fMqG2 RcT+L16C<+FlWB|)L ++)WCzWcPOSHT/()p |FkdW<7tB_YOB*-Cc >MDHNpkSzZO8A|K;+
Entropy:
AZdecrypt 0.993 (Practical Cryptography 5-grams) Score: 20365.06 Ioc: 0.07515183 Entropy: 3.980048 Characters: 340 Letters: 22 gohiscentofurnatm estelsikarrdeiave edlantocarlersegi nsspectingsitthat wanterimforttheob sthercisimporital sotackstoabanderf lativisitweretura mentatchtreadymea seconteitispereds othborofaresannai teachifionendther emandsteforealsth careevoteadanertt debuileapoinocost fadgeealisedvncat hantrumpetrcrefer tterperatingnbles fromreprewrieispa inagesonecityfast Multiplicity: 0.1852941 Symbols: 63 Bigrams: 25 Flatness: 0.7331541 Sequential: 0.2292084 HER>pl^VPk|1LTG2d Np+B(#O%DWY.<*Kf) By:cM+UZGW()L#zHJ Spp7^l8*V3pO++RK2 _9M+ztjd|5FP+&4k/ p8R^FlO-*dCkF>2D( #5+Kq%;2UcXGV.zL| (G2Jfj#O+_NYz+@L9 d<M+b+ZR2FBcyA64K -zlUV+^J+Op7<FBy- U+R/5tE|DYBpbTMKO 2<clRJ|*5T4M.+&BF z69Sy#+N|5FBc(;8R lGFN^f524b.cV4t++ yBX1*:49CE>VUZ5-+ |c.3zBK(Op^.fMqG2 RcT+L16C<+FlWB|)L ++)WCzWcPOSHT/()p |FkdW<7tB_YOB*-Cc >MDHNpkSzZO8A|K;+ AZdecrypt 0.993 (Reddit corpus 5-grams) Score: 20589.14 Ioc: 0.07188964 Entropy: 4.008175 Characters: 340 Letters: 22 gohiscandoflenotm estendilarvsoiape edkastocorneedegu nssmactingsitthat wastenimfordtheoi stharcisimporitan dotablytoalonseef notupiditwevethea mostitchtreadylea secontautismoreds othionofavesinsai toachufionessther elanddteforeanyth coreapoteisanentt dellikeapoinocost fasgeeanisaspsbot hantellpotrcrefee tterperadingnines fromromnewvieispa isagesonecityfayt Multiplicity: 0.1852941 Symbols: 63 Bigrams: 25 Flatness: 0.7331541 Sequential: 0.2292084 HER>pl^VPk|1LTG2d Np+B(#O%DWY.<*Kf) By:cM+UZGW()L#zHJ Spp7^l8*V3pO++RK2 _9M+ztjd|5FP+&4k/ p8R^FlO-*dCkF>2D( #5+Kq%;2UcXGV.zL| (G2Jfj#O+_NYz+@L9 d<M+b+ZR2FBcyA64K -zlUV+^J+Op7<FBy- U+R/5tE|DYBpbTMKO 2<clRJ|*5T4M.+&BF z69Sy#+N|5FBc(;8R lGFN^f524b.cV4t++ yBX1*:49CE>VUZ5-+ |c.3zBK(Op^.fMqG2 RcT+L16C<+FlWB|)L ++)WCzWcPOSHT/()p |FkdW<7tB_YOB*-Cc >MDHNpkSzZO8A|K;+ AZdecrypt 0.993 (Usenet corpus 6-grams) Score: 17814.52 Ioc: 0.08351553 Entropy: 3.838646 Characters: 340 Letters: 21 gahsscentoplanots ustersilorsdeiame edfantocorreasegi nsspectingsitthat sinteresparttheoe sthercitisworstor satabletoacondeap rotimesitsusethai sentatchtreadykea teconteitisperedt othearaposesannai teachipianendther ekindstupareareth coruemateadanertt declifeiwasnocatt padgeearisedmnbot hantalkwetrcrepea tterweratingneres prosrepressieitwa snogusonecitypaet Multiplicity: 0.1852941 Symbols: 63 Bigrams: 25 Flatness: 0.7331541 Sequential: 0.2292084 HER>pl^VPk|1LTG2d Np+B(#O%DWY.<*Kf) By:cM+UZGW()L#zHJ Spp7^l8*V3pO++RK2 _9M+ztjd|5FP+&4k/ p8R^FlO-*dCkF>2D( #5+Kq%;2UcXGV.zL| (G2Jfj#O+_NYz+@L9 d<M+b+ZR2FBcyA64K -zlUV+^J+Op7<FBy- U+R/5tE|DYBpbTMKO 2<clRJ|*5T4M.+&BF z69Sy#+N|5FBc(;8R lGFN^f524b.cV4t++ yBX1*:49CE>VUZ5-+ |c.3zBK(Op^.fMqG2 RcT+L16C<+FlWB|)L ++)WCzWcPOSHT/()p |FkdW<7tB_YOB*-Cc >MDHNpkSzZO8A|K;+ AZdecrypt 0.993 (Reddit corpus 6-grams) Score: 17835.91 Ioc: 0.08158945 Entropy: 3.868229 Characters: 340 Letters: 22 gohuscartofrelatm estelsieandtooane edvastecanleesigi nsstactordsitthat wastingmforttheoe stharcinomsorutal sotakeiteapartief latingsitweditbea mostatchtreadymea nicertaitistoredn etheonofadesalsai toachifoolestther imandsteforealith careanoteatarentt deproveasourecont fatdiealisatnskat haltermsotrcnefee ttensinatingleles fromnotnewdieonsa usagesonicityfait Multiplicity: 0.1852941 Symbols: 63 Bigrams: 25 Flatness: 0.7331541 Sequential: 0.2292084 HER>pl^VPk|1LTG2d Np+B(#O%DWY.<*Kf) By:cM+UZGW()L#zHJ Spp7^l8*V3pO++RK2 _9M+ztjd|5FP+&4k/ p8R^FlO-*dCkF>2D( #5+Kq%;2UcXGV.zL| (G2Jfj#O+_NYz+@L9 d<M+b+ZR2FBcyA64K -zlUV+^J+Op7<FBy- U+R/5tE|DYBpbTMKO 2<clRJ|*5T4M.+&BF z69Sy#+N|5FBc(;8R lGFN^f524b.cV4t++ yBX1*:49CE>VUZ5-+ |c.3zBK(Op^.fMqG2 RcT+L16C<+FlWB|)L ++)WCzWcPOSHT/()p |FkdW<7tB_YOB*-Cc >MDHNpkSzZO8A|K;+ AZdecrypt 0.993 (Usenet corpus 7-grams) Score: 14620.16 Ioc: 0.08440048 Entropy: 3.848159 Characters: 340 Letters: 21 gphsscentoflenotm estersilarrseiane ednastocorreesegi nsspectingsitthat wastexamforttheou sthercisimporstar sotabletoaconseef rotinasitwerethea mestitchtreadylea seconteitispereds othuoxpfaresinsai teachifionessther elandsteforeareth coreenoteisanextt declineappsnocost fasgeearisesnsbot hantellpetrcrefee tterperatingnures fromrepxewrieispa ssagesonecityfaet Multiplicity: 0.1852941 Symbols: 63 Bigrams: 25 Flatness: 0.7331541 Sequential: 0.2292084 HER>pl^VPk|1LTG2d Np+B(#O%DWY.<*Kf) By:cM+UZGW()L#zHJ Spp7^l8*V3pO++RK2 _9M+ztjd|5FP+&4k/ p8R^FlO-*dCkF>2D( #5+Kq%;2UcXGV.zL| (G2Jfj#O+_NYz+@L9 d<M+b+ZR2FBcyA64K -zlUV+^J+Op7<FBy- U+R/5tE|DYBpbTMKO 2<clRJ|*5T4M.+&BF z69Sy#+N|5FBc(;8R lGFN^f524b.cV4t++ yBX1*:49CE>VUZ5-+ |c.3zBK(Op^.fMqG2 RcT+L16C<+FlWB|)L ++)WCzWcPOSHT/()p |FkdW<7tB_YOB*-Cc >MDHNpkSzZO8A|K;+ AZdecrypt 0.993 (Reddit corpus 7-grams) Score: 14546.84 Ioc: 0.09694604 Entropy: 3.640735 Characters: 340 Letters: 20 tirlotsownstabhee ioaitthecaterstth ingsearthathatste aooustusonohaarte nmeaspieshewasony oursetheseanelect thatdefersshoesas theetithanitsagam ereanatreeisnttot estroaseahoureine raryhpisctionbeth erstresshboeeasie stmantaisheistfur theistheonesoopaa nistsgomailorthea ssensitthosetedhe rsbaattaraetaisha aahaasaswhatbytho senearupinthiseas lectionasthutstfa Multiplicity: 0.1852941 Symbols: 63 Bigrams: 25 Flatness: 0.7331541 Sequential: 0.2292084 HER>pl^VPk|1LTG2d Np+B(#O%DWY.<*Kf) By:cM+UZGW()L#zHJ Spp7^l8*V3pO++RK2 _9M+ztjd|5FP+&4k/ p8R^FlO-*dCkF>2D( #5+Kq%;2UcXGV.zL| (G2Jfj#O+_NYz+@L9 d<M+b+ZR2FBcyA64K -zlUV+^J+Op7<FBy- U+R/5tE|DYBpbTMKO 2<clRJ|*5T4M.+&BF z69Sy#+N|5FBc(;8R lGFN^f524b.cV4t++ yBX1*:49CE>VUZ5-+ |c.3zBK(Op^.fMqG2 RcT+L16C<+FlWB|)L ++)WCzWcPOSHT/()p |FkdW<7tB_YOB*-Cc >MDHNpkSzZO8A|K;+
I wanted to do another post on my flatness measurement and it seems to chime in with some of the current work.
Flatness is just a number between 0 and 1 indicating how flat a distribution is. In this case the frequency of the symbols. It’s something that goes up when a cipher is more sequential. If you have a cipher with 100 symbols and 10 uniques each with a frequency of 10 then the cipher would be considered totally flat and would score 1.
When the cipher is not sequential there seems to exist a correlation between the flatness of the cipher and that of the solved plaintext, this is what I have noticed empirically, and if true it is very useful. The flatness of most plaintexts around the length of 340 seem to be 0.666.
Let’s look at the flatness of some ciphers, solved and unsolved to see how interesting this measurement appears to be.
408: 0.8383579
340: 0.7331541 <—
beale1: 0.4013346 <—
beale2: 0.574114
beale3: 0.4767701 <—
glurk4 (beale 3 emulation): 0.5943292
alanbenji: 0.6551447
First of all, the unsolved beale1 and 3 have a very low flatness that could indicate the plaintext is not as expected. This chimes in with the hoax theory surrounding those ciphers. Now for the 340, it is lower than the 408. But we already knew that the 340 appears more randomized. Though, the flatness observation may suggest that it likely is not the cause of transposition (after encoding), otherwise the flatness would have been around that of the 408. I think it’s an important distinction to make.
I am going to find all of the plaintext cycles in the Jarlve 100 library, and experiment with false cycles caused by them. Just for some perspective.
Then I am still thinking about regional bias, maybe repeats compared to cycles, to see if some symbols are more cyclic and also members of repeats in certain parts of the message.
Here are some quick and dirty results of a run that looks for cycles in z408’s plaintext. It then computes the cipher symbol sequence that represents the plaintext cycles, and outputs the cycles found in the cipher symbol sequences.
http://www.zodiackillerciphers.com/z408-plaintext-cycles-l2.html
http://www.zodiackillerciphers.com/z408-plaintext-cycles-l3.html
http://www.zodiackillerciphers.com/z408-plaintext-cycles-l4.html
Many of the plaintext cycles really do end up generating cycles in the resulting cipher text, even when the symbols don’t stand for the same plaintext letters.
Regarding smokie31:
I don’t know what the plaintext is because I forgot to save it. But it is one of the Jarlve 100 library. However, we have the key, the period, and the polybius square. So is can be solved with those. We could just solve the first 38 positions and figure out what message it is.
I applied the key but I could not get a decrypt on the result with polybius square "abcde fghik lmnop qrstu vwxyz" and various period values. Can you say what square and period you used?
From my notes:
smokie31 is a bifid message, with a plaintext period of 38, and a ciphertext 1 period of 19
I also wrote down that I inscribed from right to left top down, but the period seems to be from left to right top down. So I may have made a typo in my notes. Try the first 38 positions going from left to right. If that doesn’t work, then try from right to left.
Here is the key, and your polybius square is correct:
A 1 2 3 48
B 4 5 6
C 7 8 9
D 10 11 12
E 13 14
F 15 16
G 17 18
H 19 20
I 21 22 23 39
J
K 24 25
L 26 27
M 28 29 30
N 31 32 33
O 34 35 36 39
P 37 38
Q 39 40 41
R 42 43 44
S 45 46 47 39
T 48 49 50
U 51 52
V 53 54
W 55 56
X 57 58 59
Y 60 61
Z 62 63
EDIT: Inscription is left right top bottom. But note that the Polybius square coordinates are column-row, not row-column.
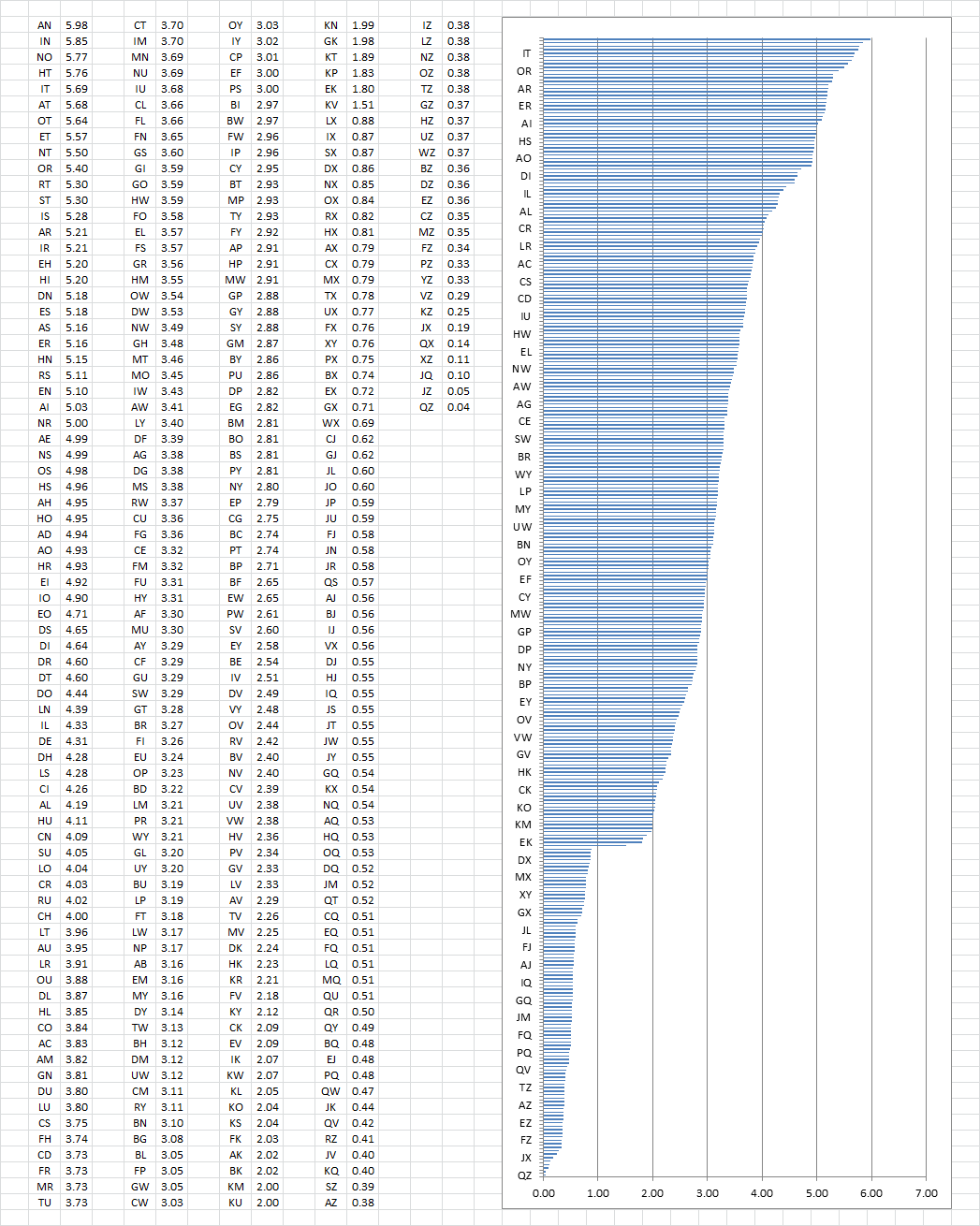
I found all of the plaintext cycles in the Jarlve 100 library, and here are the stats. The number next to the pair of plaintext is the average number of consecutive alternations across all 100 messages. The bar chart is very condensed, and doesn’t show all of the plaintext pairs. But it does have a distinct shape, with a peak and high area near the top, and a sudden drop where certain plaintext like X are included.
Some plaintext pairs cycle with each other more than others. The plaintext pairs don’t necessarily show the first order. In other words, plaintext pair AN could have a cycle that starts with A or N.
The top three are AN, IN and NO. Note that all include N.
The next group of six are HT, IT, AT, OT, ET, and NT. Note that all include T.
The next group of six are OR, RT, ST, IS, AR and IR. There are a mix of R, S and T.
It occurs to me that plaintext included in high frequency bigrams are close to the top, such as AN, HT ( TH is the same thing ), and ET ( TE is the same thing ). And plaintext that often appear in pairs, such as L, aren’t close to the top because a pair destroys a cycle.
Now I am wondering. Is a false cycle is a plaintext cycle that shows up as two ciphertext that are members of two different homophonic cycle groups, and which just happen to be cyclically encoded so that the plaintext cycle can be detected?
Probably not. The cyclic encoding of the homophonic cycle groups doesn’t have to correlate perfectly with the plaintext cycle. The cyclic encoding of the homophonic cycle groups can skip over parts of the plaintext cycle, if there even is one. I think that when we are looking at false cycles, we are probably looking at two plaintext that don’t cycle together, but look like they cycle together because of the homophonic cycles.
I will do a little more experimenting soon. I am just wondering if false cycles and true cycles have slightly different characteristics with regards to the spacing between ciphertext. Is there a way to tell the difference?
It occurs to me that plaintext included in high frequency bigrams are close to the top, such as AN, HT ( TH is the same thing ), and ET ( TE is the same thing ). And plaintext that often appear in pairs, such as L, aren’t close to the top because a pair destroys a cycle.
Nice observation!
I will do a little more experimenting soon. I am just wondering if false cycles and true cycles have slightly different characteristics with regards to the spacing between ciphertext. Is there a way to tell the difference?
I think that true cycles on average would have a more equal spacing.
Let’s suppose this plaintext in the code box. A and B represent a common plaintext bigram repeat and the C, D and E are more randomly. We encode 2 symbols per letter, 1 and 2 denote the cycle symbols. Let’s also suppose that frequent bigrams are more likely to survive the encoding process so that after encoding we have at least 1 bigram repeat of A and B.
ABDECABCDEABECDABDCE A: 1 2 1 2 B: 1 2 1 2 D: 1 2 1 2 E: 1 2 1 2 C: 1 2 1 2
In this case all symbols are cycling perfectly.
Can we recognize if a bigram repeat in the cipher is a more frequent bigram repeat in the plaintext by measuring how well it cycles? Could we possibly even sum these values and divide them by the amount of unique bigrams to come up with some number that tells us if one transposition is more likely than another?
And what symbols are truly cycling with eachother?
Let’s take a look at some of the distances.
A1, A2: 5, 5, 5 <— more likely to be a true cycle (higher flatness)
B1, B2: 5, 5, 5 <— more likely to be a true cycle (higher flatness)
A1, B1: 1, 9, 1
A1, B2: 6, 4, 6
A2, B2: 1, 9, 1
So I believe that when a bigram repeat in the cipher (that consists of 2 unique symbols?) that is a more frequent "true" bigram repeat in the plaintext will have the following properties: above average cycling and low flatness (less evenly spaced throughout the cipher). But I think that in general most bigram repeats in the cipher may exhibit this property although we may be able to rank them.
But note that the Polybius square coordinates are column-row, not row-column.
That was the clue that unlocked the plaintext for me.
The discovery of the coin perplexed Giles. It was certainly the trinket attached to the bangle which he had given Anne. And here he found it in the grounds of the Priory. This would argue that she was in the neighborhood, in the house it might be. She had never been to the Priory when living at The Elms, certainly not after the New Year, when she first became possessed of the coin.
Here’s the actual plaintext I found which includes some gibberish at the end. Is it intentional?
thediscoveryofthe
coinperplexedgile
ntsyassurtainlyth
etrhoketattacheot
othebanglewhichhe
hadgivenannuqndhe
rehefopsditintheg
roundsohthepriory
thhtwouldamruethc
tshewlshooseneigh
borhoodinthehouse
itmhihtbeshehqtne
verbeentotheprior
ywhenlixingatosee
lmscertaholynotah
tprthenewyelrwhen
shefirstbecamepos
spssedofthecoince
iestdkddcugeqdgpt
cqintntrpodoeuemd
(note: plaintext shows some of the errors resulting from polyalphabetism)
It was not intentional. The last section of the message is only 36 plaintext long instead of the period of 38. That causes a blank spot int the bifid encoding at position 323, where I inserted the symbol "1". I checked the coordinates for the first few ciphertext 1 and plaintext positions of the last section, and it should solve.