Thanks allot for these ciphers doranchak. I’m comparing them versus smokie’s transposition ciphers 9 through 15, smokie18e and the 340.
I’ve been trying to come up with a better way to define if a cipher is a thorough transposition or not. Here is, perhaps, some fruit of that labor. Though it may be possible that something other than transposition may be acting upon the measurement, so that is an assumption. I don’t want to share the system until I’m done with it. All the current numbers are subject to change.
A lower score is more indicative of transposition. None of the dpe# and smokie18e ciphers drop as low as the 340’s score of 9. Though, dpe3 and dpe7 have a score of about 25, similar to the smokie13, which is a transposition cipher. The 340 does not have a negative score (or very close to 0), so it is not over convincingly indicative of transposition, but it is not weak either.
To be clear. We don’t really know what the 340 is (we think we do, but we don’t). The 408, the dpe# series and the smokie18e are normal ciphers (doranchak’s and smokie’s period emulation). The smokie 9 through 15 are transposition ciphers with added difficulties.
340: 9 408: 125.34 dpe1: 56.07 dpe2: 54.96 dpe3: 25.61 dpe4: 49.96 dpe5: 38.84 dpe6: 47.46 dpe7: 25.53 smokie9: 9.03 smokie10: -16.88 smokie11: -33.53 smokie12: -34.65 smokie13: 25.11 smokie14: -21.46 smokie15: -33.30 smokie18e: 42.96
I modified my cipher generator to create ciphers that match these qualities of the original Z340:
- Same 1-gram distribution
- Same 2-gram distribution at period 1
- Same 2-gram distribution at period 19
- Presence of a pair of symmetrical pivots
- Presence of encoding errors
- Presence of filler section
- Similar appearances of "psuedo-words" in the raw ciphertext
- Spelling errors and missing words in the plaintext
[/list:u:14l1237e]
I did not optimize for things such as cycles and higher-order ngrams/fragments.
Here are 110 total ciphers generated by my hillclimber so far: http://zodiackillerciphers.com/generato … ent-54.txt
Back to the subject of whether he may have changed the key at intervals throughout the message when encoding.
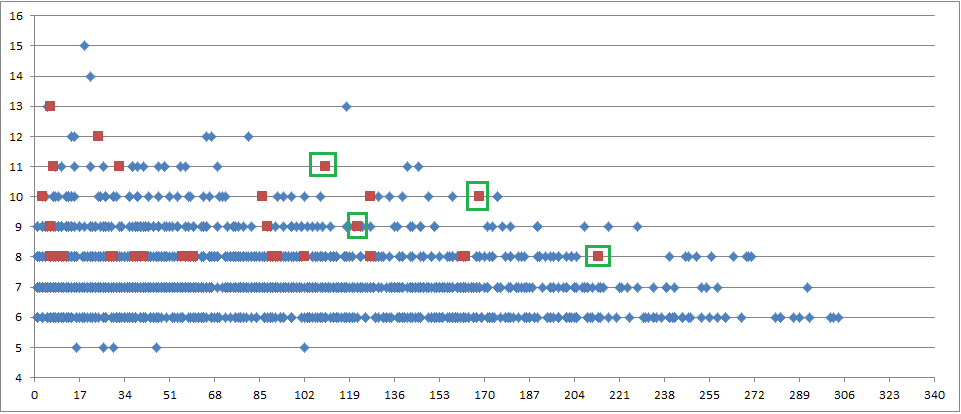
I shuffled the 340 fifty times, and for each shuffle I tabulated the top 33 scoring L=2 cycles ( the top 33 scoring 340 L=2 cycles have a minimum of 8 consecutive alternations ). Below is the scatter graph. The x axis is the position in the message, and the y axis is the number of consecutive alternations. There are 1,650 blue dots for the shuffle cycles, and 33 red dots for the 340 cycles.
I am just interested so far in the rightmost red dots, and comparing them to the blue dots for each number of consecutive alternations. From the 50 shuffles:
There were 17 occurrences of 11 alternations. Two started in positions to the right of the rightmost red dot ( 340 top 17% ).
There were 49 occurrences of 10 alternations. One started in a position to the right of the rightmost red dot ( 340 top 4%).
There were 130 occurrences of 9 alternations. Seventeen started in a position to the right of the rightmost red dot ( 340 top 14 %).
There were 368 occurrences of 8 alternations. Nine started in a position to the right of the rightmost red dot ( 340 top 3% ).
I don’t have any strong interpretation. But the stats are curious and by far the majority of shuffle results have L=2 cycles starting closer to the beginning of the message than these rightmost red dots. I wonder about how many shuffles it would take to exceed 340 stats for just both the 8 and 9 alternation categories. I may have to alter my testing a little bit to include lower numbers of consecutive alternations for the 340.
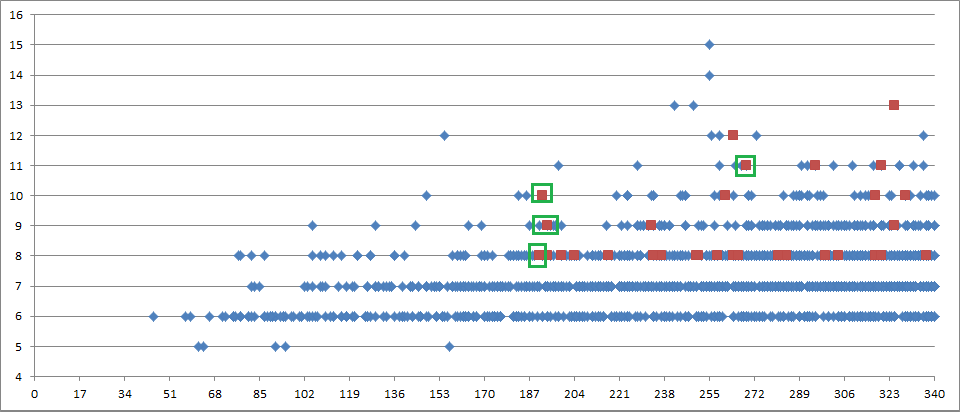
Here are the stats for end positions:
There were 17 occurrences of 11 alternations. Five started in a position to the left of the leftmost red dot ( 340 top 35% ).
There were 49 occurrences of 10 alternations. Three started in a position to the left of the leftmost red dot ( 340 top 8% ).
There were 130 occurrences of 9 alternations. Seven started in a position to the left of the leftmost red dot ( 340 top 6% ).
There were 368 occurrences of 8 alternations. Thirty two started in a position to the left of the leftmost red dot ( 340 top 9% ).
Thanks doranchak, when you’ve added all other stats (cycles and such) I’d like to do another comparison of some sorts.
Smokie, what do you think about the cycles?
Smokie, what do you think about the cycles?
I don’t know, but I am going to keep finding ways to look at them. I am going to look at cycles with fewer consecutive alternations, 7 and maybe 6. I find it interesting that some of the cycles with high counts of consecutive alternations start closer to the end of the message, but shuffling the message results in most of the comparable cycles starting closer to the beginning of the message. The 340 cycles that I found may not be true, and could be caused by overlapping true cycles.
Reading the older cryptography books has really helped me. I like the charts and tables and how cryptography allows for simple but creative ways to find solutions. It is amazing how people have solved very complicated messages with only paper and pencil. Seeing how others have solved other types of messages gives me ideas, and I am learning. Generally, however, I don’t find many of the books or websites to be well written.
I want to look specifically for situations where A cycles with B, but then the cycle stops and A starts cycling with C. If the transition area is closer to the beginning of the message, then generally AB should have fewer consecutive alternations and AC should have more. But if the transition area is closer to the end of the message, then generally AB should have more consecutive alternations and AC should have fewer. So I am thinking about making a simple table, with rows for symbols and 340 columns for position. Or vice versa. And charting where symbols start and stop cycling with each other. Just looking at cycles with high numbers of consecutive alternations.
Then shuffle the message to see if the tables are very much different. If it happens a lot more with the 340 than with shuffled. If so, then start making test messages with just random symbol selection to disrupt the cycles. See if the tables are different. If so, then start making test messages with cycled cycles.
Classical cryptography books show pictures of different kinds of rotating disks, and machines with rotating gears. He liked to cycle stuff, and was very creative. And he liked to copy stuff. I just wonder if he may have made some type of crude rotation device. Like maybe where he would encode for a while, then turn or rotate, then encode some more, turn or rotate, etc. Or maybe the device is two dimensional. Just something that you could do with paper and pencil very easily. I wonder if that is why the L=3 cycles are disrupted.
Smokie, what do you think about the cycles?
I don’t know, but I am going to keep finding ways to look at them. I am going to look at cycles with fewer consecutive alternations, 7 and maybe 6. I find it interesting that some of the cycles with high counts of consecutive alternations start closer to the end of the message, but shuffling the message results in most of the comparable cycles starting closer to the beginning of the message. The 340 cycles that I found may not be true, and could be caused by overlapping true cycles.
A few days ago I made a cipher with supercycles (cycles that cycle). I went all they way, with as many supercycles as possible. It or I failed so hard that at the end the cipher was cycling negatively versus randomizations. It’s not an easy thing to go about and I would only recommend it for the higher count letters. I’ll see if I can make another try.
Reading the older cryptography books has really helped me. I like the charts and tables and how cryptography allows for simple but creative ways to find solutions. It is amazing how people have solved very complicated messages with only paper and pencil. Seeing how others have solved other types of messages gives me ideas, and I am learning. Generally, however, I don’t find many of the books or websites to be well written.
Pen and paper is much more tangible.
I want to look specifically for situations where A cycles with B, but then the cycle stops and A starts cycling with C. If the transition area is closer to the beginning of the message, then generally AB should have fewer consecutive alternations and AC should have more. But if the transition area is closer to the end of the message, then generally AB should have more consecutive alternations and AC should have fewer. So I am thinking about making a simple table, with rows for symbols and 340 columns for position. Or vice versa. And charting where symbols start and stop cycling with each other. Just looking at cycles with high numbers of consecutive alternations.
It is also possible that ABC is a true cycle that works that way. Though, it makes less sense. Also because the 340’s key is less flat than the 408, possibly something acted upon it that affected the frequencies of most symbols.
Classical cryptography books show pictures of different kinds of rotating disks, and machines with rotating gears. He liked to cycle stuff, and was very creative. And he liked to copy stuff. I just wonder if he may have made some type of crude rotation device. Like maybe where he would encode for a while, then turn or rotate, then encode some more, turn or rotate, etc. Or maybe the device is two dimensional. Just something that you could do with paper and pencil very easily. I wonder if that is why the L=3 cycles are disrupted.
I agree, he liked to copy stuff, that is something that people on the board are finding out. He sourced allot of material. I am very skeptic about a rotating device for encoding. There is a strong directional bias to the encoding, it clearly goes from left-to-right, top-to-bottom.
Smokie, a while back ago I made a mathematical cipher that somewhat cycles of its own. I think the algorithm is not a good hypothesis but perhaps it might be interesting to look at its cycles. The cipher is very polyalphabetic and it’s interesting to see that its bigrams are unaffected (did not shift because of polyalphabetism). Strong returns from period 1, 2 and 3. The plaintext is the 408.
http://www.zodiackillersite.com/viewtop … mic#p29105
Original format: ----------------------- 8DMX]h1=IR`g7<K[g []bef;NS9L_n;PS JPe3<PYl9HZ_e:Hd Tbm6BNWelCLXcd16 n<PX]c2DV[nBDILMb di67ENa5=BO^1EIJX NSe4I]k4ABN]cd0< ?NYbn:MinBJSah/8 =BUbg;CHUd7K_g9BN IR`glDTYk0>AFOcl? 3IN^c7KPb6>?MTYm 09GNg6K]/>AL_n4:Q I]efm6HTh057<Oc34 5IX^g;DWk34H_gl:C 6?DMdm9EGL^ce4FT] Zjk=>BKNSTbfg3?S[ OX`a7<GPhm1HQ]ik _b1>CPi<HI_d7@W`l g5DX_h>Ck@Mf45BG 8=@AVinGVkBKWc7Ib Numbered by appearance: ----------------------- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 12 16 5 17 18 19 20 21 22 23 24 25 26 27 28 20 29 22 30 29 18 31 14 29 32 33 25 34 35 27 18 36 34 23 37 38 17 39 40 41 21 42 18 33 43 26 4 23 44 37 7 40 28 14 29 4 5 44 45 2 46 16 28 41 2 9 26 3 17 37 47 40 13 48 21 49 50 8 41 51 52 7 48 9 30 4 21 22 18 53 9 23 5 54 53 55 41 21 5 44 37 24 14 56 21 32 17 28 36 3 23 47 28 41 30 22 49 6 57 1 8 41 58 17 12 20 43 34 58 37 13 15 27 12 25 41 21 9 10 11 12 33 2 38 32 54 24 59 55 60 51 44 33 56 31 9 21 23 52 44 13 15 29 17 40 59 56 3 38 32 39 24 25 61 21 12 40 15 5 57 59 55 26 27 28 53 36 62 9 5 18 19 39 40 34 38 6 24 50 13 14 51 44 31 53 50 9 4 52 12 20 2 42 54 31 53 34 27 12 33 36 43 40 56 2 3 37 39 25 48 61 26 52 44 18 53 60 38 5 35 63 54 8 59 41 15 21 22 38 17 19 12 31 56 22 16 51 4 11 49 13 14 61 29 23 6 39 7 34 62 5 47 54 27 17 7 59 43 29 47 14 34 9 27 37 13 64 42 11 33 12 50 2 4 27 6 59 43 23 54 64 3 19 53 50 41 61 1 8 64 55 46 47 28 61 46 54 41 15 42 44 13 9 17
The last few days I have been looking mainly at transposition. The 340 has a stronger bigram response when it is mirrored or flipped, horizontally and period 19 vs 15 etc. If you then cast the mirrored / flipped 340 in the dimensions 14 by 25 / 16 by 22, some of the diagonal untransposition score very high. In particularly the 16 by 22 (doranchak’s find I think) was interesting to me and I came up with a hypothesis.
Assuming transposition,
The 340’s plaintext was diagonally transposed into a 16 by 22 rectangle starting in the bottom-right corner. The next image shows then the problem which is created (p1 plaintext).

The top-left corner is missing and after compressing the cipher it becomes rather unsolveable until you either correctly insert the nulls at each row or chop off the entire section (its head). I tried both options for the record and did not get a solve. This creates period 15 repeats, that’s good.
The next step in the hypothesis is to take off the rows from bottom-to-top into a 17 by 20 rectangle and we should have period 19 repeats in the left-to-right, top-to-bottom direction, right? Wrong, because we are taking of the rows bottom-to-top in 16 by 22 (or right-to-left with the 14 by 25) the period changes to 17, doh!
So for the hypothesis to work, it means that Zodiac transposed the 16 by 22 diagonal transposition left-to-right, top-to-bottom into a 17 by 20 rectangle and then either mirrored or flipped it. I find that unlikely. Also, while these untranspositions are very strong, (mainly the 16 by 22) period 2 bigrams are missing.
What I also looked for is that perhaps 2 transposition rectangles were used but could not really find it. Though there is a small relative peak at 13 by 22, 3 by 22 which seems unlikely. I still think the 14 by 25 and 16 by 22 diagonal transpositions may be a step in the right direction or somehow share properties with the actual scheme and currently have some AZdecrypt tests running.
There a few things bothering me at the moment.
– Period 2 bigrams are missing from these manipulations. Where are they?
– Why is the mirrored and flipped 340 so much stronger (bias), also horizontally?
– The mirrored/flipped bias could suggest another step, like taking off a transcription in another direction, though then the rectangle must have been 17 by 20 to begin with. Would this not be more suggestive that the transposition happened in a 17 by 20 rectangle?
– Some of the (un)transpositions we have come up with (simple things that are not molding) are very strong, almost approaching the stats of the 408 but don’t solve.
340f_16by22_dia_utp_c4b: Original format: ----------------------- L*1z<|K#.k/RLYP_k +)WV8(4+(D^+pD&OW %lJ5|2+pGOpb2#L>P 3Z#>++G9zFFVU(REV M(L.k5*+BEd*tU<K@ VC|8M+H2||5ld4+Gd dlcp)GbNJ/z-6zX*j ^:NfT>4+RR-yAYc-t 7yJK.E2#l+OByNUOz pBHW^C5ycUKFc_2l+ p2/lp9fS<FM<B+;FM S-TFO4^92BT7FO%^9 ;*H+(:N6R&bp2#qRK BS<K*Fz8+pORjK|OO CB1G+;.B+ZfAYP6zX l+(MYJ+8_c13B+tc4 D^OBWL.y-4BT|Ztz+ c25VF5z7CT|GZc5S< WcLqU.kW)R)MVpd+p |fNk+)BHFc(D|CM+> Numbered by appearance: ----------------------- 1 2 3 4 5 6 7 8 9 10 11 12 1 13 14 15 10 16 17 18 19 20 21 22 16 21 23 24 16 25 23 26 27 18 28 29 30 31 6 32 16 25 33 27 25 34 32 8 1 35 14 36 37 8 35 16 16 33 38 4 39 39 19 40 21 12 41 19 42 21 1 9 10 31 2 16 43 41 44 2 45 40 5 7 46 19 47 6 20 42 16 48 32 6 6 31 29 44 22 16 33 44 44 29 49 25 17 33 34 50 30 11 4 51 52 4 53 2 54 24 55 50 56 57 35 22 16 12 12 51 58 59 13 49 51 45 60 58 30 7 9 41 32 8 29 16 27 43 58 50 40 27 4 25 43 48 18 24 47 31 58 49 40 7 39 49 15 32 29 16 25 32 11 29 25 38 56 61 5 39 42 5 43 16 62 39 42 61 51 57 39 27 22 24 38 32 43 57 60 39 27 28 24 38 62 2 48 16 21 55 50 52 12 26 34 25 32 8 63 12 7 43 61 5 7 2 39 4 20 16 25 27 12 54 7 6 27 27 47 43 3 33 16 62 9 43 16 37 56 59 13 14 52 4 53 29 16 21 42 13 30 16 20 15 49 3 36 43 16 45 49 22 23 24 27 43 18 1 9 58 51 22 43 57 6 37 45 4 16 49 32 31 19 39 31 4 60 47 57 6 33 37 49 31 61 5 18 49 1 63 40 9 10 18 17 12 17 42 19 25 44 16 25 6 56 50 10 16 17 43 48 39 49 21 23 6 47 42 16 35
Thanks doranchak, when you’ve added all other stats (cycles and such) I’d like to do another comparison of some sorts.
OK – For now, I added the L=2 "perfect cycle score" (defined here) as one of the objectives. Here are 56 generated ciphers that have unigram, bigram (period1+period19), and pcs (L=2) scores similar to the unmodified Z340:
http://zodiackillerciphers.com/generato … ent-55.txt
Thanks doranchak, when you’ve added all other stats (cycles and such) I’d like to do another comparison of some sorts.
OK – For now, I added the L=2 "perfect cycle score" (defined here) as one of the objectives. Here are 56 generated ciphers that have unigram, bigram (period1+period19), and pcs (L=2) scores similar to the unmodified Z340:
Thanks, are these the final renditions?
I’ve let AZdecrypt run on the 340 for over an hour with the possibility of either keeping the normal orientation, mirroring, flipping or reversing and diagonal transposition. Here’s the best result, it is interesting because it has a high score and a normal index of coincidence.
AZdecrypt 0.993 (Practical Cryptography 5-grams) Manipulation operation(s): Flip(17,20,1), Diagonal(16,22,1,1,2,1) Score: 20807.93 Ioc: 0.06637168 Entropy: 4.030919 Flatness: 0.7058824 Chi-square: 21.02345 Bigrams: 178 Letters: 20 poadderssensonded tortwascsingemasi thislydidthiswils oheldinutagainere useonlasanontarof thesthelongboyand eediocetonhsmithn icmultancedfroemb arrestinlaruesith asbontastheatfilt oflassiesaidrient heedaneofulaginat etsthatccoupiedfr omthethindaystsfr ryourfiddleoanddw hiteemranomingara wacrewsshayoopull spaulateytoldinfr ienetorerournwiso nastacinguidthama Multiplicity: 0.1852941 Characters: 340 Symbols: 63 Bigrams: 41 Flatness: 0.7833966 Sequential: 0.1492269 >+MC|D(cFHB)+kNf| p+dpVM)R)Wk.UqLcW <S5cZG|TC7z5FV52c +ztZ|TB4-y.LWBO^D 4ct+B31c_8+JYM(+l Xz6PYAfZ+B.;+G1BC OO|KjROp+8zF*K<SB KRq#2pb&R6N:(+H*; 9^%OF7TB29^4OFT-S MF;+B<MF<Sf9pl/2p +l2_cFKUcy5C^WHBp zOUNyBO+l#2E.KJy7 t-cYAy-RR+4>TfN:^ j*Xz6-z/JNbG)pcld dG+4dl5||2H+M8|CV @K<Ut*dEB+*5k.L(M VER(UVFFz9G++>#Z3 P>L#2bpOGp+2|5Jl% WO&Dp+^D(+4(8VW)+ k_PYLR/k.#K|<z1*L
Thanks, are these the final renditions?
My plan is to gradually add more objectives (prime phobia, for example). I’m not sure how important they are. And if I add too many objectives, the search tends to get slow or stuck. Also, since I’m still rather curious about columnar transposition, I might try to generate some ciphers that have transposition applied before encipherment. It may be more fruitful to work towards strongly excluding columnar transposition as a hypothesis. Then I can gradually create more test ciphers under more schemes. I think the focus should be on gathering stronger evidence for or against specific schemes.
Smokie and doranchak. I made a message with some difference in the encoding that also makes it unsolveable. I didn’t try to match 340 stats but I wonder how it compares.
p105_jarlve_e1.txt 8#C.3E+]J@9'R#OJT UdVLB1EH&cTEh44e! ,*a`iZ&:3V<AK`*)I :e<7/GIY8`CP_@QKg O^>TcER4'%ZR]=#' BahTEH^><XOdLY:=( `2(i9!)@/&OGFIQi3 ,^AX4P/_*Q^ce8BO> :CcEcRLT3RZY24,U +aV<XA#EV)E^`@=,Z KF]8G_PYP*:*/T12 V)QI/87XG=G'3&R> He%c[SLR/6dEg)A]J ,.=1.9a_H()ZB1V)C cL!62^)<@1iF#4#i, *3.)UY_!K/`QQ:'B >`IOLG%JO297&dE+I (Qg62]]U=TP^i6.X U8YAB.Y(6'6EH..SK FR#I!//3Zh+_+3QPe 1 2 3 4 5 6 7 8 9 10 11 12 13 2 14 9 15 16 17 18 19 20 21 6 22 23 24 15 6 25 26 26 27 28 29 30 31 32 33 34 23 35 5 18 36 37 38 32 30 39 40 35 27 36 41 42 43 40 44 1 32 3 45 46 10 47 38 48 14 49 50 15 24 6 13 26 12 51 34 52 13 8 53 2 12 20 31 25 15 6 22 49 50 36 54 14 17 19 44 35 53 55 32 56 55 33 11 28 39 10 42 23 14 43 57 40 47 33 5 29 49 37 54 26 45 42 46 30 47 49 24 27 1 20 14 50 35 3 24 52 6 24 13 19 15 5 13 34 44 56 26 29 16 7 31 18 36 54 37 2 6 18 39 6 49 32 10 53 29 34 38 57 8 1 43 46 45 44 45 30 35 30 42 15 52 21 56 18 39 47 40 42 1 41 52 54 43 53 43 12 5 23 13 50 22 27 51 24 58 59 19 13 42 60 17 6 48 39 37 8 9 29 4 53 21 4 11 31 46 22 55 39 34 20 21 18 39 3 24 19 28 60 56 49 39 36 10 21 33 57 2 26 2 33 29 30 5 4 39 16 44 46 28 38 42 32 47 47 35 52 12 20 50 32 40 14 19 43 51 9 14 56 11 41 23 17 6 7 40 55 47 48 60 56 8 8 16 53 15 45 49 33 60 4 52 54 16 1 44 37 20 4 44 55 60 12 60 6 22 4 4 59 38 57 13 2 40 28 42 42 5 34 25 7 46 7 5 47 45 27