I have a lot of things on my to do list, and grille cipher is definitely one of them. I woke up this morning with an idea:

Hill climb the perforation positions in a grille to maximize period 15 / 19 repeats and pivots. With grille, square grids of plaintext are anagrammed, and then drafted into the message grid. Relative perforation positions are not transferred directly into the message grid. But I still think that certain grille patterns could increase the probability of creating pivots. So the idea is to hill climb different grilles to maximize certain stats, and then use them to try to solve the 340.

OK – here is my post about how I’m exploring different encipherment schemes using generated test ciphers: viewtopic.php?f=81&t=3108

BartW I have never been able to emulate the same results from a scytale crypto tool as I have from manually constructing and deconstructing back to a 17x 20 format. When I get a chance I will dig out my original 19 scytale..

Also can some one run the below through a solver..it’s a row scytale .. Note the first column down.. May need to run it through from top to bottom as well. I’m on I pad for a few days..

ABCDEFGHIJKLMNHOL
PQDNBRSHTUVWMQSIX
AOYZaEbKcdBDeBfHB
PghDCBiGBjUEkLXlE
SmnKoUeIpqUSrHIIX
BsqoUfYktIjlSBQiu
SvVPwUxmWMEYLLNFV
BWOtyz0v12ZeKByoF
nJddeHk3YBBZD4Ukb
yjMyDr2LrOBVm1uwF
z0WwxFOcyePjGRKZO
BB5KWBZQk4BKQgQBL
vJ64FmlBaKfUHTqCy
ABGBia7HpzOjurnFj
JmljUXs5DvmP84Vhm
4iFXHopsjSERPDjUB
uKh9k3lqSr8DtbdSH
xLqdC!XDJ!DKN9ydF
FZ4RkL0MABXhNG2NO
HHL7xeknrjskjbSex

BartW I have never been able to emulate the same results from a scytale crypto tool as I have from manually constructing and deconstructing back to a 17x 20 format. When I get a chance I will dig out my original 19 scytale..

It would be interesting if you find it for comparison. A syctale is normally used rowed pt to sequential cipher text.

Also can some one run the below through a solver..it’s a row scytale .. Note the first column down.. May need to run it through from top to bottom as well. I’m on I pad for a few days..

AZdecrypt 0.992 (Practical Cryptography 5-grams) Normal, Index of coincidence
Score: 19668.38 Ioc: 0.07102203 Entropy: 3.905491 Chi-square: 63.98745 Characters: 340 Letters: 18

stnotmuchfilescal
lmostsschneremshe
sayertrinetostact
ledontoutintalent
sasionshuinsuchhe
ttionayanhinstmod
srelinaaretyllsme
trandburnbesitdom
sfeescarytteornar
diedoubluateandim
buriamandsliusiea
tthirtemartimemtl
rformantrianchind
stutorecubaidusmi
faninethoralpreda
romecoutistsloint
didearnisuponresc
alienceofcoisedem
mersaluestedsubsa
ccleasasuitairssa

Multiplicity: 0.1852941 Characters: 340 Symbols: 63

I am working on the grille cipher, wondering if I can make a grille that replicates 340 repeat stats. I am not confident that it will work, but I have to get this resolved. The period 15/29 or 19/39 repeats are the issue. Below is a preview of my grille making spreadsheet. It took just a couple of hours. I can make random grilles over and over again with a single click. I would like to maybe hill climb grilles to maximize period 15/19 repeats. If so, also create a lot of period 29/39 repeats.

I am working on the grille cipher

I have thought about the grille also but i can’t think of a proper way to implement it.
I am glad you are take it on. Perhaps we can collaborate in a new thread… to me grille is almost an otp.
By definition a grille can be any location read in any order.
the lack of rule/order make this a tricky problem to solve for.
I have considered a few ideas such as the box sections and others anomalies as location markers.
Even the ‘+’ potential could be a mask pattern…. arghhhh.

Regards
Bart

I am not too excited about the 340 being a grille underneath the homophonic ciphertext. It seems to me that it would be very difficult to make a grille that can create so many period 15/19 repeats. But, I imagine if a grille that could do that it would have some type of pattern. I would like to see what such a pattern may look like.

Note that there are more period 39 repeats than there are period 38 repeats, and the pivots are made up of period 39 repeats. Also, if you read the message from right to left, top row to bottom row, there are almost as many period 29 repeats ( not period 30 ) repeats, as there are period 15 repeats. A period 15 repeat is a mirrored period 19 repeat. You should take a look at that.

A grille anagrams square chunks of plaintext which is then transcribed into the message grid that may not be the same width of the grille. Therefore any box or pivot configuration would not appear so on the grid itself.

I chose an 8 x 8 grid because 64 * 5 = 320, and that gets us close to 340. If it looks promising I may have to look at a 6 x 6 grid because 6 x 6 x 9 = 324.

Maybe a grille wouldn’t be so difficult to solve? It would be anagrammed chunks of 64 plaintext. All five chunks of message would have to be rearranged the same way, so making correct changes to all may be recognizable.

But enough of that for now, I just want to know if it is possible to make a message with so many period 15/19 repeats. I am guessing that it is not.

I am working on the grille cipher[/quote]
[quote="BartW":2q4whdrs]Even the ‘+’ potential could be a mask pattern…. arghhhh.

A while ago I tried to put the z340 on top of the z408 and write down all letters from z408 with a matching "+" symbol at the z340 (shifting it down four times since z408 has 4 rows more that z340).
I’ve tried the same with rotated z340.

Obviously I found nothing.

I’ve also had the idea that a "turning grille" could be the solution to z340. Since a turning grille must be a square and the number of the fields has to be a multiple of four some rows/columns from z340 could be filler (e.g. the first three rows and the last column) to produce a 16×16 grid. I discarded the idea because there are too many possible solutions.
There is an interesting article about turning grilles on wikipedia. Unfortunately the mathematic part is only available in german. In this article is described how to calculate the number of possible turning grille ciphers:

https://de.wikipedia.org/wiki/Fleissnersche_Schablone

Maybe a turning grille with 2 rotations was used? This would be much easier because it would fit to non-squared ciphers too.

Since a turning grille must be a square and the number of the fields has to be a multiple of four some rows/columns from z340 could be filler (e.g. the first three rows and the last column) to produce a 16×16 grid. . . . Maybe a turning grille with 2 rotations was used? This would be much easier because it would fit to non-squared ciphers too.

Alexander Hamilton, one of the American founding fathers used a turning grille cipher. And the article on wiki is very interesting. They were popular in the 18th century, the German army used them in WWI, and Jules Verne wrote about them in one of his novels. Turning grilles are also discussed in early 20th century cryptography books.

Note that the size and shape of the message do not have to be increments of the grille size. The grille anagrams square chunks of message, which can then be transcribed into the final message which can any number of rows and columns. I believe that is the way that the grille was historically used.

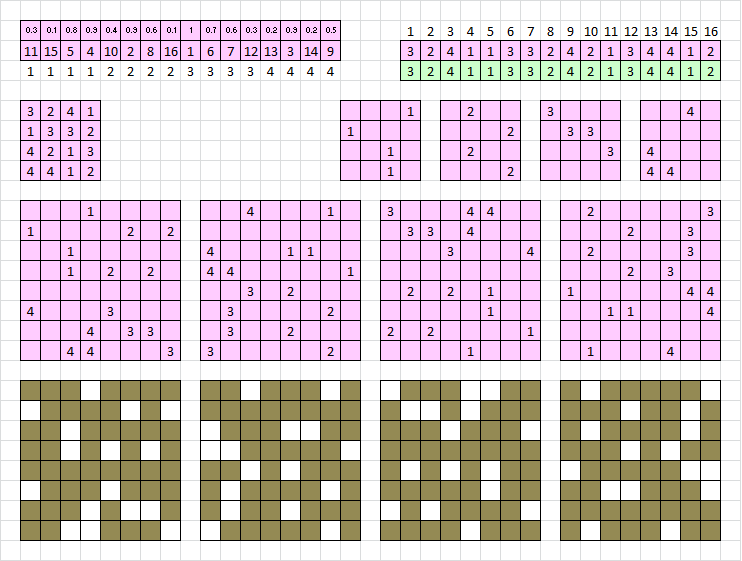
My spreadsheet is coming along. Lower left is the final product in terms of original plaintext position, and I have a little distribution of period 1 position spacings post anagram. With this example, there are a lot of period 1 position spacings anagrammed into period 3 position spacings. You can confirm that by looking at the perforation configurations. The different colored cells just help me to keep my formulas mentally organized.

He didn’t use an 8 x 8 rotating grille. I tried to make a grille that could result in a lot of period 15 repeats, with simple hill climbing and trial and error, but it didn’t work. I also generated a lot of random grilles.

Basically with a rotating grille, there are going to be a lot of period 1 to x repeats, where x is the width of the grille. There is sometimes a small bump at between x + 1 and 2x. That is because with a 8 x 8 grille, which has 64 squares, you have to perforate 16 of those squares. Four in the NW corner, four in the NE corner, four in the SE corner, and four in the SW corner. Each 4 x 4 corner is a clockwise rotation of the corner behind it, and the none of the perforations can land on the same position more than once.

With those rules, I was not able to make an arrangement of perforations that resulted in more than 20 period 15 repeats throughout the entire 340. That is because I could not avoid putting more than one perforation in a row enough times. Perforations can increase the number of period 15 repeats, but then I had to add more perforations, and that destroys period 15 repeats.

Below is an example of a random grille. This grille would result in a lot of period 1 and 3 repeats, and there is a little bump at period 10, 12 and 13. I tried to make configurations to shift the values to the right on the column chart, where x is the period and y is the count of possible repeats for the entire 340.

Based on this experiment, I doubt that a square rotating grille was used, at least if the anagrammed message chunks were subsequently transcribed into the message 17 x 20 grid. Maybe another possibility is what Largo said, a square or rectangle grille rotated 180 degrees. It seems doubtful, though.

I want to look at regional differences with the repeat stats. The row / column shuffle tests worked very well at identifying individual rows or columns not transposed as compared to the rest of a route cipher message. I made a new spreadsheet so that I can shuffle any region of any shape, or multiple regions at the same time. I am going to experiment with that.

I have a new shuffle spreadsheet, where I can select or exclude any of the positions for regional shuffle tests. And I can make 100 shuffled messages with a single click. I am going to be making some test messages that are combinations of different transposition schemes in different regions and then shuffle those different regions to see what happens to various stats. Below the yellow shaded cells are selected to demonstrate the variety of different position schemes that I can select. Remember when the 340 is drafted into 19 columns and two of the columns don’t have any repeats in them? That is on my to-do list, as well as other regions of the 340.

Still working on the 340 to the best of my capabilities, and not ready to give up.

Doranchak pointed out that columns 3 and 4, when the message is drafted into 19 columns, do not have any period 19 repeats, so I looked at that. Top is period 19, middle is period 38, and bottom is period 57. There are repeats at period 38 and 57.

I checked all of doranchak’s 119 scytale messages, and thanks for doing that. Thirty four of the messages had one of 19 columns without repeats. But only message number 80, of the 119 messages, had two or more columns without repeats. That is less than 1%, and maybe that is important. Here is message 80.

I was wondering if maybe he drafted the message vertical, and then added nulls, which make up columns 3 and 4 to hide the direction of the plaintext. So I drafted the 408 plaintext vertical, added nulls in the same locations, and untransposed at period 19. It would have solved.

EDIT: I checked the 110 homophonic messages. There were 21 with one column without the repeats, and only four with two columns without repeats ( messages 25, 45, 96 and 108 ).

Some of the pivot symbols are in columns 3 and 4. See the red boxed symbols on the right. 34.7% of the positions are highlighted, but only 1 of 9 pivot symbols ( not counting the axis symbols ) are highlighted.

I have a new shuffle spreadsheet, where I can select or exclude any of the positions for regional shuffle tests.

Looks like you are doing some awesome work Smokie.
I have been considering the grille but i can’t not see any valid or worthwhile input that i can offer.
The pure definition of the Grille is such that I can not see any way of efficiently attacking it.
I have been looking through the ACA Cipher lists looking for potential ciphers that are not main stream yet show a similar trait – BTW no luck so far.

Regards
Bart