I am glad everyone is still trying out new ideas. Keep it up!
Any break-throughs, or progress Guys?
No major breakthroughs lately, but I am still working on it. I do think that a lot of progress has been made in the last year. Statistical evidence shows that the 340 is not just a random assortment of symbols, and we have eliminated a lot of possible ciphers. The message is very unique, and I hope that someday it may be solved. Thanks for the website. I appreciate it very much.
I agree with smokie’s assessment. Lots of progress has been made. New leads have been pursued in some recently discovered statistical clues within Z340. It has led to a flurry of new ideas about how to find schemes that could leave behind similar clues.
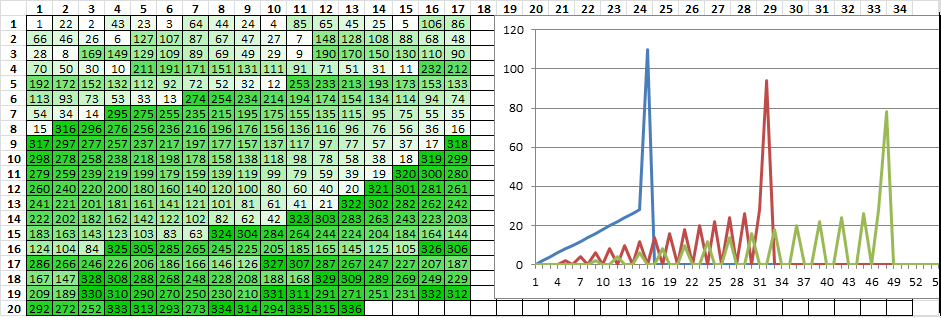
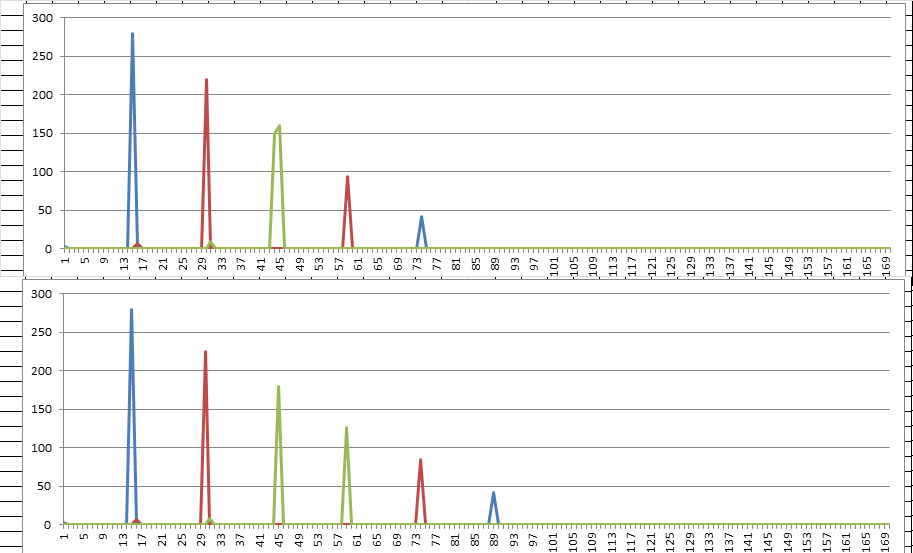
OK so for the mirrored 340, we have a peak of 41 repeats at period 15, and a second peak of 34 repeats at period 29. I also see that there is another peak of 33 repeats at period 110. Do you see the same count for period 110?
110 does not seem to be near a multiple of 15 or 29, so is it just a phantom? Could the period 29 peak be a phantom and not a true reflection of the period 15 peak + misalignment? Or perhaps the period 110 peak is also some evidence of this misalignment?
I am still working on the 340. I have a new spreadsheet suite where I can make transposition tracing maps for multiple rectangles, complete and incomplete, diagonal transcription, and multiple smaller inscription rectangles. I have been working on it since the summer and looking at thousands of different transposition patterns to find a scheme that could emulate what we have been observing ( repeats, pivots, coincidence count, etc ). And I am just starting on thinking of ways to detect more complicated transpositions other than just one big rectangle. I only work on it a few hours EDIT: several hours a week, but that is good because it gives me time to think. I will keep period 110 in mind and post in the future.
EDIT 2:
Remember the apparent regional biases? For example below are the original orientation period 39 repeats and pivots with the void area the upper left.
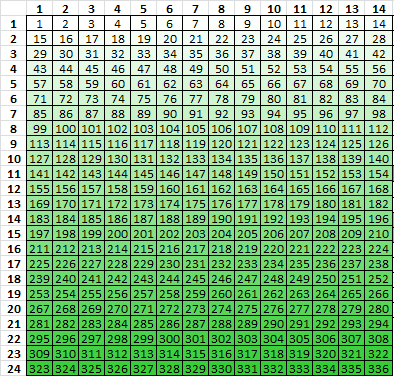
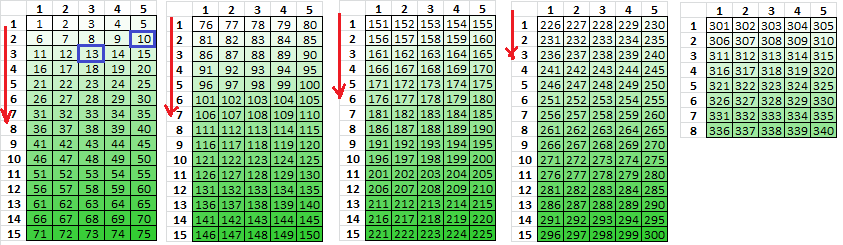
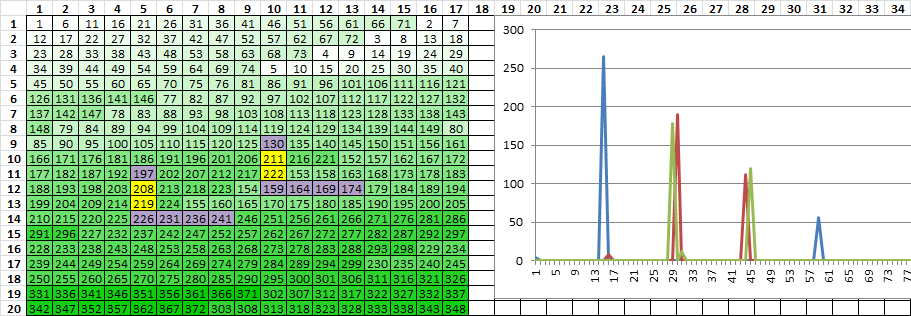
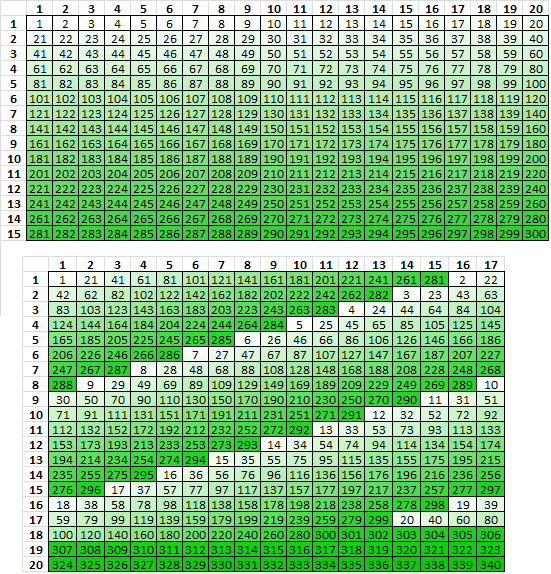
One way to make a transposition with regional biases is with multiple rectangles where intermediate rectangles are incomplete. For example below, the first rectangle is 14×24, with inscription left to right, the numbers are message plaintext positions with cell shading conditioned on value.
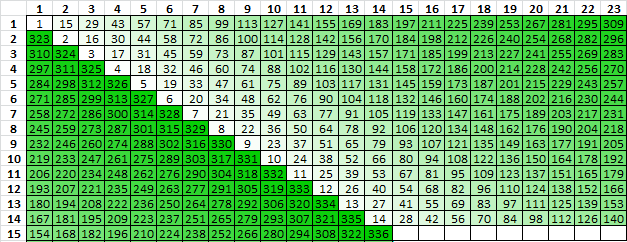
The second rectangle is 23 columns wide, the positions lifted from the first rectangle vertically top bottom left right, and transcribed horizontal left right top bottom. The bottom row is incomplete.
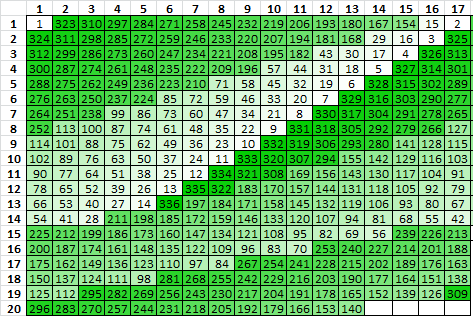
The third rectangle is 17 columns wide, positions lifted from the second rectangle vertically top bottom left right, and transcribed horizontal left right top bottom.
I will show some more interesting examples shortly.
Here are some cool transpositions with four rectangles, some complete and some incomplete.
The sheet also makes little graphs showing period spikes. Period 1 Blue, period 2 red, period 3 yellow.
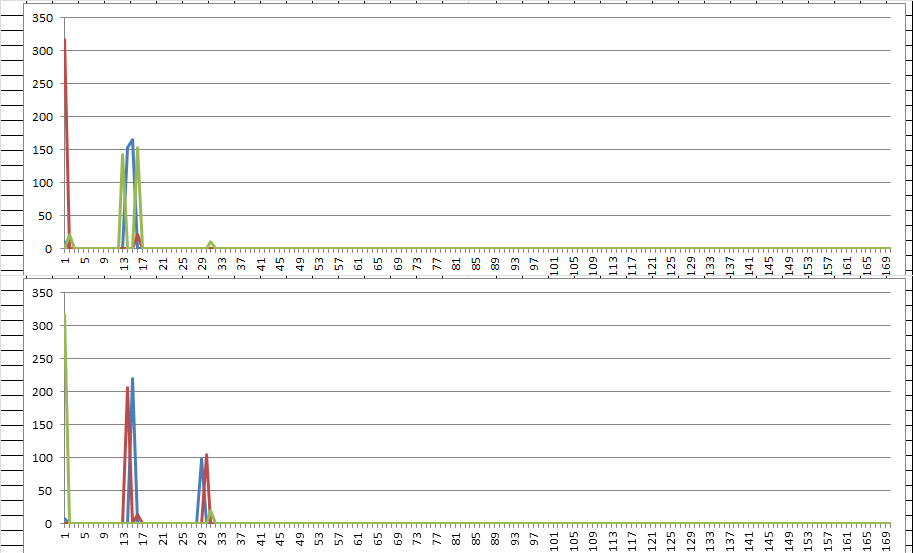
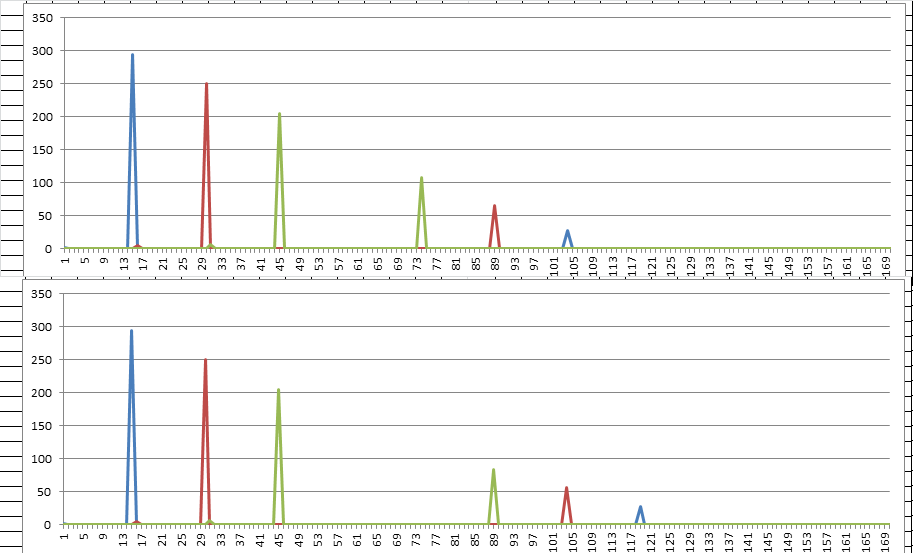
Here is one with a regional bias that has spikes shifted to much higher periods. Scroll to the right to see the spikes.
Maybe period 110 is created by multiple rectangles. But maybe it is just that the key diffuses period 110 less than the others.
Anyway, I can do complete or incomplete rectangles with vertical or diagonal transposition at each rectangle step. There are thousands of possibilities but I have not found one that looks exactly like the 340, with period 15 / 19 throughout, lower half period 29 / 39, and pivots. That is just one big rectangle after another. Not smaller, multiple rectangles transcribed into one big rectangle.
More posts coming.
Anything more than 4 rectangles with vertical transposition just turns out to be a mess.
Here is a cool one. Two rectangles only with diagonal transposition.
More later.
Hi smokie – thanks for your updates. I had been wondering if you were still working on this. Very interesting approach you are taking with rectangular transposition. If Z340 is encoded this way, I’m wondering how you’d be able to determine which scheme is in play. Maybe a specialized hillclimber can look for the untransposition that minimizes the regional biases (i.e., the untransposed cipher has the expected amount of non-regional repeating ngrams).
Sounds like a tough problem – I’m glad you are exploring this!
Hi smokie – thanks for your updates. I had been wondering if you were still working on this. Very interesting approach you are taking with rectangular transposition. If Z340 is encoded this way, I’m wondering how you’d be able to determine which scheme is in play. Maybe a specialized hillclimber can look for the untransposition that minimizes the regional biases (i.e., the untransposed cipher has the expected amount of non-regional repeating ngrams).
Sounds like a tough problem – I’m glad you are exploring this!
I am definitely still working on it. These repeats, the ones least likely to occur by random chance, are in the bottom half. So that makes me wonder if there is a regional bias in the bottom half, a different pattern. And if there was, it would be awfully difficult to create so many period 15 / 19 repeats. So even though the patterns are interesting and maybe there is a consecutive rectangle one big transposition that can create pivots, I don’t know if that is what it is.
There is also a spike at period 5. These period 5 repeats, when the message is mirrored, become period 29. So that helps to cause the period 29 spike. Either the pivots are a product of the cipher, or he put them there intentionally as a clue and it is a coincidence that they are at period 29. The pivots increase the period 29 spike as well.
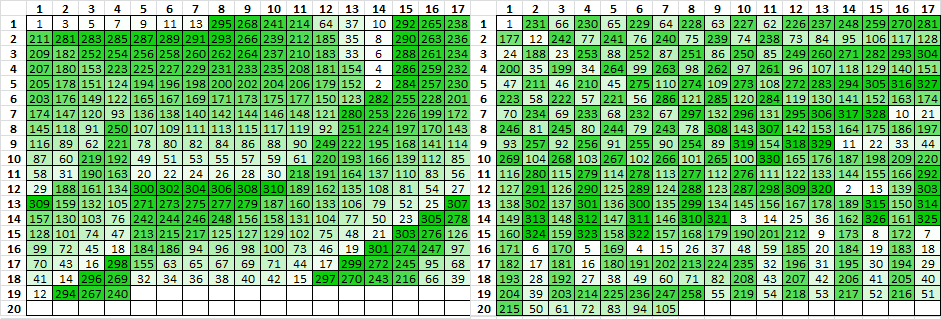
Here is an interesting one. Multiple inscription rectangles 5 x 15 transposed vertically. They create a lot of period 15, 30, and 29 repeats. Period 1 become period 15, period 2 becomes period 30, and period 3 becomes period 29. That is because of the narrowness of the inscription rectangle. The message wraps from column 5 to column 1 the next row down, and transposition causes a lot of period 29 repeats. A few marked in black; spend a few minutes messing around with it to see what I mean.
More posts soon.
I should have shown all of the little inscription rectangles above. This is the general idea. The period 3 bigram marked in blue becomes a period 29 bigram because of the narrowness of the inscription rectangle.
You can start with two column rectangles and increase the number of columns, and the rearrangement of period 1-3 bigrams changes across the graph. The bigrams near the edge of the inscription rectangle get stretched out more and more. Pictures below go from 2 x 15 to 9 x 15 inscription rectangles. Period 1 is blue, period 2 is red, and period 3 is yellow.
The period 110 repeats could possibly be caused by something like this. I will get back to this general idea in a soon future post.
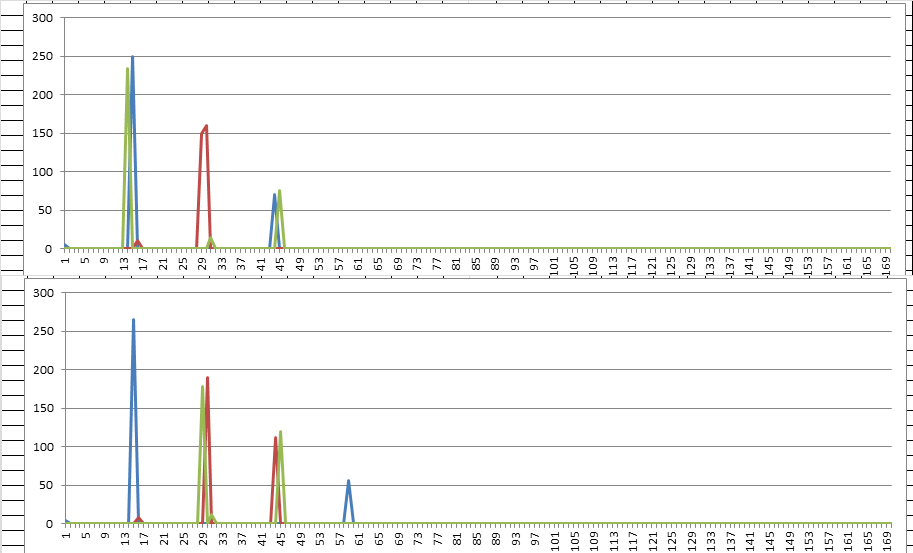
Back to the 5 x 15 inscription rectangles. You would have to start transposition to align things just right to get pivots where the pivots are. The shaded cells show where the pivots are, and only a few of them line up here as period 3 / 29.
More post soon.
Hi smokie!
Nice to hear that you (and others) are still working on z340. I am working on the cipher too but at the moment rather sporadically. I will read your new postings later (I’m at work just now). This morning I had an idea what extra step zodiac may had done and why the cipher can not be cracked. As soon as I am sure that my idea is not stupid I will post it here.
Largo
Hi smokie!
Nice to hear that you (and others) are still working on z340. I am working on the cipher too but at the moment rather sporadically. I will read your new postings later (I’m at work just now). This morning I had an idea what extra step zodiac may had done and why the cipher can not be cracked. As soon as I am sure that my idea is not stupid I will post it here.
Largo
Largo, I have some ideas about how a route transposition could cause a coincidence count spike, which I will explain shortly.
I could also create period 19 with a spike where period 3 becomes period 39 by transposing down right column to left column. The red boxes show a period 3 bigram that would become period 39.
Now… Let’s imagine some double letters, like LL, cut by the edge of one of these inscription rectangles marked in black. That could cause a coincidence count spike. Here, the spike would be at 19 x 4 + 1, or 77. That’s pretty close to 78.
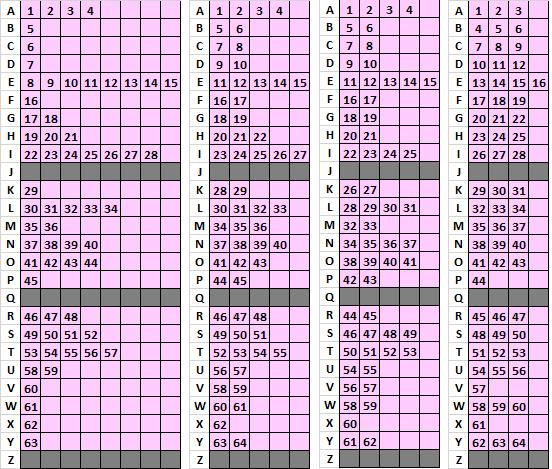
I tried to make some messages with the 5 x 15 inscription rectangles and Jarvle’s 100 message library and 340 like cycle stats, where some of the period 3 bigrams become period 29 bigrams. I have four different efficiency settings for my keys, example below:
Using the least efficient setting, the one on the right, it was still really difficult to match 340 period 29 stats because even period 3 repeats are diffused quite a bit. I made one message that had comparable period 15 / 29 stats, but didn’t save it thinking that I could do it easily again. However, it was not. I found a transposition that makes period 15 / 30 / and 29 bigram repeats, but it was still really difficult to match the 340. I have not tried with the 5 x 19 inscription rectangles. That might improve my odds a little.
It is just that usually only period 1 shows up, if at all, after diffusing a message with about 63 symbols.
However, after all of this, I am starting to get some ideas about transposition detection. With rectangle transposition, there are more tell tale signs than just the period repeats. There is also the period caused by the vertical edges, only with plaintext reversed.
Let’s say for example we have on big inscription rectangle, 20 x 15, and we inscribe left right, top bottom. Then we transpose by taking off the plaintext vertically and transcribing horizontally into a 17 x 20 rectangle. We fill in gibberish or un-transposed plaintext at the end to make 340.
EDITED:
* Depending on diffusion, we may be able to figure out how many columns there were in the inscription rectangle by re-drafting the message into 15 columns so that all of the period 15 repeat symbols line up. Then, compare the top row symbols with the symbols in each row below, offset by one column, and see if a lot of them match up with symbols occurring in bigrams at period 15, only in the reverse order. *
I will work up an example soon.
EDIT:
Here is an example of the above transposition, in plaintext, and redrafted into 15 columns. The idea is to shift rows back and forth one space, and compare two row combinations. The combination / shift that finds the highest number of repeats is the one most likely to reveal the exact shape of the inscription rectangle. The example below compares period 286 reverse bigrams with period 15 bigrams.
I don’t know if it would work on the 340, but it should work on simple transpositions. The old cryptography books use examples of multiple small, usually 5 x 5, inscription rectangle. Maybe the technique could be used to detect multiple inscription rectangles. The general idea is to suspect a transposition, and then look in particular exact locations in the message for certain symbols to confirm.
