I am wondering if you can combine that sort of attack with another one:
For each transposition under consideration, apply it in reverse to Z340, then measure the resulting normal (period 1) ngrams, as well as the even/odd and top/bottom biases. Also measure the IOC of columns vs rows. Then, you can rank the transpositions based on how well they:
1) Increase the number of normal (period 1) repeating ngrams (or cause their quantities to match what we’d expect for a normal homophonic cipher)
2) Remove the even/odd bias and top/bottom bias
3) Match the expected column and row IOCs of normally-enciphered homophonic ciphers.
4) Match other expectations of normally-enciphered homophonic ciphers (not sure what would be in this category yet)
Doing this might help narrow down the possibilities even more, although it seems the large amount of choices to draw from for transposition steps would be prohibitive to a brute force search. It’d be interesting to see how the numbers compare for each type of transposition.
Perhaps you have already done something similar to this in your experiments.
I am wondering if you can combine that sort of attack with another one:
For each transposition under consideration, apply it in reverse to Z340, then measure the resulting normal (period 1) ngrams, as well as the even/odd and top/bottom biases. Also measure the IOC of columns vs rows. Then, you can rank the transpositions based on how well they:
1) Increase the number of normal (period 1) repeating ngrams (or cause their quantities to match what we’d expect for a normal homophonic cipher)
2) Remove the even/odd bias and top/bottom bias
3) Match the expected column and row IOCs of normally-enciphered homophonic ciphers.
4) Match other expectations of normally-enciphered homophonic ciphers (not sure what would be in this category yet)Doing this might help narrow down the possibilities even more, although it seems the large amount of choices to draw from for transposition steps would be prohibitive to a brute force search. It’d be interesting to see how the numbers compare for each type of transposition.
Perhaps you have already done something similar to this in your experiments.
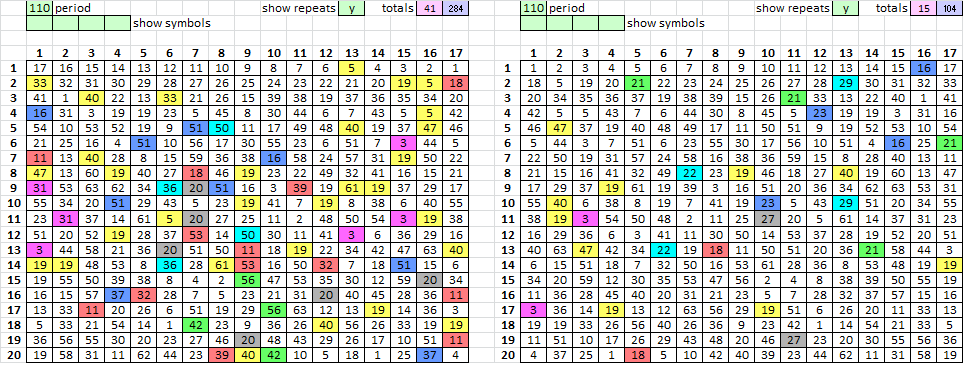
EDIT: The other thing is that there are only 230 possible period 110 repeats to begin with, making the spike more significant.
I haven’t done anything quite that sophisticated. My basic idea is to categorize different types of transpositions, make a list. Then try variations of each on the list and compare, or overlay, with the 340. See if period 1 bigram positions match up. But not just the typical period 1 bigrams that create an obvious pattern, but the non-obvious ones, such as created at the edge of a rectangle, or transition locations between multiple inscription rectangles which would occur at certain intervals. Maybe give special weight to those. And keep trying until finding something that looks more like the 340 than anything else.
Your post about the mirrored period 110 repeats has been in the back of my mind for over a year now. They are similar to the period 29 repeats because they do not appear unless the message is mirrored ( left, mirrored, right regular ). I will have to take a closer look at those to see what they are. 110 doesn’t have to be close to a multiplier of 15 or 19 if there are three rectangles.
EDIT: The other thing is that there are only 230 possible period 110 repeats to begin with, making the spike more significant.
Good point – I hadn’t considered that before. Usually, when I look for periodic bigrams, I allow positions that "fall off" the cipher to wrap around back to the beginning at the first unvisited position. That way I guarantee that all 340 symbols are visited.
My basic idea is to categorize different types of transpositions, make a list.
Have you posted that list somewhere? I want to eventually think about how to generalize that to a transposition function that can explore the space of all such transpositions.
EDIT: The other thing is that there are only 230 possible period 110 repeats to begin with, making the spike more significant.
Good point – I hadn’t considered that before. Usually, when I look for periodic bigrams, I allow positions that "fall off" the cipher to wrap around back to the beginning at the first unvisited position. That way I guarantee that all 340 symbols are visited.
My basic idea is to categorize different types of transpositions, make a list.
Have you posted that list somewhere? I want to eventually think about how to generalize that to a transposition function that can explore the space of all such transpositions.
I have sort of an outline that I started a long time ago. I should probably work on it some more to include different types of diagonal transposition and odd even column transposition.
Nice – thanks for reminding me about the outline. I will plan to circle back to that at some point. I’m taking a neural networks / machine learning course at the moment. For the final project, I hope to build a cipher identification network that will attempt to distinguish ciphers of various types. I’m working from this list at the moment: http://www.cryptogram.org/resources/cipher-types
If the network is successful with the ACA types then I can start adding other types to the list. I’m curious how such a network would classify Z340 (and other unsolved ciphers), especially when all the test ciphers we’ve been collecting here on the forums are included in the training set for the network. Other classification techniques are out there, such as bion’s cipher ID test ( http://bionsgadgets.appspot.com/gadget_ … ended.html) and bion’s neural network ( http://bionsgadgets.appspot.com/gadget_ … ction.html), so there is some really useful work to build from. And the back issues of the ACA periodical are filled with many test ciphers to include in these experiments.
Even if the network fails to classify Z340 (it’s very likely that it won’t classify it), it will serve two purposes: 1) It will be a foundation for adding new cipher types to try to auto-identify them (for instance, the novel transposition schemes you are exploring), and 2) I will have generated a lot of statistics about all the cipher types that could be meaningful to compare to the stats of Z340 and other unknown ciphers.
That sounds like a fun project. I am going to keep working on transposition, take a closer look at the period 110 repeats, and develop more detection tools.
Awesome, I look forward to more reports of your progress!
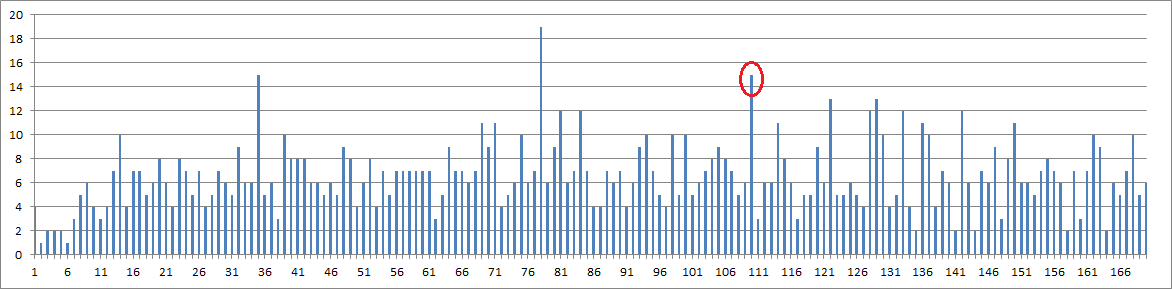
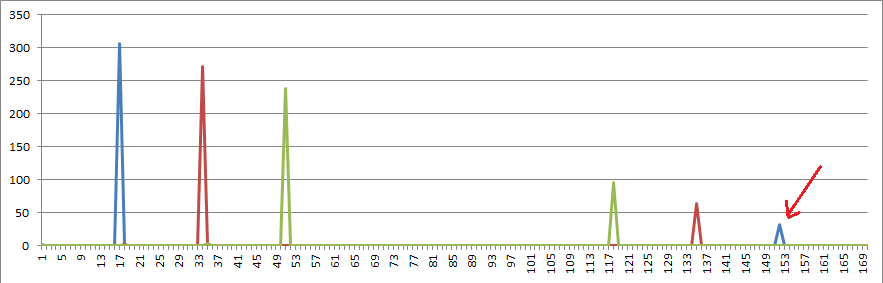
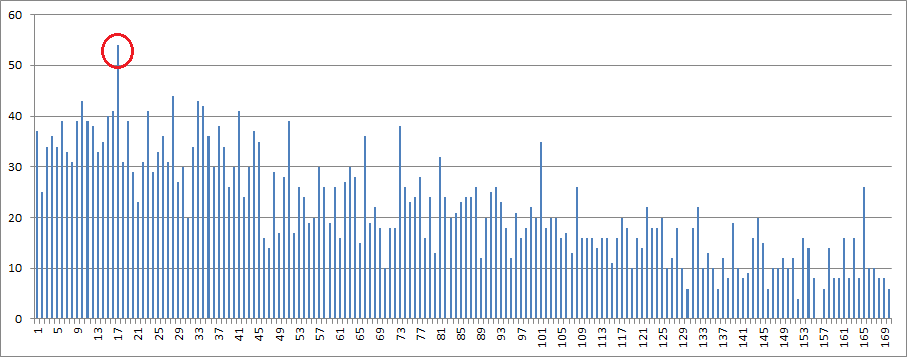
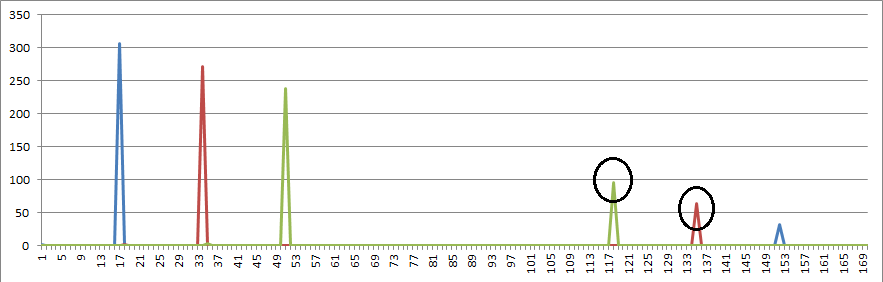
I took another look at the coincidence count column chart. There is a spike at period 110.
Yes, it shows up on BartW’s plot as well: viewtopic.php?p=48147#p48147 (the 2nd plot on that post)
Also, I have a "fragment IOC" measurement that attempts to count the number of repeating fragments (patterns such as A?BC, AB???C, etc), and it gives period 110 the 2nd highest measurement. For some odd reason, it gives period 62 the 1st highest measurement. Has period 62 come up for you before in your analysis?
I need to revisit my fragment IOC calculation to make sure I’m doing it properly and not overcounting anything or making some other mistake like that. It doesn’t give period 1 the highest measurement in Z408 (it shows up 11th on the list). My hunch is that it’s easy to assign repeating fragments too much significance.
I took another look at the coincidence count column chart. There is a spike at period 110.
Yes, it shows up on BartW’s plot as well: http://www.zodiackillersite.com/viewtop … 147#p48147 (the 2nd plot on that post)
Also, I have a "fragment IOC" measurement that attempts to count the number of repeating fragments (patterns such as A?BC, AB???C, etc), and it gives period 110 the 2nd highest measurement. For some odd reason, it gives period 62 the 1st highest measurement. Has period 62 come up for you before in your analysis?
I need to revisit my fragment IOC calculation to make sure I’m doing it properly and not overcounting anything or making some other mistake like that. It doesn’t give period 1 the highest measurement in Z408 (it shows up 11th on the list). My hunch is that it’s easy to assign repeating fragments too much significance.
I have not noticed period 62 for anything. I would guess that the + symbol ( my 19 ) is probably showing up a lot in your repeated fragments. I didn’t work on the 340 much this weekend. I have to take frequent breaks and also time out to think before I decide on a direction to invest my time in.
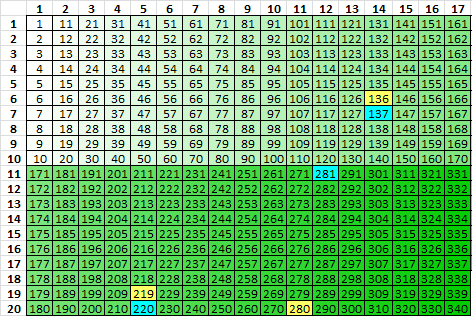
But here is the mirrored 340 redrafted into 55 columns, showing the period 110 repeats. The repeats seems to be clustered into groups of 14-15 columns, separated by three or four columns. May be of no significance, but interesting to me.
I set up a very simple experiment to find out if I could detect the contours of multiple inscription rectangles. Here is how it works, with an example message.
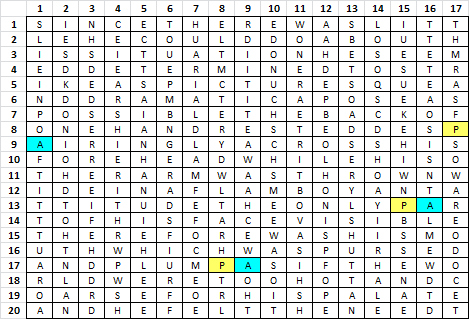
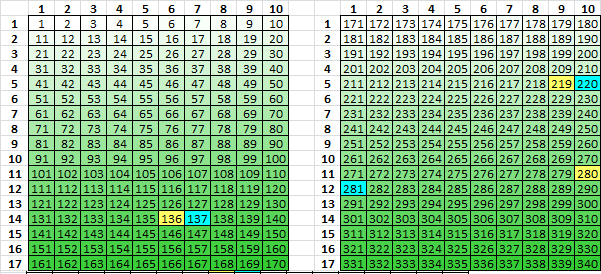
Step 1. This is message # 82 from Jarlve’s plaintext library. Follow the colored bigram P-A through the example. P appears at positions 136, 219 and 280 and A appears at positions 137, 220 and 281.
Step 2. The simple transposition includes two 10 x 17 inscription rectangles. These are the positions. Inscribe left right top bottom.
Step 3. Lift plaintext to transcribe into a 17 x 20 rectangle vertically top bottom left right. These are the positions.
The idea is that most of the bigram repeats are period 17, but some of them are period 152 with the plaintext in reverse order. The bigram repeats P-A that appear at positions 136-137 and 219-220 become period 17. But the bigram repeat P-A at positions 280-281 becomes A-P at period 152 because it is cut by the edge of an inscription rectangle.
Step 4. There are only 32 possible period 152 reverse bigrams, but with the plaintext and diffusion, there will actually be much fewer. These are the ones that the experiment is designed to detect. Scroll right to see them.
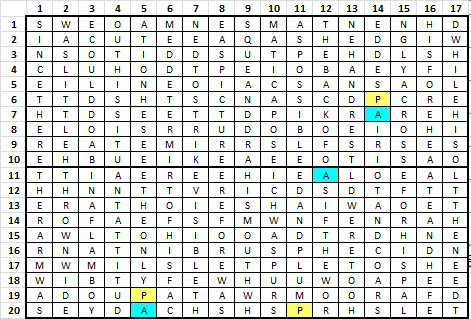
Step 5. Here is the plaintext, transposed.
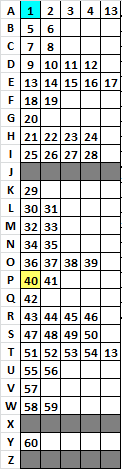
Step 6. Encoded with the following key. Note that symbols 1 maps to A and 40 maps to P, with matching colors.
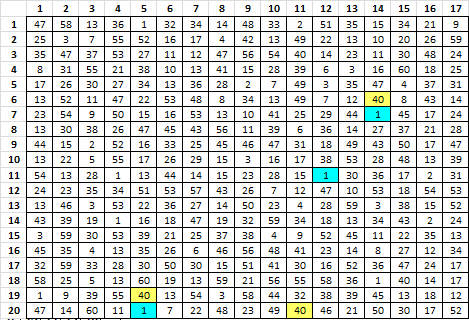
Step 7. Here is the message.
47 58 13 36 1 32 34 14 48 33 2 51 35 15 34 21 9
25 3 7 55 52 16 17 4 42 13 49 22 13 10 20 26 59
35 47 37 53 27 11 12 47 56 54 40 14 23 11 30 48 24
8 31 55 21 38 10 13 41 15 28 39 6 3 16 60 18 25
17 26 30 27 34 13 36 28 2 7 49 3 35 47 4 37 31
13 52 11 47 22 53 48 8 34 13 49 7 12 40 8 43 14
23 54 9 50 15 16 53 13 10 41 25 29 44 1 45 17 24
13 30 38 26 47 45 43 56 11 39 6 36 14 27 37 21 28
44 15 2 52 16 33 25 45 46 47 31 18 49 43 50 17 47
13 22 5 55 17 26 29 15 3 16 17 38 53 28 48 13 39
54 13 28 1 13 44 14 15 23 28 15 1 30 36 17 2 31
24 23 35 34 51 53 57 43 26 7 12 47 10 53 18 54 53
13 46 3 53 22 36 27 14 50 23 4 28 59 3 38 15 52
43 39 19 1 16 18 47 19 32 59 34 18 13 34 43 2 24
3 59 30 53 39 21 25 37 38 4 9 52 45 11 22 35 13
45 35 4 13 35 26 6 46 56 48 41 23 14 8 27 12 34
32 59 33 28 30 50 30 15 51 41 30 16 52 36 47 24 17
58 25 5 13 60 19 13 59 21 56 55 58 36 1 40 14 17
1 9 39 55 40 13 54 3 58 44 32 38 39 45 13 18 12
47 14 60 11 1 7 22 48 23 49 40 46 21 50 30 17 52
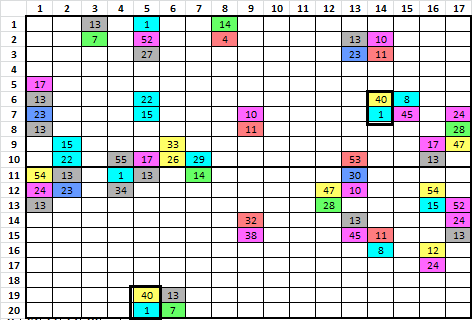
Step 8. O.k. here are the ALL of the period 17 bigrams that have the same symbols as period 152 bigrams, but with symbols reversed. The other symbols are not shown for clarity.
Step 9. Here are ALL of the period 152 bigrams where the symbols are reversed, and match period 17 bigrams.
Step 10. There are only 53 period 17 bigram repeats, not nearly as many as Z340 ( the cycles are approximately 90% perfect rows 1-5, 80% perfect rows 2-10, 70% perfect rows 11-15, and 60% perfect rows 16-20 ).
Step 11. You would think that there would be a small spike at period 152 where the symbols, reversed, have matches at period 17. But unfortunately with these types of messages there are a lot of reverse matches at a lot of periods. There is no noticeable spike at 152, as compared to the other reverse period matches. The red lines are at multipliers of 17, minus 1, showing where you would expect a spike but there usually is not. Scroll right to see the non existent spike.
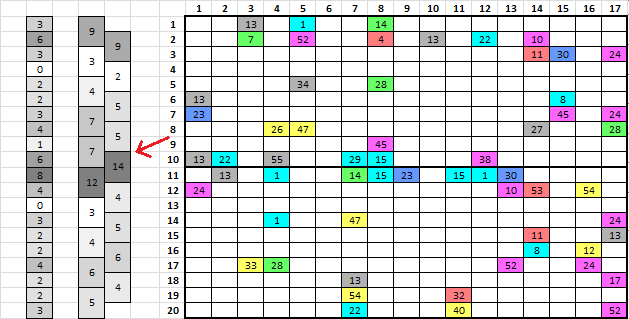
Step 12. However, I found another way to detect the boundaries of the inscription rectangles, without yet going to the probability scores of the repeats. I just summed the count of highlighted cells on each row. Then I summed each combination of side by side rows. Here the sum of the rows 10 and 11 is larger than the sum of any other two rows, showing the boundaries of the two inscription rectangles.
I made 100 similar messages, and the method worked for 64 of them. With the other 36 messages, there were two other rows with more cells highlighted, or there was a tie between rows 10 and 11 and two other rows. So it worked almost two out of three times.
Step 13. I think that the system could be improved by looking for other reverse bigrams that are created by the edge of an inscription rectangle. Period 2 becomes period 34 and reversed period 118, period 3 becomes period 51 and reverse period 135. And so on.
Basically, the idea is that if there are more than one inscription or transcription shapes in the 340, it may be possible to detect their boundaries by finding a path through the message that ties together broken repeating n grams at that boundary.
That is all for this morning.