I’ve noticed that the bigram count of z340 changes little or not at all when you mirror certain parts of the cipher. Example:
On the image above the lines 6 to 11 were mirrored and the bigram count at P1 remained unchanged at 25. I did some simple tests with Peek-a-boo with z340 as well as different ciphers and I had the impression that z340 is somewhat "immune" to mirror operations. So I did the following test (pseudo code):
bigramCountUnmodified = cipherOriginal.getBigramCount();
for (int startX = 0; startX < cipherOriginal.Width - 1; startX++)
{
for (int width = 2; width < cipherOriginal.Width - startX + 1; width++)
{
modifiedCipher = cipherOriginal.MirrorColumns(startX, width);
bigramCountModified = modifiedCipher.getBigramCount();
difference = abs(bigramCountUnmodified - bigramCountModified);
}
}
So I made a slide through the cipher and mirrored all possible regions (always for the whole height). The absolute bigram count difference was determined and summed up. At the end of the test, the average distance to the unmodified cipher was determined as a scoring value (as a percentage of the bigram count of the unmodified cipher). At z340, the average bigram count difference is exactly 8%.
Now I took a long plaintext (Moby Dick from Project Gutenberg) and did a total of 100000 tests with it. At each test a 340 character section was taken out of the book, homophonically encoded and scored with the same method as described above. The average bigram difference is 21.7%. Only 0.949% of all attempts were at 8% or less.
So it looks like z340 is above average "immune" against mirror operations. This test was performed four times with different options. It was tested with different randomness during substitution and also transposed P19 before substitution. These are the results:
Period | Cycle | Avg. Distance | Number of Tests with <= 8%) Test 1: P1 | 100% cyclic | 21,7 | 949 Test 2: P1 | 25% random encoding | 21,0 | 1215 Test 3: P19 | 100% cyclic | 14,75 | 5220 Test 4: P19 | 25% random encoding | 14,8 | 6992
A period transposition thus seems to reduce immunity. (Actually no wonder, because the test runs for the final cipher on P1).
I did the same test one more time, but this time I did the slide not horizontally, but vertically. In this case, the difference is still there, although much smaller. The average deviation at z340 is 12%. So I only did one of the four tests:
Period | Cycle | Avg. Distance | Number of Tests with <= 8%) Test 1: P1 | 100% cyclic | 19,53 | 14884
I don’t know exactly what to do with it yet. It is interesting to note that z340 seems to be above average immune to mirror operations. Maybe someone can repeat the test to make sure I didn’t made any measurement errors.
Next I will examine the reference ciphers, which are below 8% and behave like z340. One assumption is that they have an unigram that appears above average (plus symbol) just like z340.
Also remarkable: If you mirror columns 7 to 15 in z340, P19 disappears and the peak is at P1 (33 bigrams, 4 trigrams). Obviously a phenomenon like P19 can also be generated by a simple mirror operation.
HERabcGTLfIePVdgh Nb+BjkKonmYWDlOpq BrstM+ukLqjWGZUHJ SbbvdcR++ObxVowKg yzM+u143+PF7Ih2e5 bwRdFcgaFeCho-ODj k7+KQlumVGXtUg8LI jGgJp29+uYNy+OkLz hnM+0+#ArtBFgRZ4K -ucUV+BFnvbO+Jdr- U+R571MT0bBYDIEKO gntcRJ3+mM4T7oIBF u#zSrk8jtBF7IN+wR cGFNdp14Vtm04g7++ rBXfos7ZUVaECz4-+ ItmxuBQMpmdbOjKGg RtT+LfIBWcF+nC#qL ++qWCuj5THSOPtWqb IFehWn-oBOYyB1vCt aMDHNbKIAwOZuSe8+
What do you think?
Translated with http://www.DeepL.com/Translator
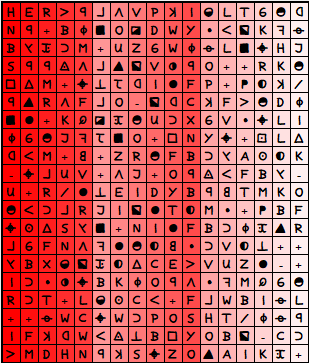
Okay, it gets abstruse. Have a look at the following cipher. It’s from the book "Moby Dick" and can be solved by AZDecrypt without any problems:
;;aFxI:Xrnho23kLp yFdwb2+81cB0=ICsX QPGNpfzugaYxVKF3D Hl2iLMwpZ8I=tOvy+ OS0EYPnGTfdoTj5U: gXFYaVtTxD1T23liz J=hAEXqlcspK=;ylC ukn+;57hMe0RbPoZ9 XrNFc1L=;d2DljYCY flp5eFhwzga;xB2iH cAC8KslXvM3o4=Np9 GZ5qykFh1IX+zd7BK =XL20HpcMo=SUlFPR lflgVakCtxbw:TD8s nieN3BLXw2y1u+0Y5 AJGhEJPV8pfzst=qE QZYXn7=lbX;YUgNa: TIcuUCRJLFxe=AwGd b83H2X:y5s4+EDqN= L0uUrYX7ph;FP9Vfi
Like z340, this cipher is quite "mirror immune". For z340 the average difference is 8%. For this cipher it is only 6.25%.
This cipher has been substituted 100% cyclically and has 63 unigrams. It has 16 repeated bigrams on P1 and 25 on P4. It also has a low IOC compared to z340 (raw 1818). Let’s just imagine that AZDecrypt couldn’t solve it. So we’d probably focus on the peak P4 right away (admittedly, that’s a bit easy thinking. But I’d like to address a general problem if we rely too much on statistics and anomalies).
Now we make a very small change and swap only the last two columns:
;;aFxI:Xrnho23kpL yFdwb2+81cB0=ICXs QPGNpfzugaYxVKFD3 Hl2iLMwpZ8I=tOv+y OS0EYPnGTfdoTj5:U gXFYaVtTxD1T23lzi J=hAEXqlcspK=;yCl ukn+;57hMe0RbPo9Z XrNFc1L=;d2DljYYC flp5eFhwzga;xB2Hi cAC8KslXvM3o4=N9p GZ5qykFh1IX+zd7KB =XL20HpcMo=SUlFRP lflgVakCtxbw:TDs8 nieN3BLXw2y1u+05Y AJGhEJPV8pfzst=Eq QZYXn7=lbX;YUgN:a TIcuUCRJLFxe=AwdG b83H2X:y5s4+EDq=N L0uUrYX7ph;FP9Vif
Now you have 14 bigrams on P1 and 27 bigrams on P10. So it’s an even clearer difference to the previous cipher. Since only two columns were swapped, AZDecrypt should find a solution via the transposition solver. However, this is not the case. I tried it with a stack size of 3 and 1. Both didn’t lead to any success (each waiting about 20 minutes). So I did the same experiment with the first 340 characters of z408. Again, the transposition solver did not exceed 20980 points. However one could recognize the plain text nevertheless clearly. Maybe I was too impatient at this point.
In the next step I used the feature "Columnar Rearrangement" (width 17). If you take the first 340 characters of z408 and swap the last two columns, the correct solution is found in a very short time. However, this is not the case with the Moby Dick cipher shown above. AZDecrypt seems to get stuck.
Jarlve: I know you won’t see this as a criticism of AZDecrypt. I want to make it clear, however, that this is not about talking AZDecrypt down.
My guess:
We know that there are ciphers that have a "natural" bigram peak other than P1, even if no transposition has been done. On some of these ciphers, the bigram distance between P1 and Pn is extremely high. If a very simple transposition is performed on such a cipher, the misleading peak can outmaneuver an autosolver.
What’s wrong with the idea that it’s the same with z340? Maybe P19 is a pure coincidence? I am so bold as to make an assumption without having a test result in my hand: I bet the P10 peak of the cipher shown above is "Higgs-Boson significant". And as shown, still completely wrong.
If I am all wrong, have a thinking error or use AZDecrypt in a wrong way, please correct me. Basically, I’d be almost happy if my gibberish is nonsense. Because if P15/P19 is really nothing special anymore, then we would have lost a strong indicator.
Translated with http://www.DeepL.com/Translator
Referring to the first post, I am not sure exactly what to think. You mirrored all possible contiguous ( next to each other ) groups of columns, and found that P1 doesn’t change much as compared to Moby Dick homophonic cryptograms that you made, but 5% to 7% of Moby Dick transposition homophonic cryptograms behaved similarly to the 340?
If I read LRTB and find AB, but read RLBT and find a BA, I call that a "cross reverse" bigram. I just made up the term for lack of better word. Could the presence of more or less cross reverse bigrams have anything to do with your findings, especially when compared to the test messages?
Is there a classical cipher that can cause your findings?
I agree that some other transposition besides simple columnar / route transposition could cause P19. I have suspected P5; some of the cryptography books showed smaller inscription rectangles, 6 x 5, etc.
See the 9th post down here, where I mention P1. With your P1 test messages, there are some that have bigrams that repeat, but both symbols are low frequency. I wonder how a comparison of the frequency of the symbols that are in the bigrams, in light of your testing, shows anything interesting.
What the post does not show is a distribution graph of the probability scores of the P19 repeats.
I am watching. Thanks.
Referring to the first post, I am not sure exactly what to think. You mirrored all possible contiguous ( next to each other ) groups of columns, and found that P1 doesn’t change much as compared to Moby Dick homophonic cryptograms that you made, but 5% to 7% of Moby Dick transposition homophonic cryptograms behaved similarly to the 340?
Per mirror operation, the percentage bigram difference is measured and summed up. For z340 8% difference is measured. With the 100k testciphers, this difference averages 21.7%. Altogether 0.949% of them behave similar to z340.
If I read LRTB and find AB, but read RLBT and find a BA, I call that a "cross reverse" bigram. I just made up the term for lack of better word. Could the presence of more or less cross reverse bigrams have anything to do with your findings, especially when compared to the test messages?
Is there a classical cipher that can cause your findings?
A very good question. I could imagine that snake routes could do something like that. But I haven’t tried it yet.
See the 9th post down here, where I mention P1. With your P1 test messages, there are some that have bigrams that repeat, but both symbols are low frequency. I wonder how a comparison of the frequency of the symbols that are in the bigrams, in light of your testing, shows anything interesting.
I’ll check it out.
Now you have 14 bigrams on P1 and 27 bigrams on P10. So it’s an even clearer difference to the previous cipher. Since only two columns were swapped, AZDecrypt should find a solution via the transposition solver. However, this is not the case.
The transposition solver does not support that operation. I am planning an update to the solver sometime and then a superficial search for swapped columns could be included. Not sure if I want to add it though.
In the next step I used the feature "Columnar Rearrangement" (width 17). If you take the first 340 characters of z408 and swap the last two columns, the correct solution is found in a very short time. However, this is not the case with the Moby Dick cipher shown above. AZDecrypt seems to get stuck.
This solver still needs allot of work which may happen next year. I solved it by setting columns to 17, search depth to 1 and bigrams to 0.
Jarlve: I know you won’t see this as a criticism of AZDecrypt. I want to make it clear, however, that this is not about talking AZDecrypt down.
No, it is okay. With a transposition search space of 340! there’s really no end to what the 340 could be. Nothing can handle that.
We know that there are ciphers that have a "natural" bigram peak other than P1, even if no transposition has been done. On some of these ciphers, the bigram distance between P1 and Pn is extremely high. If a very simple transposition is performed on such a cipher, the misleading peak can outmaneuver an autosolver.
That is why AZdecrypt has the option to turn off the use of bigrams for its transposition solvers.
What’s wrong with the idea that it’s the same with z340? Maybe P19 is a pure coincidence? I am so bold as to make an assumption without having a test result in my hand: I bet the P10 peak of the cipher shown above is "Higgs-Boson significant". And as shown, still completely wrong.
Low ioc example cipher and it is not Higgs-Boson significant but I think we all realize that the period 19 bigram peak in the 340 is possibly an outlier. And that is why we also work on other things. I try to think in terms of most likely. You first look for things were they are most likely to be. I guess period 19 is pretty high up that list.
The transposition solver does not support that operation. I am planning an update to the solver sometime and then a superficial search for swapped columns could be included. Not sure if I want to add it though.
If two adjacent columns are swapped, it is the same as a mirror operation. I thought AZDecrypt could also perform transposition operations on certain rects, or am I wrong?
Full rectangles only.
Sorry if I’m annoying right now, but I don’t quite understand it. With a 17×20 cipher, the last two columns also form a rectangle (start_x: 16, width: 2, start_y: 0, height: 20). Am I wrong?
It does not perform transposition operations on any sub part of the cipher. The rectangle (in whatever dimensions) must contain all of the cipher.
Thank you. I was just a bit confused, because the output window of AZDecrypt for example says "Mirror (103*4)". I thought they were indexes or something like that.