I want to work on Alberti ciphers more.

Could you give a simple explanation of how this type of encoding works? Thanks.

Sure.

1. Transpose the plaintext
2. Put the Alberti disk on a setting
3. Encode the top third of the message
4. Rotate the Alberti disk to another setting
5. Encode the middle third of the message
6. Rotate the Alberti disk to the same setting as step 2
7. Encode the bottom third of the message
8. Encode again with homophonic symbols

There will be a lot of homophonic symbols that only appear in the top and bottom third of the message, and some symbols that only appear in the middle third of the message.

That’s one example. But there are a lot of different variations. Alternate two settings odd rows even rows, or do that by columns. Or, maybe some other way.

I like it because it is a Renaissance cipher, like the homophonic cipher, and appears next to discussion of homophonic ciphers in some cryptography books.

I also like it because it would allow easier distribution of homophonic symbols on the homophonic key, since there would probably be 26 Alberti symbols to map to instead of like 22 or 23.

The Alberti disk symbols look just like letters, and different combinations of rotations would produce different frequencies of these symbols and mutually exclusive symbols. I wonder if some variation of Alberti encoding before homophonic encoding could produce some of the strange phenomenon.

Fuzzy idea for now.

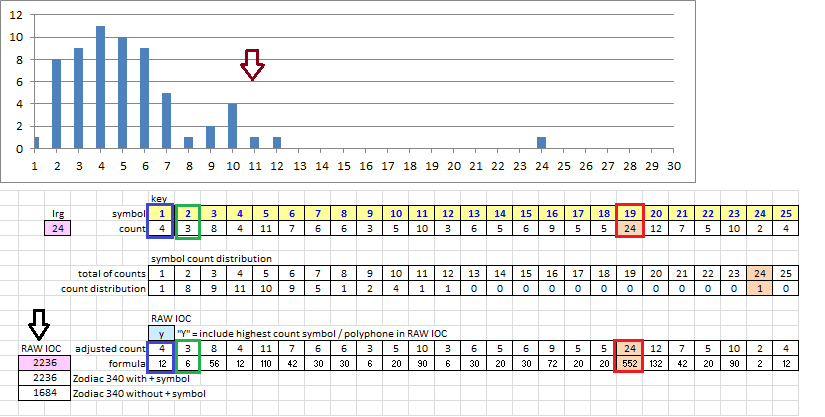
Largo: See below. I use numbers for symbols because I use a spreadsheet, but it is the same.

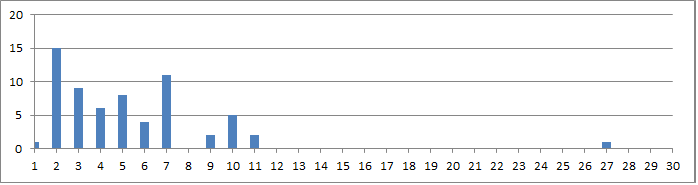
1. The symbol count distribution for the 340. X axis is the count, and Y axis is the number of symbols with that count.
2. Red box, symbol 19, the + has count of 24. The raw IOC value is 24 * 23 = 522. Note that this increased the raw IOC for the 340 quite a bit.
3. Blue box, symbol 1, has a count of 4. Raw IOC value is 4 * 3 = 12.
4. Green box, symbol 2, has count of 3. Raw IOC value is 3 * 2 = 6.
5. Black arrow, sum of all raw IOC values = 2236. It gives us an indication of the shape of the symbol count distribution.
6. Brown arrow. Note that there is a group of symbols that have a higher count than the others. Some of these symbols do not cycle well with others.

Now let’s say I want to encode the first 340 letters of the 408, the I like killing message, and use perfect cycles to keep things simple. And I map one of the ciphertext to three letters so it is a polyphone that may simulate the +. And I use a very efficient key that diffuses high frequency letters as much as possible.

The message:

I L I K E K I L L I N G P E O P L
E B E C A U S E I T I S S O M U C
H F U N I T I S M O R E F U N T H
A N K I L L I N G W I L D G A M E
I N T H E F O R R E S T B E C A U
S E M A N I S T H E M O S T D A N
G E R O U S A N I M A L O F A L L
T O K I L L S O M E T H I N G G I
V E S M E T H E M O S T T H R I L
L I N G E X P E R E N C E I T I S
E V E N B E T T E R T H A N G E T
T I N G Y O U R R O C K S O F F W
I T H A G I R L T H E B E S T P A
R T O F I T I S T H A T W H E N I
D I E I W I L L B E R E B O R N I
N P A R A D I C E A N D A L L T H
E I H A V E K I L L E D W I L L B
E C O M E M Y S L A V E S I W I L
L N O T G I V E Y O U M Y N A M E
B E C A U S E Y O U W I L L T R Y

The very efficient key:

A 1 2 3 4
B 5
C 6
D 7
E 8 9 10 11 12 13 14 15
F 16
G 17 18
H 19 20 21
I 22 23 24 25 26 27 28 8
J
K 29
L 30 31 32 33 34 8
M 35 36
N 37 38 39 40
O 41 42 43 44
P 45
Q
R 46 47 48
S 49 50 51 52
T 53 54 55 56 57
U 58 59
V 60
W 61
X 62
Y 63
Z

The cryptogram:

22 30 23 29 8 29 24 31 32 25 37 17 45 9 41 45 33
10 5 11 6 1 58 49 12 26 53 27 50 51 42 35 59 6
19 16 58 38 28 54 8 52 36 43 46 13 16 59 39 55 20
2 40 29 22 34 8 23 37 18 61 24 30 7 17 3 35 14
25 38 56 21 15 16 44 47 48 8 49 57 5 9 6 4 58
50 10 36 1 39 26 51 53 19 11 35 41 52 54 7 2 40
18 12 46 42 59 49 3 37 27 36 4 31 43 16 1 32 33
55 44 29 28 34 8 50 41 35 13 56 20 8 38 17 18 22
60 14 51 36 15 57 21 8 35 42 52 53 54 19 47 23 30
31 24 39 17 9 62 45 10 48 11 40 6 12 25 55 26 49
13 60 14 37 5 15 56 57 8 46 53 20 2 38 18 9 54
55 27 39 17 63 43 58 47 48 44 6 29 50 41 16 16 61
28 56 21 3 18 8 46 32 57 19 10 5 11 51 53 45 4
47 54 42 16 22 55 23 52 56 20 1 57 61 21 12 40 24
7 25 13 26 61 27 33 34 5 14 48 15 5 43 46 37 28
38 45 2 47 3 7 8 6 8 4 39 7 1 8 30 53 19
9 22 20 2 60 10 29 23 31 32 11 7 61 24 33 34 5
12 6 44 36 13 35 63 49 8 3 60 14 50 25 61 26 30
31 40 41 54 17 27 60 15 63 42 59 36 63 37 4 35 8
5 9 6 1 58 51 10 63 43 59 61 28 32 33 55 48 63

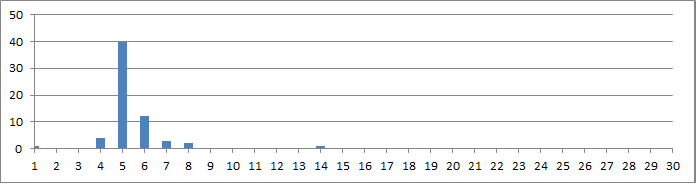
The symbol count distribution, with a raw IOC of only 1628. It’s lower than the 340 because with the 340 there are more symbols with a higher count. It doesn’t look anything like the 340.

O.k., now I will make the key less efficient, but same with everything else.

A 1 2 3 4
B 5 6
C 7 8
D 9 10
E 11 12 13 14 15
F 16 17
G 18 19
H 20 21 22
I 23 24 25 26 27 11
J
K 28 29
L 30 31 32 33 11
M 34 35 36
N 37 38 39 40
O 41 42 43
P 44 45
Q
R 46 47 48
S 49 50 51
T 52 53 54 55
U 56 57
V 58 59
W 60 61
X 62
Y 63 64
Z

23 30 24 28 11 29 25 31 32 26 37 18 44 12 41 45 33
13 5 14 7 1 56 49 15 27 52 11 50 51 42 34 57 8
20 16 56 38 23 53 24 49 35 43 46 11 17 57 39 54 21
2 40 28 25 11 30 26 37 19 60 27 31 9 18 3 36 12
11 38 55 22 13 16 41 47 48 14 50 52 6 15 7 4 56
51 11 34 1 39 23 49 53 20 12 35 42 50 54 10 2 40
19 13 46 43 57 51 3 37 24 36 4 32 41 17 1 33 11
55 42 29 25 30 31 49 43 34 14 52 21 26 38 18 19 27
58 15 50 35 11 53 22 12 36 41 51 54 55 20 47 11 32
33 23 39 18 13 62 44 14 48 15 40 8 11 24 52 25 49
12 59 13 37 5 14 53 54 15 46 55 21 2 38 19 11 52
53 26 39 18 63 42 56 47 48 43 7 28 50 41 16 17 61
27 54 22 3 19 11 46 11 55 20 12 6 13 51 52 45 4
47 53 42 16 23 54 24 49 55 21 1 52 60 22 14 40 25
9 26 15 27 61 11 30 31 5 11 48 12 6 43 46 37 23
38 44 2 47 3 10 24 8 13 4 39 9 1 32 33 53 20
14 25 21 2 58 15 29 26 11 30 11 10 60 27 31 32 5
12 7 41 34 13 35 64 50 33 3 59 14 51 11 61 23 11
30 40 42 54 18 24 58 15 63 43 57 36 64 37 4 34 11
6 12 8 1 56 49 13 63 41 57 60 25 31 32 55 48 64

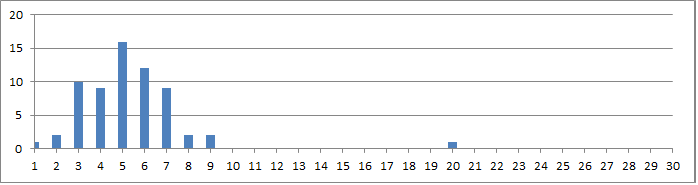
Raw IOC is 1866. It looks a lot more like the 340, but notice that there are more than 15 symbols with count of 5. The peak is higher in the middle than the 340 peak and there are no symbols with count of 10, 11 or 12 like with the 340.

I’ll make the key less efficient again. Just a little bit less efficient.

A 1 2 3 4
B 5 6
C 7 8
D 9 10
E 11 12 13 14 15
F 16 17
G 18 19
H 20 21
I 22 23 24 25 11
J
K 26 27
L 28 29 30 31 11
M 32 33
N 34 35 36 37
O 38 39 40 41
P 42 43
Q
R 44 45
S 46 47 48 49
T 50 51 52 53
U 54 55
V 56 57
W 58 59
X 60
Y 61 62
Z

22 28 23 26 11 27 24 29 30 25 34 18 42 12 38 43 31
13 5 14 7 1 54 46 15 11 50 22 47 48 39 32 55 8
20 16 54 35 23 51 24 49 33 40 44 11 17 55 36 52 21
2 37 26 25 11 28 11 34 19 58 22 29 9 18 3 32 12
23 35 53 20 13 16 41 45 44 14 46 50 6 15 7 4 54
47 11 33 1 36 24 48 51 21 12 32 38 49 52 10 2 37
19 13 45 39 55 46 3 34 25 33 4 30 40 17 1 31 11
53 41 27 11 28 29 47 38 32 14 50 20 22 35 18 19 23
56 15 48 33 11 51 21 12 32 39 49 52 53 20 44 24 30
31 25 36 18 13 60 42 14 45 15 37 8 11 11 50 22 46
12 57 13 34 5 14 51 52 15 44 53 21 2 35 19 11 50
51 23 36 18 61 40 54 45 44 41 7 26 47 38 16 17 59
24 52 20 3 19 25 45 11 53 21 12 6 13 48 50 43 4
44 51 39 16 11 52 22 49 53 20 1 50 58 21 14 37 23
9 24 15 25 59 11 28 29 5 11 45 12 6 40 44 34 22
35 42 2 45 3 10 23 8 13 4 36 9 1 30 31 51 20
14 24 21 2 56 15 27 25 11 28 11 10 58 11 29 30 5
12 7 41 33 13 32 62 46 31 3 57 14 47 22 59 23 11
28 37 38 52 18 24 56 15 61 39 55 33 62 34 4 32 11
6 12 8 1 54 48 13 61 40 55 58 25 29 30 53 44 62

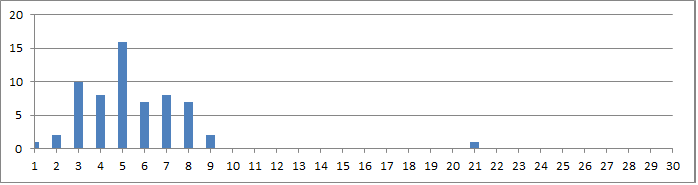
Some of the symbols now have higher count, raw IOC is 1982 and it looks a little bit more like the 340.

Now for a very inefficient key.

A 1 2 3
B 4 5 6
C 7 8 9
D 10 11 12
E 13 14 15 16
F 17 18 19
G 20 21 22
H 23 24 25
I 26 27 28 13
J
K 29 30 31
L 32 33 34 13
M 35 36 37
N 38 39 40
O 41 42 43
P 44
Q
R 45 46 47
S 48 49 50
T 51 52 53
U 54 55 56
V 57
W 58 59 60
X 61
Y 62 63 64
Z

26 32 27 29 13 30 28 33 34 13 38 20 44 14 41 44 13
15 4 16 7 1 54 48 13 26 51 27 49 50 42 35 55 8
23 17 56 39 28 52 13 48 36 43 45 14 18 54 40 53 24
2 38 31 26 32 33 27 39 21 58 28 34 10 22 3 37 15
13 40 51 25 16 19 41 46 47 13 49 52 5 14 9 1 55
50 15 35 2 38 26 48 53 23 16 36 42 49 51 11 3 39
20 13 45 43 56 50 1 40 27 37 2 13 41 17 3 32 33
52 42 29 28 34 13 48 43 35 14 53 24 13 38 21 22 26
57 15 49 36 16 51 25 13 37 41 50 52 53 23 46 27 32
33 28 39 20 14 61 44 15 47 16 40 7 13 13 51 26 48
14 57 15 38 6 16 52 53 13 45 51 24 1 39 21 14 52
53 27 40 22 62 42 54 46 47 43 8 30 49 41 18 19 59
28 51 25 2 20 13 45 34 52 23 15 4 16 50 53 44 3
46 51 42 17 26 52 27 48 53 24 1 51 60 25 13 38 28
12 13 14 26 58 27 13 32 5 15 47 16 6 43 45 39 28
40 44 2 46 3 10 13 9 13 1 38 11 2 33 34 52 23
14 26 24 3 57 15 31 27 13 32 16 12 59 28 33 34 4
13 7 41 35 14 36 63 49 13 1 57 15 50 13 60 26 32
33 39 42 53 21 27 57 16 64 43 55 37 62 40 2 35 13
5 14 8 3 56 48 15 63 41 54 58 28 34 13 51 47 64

Raw IOC is at 2414, higher than with the 340, but that is largely because of one symbol with count of 27. But it doesn’t look like the 340, a lot of symbols only have count of two, but there are symbols with counts of 11 and 12 sort of like the 340.

The raw IOC that is closest to the 340 is the third message, and the symbol count distribution looks more like the 340. But not exactly. Maybe we could find another way to describe the symbol count distribution, but we will not be able to match the 340 exactly without the actual plaintext and key.

Less efficient keys make more P1 repeats because higher frequency letters are diffused less, and therefore the higher frequency bigrams in the message are diffused less.

The raw IOC that is closest to the 340 is the third message, and the symbol count distribution looks more like the 340. But not exactly. Maybe we could find another way to describe the symbol count distribution, but we will not be able to match the 340 exactly without the actual plaintext and key.

I am not sure what you are trying to say but I proposed using the ioc to approximate the repeat potential of the 340. If you want the approximate the symbol distribution then use the chi-squared test.

The chi-squared test is used to determine whether there is a significant difference between the expected frequencies and the observed frequencies in one or more categories.

Thanks for cluing me in on that.

Thanks for the great explanation smokie! I agree with you that a badly chosen key can cause phantom spikes in the raw ioc. Somehow I doubt that Zodiac has bothered to optimize a key based on its plain text. I’d rather think he made it by rule of thumb. That would at least explain the frequent occurrence of the plus symbol. The plus symbol could also be a polyphone (as you have shown in your examples). One of my suspicions for the frequent occurrence is a pattern that he has built in before transposition. For example, a crosshair of + symbols. The problem is that we have very little material to analyze.

I am not sure what you are trying to say but I proposed using the ioc to approximate the repeat potential of the 340. If you want the approximate the symbol distribution then use the chi-squared test.

I think I still have a little trouble understanding the difference between "repeat potential" and "symbol distribution", I’m going to read myself a little bit more and browse through the forum. If I have any questions, I’ll get back to you.
But that didn’t stop me from adding the raw ioc to my statistics tool. You can now set a threshold value. Only encryptions exceeding this value are logged. Here are two examples from the book "Frankenstein" which my tool found:

38 Bigrams, Period 1, raw ioc 2296:

FadnkL2xbG3DjhAEX
I;TB=XViocI1=;yXq
+07HPZQ=rtfkwX=Yg
RC8zXIs:T5Nna;9ux
BIG=;p3dHLXI=XwhI
yU8DYV+K0Asc;PqN=
IlFXCLliMZ7kl5o2f
Bw=tXv1g=RaXI8pxY
3dzDAsKlF=Hly:Nhq
ieXLwZJ+7=8IdnIGX
;;cR04SsClDM=QPVb
X;f9TN2goaA1iL5=q
XIpxuYU3zK7yMo1=X
Iw+RI0:8hAItcEFsI
ruknPZ;zl2fqT=vC7
Qd5RgABaDQXSGN=IU
TIVX;iqh;Yx7HcRJk
ZAE3tdqBlDKn=XLyH
w=8p+MYXsYG0oP7N:
TCFfiVkL2g1=rRBXI

High Unigram Count (22), Period 1, raw ioc 2278

LFabX;YdAh=qTXr9x
ow=lclC:uOv58s237
yhEp4XSnF=Xk=I;DR
iABHl+U:Z1cN;dTe2
Dqb0C7LpP;XzwKiQZ
Jf=IYudegM;TaQ5UY
Do1hXRzlc:uFiQxIU
3kI=GCK2Z:u;y+8l5
spMT;YdNFT;TUhI0l
c:uIUXlOrCPL:TDli
TZAB5q;THTh7E;=;f
Rwoc12duUAX8bvVzg
;T;DjatpCKl=nkMFi
BZosGdqJx3IIyeNSY
X7;+5b=;YD1zhXRiL
0H2c;ZAkK=;PwC;fM
Ig:8dl5opsXe=q1Xu
aFh;9rNl2x7cU=Xj3
BvY=RpC;lFyA5zDlL
2+Ih:wpT;iKM8FZs;

I have uploaded the new version and added two books from Project Gutenberg (was not sure if I am allowed to redistribute, so I read the license first.):
https://www.dropbox.com/s/mcsng1nkzgd3c … 7.zip?dl=0

Largo.
Is there the possibility of selecting certain row and column (ignoring the center) and rotates it ?? !!

I’m learning how to handle your great program. Seeing the transforming cipher and seeing the n-grans statistic is pretty cool.
I’ve done these "spins" on ciphers with "off set rectangular chain" on AZD.
Marcelo

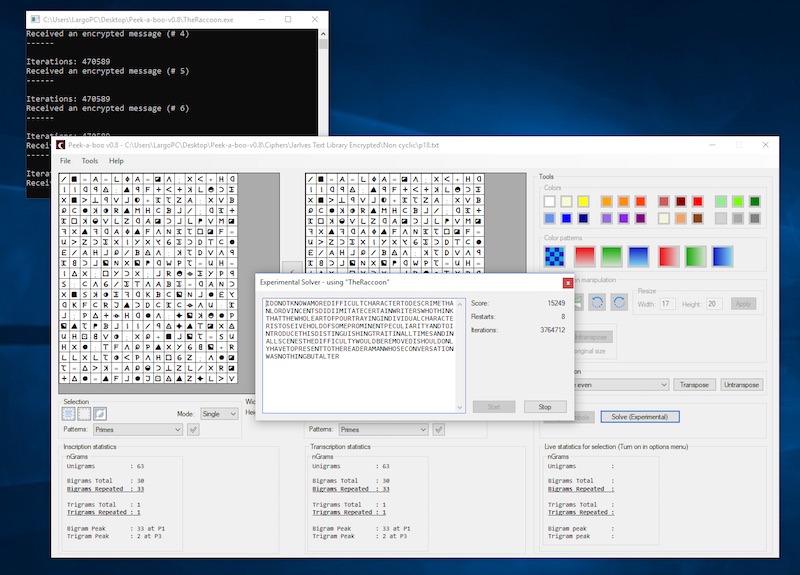
New feature: Solver module
I implemented an experimental solver that can solve homophonic encryption. Not as good as AZDecrypt, but quite passable. In order for Peek-a-boo to solve encryptions, the application TheRaccoon.exe must be running in the background (included in the download folder).

Many thanks at this point to Jarlve, who gave many valuable tips and answered my questions.

Note: If you start the solver, Windows asks for network permissions. This is necessary because peek-a-boo and the solver communicate via network protocols. (Some antivirus programs recognize this as a threat)

Now click File->Load… and load any encryption. Then click on Solve (Experimental) and then on Start. Now the solver should start.

New feature: Merge Symbols
Select two different symbols in the transposition window (ctrl-click) and click "Merge Symbols". Now all affected symbols are replaced by a single one. (For example, if A and B are selected, all B are replaced by A)

New feature: Doublets marker
In the Patterns drop-down, select Doublets. All consecutive symbols are marked.

New feature: Randomization in Encryption.
If you encrypt plaintext, you can now use a slider to set how random the cycles should be.

New feature: Mark rows/columns with no repeats
In the pattern drop-down, select "Mark rows without repeats" or "Mark columns without repeats" and click on the check mark. Now all rows/columns are selected that do not contain repetitions.

Known bugs and problems:
It can happen that Peek-a-boo does not close all processes on quit. I could not fix this bug yet. In this case, simply open the taskmanager, show the processes and quit Peek-a-boo.

Have fun with the new version. If you have any ideas, suggestions for improvement or bug reports, please let me know!

Download at: https://www.dropbox.com/s/y5wvzlbkjdvv7 … 8.zip?dl=0

Translated with http://www.DeepL.com/Translator

Nice update Largo.

Your solver, The Raccoon is working really well.

– Peek-a-boo does not load ciphers where, for example, the last row is a few characters shorter.

Thank you Jarlve!

Currently two types of ciphers can be loaded: Either all symbols in one line, or a "rectangular" format in which each line is separated by a newline. In the latter case, all lines must have the same length for now. At this point I was a bit lazy, I admit;)
Thanks for the hint, I will fix this in the next version. For now please remove linebreaks and put all symbols in one line or add some filler symbols.

I added some more features to Peek-a-boo:

Adjustable IP address of the solver
You can now freely choose the IP address of the solver. I tested it on the local network, but it should also work over the Internet. In this case port 5555 must be open. Theoretically you should now be able to run the solver on a computer in Australia and get the result in Iceland . Of course the results are obtained slower when the solver does not run on localhost.

Paste ciphers from the clipboard
Copy a text or cipher and then click in Peek-a-boo into the inscription or transcription window. Then just press Ctrl+V. Now the content of the clipboard is inserted as a new cipher. The copied text must either be on a single line or all lines must have the same length. I will fix this restriction later.
Of course, you can also simply select a rectangular area in Peek-a-boo, then press Ctrl+C and then paste again using Ctrl+V. This is how you can trim the current cipher.

Vigenere Encode / Decode Dialog
Not a solver, but a convenient tool to create or decode Vigenere Ciphers. First load a plain text and then select Tools -> Encode / Decode Vigenere. Now enter a key and click Encode or Decode.

Shuffle
Nothing special. Just added a "Shuffle" Button to…uhm…shuffle the cipher. (The order of the letters is changed, the distribution remains the same)

Quadgram highlighting
Quadgrams can be highlighted by the corresponding option in the "pattern" dropdowns.

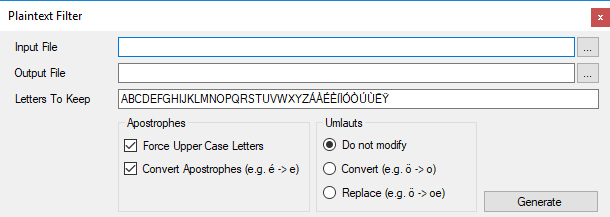
Plaintext filter
Often you have large plain text files, such as free books from Project Gutenberg. These must first be prepared before being used as statistical material (filter out special characters and punctuation marks, convert everything to capital letters, convert umlauts and apostrophes). Now there is a nice tool for that:

Select in the main menu "Tools -> Plaintext Filter" to open up the tool. It should be self-explanatory. Otherwise feel free to ask.
I’ve used it a lot on my own, but I can’t rule out bugs. So take a close look at the result before you work with it.

The next version may be a while in the making. Currently I am at version 0.9 and want to use this opportunity to clean up the user interface and make it more logical. Major refurbishment work is therefore required. But then I will release a new, shiny Version 1.0 =)

Download: https://www.dropbox.com/s/wz3hhi3wc7y9a … 9.zip?dl=0

Have fun!

Translated with http://www.DeepL.com/Translator

Good work Largo.

Sometimes when copy-pasting a rectangular area it adds tabs between the letters. And sometimes it does not.

d	F	c	O	-	o	h	C	e	F	a
K	Q	l	8	g	U	t	X	G	V	m
J	p	2	k	O	+	y	N	Y	u	+
+	0	+	Z	R	g	F	B	t	r	A
U	V	+	d	J	+	O	b	v	n	F
5	7	1	E	I	D	Y	B	b	0	T
c	R	J	I	o	7	T	4	M	m	+
S	r	k	+	N	I	7	F	B	t	j
N	d	p	7	g	4	0	m	t	V	4
f	o	s	4	z	C	E	a	V	U	Z
x	u	B	K	j	O	b	d	m	p	M
+	L	f	#	C	n	+	F	c	W	B

thanks for the bug report. Unfortunately, I cannot reproduce it, this error has never occurred. Does this happen by chance, or can it be reproduced? For example, cipher size x*y, selection start at x1, y1, end at x2, y2?
I tested it with your example, it worked without any problems. Strange…