I don’t believe Nick’s second challenge cipher is vulnerable to simply throwing it in AZdecrypt and blindly running an 8-gram model against it. It is 13% shorter with only 83 letters instead of 108. This causes a small, but significant jump in raw multiplicity from 0.49673 –> 0.53389.

However, I believe it’s quite possible that someone working with pencil and paper could work out some rather large cribs for cipher #2 — ones that would potentially be large enough to solve it from there with AZdecrypt + 8-grams.

Note that the 1st and the 10th line are identical:

116 215 315 400 500
116 215 315 400 500

Also, the 4th and 19th line are identical. And the 22nd line shares a tri-gram with them.

119 211 321 411 521
119 211 321 411 521
 x   x  321 411 521

Nick stated when he released his challenge ciphers in 2017 "The start of the message and the end of the message are exactly as you would expect: there is no padding at either end, no embedded key information, just pure ciphertext."

So I don’t think it’s unreasonable to assume that 116 215 315 400 500 is a single, somewhat common word like "THERE" or "THOSE". At the very least, it should be two smaller words like "I HAVE" or "IN THE". I also wouldn’t be surprised if 119 211 321 411 521 turned out to be two very common words like "IS THE" or "IT WAS".

There are other clues in the letter frequencies that could help quite a bit. Because each column uses its own alphabet, the frequency-hiding benefit of using homophones is almost entirely defeated. Here’s the key for the most common symbols in cipher #1:

509 (6): E
313 (6): T
200 (5): E
416 (5): T
310 (4): E
513 (4): O
102 (4): O
408 (4): I
203 (4): O
209 (4): T

A full 90% of the most commonly used symbols are E T O. The 10th is I. Looking at the next 8 most frequent symbols:

213 (3): H
309 (3): O
114 (3): D
401 (3): Y
407 (3): E
103 (3): A
324 (3): S
115 (3): E

Roughly half of those are also E or O too.

Switching back to cipher #2, all of the symbols in the rows I mentioned (except 211) occur 3-5 times, and are in the top 10 most frequestly used symbols. So probably most of them are ETAOIN.

 3   5   4   3   5
116 215 315 400 500
116 215 315 400 500


 4   2   3   5   3
119 211 321 411 521
119 211 321 411 521
 x   x  321 411 521

Note that many cribs couldn’t work together because of the 1 homophone per column rule. So if you assume the first 5 letters are "THERE", you couldn’t also belive the second crib was "IN THE" because 500 and 521 can’t both encode E.

Does anyone have any hunches? Can you guess the likely cribs for these repeated lines or some other part of Nick Pelling’s challenge cipher #2?

116 215 315 400 500
104 223 315 401 516
116 206 319 424 501
119 211 321 411 521
111 213 323 418 500
103 202 323 407 512
119 215 320 403 500
104 204 316 408 500
124 214 313 401 503
116 215 315 400 500
105 201 308 400 525
114 225 316 411 513
100 225 319 406 523
109 215 315 413 503
100 222 310 402 525
110 203 304 411 505
104 222 314 407 504
119 213 323 418 513
119 211 321 411 521
109 214 313 424 501
122 202 311 405 505
101 220 321 411 521
111 215 310 414 524
105 201 319

Very nice work! It is amazing how far along your and Jarl’s efforts have come.

I solved it with AZdecrypt v1.17 using my newest 8-gram model released a few days ago on Christmas. The only modification I made was adding 15 lines of code to restrict the solver to only use one homophone for each of the five columns. The solve for cipher #1 succeeded, but the way I modified the solver to do it is very inelegant since it can quickly lock high-scoring letters into place and then deprives the hill climber of further opportunities to test them in other arrangements. A more well-tuned version of this general solution would merely penalize (but not forbid) repeated letters in each column. This would allow the solver to evolve through a less jagged solution landscape and then still eventually arrive at a 1-homophone/column solution in the end. I predict this sort of modification would likely solve cipher #2 and beyond.

I am wondering if the penalization factor could have its own temperature gradient, just like the acceptance probability for worse solutions.
For example, at the beginning when the temperature’s high, penalization for violating the column homophone limit is extremely rare.
But as the temperature increases, so does the probability that penalization will occur when violations are detected.
Or, penalization itself could be inversely proportional to the temperature (little to no punishments at first, then gradually apply stronger punishments)

I am curious if such an approach has benefits for the "exploration vs greedy search" tradeoff for search constraints in general, so you have a more dynamic fitness function instead of a bunch of hard-coded constraints.

You guys are doing some really amazing work jarlve and beijinghouse!

If possible could you please share the high-level details of how the entropy-based solver works? I’m familiar with the IoC-based approach and assume it works in a similar manner as far as penalizing the n-gram score. I would assume that the solver favors high entropy in the plaintext over low entropy, such that low entropy penalizes the n-gram score more? Or is it something different entirely?

I suggest you three sources to read.

You may study the code from AZDecrypt from the source code that Jarlve kindly is publishing, see viewtopic.php?f=81&t=3198

Another good study is zkdecrypto, accessible at https://github.com/glurk/zkdecrypto

Both above work similar, with scoring ngrams depending on their logarithmic probability multiplied by an exponential of their length, and penalty to strong deviations from the language’s expected IoC and entropy to prevent converging to e.g. a ngram high score sequence of "THE" with unrealistic IoC and entropy, and combining these in a scoring formula that has heuristically proven to work well in the cases attempted. Optimization is done in hillclimbing algorithm, with an annealing to avoid getting stuck in local maxima.

As third source, here is a link to a Hidden Markov Model used to decrypt 408 and a fake 340: https://scholarworks.sjsu.edu/cgi/viewc … d_projects, as well worth to read.

I appreciate your reply f.reichmann. I have also written a Java project which successfully solves the z408 using a strategy like you described ( https://github.com/beldenge/Zenith ). Currently I am only using n-gram probabilities and IoC. I am not using entropy however, so I was more curious how that could be implemented to improve such a solver.

I tried to read your code, but do not really get at what point you combine the ngrams log probability sum, and the IoC.

For both of AZDecrypt and zkdecrypto, I personally dislike the heuristic formulae in them: They both sum up log probabilities of ngrams, which gives advantage to the most frequent ngrams, which in English are combinations like THE, in particular when popular 2-grams are embedded in 3-grams (HE is in THE). So that this left alone converges to a as much as possible repitition of THE in one string. To prevent the effect, the solution is forced to stay close to the expected IoC, entropy and chi^2. Look eg at the zkdecrypto-lite code, which without the GUI around it is a bit easier to read than the original zkdecrypto (copied from https://github.com/zealdalal/zkdecrypto … r/z340.cpp):

	    score=pentascore+(tetrascore>>1)+(triscore>>2)+(biscore>>3);

    //Stats
    GetFreqs(solv,score_len);

    if(info->ioc_weight) score_mult*=1.05-(info->ioc_weight*ABS(FastIoC()-info->lang_ioc));

    if(info->dioc_weight) //DIC, EDIC
    {
        score_mult*=1.05-((info->dioc_weight>>1)*ABS(FastDIoC(solv,score_len,2)-info->lang_dioc));
    }

    if(info->chi_weight) score_mult*=1.05-(info->chi_weight*ABS(FastChiSquare()-info->lang_chi))/60.0;
    if(info->ent_weight) score_mult*=1.05-(info->ent_weight*ABS(FastEntropy()-info->lang_ent))/150.0;

    //Cribs
    for(int cur_crib=0; cur_crib<info->num_cribs; cur_crib++)
        if(strstr(solv,info->cribs[cur_crib])) score_mult*=(float)1.025;

    return int(score*score_mult);
}

It is not clear to me from the code why 1.05, 60.0, 150.0, 1.025 are good choices. And two effects are pushing in different directions: ngrams counting would by itself not push to the correct solution, it only works because IoC, entropy and chi2 push the ngrams scoring back from running into the outback. But, I confirm, this approach works amazingly well, and thus is justified as an engineered approach, it is allowed to work in real life, without a cool theory behind it (yet).

For above reason, I wrote a code that does without heuristic numbers, counting the ngrams mean and standard deviations, assuming a normal distribution of them, and computing how unlikely the observed string is to be a language. This works, but slower, and at least my implementation without temperature annealing tends to fail solving the more difficult (very uneven homophonic symbol distributions, very bad symbols/cleartext ratio). So that, while I consider from a theoretical point of view more robust, it works less well on the field.

With all my own code, and AZDecrypt and zkdecrypto, and Hidden Markov, all failing to decrypt 340, I believe it makes only limited sense to further study this road. All of the implementations I trust would crack 340 if it was encrypted like 408. The conclusion is, something is different, and the next question is, then how?

There is an inspiring thread about transpositions in this forum, speculating that 340 is transposed before or after encryption, and the symbols are no longer at the position they would be in a text read left-right top-down. Although the investigations are very sophisticated and I sometimes doubt even too sophisticated for a text that was written before personal computers became omnipresent like today, the hoped success is yet pending.

For that, I personally am more theoretically thinking of how to extract from 340, the way it was encrypted. I have two ideas, not implemented yet, but:
1. Go the other way round: Encrypt an encyclopedia in different, guessed and parameterized ways with as few degrees of freedom as possible, and observe if it produces features that resemble 340, as a cipher. Unfortunately, there are endless ways of how to encrypt, and it is hard to find a parameterized encryption factory for me.
2. Speculate that the author did change its encryption, but did not recognize the weakness introduced with following quite strict cycles for the symbols (I mean this bit here: http://zodiackillerciphers.com/wiki/ind … one_cycles). There is cycles in 340, but less, which might match a cycled usage of symbols, with a transposition not completely destroying the cycles. For the algorithm, the task is to break down the symbols into ~26 groups (or less, only frequent letters will cycle nicely), each of which cycle "as good as possible", by transposing the original 340 with as few degrees of freedom as possible (to prevent over-adaptation), and optimize for the symbols in each groups. There is myriads of combinations, so that hill-climbing might be use-full here. If it really is "just" transposed a bit, then this might cast a blurry shadow of how it was transposed, if the speculation should be correct.

f.reichmann i am with you on this

"the symbols are no longer at the position they would be in a text read left-right top-down. Although the investigations are very sophisticated and I sometimes doubt even too sophisticated for a text that was written before personal computers became omnipresent like today, the hoped success is yet pending"

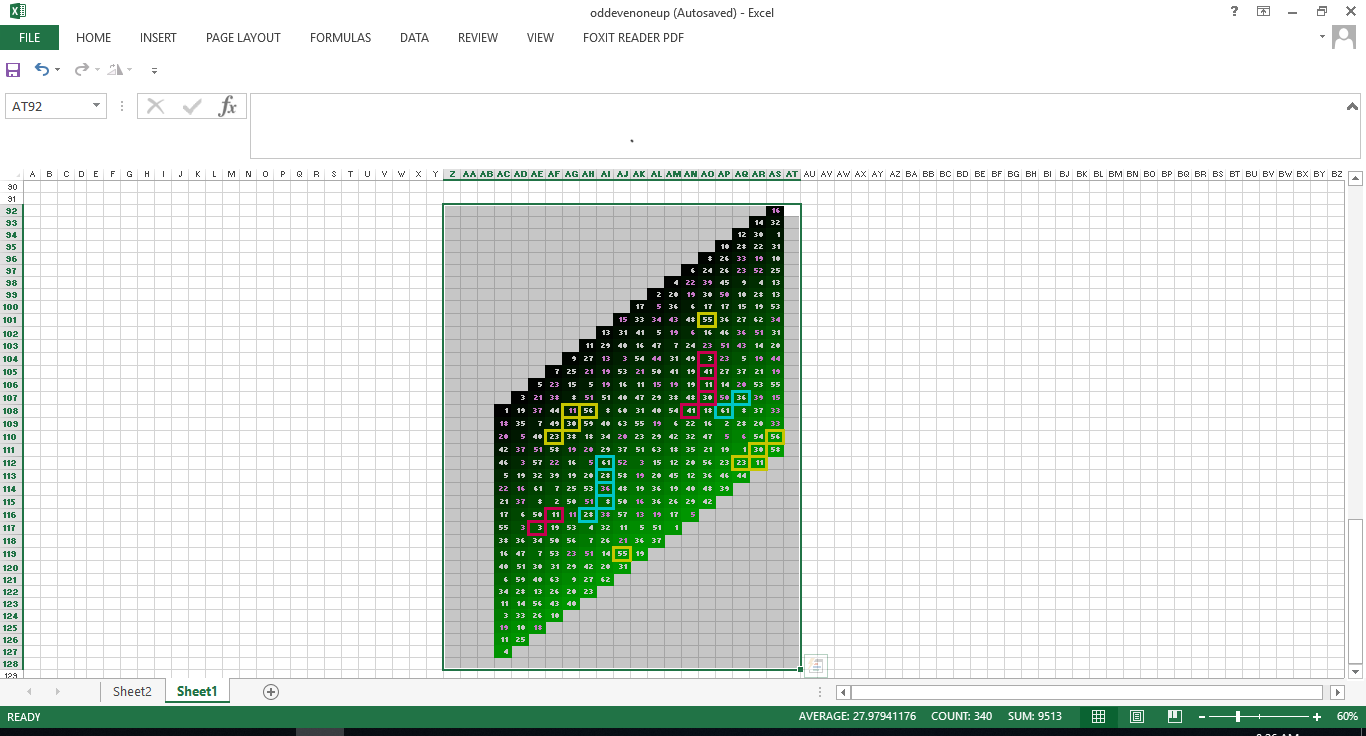
my best guess graph paper, pen and scissors.
write out plaintext, cut into either columns rows or sections (squares or other) rearange rewrite the now jumbled plaintext and then use substitution symbols.
simple and effective.
see above odds evens column shift up one for an example

You guys are doing some really amazing work jarlve and beijinghouse!

If possible could you please share the high-level details of how the entropy-based solver works? I’m familiar with the IoC-based approach and assume it works in a similar manner as far as penalizing the n-gram score. I would assume that the solver favors high entropy in the plaintext over low entropy, such that low entropy penalizes the n-gram score more? Or is it something different entirely?

Here’s the code. It’s roughly implementing a measure of Shannon Entropy.

				for i=1 to l
					enttable(i)=abs(logbx(i/l,2)*(i/l))
				next i

							for i=0 to abc_sizem1
								entropy+=enttable(frq(i))
							next i

l = length of the cipher / text
abc_sizem1 = alphabet length minus 1 -- which is used only because parts of the code use A=1 and others A=0, so this indexes A-Z --> 0-25
frq = frequency

That’s how entropy is calculated. When the solution is updated during a solve, the frequencies are updated to get a new entropy score. There are some wrinkles in the code, but the basics of how it scores is:

Total score = sum of ngram scores * ngram_weight / total_number_of_ngrams * entropy ^ entropy_weight

ngram_weight and entropy_weight are variables set to balance out how much you want each component to contribute to the overall score.

It’s sort of amazing how well both entropy and IoC work. They’re both blind to the underlying letters that make up their frequency distribution. So the entropy score of a text where you swapped every T <–> Z and E <–> X would be identical, even though a text with 25% of the letters being X/Z shouldn’t be seriously considered as an English solution.

I’m surprised no one tries using chi-squared scoring in place of IoC / entropy. But entropy is pretty darn good. Certainly better than IoC for cipher solving.