I have as well implemented a hill climbing and scoring inspired from zkdecrypto, and am trying a chiffre disk (each letter turning the disks by one against each other, with the clear symbols being in different sequence than abcdef), and as well trying shuffling the cipher itself by swaps. So far without results on z340, but reaching convergence on z408, 340 homophonic test ciphers with more than 63 symbols and uneven distributions, and chiffre disks with long texts (1344 characters of Daniel5 excerpt)

The homophonic and the chiffredisk ciphers are converged to the solution by my code if the cipher is long enough. Straight-forward homophonic looks simple, but currently I am not able to make it converge with 340 character chiffre-disk ciphers with freedom of arrangement of the clear text alphabet. The second method of swapping characters in the cipher text to automatically solve the transposition schemes that are posted here in the forum, I conclude as to be quite useless.

The reason is the Unicity Distance, see here: https://en.wikipedia.org/wiki/Unicity_distance . There is some estimates for different encryption methods here: http://practicalcryptography.com/crypta … tatistics/. Obviously, the longer a text, the more the sum of characters resembles that of the standard distribution, the easier it becomes by swapping them around to produce any arbitrary text. Transposing endangers the sense of having a text fundamentally.

Lets just (as we have to expect: falsely!) assume z340 is a straight-forward homophonic cipher, then according to above link, Unicity Distance is 147/100*N – 4991/100 + 9/40*[(2*N+1)*ln(N) – (2*N-51)*ln(N-26)]. On my pocket calculater, at N=63 this equals to 100,15. This means we have 340-100=240 characters of information more to use, before hitting the point of no return in gibberish.

Every of these 240 plain-text carries 4,7 bits of information as per alphabet, minus 1,5 bits of information in meaningful English language because we exactly operate on the difference between gibberish and meaningful, which provisions us with 3,2 bits of information per plain-text character. Means, as soon as we allow transpositions, Vigenère keys, or whatever else in sum to have a freedom of more than 3,2*240=768 bits of information, the result must be expected to turn to random.

Swapping only columns, ln_2(17!) is ln(17!)/ln(2)~=48, so that looks still ok, it is not mathematically impossible for convergence.

Swapping arbitrary characters, ln_2(340!)~=2374, which I tried to automatically attack the transposition schemes in this forum and Feynman2, is deemed to fail. It will converge to the big number of arbitrary texts of length 340 that have an English-conform letter distribution.

Useful operating space is now in between of Unicity Distance plus algorithm inefficiency, and ciphertext length.

Speaking in algorithms, I suggest we keep the amount of freedom in the automatic attacks low (like swapping columns, reversing parts of the text, taking every n-th character as it was done for Feynman1 and proved to be hard to decrypt despite the simplicity), and seek for a response in the score. I expect, if the applied transposition goes into somewhere near the right direction, there would be a signal in rise of the achieved scores. If such a rise can be observed seperate of the statistical noise, it is a starting point to look further into, for confirming or rejecting the assumption that z340 is transposed, or a Vigenère.

The zkdecrypto implementation of hill-climbing greatly depends on rating statistical features of the plain text, and comparing them against English standards. While unfortunately, some numbers look like guess-work or tuning in the code, I think they can be reasoned mathematically following above information theory, Shannon might lead the way here.

Despite that, I believe the zkdecrypto algorithm does not have the power to converge at the Unicity Distance minimum, it needs an algorithm penalty for convergence inefficiency on top. So that another step in coding work shall be to enhance the scoring function and the hill-climbing in zkdecrypto, to converge on as bad as possible ciphertext/unicity distance ratios. A starting point might be to rate and optimise algorithm quality from such a statistic.

A good target to attack could be Feynman2, with a higher level of trust that it really contains something written by a human with intact brains and good intentions.

At http://zodiackillerciphers.com/wiki/ind … servations, there is reports of a signal observed around 78, 39 and 19, which are approximate multiples of each other. We could play with that and speculate on Vigenères at length 19, or Chiffre Disks of size 19 with dropping some rare characters in English.

I’ll publish a github link to my code and some short description in a separate post. I re-wrote in Java.

I have been working for the past month to try to determine whether the 340 was obscured by moving around the columns of the cipher. I have, unsuccessfully, been developing a number of programs to test this theory. The problem is hard to test because there are 17! (3.6 x 10^14) possible rearrangements of the columns. To put that in context, if each core of a processer could run (and score) 100 rearrangements a second, it would take over 110,000 years to run all possible result. Even if you had 100 eight core processers, multiprocessing, it would take 140 years to process every solution. ← I hope my math is right here. To combat this problem, I have come up with a couple of different programs to reduce the time required to arrive at the correct arrangement, but I have had limited success. All of my methods score the ciphers based on n-gram counts and make “decisions” about how to move the cipher based on the resulting scores. Here is what I have done:

Hill Climbing
With this method the program makes switches of columns and will only select an answer if the n-gram count will return a better result. This method works very well with simple scrambles for example for a cipher where the columns 1 and 2 are switched with 16 and 17 the algorithm will find the proper arrangement very quickly – typically within 3000 shuffles. However, when the column moves are very complicated it will not get close to finding the solution.

I made a modified version of this algorithm. It would hill climb until it got the best result. Then once it had gotten the best possible result and capped out on column switches, it would change the arrangement of the cipher and try again. So for example it would swap the sides of the cipher and chug along. Then it would move each column forward one space (so column 0 becomes 1 and 1 becomes 2) and so on. At best, after hundred of thousands of runs and trying the different beginning arrangements, it will only rearrange 8 out of the 17 columns in test cipher’s correctly.

Markov Chain Monte Carlo (MCMC)
I tried two different variations of a MCMC type analysis. In the first, the programs would score the n-grams in the scrambled cipher and then make a random change to the cipher columns. The program with then calculate an n-gram score for the resulting cipher and compare it to the old arrangement (“selector score”). For example assume the original cipher scored a 50 for an n-gram count, if the new cipher scored 60 the program would accept the new arrangement of the columns. Now that the score was 60 it would make another random change. Lets say that change resulted in an n-gram score of 40. The program will divide the new score by the old score (40/60). So then there will be a 67% chance it will accept the new move. Otherwise it will go back to the old arrangement. This method is better because you have to accept bad arrangements to get to other better arrangements. I also tried this by artificially lowering the probability after it was calculated.

The second method was similar to the first but instead of calculating a selector score, it would just assign a flat probability that it would select a bad result.

The problem with this method is that it requires so many cycles through the algorithm before it is possible to get the right result. In theory, this method should get the correct arrangement way before brute force, because it favors better results while allowing it to explore bad result. However, even after running 2,000,000 shuffles the algorithm hasn’t gotten close to solving the test ciphers. I would love to run a billon shuffles, but hard drive space and time are becoming limiting factors.

How it Scores the Ciphers
The ciphers in each method are scored by bigrams, trigrams, tetragrams, and a variety of other combinations for example bigram – random symbol – bigram. I have tried scoring each differently (eg. Trigrams get more points than bigrams ect.) and scoring them all the same with no notable results. When I tested this on the test ciphers the bigram score was good at separating the correct answer from the wrong ones. Of course the program can come up with higher bigrams solution than the correct cipher arrangement, but it is rarely comes up with a better score than the correct arrangement. You can separate out the false ciphers by running them through a cipher solver.

In short, I am looking to pick the community’s brain to see if they have any suggestions to get this moving in the right direction.

Hey Biz:

People have tried what you are trying to do above. But just because there is such a thing a keyed columnar transposition doesn’t necessarily mean that Zodiac did that with the 340 in 17 columns.

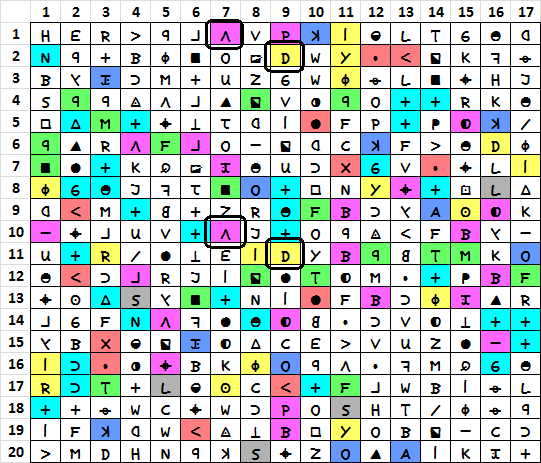
Check this out. There are only six of the < and four of the S, but in the bottom half of the message there is an improbable pattern.

The pattern persists across many positions and symbols. There are only seven colors used below, but use them to find matching symbols with the same pattern. I marked one of them for you with a bold black box so you get the idea.

Biz and f.reichmann, thanks for posting your interesting ideas about automated attacks. I have a hard time committing to specific kinds of automatic solvers since we don’t yet know the ciphering system behind Z340. But, if enough test ciphers are breakable for a particular kind of automatic solver, and Z340 still can’t be broken, then that could constitute good evidence against that particular encipherment hypothesis. "Encoded normally via homophonic substitution" seems to be strongly ruled out in this way.

I really wish we had stronger evidence towards a particular type of encipherment. Then more energy could be invested towards a customized approach, especially if the encipherment method has some unique qualities that aren’t covered by other traditional pen-and-paper ciphers.

Smokie, thanks for your points about the periodic repeating patterns. Here is another way to visualize them:

http://zodiackillerciphers.com/period-19-bigrams/

Go to the "Period 19 scheme" section, and hover over the trigrams and bigrams there. They will highlight in the cipher text.

But, if enough test ciphers are breakable for a particular kind of automatic solver, and Z340 still can’t be broken, then that could constitute good evidence against that particular encipherment hypothesis.

This is the theory behind my endeavors to create an automated column switching program. If I can develope a system to rearrange cipher text and score better rearrangements accurately without having to use a solver, it would be possible to rule out several hypothesis. The way I see it is it is a race to the bottom to rule out or in all logical possibilities. If we can create a method to do that, then eventually — however long that maybe — we can determine wether it is solvable.

That is great – I’m glad you are doing this work. I started a "hypothesis testing" project a while back but stepped away from it because my focus changed:

http://zodiackillerciphers.com/wiki/ind … is_Testing

If you reach a point where you think you’ve strongly excluded a hypothesis, I can add it to that list. I think it will be useful to collect all the tested hypotheses. It is difficult, though, because the tests people are doing and have done in the past have varying degrees of thoroughness and documentation.