Hey smokie,
That must have been allot of work and thanks for your study. I’m trying to analyze it but I ran into some problems with your cipher smokie2017.1. I’m unable to solve it with the transposition matrix you provided and bigram repeats are all over the place, there is no clear indication of direction. Also, do you think you could convert your system to how doranchak and I count bigram repeats or is it your choice by design?
This shows that using an efficient key does not create as many period 19 repeats as an inefficient key and it is likely that Zodiac used an inefficient key.
Yes I agree. I think it is also possible that Zodiac used a key that matched the efficiency of the 408 key and that the homophones were not alternated properly.
What it comes down to for the 340 is that its unigram frequencies are less suppressed than those of the 408. I believe it may connect to the randomization in the encoding (somehow), but if assuming an inefficient key then it does not. When the frequencies become less suppressed ofcourse all plaintext related stats go up.
Maybe I have a bug in my ngram creator. I’ll check that later.
I used the same source. Perhaps you didn’t format correctly. There are always 4 positions preserved for the numeric values. Convert unused positions into spaces or zeros in front of the numeric value. Do not put everything on one line, there’s some limit. Try about 10.000 or 100.000 chars per line.
AZdecrypt can use 5 and 6-grams. The ngram format for 5-grams is as following: "EXAMP1234XAMPL 123AMPLE 12" or "EXAMP1234XAMPL0123AMPLE0012". And for 6-grams: "EXAMPL1234XAMPLE 123AMPLES 12" or "EXAMPL1234XAMPLE0123AMPLES0012". The numeric value is the score of each ngram and cannot exceed 9999.
Here’s my program that creates the list of names from the source files. It randomly picks a male or female name and then adds a last name and loops. I wanted to use the probabilities also but it worked fine without so I didn’t bother.
screenres(800,600,32) type names p as double n as string end type dim as integer i,j,k,a,b dim as integer last_count dim as integer male_count dim as integer fema_count dim as string s,t dim as names last(100000) dim as names male(100000) dim as names fema(100000) open "c:azdecryptnameslast.txt" for binary as #1 do line input #1,s a=instr(s," ") if a>1 then last_count+=1 last(last_count).n=left(s,a-1) end if loop until eof(1) close #1 open "c:azdecryptnamesmale.txt" for binary as #1 do line input #1,s a=instr(s," ") if a>1 then male_count+=1 male(male_count).n=left(s,a-1) end if loop until eof(1) close #1 open "c:azdecryptnamesfemale.txt" for binary as #1 do line input #1,s a=instr(s," ") if a>1 then fema_count+=1 fema(fema_count).n=left(s,a-1) end if loop until eof(1) close #1 open "c:azdecryptnamesnames.txt" for output as #1 for i=1 to 10000000 j+=1 if rnd>0.5 then print #1,male(int(rnd*male_count)+1).n; else print #1,fema(int(rnd*fema_count)+1).n; end if print #1,last(int(rnd*last_count)+1).n; if j>10000 then j=0 print "."; print #1,"" end if next i close #1
I’m unable to solve it with the transposition matrix you provided
Rotate the message 180 degrees and expand symbol 12, which maps to E, I and T. Your solver solved it in less than 1 second one time for me, and less than 3 seconds another time.
bigram repeats are all over the place, there is no clear indication of direction
That is one of the takeaways from the experiment. It is easy to make a message that has x number of period 39 repeats, and then when reading the message in the wrong direction, there is a spike in period 29 repeats. The repeat distribution doesn’t look exactly like the 340; repeat counts are not a clear indication of transcription direction a lot of the time. Spikes in some periods are unreliable, except that the period 15 / 19 spike exits no matter what reading direction. The only spikes that are reliable are the ones that are consistent no matter what reading direction.
Also, do you think you could convert your system to how doranchak and I count bigram repeats or is it your choice by design?
The spreadsheets count them that way, and color shade the cells based on that. Also, I can score the repeats that way better. AB AB AB scores using 3 instead of 2. I don’t think that it really matters though.
The experiment shows that a 5 row distortion significantly reduces the count of period 19 repeats, which is counter to the distortion idea for creating pivots.
I think that the pivots are either a visual clue or a red herring. A game. I am open to the possibility that a cipher created them, and interested in trying to figure one out, but for now calling it as I see it. It was either "gee, they will never figure out that this is a transposition cipher unless I give them a clue, maybe these pivots pointing in these two directions will help them realize what this really is," or "hee, hee, hee, I will put these two pivots in here and that will drive them crazy for years, ha, ha, ha." And it did.
Rotate the message 180 degrees and expand symbol 12, which maps to E, I and T. Your solver solved it in less than 1 second one time for me, and less than 3 seconds another time.
Ok, I was wondering if anything was wrong with the cipher but there isn’t.
That is one of the takeaways from the experiment. It is easy to make a message that has x number of period 39 repeats, and then when reading the message in the wrong direction, there is a spike in period 29 repeats. The repeat distribution doesn’t look exactly like the 340; repeat counts are not a clear indication of transcription direction a lot of the time. Spikes in some periods are unreliable, except that the period 15 / 19 spike exits no matter what reading direction. The only spikes that are reliable are the ones that are consistent no matter what reading direction.
10. This one shows a comparison of period 39 repeats and mirrored period 29 repeats. In group IV, 50 of the messages had more mirrored period 29 repeats than period 39 repeats, even though the message is correctly read left right top bottom. That is because period 5 bigrams that occupy the rightmost and left most columns in a 17 x 20 rectangle, become period 29 bigrams when the rectangle is mirrored.
So, some of the period 5 bigram repeats become period 29 bigram repeats after mirroring the cipher and vice versa? You say first and last column, do you have a visualization laying around by chance?
It would seem though, that mirroring or flipping the 340 is a likely step since period 1 bigrams also increase. What do you think? You have posted allot of stuff and I’ve read it several times and I’m still working on interpreting it.
So, some of the period 5 bigram repeats become period 29 bigram repeats after mirroring the cipher and vice versa? You say first and last column, do you have a visualization laying around by chance?
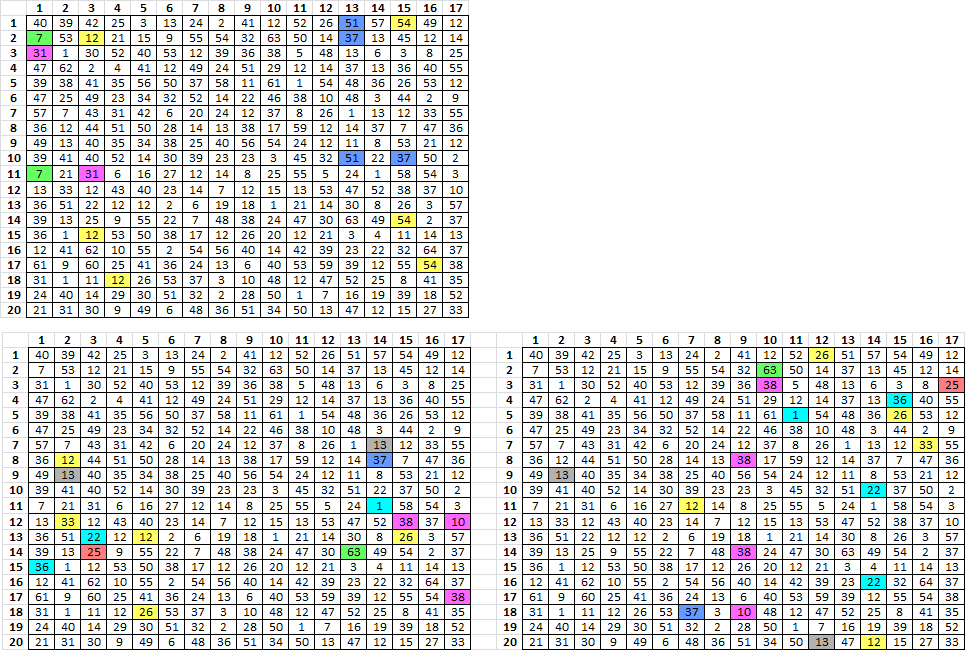
Top left are the period 5 repeats for smokie2017.1 that, when the message is read right left top bottom, become period 29 repeats.
Bottom left are period 5 bigrams that have symbols matching period 39 bigrams at bottom EDIT: right. When the message is read right left top bottom, they all become period 29 repeats. That’s what creates the period 29 spike in smokie2017.1, but it is a period 19 transposition. There are similar bigrams in the 340 which make the period 29 spike.
It would seem though, that mirroring or flipping the 340 is a likely step since period 1 bigrams also increase. What do you think? You have posted allot of stuff and I’ve read it several times and I’m still working on interpreting it.
Not sure what you mean, but smokie2017.1 has the biggest spike at period 1, but it is a period 19 transposition. I don’t know why but it is a little bit scary. I didn’t check all of the periods before posting it, that was just a chance occurrence.
I am just saying that plaintext transcription direction cannot be determined with period x bigram repeats alone. One useful tool is the distribution of bigram repeat scores. For example, you could have the bigram repeat VE, which occurs in the words SLAVE and VERY. But V is likely to only have one substitute, and since E is inefficiently diffused, you could easily have a bigram repeat that scores very high because there are only three V’s in the whole message.
So, score all of the bigram repeats for each period. Then graph the score distribution. The graph with the higher shifted scores combined with the period x bigram repeat count is more likely to be the true period.
Hey smokie,
There are similar bigrams in the 340 which make the period 29 spike.
That’s quite a find then, are you sure there’s no way these bigrams could belong to period 29 somehow?
So, because of mirroring the cipher in a set of dimensions X, Y some period A bigrams transfer over to period B bigrams. It’s really interesting but I’m left with questions. Assuming X=17, Y=20. Are there multiple A’s for every B or vice versa? Does there exist a B for which there is no A? If the last question is no can we then assume and equal amount of *noise* for each period? Or is it that you have detected more noise at A=5, B=29?
I have solved smokie2017.1. I agree that the only period we can be sure of right now is period 15 and 19, but still find the other peaks interesting.
I am just saying that plaintext transcription direction cannot be determined with period x bigram repeats alone. One useful tool is the distribution of bigram repeat scores. For example, you could have the bigram repeat VE, which occurs in the words SLAVE and VERY. But V is likely to only have one substitute, and since E is inefficiently diffused, you could easily have a bigram repeat that scores very high because there are only three V’s in the whole message.
Yes, I know you score bigrams this way and it’s something I haven’t considered yet.
So, score all of the bigram repeats for each period. Then graph the score distribution. The graph with the higher shifted scores combined with the period x bigram repeat count is more likely to be the true period.
I would like to have your system in AZdecrypt, you’ll need to give it a name and tell me the required calculations. If you want to keep it to yourself then that is fine ofcourse.
We need automated noise cancellation. One thing I thought of is for each period to offset the cipher N amount of times and take the average from the offsets, what do you think?
Another thing is to increase the depth, for each period N map out the full periodic bigram range from 1 to cipher length and calculate the total difference from the average (rough explanation). The results then looks like this for the 340 (observe that there is less noise in the depth version, in both images the peak is period 19):
Normal periodical bigrams:

Depth periodical bigrams:

Here’s an update on my language project. Everything is going well, though AZdecrypt will not be able to display unicode because the simple GUI library that I use does not seem to support it. To work around this all languages which require unicode will use a standard alphabet "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijk…" and the .ini files will come with a lookup table:
A = unicode 1080 B = unicode 1081 C = unicode 1082 ...
The main functionality I have planned for these 5-grams is a cipher language identificator inside AZdecrypt that will automatically run through all these languages for your cipher and provide back correlation numbers. Not only will it be good to rule out the 340 will all these languages, but they may also go some way on other unsolved ciphers. I’m interested to see how Voynich and such will correlate.
Here’s the download location for the languages: http://corpora2.informatik.uni-leipzig.de/download.html my criterea was that at least a 1M file was available for the language. That is 1 million sentences or give or take about 100 to 200 megabytes of sentence information. In that respect I downloaded 1M files for all languages to keep the information that goes into each set of ngrams even.
These are the languages that my project will include. After the project is complete I may be able to serve specific language requests given that enough of it can be found on the internet.
african(southafrica) albanian(albania) arabic(wikipedia) azerbaijani(azerbaijan) belarusian(belarus) bulgarian(wikipedia) catalan(catalonia) cebuano(cebuano) czech(czechrepublic) czech(europe) danish(denmark) german(germania) austriangerman(austria) german(switzerland) greek(greece) english(england) english(austria) english(canada) english(europe) english(fiji) english(newzealand) english(unitedkingdom) english(southafrica) esperanto(mixed) estonian(estonia) persian(iran) finnish(finland) french(france) bosnian(bosniaherzegovina) hebrew(wikipedia) hindi(india) croatian(wikipedia) hungarian(wikipedia) armenian(armenia) indonesian(mixed) indonesian(indonesia) icelandic(iceland) italian(mixed) japanese(japan) korean(wikipedia) latvian(latvia) lithnuanian(lithuania) dutch(netherlands) norwegianbokmal(norwegia) norwegian(norwegia) persian(wikipedia) polish(wikipedia) portuguese(wikipedia) portuguese(brazil) portuguese(portugal) romanian(romania) moldavian(moldavia) russian(russia) russian(azerbaijan) russian(kazakhstan) russian(moldavia) slovak(slovakia) slovenian(slovenia) spanish(wikipedia) spanish(columbia) spanish(costarica) spanish(ecuador) spanish(guatemala) spanish(honduras) spanish(uruguay) swedish(sweden) tamil(mixed) tatar(mixed) turkish(turkey) ukrainian(ukraine) vietnamese(vietnam) chinese(china) traditionalchinese(china)
Great work, Jarlve. It will be very interesting indeed to run various ciphers through the language identification feature!
That’s quite a find then, are you sure there’s no way these bigrams could belong to period 29 somehow?
So, because of mirroring the cipher in a set of dimensions X, Y some period A bigrams transfer over to period B bigrams. It’s really interesting but I’m left with questions. Assuming X=17, Y=20. Are there multiple A’s for every B or vice versa? Does there exist a B for which there is no A? If the last question is no can we then assume and equal amount of *noise* for each period? Or is it that you have detected more noise at A=5, B=29?
No, not sure at all. But the experiment shows that it is not particularly difficult to make a period 19 message, read it in the wrong direction, and get a period 29 spike.
There is more than one configuration for each period because bigrams can be split by message borders, and mirroring the message causes the count of bigram repeats to be different for each period. Some period A bigrams transfer over to period B bigrams and vice versa.
I am not sure if it is necessary to eliminate noise. It is just that we are stuck trying to interpret the message in 17 columns and 20 rows as he drafted it, and the only reliable bigrams that we have to work with are the ones that are not split by message borders.
I would like to have your system in AZdecrypt, you’ll need to give it a name and tell me the required calculations. If you want to keep it to yourself then that is fine ofcourse.
I will continue to work in this area, and of course share. I need to work on the above idea some more. Also, I suggest that you score the bigram repeats. Make a distribution chart with repeat score on x axis and count of bigrams with that score on y axis. Do it for period 15 or 19. Then shuffle the message and do it again for the same period. Compare. Shuffle again and again and again and compare. You will see what I mean.
My current feeling is about getting back to basics, detection, and working with transpositions that are not encoded. Just plaintext. Using different ways to analyze plaintext transpositions, such as your symmetry idea, to identify period and transcription direction and nulls. Then move on to encoded messages.
I’m hoping to present everyone’s progress at this year’s crypto symposium (it’s in October). Even if there’s no solution yet, you have all found good clues in the cipher that I hope to expose to a wider codebreaking audience.
Hey doranchak,
I don’t want my work or progress represented at the crypto symposium. The interview earlier last year backfired so much. I’m okay with my work being represented on your websites as long as it is factual. In that regard, could you please change this piece of information in your wiki (you may have missed my last request).
Consider the normal way of counting bigrams (one symbol right next to another). Let’s call this "period 1" bigrams, because the symbols are one position apart. There are 25 repeating period 1 bigrams. But at other periods, there is a higher count of repeating bigrams. In fact, at period 19, there are 37 repeating bigrams. (Illustration of a small sample of repeating period 19 bigrams) (Daikon’s initial observation) (Jarlve’s initial observation)
Either change (Jarlve’s initial observation) to my true initial observation, for that see the quote below. Or change the wording so that it does not reflect an initial observation or remove my observation entry entirely. Thanks.
Nice updates to your wiki and thanks for adding AZdecrypt with it. By the way, my initial observation of the period 15/19 bigrams peak was prior to the one you listed. It is in viewtopic.php?f=81&t=2158&start=20 third post from the bottom.
I am not sure if it is necessary to eliminate noise. It is just that we are stuck trying to interpret the message in 17 columns and 20 rows as he drafted it, and the only reliable bigrams that we have to work with are the ones that are not split by message borders.
I would say that even these bigrams are not reliable since they could as well be random. To only work with bigrams that are not split by message borders seems like a very harsh line to draw, what will you have left to work with then? And what if the cipher once existed in another grid, and the bigrams you interpret as being not split by message borders are split by the other grid?
Also, I suggest that you score the bigram repeats. Make a distribution chart with repeat score on x axis and count of bigrams with that score on y axis. Do it for period 15 or 19. Then shuffle the message and do it again for the same period. Compare. Shuffle again and again and again and compare. You will see what I mean.
Sorry, I don’t get your point.
My current feeling is about getting back to basics, detection, and working with transpositions that are not encoded. Just plaintext. Using different ways to analyze plaintext transpositions, such as your symmetry idea, to identify period and transcription direction and nulls. Then move on to encoded messages.
It’s a good idea. Let me know if you need anything.
I would say that even these bigrams are not reliable since they could as well be random. To only work with bigrams that are not split by message borders seems like a very harsh line to draw, what will you have left to work with then? And what if the cipher once existed in another grid, and the bigrams you interpret as being not split by message borders are split by the other grid?
You are right.
It’s a good idea. Let me know if you need anything.
It would be really nice to have some plaintext route transposition messages to work on. Maybe one with one complete inscription rectangle, message less than 340, a 17 x 20 transcription rectangle and some nulls at one end of the message. One with an incomplete inscription rectangle, message length 340, and 17 x 20 transcription rectangle. And one with more than one inscription rectangles, message length less than 340, and 17 x 20 transcription rectangle with some nulls at one end of the message. You could make only one of them and not tell me which one it is, or all of them and tell me what they are, or whatever you have time for. Or I could make some for you if you want as well. I just need a break from homophonically encoded messages for a while.
It would be really nice to have some plaintext route transposition messages to work on. Maybe one with one complete inscription rectangle, message less than 340, a 17 x 20 transcription rectangle and some nulls at one end of the message. One with an incomplete inscription rectangle, message length 340, and 17 x 20 transcription rectangle. And one with more than one inscription rectangles, message length less than 340, and 17 x 20 transcription rectangle with some nulls at one end of the message. You could make only one of them and not tell me which one it is, or all of them and tell me what they are, or whatever you have time for. Or I could make some for you if you want as well. I just need a break from homophonically encoded messages for a while.
Hey smokie,
All three have been created, though I won’t tell which is what unless asked.
1 2 3 4 5 6 7 2 3 8 9 10 11 11 6 12 12 8 6 5 4 7 13 9 14 2 6 15 16 9 6 6 4 8 17 6 9 5 18 4 3 8 2 12 2 2 11 4 3 17 9 2 16 19 6 4 12 5 12 2 2 7 1 2 15 18 1 20 7 2 21 22 1 4 9 11 3 7 12 8 6 3 15 7 22 19 2 2 18 2 3 1 1 21 4 14 1 14 7 6 7 1 16 3 4 6 7 18 3 15 9 8 9 9 23 7 1 8 9 3 18 10 20 6 1 18 6 1 3 1 4 1 4 6 12 11 24 18 6 6 2 3 5 17 6 2 3 16 17 9 12 7 9 6 19 1 20 14 7 6 7 8 18 8 1 17 12 20 9 8 8 12 7 4 4 8 6 3 12 7 1 3 17 13 2 14 2 10 22 12 2 7 7 12 5 8 1 7 6 14 1 22 16 11 7 4 4 17 7 9 10 15 7 9 20 16 2 2 7 10 5 20 25 17 1 9 2 12 7 1 22 11 7 1 4 6 11 3 2 16 3 16 14 3 1 7 13 3 4 18 14 22 2 3 6 16 6 2 3 6 6 6 11 3 2 13 14 22 17 6 21 8 7 11 18 12 6 5 9 20 6 9 9 18 18 8 6 8 6 5 2 12 4 22 12 18 2 7 12 8 6 18 7 6 2 1 4 14 6 9 4 3 14 9 12 8 7 14 6 3 15 6 4 20 6 16 18 18 3 1 7 3 17 7 15 18 14 7 4 2 1 2 3 4 2 5 6 2 7 5 5 8 9 10 11 7 12 13 8 14 15 4 9 16 13 16 17 4 15 8 10 16 2 18 10 2 13 10 7 18 9 2 13 19 13 11 2 17 11 8 5 5 15 2 5 10 15 10 11 2 2 16 16 4 4 9 11 7 4 16 3 16 8 16 19 4 15 15 16 5 15 7 10 16 17 9 3 16 5 16 13 16 15 18 5 14 16 11 10 11 5 19 9 18 9 15 5 18 8 16 3 6 15 20 18 15 16 16 2 16 15 14 4 4 2 4 5 13 17 10 2 8 13 20 15 15 21 5 14 10 16 11 15 4 10 2 5 9 12 2 16 2 17 4 4 10 5 20 16 16 8 5 11 16 18 9 15 15 5 2 15 17 16 3 14 19 6 17 10 11 9 13 9 18 5 16 5 3 14 3 16 22 11 17 13 4 21 16 10 10 9 11 15 2 13 16 16 5 17 16 4 16 15 18 5 18 16 18 15 4 6 16 13 5 4 9 20 15 9 2 16 16 11 14 21 18 10 15 16 18 15 2 9 16 2 9 7 15 15 16 15 16 15 5 12 5 9 4 4 16 13 7 10 10 17 2 6 12 5 21 21 10 4 16 13 3 21 15 11 5 3 10 5 13 10 15 2 11 21 13 5 16 16 13 10 16 7 16 7 7 16 21 4 13 2 9 18 4 4 4 16 5 5 16 4 16 2 20 9 5 1 8 10 15 5 23 10 16 16 16 19 13 14 15 10 10 6 16 15 16 1 2 3 4 4 5 6 7 8 3 4 5 9 1 10 11 5 7 12 2 8 5 13 14 9 15 15 16 17 5 3 7 15 18 14 17 7 3 5 7 8 7 9 4 19 20 1 19 5 21 4 4 3 21 10 1 3 4 10 2 18 2 4 17 12 6 10 9 8 7 17 4 5 17 4 17 9 5 4 1 17 6 6 15 5 4 10 10 16 4 15 4 22 10 3 4 7 1 9 1 11 15 4 4 21 11 9 12 21 18 1 10 4 8 4 22 1 5 12 15 10 9 10 14 1 11 8 6 8 21 6 1 4 12 5 15 4 8 5 4 3 9 22 4 3 3 4 21 7 12 7 4 4 16 10 10 17 9 9 17 9 5 13 10 4 14 3 4 22 9 5 10 4 22 11 14 7 14 1 4 18 5 1 2 12 10 3 1 2 14 14 4 9 19 2 3 1 2 8 9 14 5 19 4 17 16 5 2 22 2 9 5 4 2 3 8 5 3 10 10 1 9 13 2 12 2 3 14 6 5 11 12 14 20 9 6 22 8 5 5 14 9 4 5 3 16 14 14 14 19 17 9 3 18 6 4 5 18 15 22 1 17 5 5 19 9 20 4 19 11 10 21 13 21 9 4 4 2 22 2 7 11 1 6 9 14 4 2 3 2 10 11 7 8 5 9 12 1 3 12 8 1 8 12 19 2 5 17 12 3 4 18 14 3 5 14 3 11 12 14 20 17 9 5 4 21 2 4 5 19 4 5 5 4 14 5 4 4 9 14
I’ve reworked my encoder so that it can now closely match the raw ioc of the 340. It basicly tries various random keys until it finds one that closely matches a certain value, in this case it is 2236. I will now again look at some basic questions we’ve asked while keeping the same plaintext p1 active with 1000 encoding tests/samples per question.
So under these constrictions,
How much overall cycle randomness in the 340?
Exactly 18%. Very close to what smokie suggested earlier.
This cycle randomization approximation is kept at 18% for all the questions below unless stated otherwise.
Is it possible to match the unigram per row repeats of 18 as seen in the 340?
Yes, the average was 21 and it dipped as low as 10.
Does any of these ciphers match the unique sequence lengths of the 340?
No, the highest one at length 17 had 25 repeats.
How many period 1 bigram repeats with 18% cycle randomization?
49 on average.
Does randomization in the encoding diminish bigram repeats?
Yes, with 0% cycle randomization there were 52 bigram repeats on average.
Then can we assume that when the plaintext does not follow the encoding direction bigrams will be even lower?
Yes, they dropped to an average of 46 with a period 15 transposition.
Is it possible to match 25 period 1 bigram repeats as seen in the 340?
No, the lowest was 33.
While applying period 15 transposition first, is it now possible to match 25 period 1 bigram repeats as seen in the 340?
Yes, the average was 22 with values ranging from 10 to 34.
While applying period 15 transposition first, is it possible to match 34 period 29 bigrams repeats as seen in the 340?
Yes, the average was 21 and the highest 34.
While NOT applying period 15 transposition first, is it still possible to match 34 period 29 bigrams repeats as seen in the 340?
Yes, the average was 22 and the highest 35.
And one more question, still under the same set of rules.
Is it possible to have a symbol with a frequency of 24 with 18% randomization?
No, the highest frequency on average is 15 with a range between 11 and 21.