Plaintext p1 where the letters have swapped places at random for so many iterations.
Does that mean the plaintext is still readable or have too many swaps occurred to preserve readability?
Plaintext p1 where the letters have swapped places at random for so many iterations.
Does that mean the plaintext is still readable or have too many swaps occurred to preserve readability?
Are you shuffling the plaintext to simulate transposition?
Plaintext Cycles
A related subject from a post I made last May in the Homophonic Substitution thread:
*******
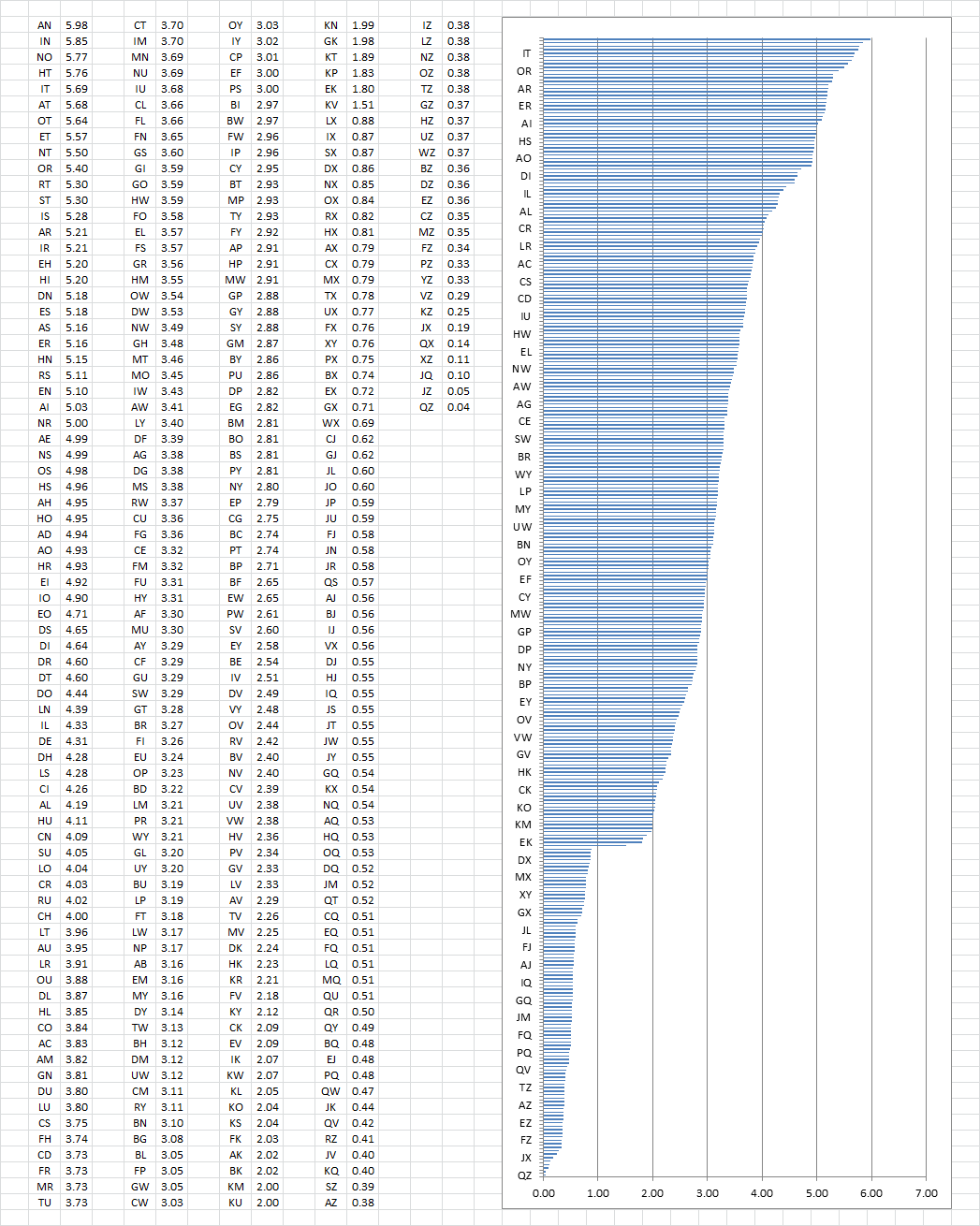
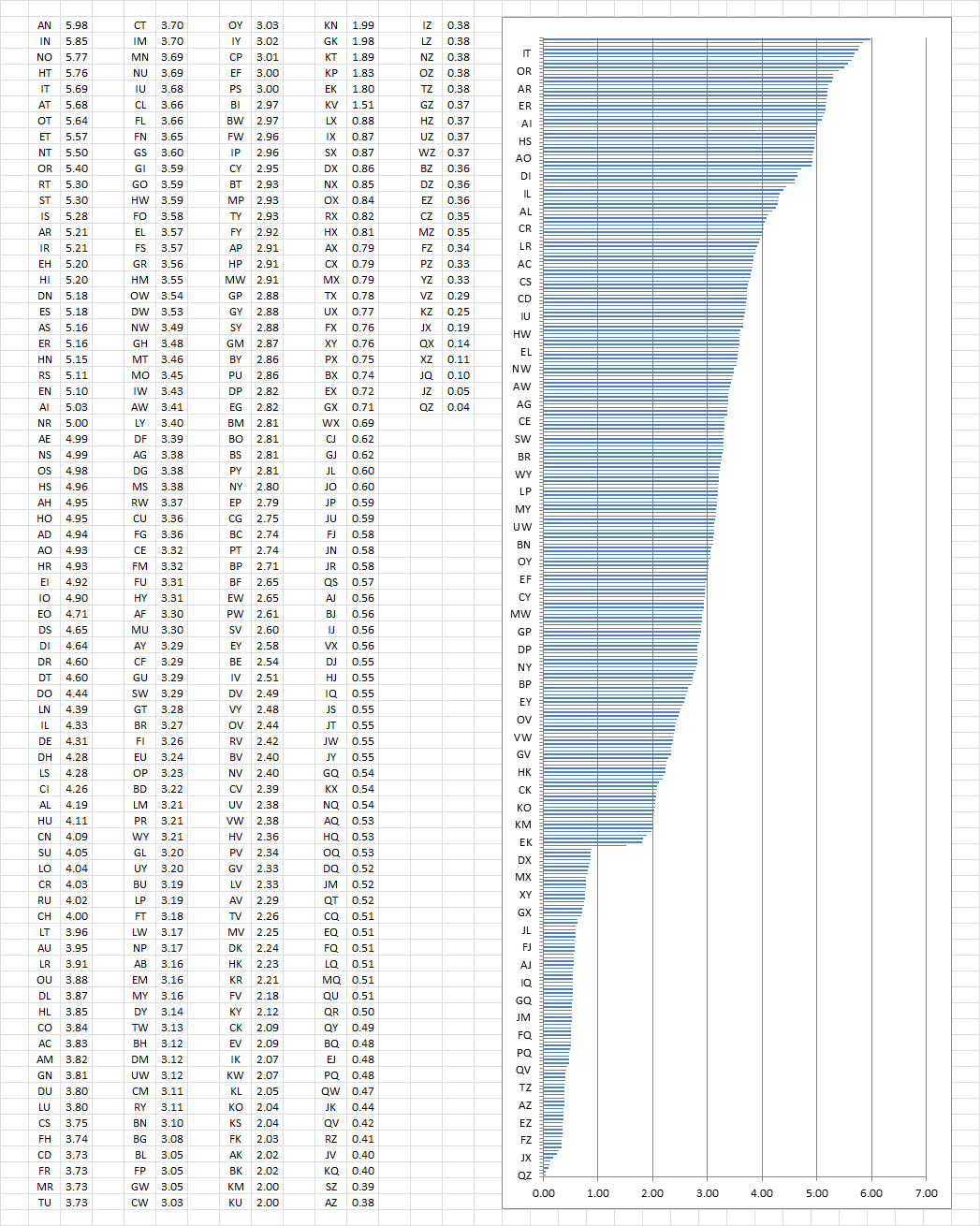
I found all of the plaintext cycles in the Jarlve 100 library, and here are the stats. The number next to the pair of plaintext is the average number of consecutive alternations across all 100 messages. The bar chart is very condensed, and doesn’t show all of the plaintext pairs. But it does have a distinct shape, with a peak and high area near the top, and a sudden drop where certain plaintext like X are included.
Some plaintext pairs cycle with each other more than others. The plaintext pairs don’t necessarily show the first order. In other words, plaintext pair AN could have a cycle that starts with A or N.
The top three are AN, IN and NO. Note that all include N.
The next group of six are HT, IT, AT, OT, ET, and NT. Note that all include T.
The next group of six are OR, RT, ST, IS, AR and IR. There are a mix of R, S and T.
It occurs to me that plaintext included in high frequency bigrams are close to the top, such as AN, HT ( TH is the same thing ), and ET ( TE is the same thing ). And plaintext that often appear in pairs, such as L, aren’t close to the top because a pair destroys a cycle.
Now I am wondering. Is a false cycle is a plaintext cycle that shows up as two ciphertext that are members of two different homophonic cycle groups, and which just happen to be cyclically encoded so that the plaintext cycle can be detected?
Probably not. The cyclic encoding of the homophonic cycle groups doesn’t have to correlate perfectly with the plaintext cycle. The cyclic encoding of the homophonic cycle groups can skip over parts of the plaintext cycle, if there even is one. I think that when we are looking at false cycles, we are probably looking at two plaintext that don’t cycle together, but look like they cycle together because of the homophonic cycles.
I will do a little more experimenting soon. I am just wondering if false cycles and true cycles have slightly different characteristics with regards to the spacing between ciphertext. Is there a way to tell the difference?
*******
Then I looked at periodical bigram repeats and found something interesting that I don’t know what to make of it. I want to consider it a loose observation for now. On top you have the transposed periodical bigram repeats with a peak at 18 (this is similar to untransposed period 19 btw). And on the bottom it is the same with "2z" merged into 1 symbol (cycle assumed). After doing that transposed period 78 peaks with 39 bigram repeats.
I wanted to reproduce this observation. Here are my numbers, do they look the same as yours?
https://docs.google.com/spreadsheets/d/ … sp=sharing
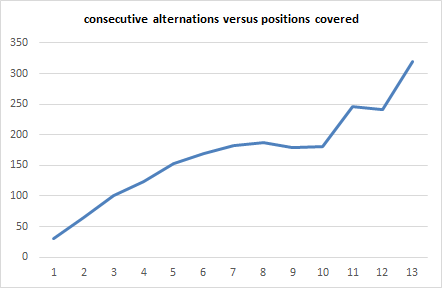
Without any further cycle start and stop work, I have been thinking about variations on the idea. Jarlve, you might like this one. I modified the spreadsheet to calculate the total count of positions covered for each cycle, then average the count of positions covered by each count of consecutive alternations. Below, x axis is CA, y axis is average positions covered, Zodiac 340.
The sheet can also show true versus false cycles if the key is known. So comparisons between statistics between true and false cycles can also be looked at in the future maybe. Transposed versus not transposed. All kinds of comparisons.
Jarlve, I’ve done symbol merges in the past but did not consider their effect on pivots. Your recent symbol merge test provoked my curiosity: If we merge certain symbols together, will more pivots appear? The answer is yes, but they may just be easy to produce this way.
Examples:
Merging 
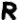
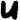

Merging 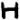
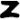
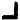


Merging 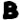
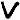
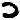


As you increase the number of merged symbols, you increase the chance of more pivots showing up. But I’m wondering if I can limit the search to the ones whose axes fall on positions divisible by 39 (or 13), and/or involve symbols that aren’t so high frequency in the ciphertext. Or maybe new pivots that correlate to increases in periodic bigrams. I’ll poke around with it some more.
I will do a little more experimenting soon. I am just wondering if false cycles and true cycles have slightly different characteristics with regards to the spacing between ciphertext. Is there a way to tell the difference?
That is the sort of question that troubles me. It may be that the difference is so small, it would be hard to detect quantitatively. These sorts of unknowns usually lead me down the path of "hey, let’s throw a machine learning classifier at it and see what it can learn, since it’s too hard for me to discover the exact relationships." For example, you could produce a big pile of homophonic test ciphers, and train the machine learning algorithm to discover the clusters of symbols that are homophones. Then see how well it would behave with test ciphers it has never seen before.
The fun part of that approach is looking into the trained algorithm to see what it might have discovered about the symbol relationships we’re looking for. You can see that in some kinds of algorithms (decision trees, genetic algorithms, etc). But they are much harder to see in neural networks, even if the predictions are accurate. If only we could devote a full time group of researchers to these kinds of things!
Does that mean the plaintext is still readable or have too many swaps occurred to preserve readability?
Not readable.
Are you shuffling the plaintext to simulate transposition?
No, just wanted to shift the focus to the encoding entirely.
I wanted to reproduce this observation. Here are my numbers, do they look the same as yours?
Yes, looks good.
Will try to reply to the other stuff later on.
Still working through my symbol merge tests, and noticed this potential 5-gram that forms at period 19 if you merge the half filled square and circle. Cipher is shown at width 19 for improved visualization of the repeats. Perhaps you’ve encountered this already.
I will do a little more experimenting soon. I am just wondering if false cycles and true cycles have slightly different characteristics with regards to the spacing between ciphertext. Is there a way to tell the difference?
One thing you can do is look at minimal hypothetical scenarios and figure it out from there.
I made a cipher with only 2 symbols, the placement of these symbols is totally random. Then encoded to 4 symbols, the encoding is totally random. Can you infer which number pairs are true cycles by looking at distances? I haven’t tried myself and will leave it up to you.
1 3 2 4 3 1 4 1 2 1 2 2 1 1 3 3 4 2 1 4 1 3 2 3 4 2 3 4 4 3 2 3 2 2 3 1 2 2 1 4 4 3 4 3 2 4 1 2 2 4 4 4 2 1 1 4 4 2 1 2 2 3 1 3 1 1 3 2 4 1 3 2 4 4 4 4 1 1 4 1 4 3 2 4 4 2 3 3 1 4 2 2 4 3 2 2 3 1 1 3 1 2 2 3 4 1 1 3 4 2 2 2 4 2 3 2 4 2 1 3 3 3 1 2 3 1 3 4 2 4 4 2 3 3 1 2 1 4 2 4 3 3 1 1 1 1 2 1 4 1 4 3 2 4 3 3 2 3 1 4 2 4 2 4 2 1 1 1 1 1 1 2 4 1 4 1 1 3 3 3 1 4 3 2 4 3 2 3 4 2 3 3 3 4 4 3 3 1 4 3
Without any further cycle start and stop work, I have been thinking about variations on the idea. Jarlve, you might like this one. I modified the spreadsheet to calculate the total count of positions covered for each cycle, then average the count of positions covered by each count of consecutive alternations. Below, x axis is CA, y axis is average positions covered, Zodiac 340.
One alternation is "AB" right. So the expected or average number of positions covered per should be about 340/63*CA. And your graph shows a drop at 10 cycle alternations. I don’t know what to think, what is your interpretation?
Jarlve, I’ve done symbol merges in the past but did not consider their effect on pivots. Your recent symbol merge test provoked my curiosity: If we merge certain symbols together, will more pivots appear? The answer is yes, but they may just be easy to produce this way.
That’s interesting. You could make a 17 by 20 heatmap (while running symbol merges) where each point is the pivot axis to find out if there are regions in which they appear more often. I recommend then to allow pivots to wrap around the cipher.
After that is done you could do the same for a 340 character part of the 408 or one of your emulation ciphers to see if there’s any major difference in counts.
I made a small bit of progress,
You will need some time to digest this, it will make your head spin.
Remember that adding an 18th column to the 340 increases untranposed period 5 bigrams to 35 from 30? It seems related to the transposed bigram bump from period 68 to 78 (especially with assumed cycle "2z"):
340: Period 5: 19, 30 ---------------------------------- Period 68: 30, 19 Period 69: 31, 21 Period 70: 31, 23 Period 71: 31, 15 Period 72: 30, 17 Period 73: 30, 21 Period 74: 29, 30 Period 75: 29, 22 Period 76: 30, 20 Period 77: 31, 18 Period 78: 31, 19
To understand it better, note that a period 4 transposition equals a period 85 untransposition, and a period 5 transposition equals a period 68 untransposition. After applying period 4 transposition to a 340 character capped version of the 408 transposed bigrams spread out from period 79 to 92:
408 (340 chars): Period 79: 31, 19 Period 80: 31, 16 Period 81: 36, 16 Period 82: 39, 19 Period 83: 43, 18 Period 84: 43, 19 Period 85: 46, 21 Period 86: 47, 20 <--- Period 87: 44, 20 Period 88: 41, 23 Period 89: 37, 17 Period 90: 32, 20 Period 91: 30, 24 Period 92: 30, 18
And after applying a period 5 transposition to the 408 transposed bigrams spread out from period 64 to 74:
408 (340 chars): Period 64: 30, 28 Period 65: 32, 19 Period 66: 39, 16 Period 67: 45, 15 Period 68: 46, 16 <--- Period 69: 43, 13 Period 70: 44, 27 Period 71: 40, 24 Period 72: 37, 18 Period 73: 34, 21 Period 74: 31, 19
It can also be done the other way around. Applying a period 68 untransposition will cause an untransposed period 5 bigram peak. And applying a period 85 untransposition causes an untransposed period 4 bigram peak. What we could do is apply a period (68+85)/2 untransposition to cause a weaker untransposed period 4 to 5 bigram peak.
It is interesting that after assuming cycle "2z" in the 340 transposed bigrams go up so sharply in the 68 to 85 range peaking at 78 which is neither period 68 or 85 but instead an intermediate. I wonder if it could be another possible indication of transposition misalignment or tranposition mismatch.
I also wonder if a period 78 untransposition would then be primary to a period 4 or 5 transposition since a period 4 or 5 transposition would not cause the peak to be directly at or around 78. 78 is very much in between of 68 and 85. 4, 5, 68 and 85 are factors of 340, it all seems vaguely connected. If period 78 untransposition is primary to period 4 or 5 tranposition then the assumed cycle "2z" observation is primary to the add 18th column observation.
Period 78 untransposition, what could it mean?
I have been under the weather and unable to keep up, so I will have to look at your posts a bit later. Sorry. But I think I will have a solution to message 1 soon.