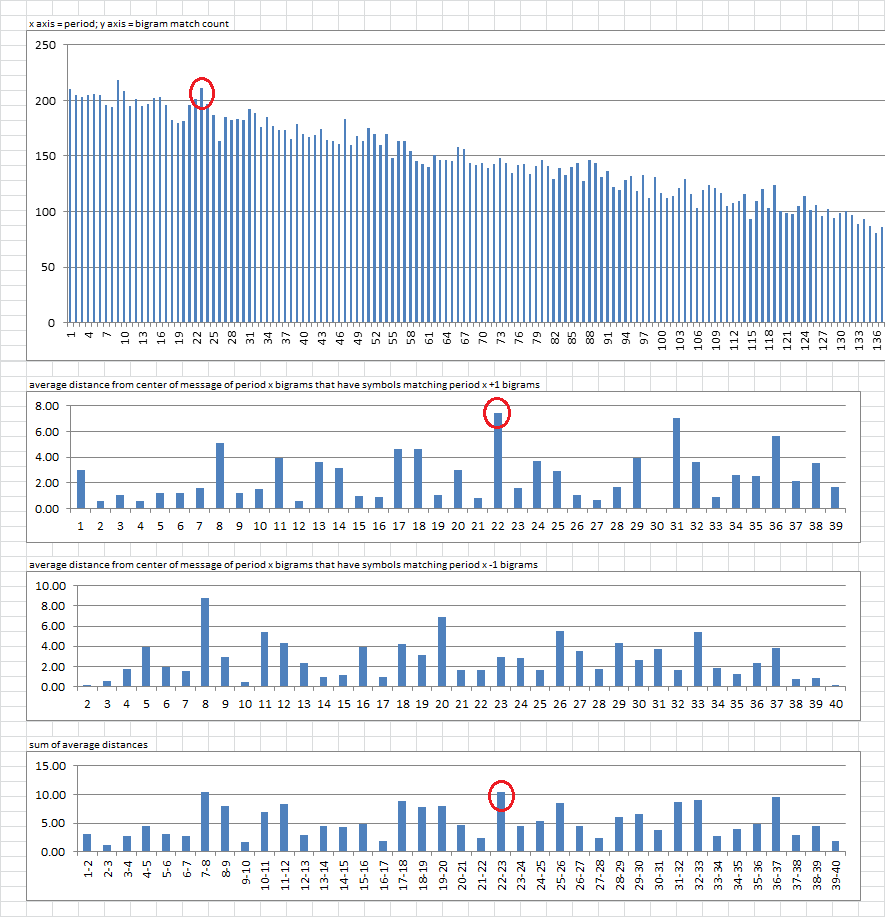
Here is your message 1. It is the one with the incomplete inscription rectangle, which is 15 x 23 and five missing plaintext in the bottom row. The mirrored message has a spike at period 11, and smaller spikes at multiples of 11. That really threw me off for a while. There is also a spike at period 9 in the LRTB transcribed version. The spike at period 23 was not predominate.

My incomplete inscription rectangle detector spreadsheet is still pretty rough, but it detected that the average position of the center of the period 22 bigrams that have symbols matching the period 23 bigrams is 7.47 positions from the center of the message. Compared to all other combinations of two adjacent periods, that was one of the largest distances, and was the clue taken with the smaller spike at period 23. I made another spreadsheet that calculates different rectangle sizes for combinations of adjacent periods, and there was one at 10 x 23 + 5 x 22.

I broke the message into two chunks, untransposed the biggest one at period 23 and tried to solve regular, mirrored, flipped and flipped and mirrored. Once I had a partial solution I untransposed the smaller chunk at period 22. Then made a worksheet with all possible combinations of putting the two untransposed rectangles together. I learned a lot working through this exercise.

Transposed message ( message 1 ):

1 2 3 4 5 6 7 2 3 8 9 10 11 11 6 12 12
8 6 5 4 7 13 9 14 2 6 15 16 9 6 6 4 8
17 6 9 5 18 4 3 8 2 12 2 2 11 4 3 17 9
2 16 19 6 4 12 5 12 2 2 7 1 2 15 18 1 20
7 2 21 22 1 4 9 11 3 7 12 8 6 3 15 7 22
19 2 2 18 2 3 1 1 21 4 14 1 14 7 6 7 1
16 3 4 6 7 18 3 15 9 8 9 9 23 7 1 8 9
3 18 10 20 6 1 18 6 1 3 1 4 1 4 6 12 11
24 18 6 6 2 3 5 17 6 2 3 16 17 9 12 7 9
6 19 1 20 14 7 6 7 8 18 8 1 17 12 20 9 8
8 12 7 4 4 8 6 3 12 7 1 3 17 13 2 14 2
10 22 12 2 7 7 12 5 8 1 7 6 14 1 22 16 11
7 4 4 17 7 9 10 15 7 9 20 16 2 2 7 10 5
20 25 17 1 9 2 12 7 1 22 11 7 1 4 6 11 3
2 16 3 16 14 3 1 7 13 3 4 18 14 22 2 3 6
16 6 2 3 6 6 6 11 3 2 13 14 22 17 6 21 8
7 11 18 12 6 5 9 20 6 9 9 18 18 8 6 8 6
5 2 12 4 22 12 18 2 7 12 8 6 18 7 6 2 1
4 14 6 9 4 3 14 9 12 8 7 14 6 3 15 6 4
20 6 16 18 18 3 1 7 3 17 7 15 18 14 7 4 2

Inscription rectangle:

2 7 22 21 3 1 22 12 1 4 15 2 18 12 7
4 8 4 6 13 17 1 3 19 1 3 2 15 2 4
7 12 12 17 7 25 14 6 6 4 18 19 2 8 5
14 9 2 22 1 20 6 8 9 1 7 22 1 3 6
18 14 5 14 3 5 7 4 7 3 6 7 7 4 8
15 3 6 13 14 10 1 4 12 1 4 15 2 18 12
7 4 8 2 16 7 8 7 9 6 3 3 2 5 12
17 9 6 3 3 2 5 12 17 18 16 6 12 9 6
3 6 8 11 16 2 12 8 16 1 1 8 5 6 11
7 14 18 6 2 16 7 8 3 6 7 12 12 17 11
1 4 18 6 3 20 7 9 2 20 6 7 4 8 10
3 1 9 6 11 9 2 20 6 10 7 3 6 4 9
18 2 9 3 6 7 12 12 17 18 14 11 19 6 8
18 6 6 2 4 15 22 17 5 3 1 9 16 6 3
16 7 20 6 1 10 10 1 3 9 14 4 2 9 2
6 18 9 16 7 9 2 8 2 8 4 1 9 16 7
20 6 5 6 11 7 14 18 6 1 21 22 17 15 6
4 8 6 3 22 17 2 8 6 7 1 21 3 6 5
6 12 12 2 1 4 13 7 18 23 1 2 4 2 4
15 7 18 22 7 4 17 6 24 9 3 7 11 14 3
3 2 11 14 12 7 3 7 11 9 2 20 2 9 2
6 18 7 18 2 11 1 14 12 8 18 1 2 13 1
14 12 8 4 9 16 7 20 6 9

EDIT: Red shows reading and transcription direction for first 17 symbols; ragged edge on right would be even if the pasted spacing was correct.

Solution:

IAMFROMLONGISLA
NDNEWYORKORIGIN
ALLYAQUEENSKIDB
UTIMOVEDTOAMORE
SUBURBANAREAAND
GREWUPONLONGISL
ANDIHADATERRIBL
YTERRIBLYSHELTE
REDCHILDHOODBEC
AUSEIHADREALLYC
ONSERVATIVEANDP
ROTECTIVEPARENT
SITREALLYSUCKED
SEEINGMYBROTHER
HAVEOPPORTUNITI
ESTHATIDIDNOTHA
VEBECAUSEOFMYGE
NDERMYIDEAOFREB
ELLIONWASGOININ
GASMANYEXTRACUR
RICULARACTIVITI
ESASICOULDSOIWO
ULDNTHAVET

I have been under the weather and unable to keep up, so I will have to look at your posts a bit later. Sorry. But I think I will have a solution to message 1 soon.

Don’t worry about it. It’s mostly a collection of loose thoughts.

Solution:

IAMFROMLONGISLA
NDNEWYORKORIGIN
ALLYAQUEENSKIDB
UTIMOVEDTOAMORE
SUBURBANAREAAND
GREWUPONLONGISL
ANDIHADATERRIBL
YTERRIBLYSHELTE
REDCHILDHOODBEC
AUSEIHADREALLYC
ONSERVATIVEANDP
ROTECTIVEPARENT
SITREALLYSUCKED
SEEINGMYBROTHER
HAVEOPPORTUNITI
ESTHATIDIDNOTHA
VEBECAUSEOFMYGE
NDERMYIDEAOFREB
ELLIONWASGOININ
GASMANYEXTRACUR
RICULARACTIVITI
ESASICOULDSOIWO
ULDNTHAVET

Well done, I’m really impressed that you solved it. It is another quote from Mia Li.

Without any further cycle start and stop work, I have been thinking about variations on the idea. Jarlve, you might like this one. I modified the spreadsheet to calculate the total count of positions covered for each cycle, then average the count of positions covered by each count of consecutive alternations. Below, x axis is CA, y axis is average positions covered, Zodiac 340.

One alternation is "AB" right. So the expected or average number of positions covered per should be about 340/63*CA. And your graph shows a drop at 10 cycle alternations. I don’t know what to think, what is your interpretation?

There are not very many 10 CA cycles, and the average is therefore skewed. I should probably take a closer look when I get back to work. I made a suite that creates period 20 transposed messages from your 100 message library, perfect cycles, and a semi inefficient key. Then looks at all cycles, true or false 1 CA and above. The averages the count of positions covered for each CA and uses the graph. There is always an almost perfect diagonal line until you get to higher CA because the count of higher CA is smaller. The line get bumpier because there are not enough cycles to make a smooth average.

I also wanted to note that regardless of whether the cycles in the message are analyzed with the message right side up or rotated 180 degrees, the top rows have higher totals than the bottom rows. I could not determine encoding direction.

Also, with regards to positions 166-171 having very high disruptor counts in the 340, I can tell you that after making about 30 messages, there were other positions with high disruptor counts, but not all in a row like that. But I am not saying that it means anything.

I plan on continuing work in this area.

Here are the spikes that helped me solve message 1.

Here are the spikes that helped me solve message 1.

How does "average distance from center of message of period x bigrams that have symbols matching period x+1 bigrams" work? It basicly tries to detect mixing of periods right?

I found an easy way to solve that cipher (I am from long island…). Reverse it (or what you call rotate 180 degrees) and then transpose period 15. You may have a blind spot in your periodical analysis. When a cipher is transposed with a period 15 untransposition then it will peak at transposed period 15 with a weaker peak at untransposed period 23:

(transposed, untransposed)

Period 15: 163, 134 <--- (peak)
Period 16: 135, 134
Period 17: 126, 130
Period 18: 127, 124
Period 19: 122, 128
Period 20: 130, 126
Period 21: 133, 133
Period 22: 133, 138
Period 23: 133, 149 <--- (weaker peak)


340 transposition matrix:

1   2   3   4   5   6   7   8   9   10  11  12  13  14  15  16  17
18  19  20  21  22  23  24  25  26  27  28  29  30  31  32  33  34
35  36  37  38  39  40  41  42  43  44  45  46  47  48  49  50  51
52  53  54  55  56  57  58  59  60  61  62  63  64  65  66  67  68
69  70  71  72  73  74  75  76  77  78  79  80  81  82  83  84  85
86  87  88  89  90  91  92  93  94  95  96  97  98  99  100 101 102
103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119
120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136
137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153
154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170
171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187
188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204
205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221
222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238
239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255
256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272
273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289
290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306
307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323
324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340


period 15 transposed:

1   24  47  70  93  116 139 162 185 208 231 253 275 297 319 2   25
48  71  94  117 140 163 186 209 232 254 276 298 320 3   26  49  72
95  118 141 164 187 210 233 255 277 299 321 4   27  50  73  96  119
142 165 188 211 234 256 278 300 322 5   28  51  74  97  120 143 166
189 212 235 257 279 301 323 6   29  52  75  98  121 144 167 190 213
236 258 280 302 324 7   30  53  76  99  122 145 168 191 214 237 259
281 303 325 8   31  54  77  100 123 146 169 192 215 238 260 282 304
326 9   32  55  78  101 124 147 170 193 216 239 261 283 305 327 10
33  56  79  102 125 148 171 194 217 240 262 284 306 328 11  34  57
80  103 126 149 172 195 218 241 263 285 307 329 12  35  58  81  104
127 150 173 196 219 242 264 286 308 330 13  36  59  82  105 128 151
174 197 220 243 265 287 309 331 14  37  60  83  106 129 152 175 198
221 244 266 288 310 332 15  38  61  84  107 130 153 176 199 222 245
267 289 311 333 16  39  62  85  108 131 154 177 200 223 246 268 290
312 334 17  40  63  86  109 132 155 178 201 224 247 269 291 313 335
18  41  64  87  110 133 156 179 202 225 248 270 292 314 336 19  42
65  88  111 134 157 180 203 226 249 271 293 315 337 20  43  66  89
112 135 158 181 204 227 250 272 294 316 338 21  44  67  90  113 136
159 182 205 228 251 273 295 317 339 22  45  68  91  114 137 160 183
206 229 252 274 296 318 340 23  46  69  92  115 138 161 184 207 230


period 15 untransposed:

1   16  31  46  61  76  91  106 121 136 151 166 181 196 211 226 241
256 271 286 301 316 331 2   17  32  47  62  77  92  107 122 137 152
167 182 197 212 227 242 257 272 287 302 317 332 3   18  33  48  63
78  93  108 123 138 153 168 183 198 213 228 243 258 273 288 303 318
333 4   19  34  49  64  79  94  109 124 139 154 169 184 199 214 229
244 259 274 289 304 319 334 5   20  35  50  65  80  95  110 125 140
155 170 185 200 215 230 245 260 275 290 305 320 335 6   21  36  51
66  81  96  111 126 141 156 171 186 201 216 231 246 261 276 291 306
321 336 7   22  37  52  67  82  97  112 127 142 157 172 187 202 217
232 247 262 277 292 307 322 337 8   23  38  53  68  83  98  113 128
143 158 173 188 203 218 233 248 263 278 293 308 323 338 9   24  39
54  69  84  99  114 129 144 159 174 189 204 219 234 249 264 279 294
309 324 339 10  25  40  55  70  85  100 115 130 145 160 175 190 205
220 235 250 265 280 295 310 325 340 11  26  41  56  71  86  101 116
131 146 161 176 191 206 221 236 251 266 281 296 311 326 12  27  42
57  72  87  102 117 132 147 162 177 192 207 222 237 252 267 282 297
312 327 13  28  43  58  73  88  103 118 133 148 163 178 193 208 223
238 253 268 283 298 313 328 14  29  44  59  74  89  104 119 134 149
164 179 194 209 224 239 254 269 284 299 314 329 15  30  45  60  75
90  105 120 135 150 165 180 195 210 225 240 255 270 285 300 315 330

How does "average distance from center of message of period x bigrams that have symbols matching period x+1 bigrams" work? It basicly tries to detect mixing of periods right?

Yes. I calculated the center position of each period x bigram where the symbols match bigrams of period x+1. And the center position of each period x+1 bigram where the symbols match bigrams of period x. If the average center position is far from 170.5, then that could be a clue to an incomplete inscription rectangle.

*******

Here is an idea, maybe you have done it. Slide through the message, designating chunks of positions that are multipliers of 19. Untranspose, mirror, flip and flip and mirror. Try to solve. If no solution, then slide one more position. Repeat.

For example, start at position 1 and designate 19 x 8 = 152 positions all the way to position 152. Then untranspose and try to solve that chunk. Then slide the chunk to positions 2 to 153. Repeat until at end of message. Then use a chunk size 19 x 9, 19 x 10, etc.

Or you could use multiples of 15 or 29 with the mirrored 340. Etc. With different sized chunks, there will be different scores.

So all of the scores for chunk sizes of 152 would have to be compared with each other, all of the scores for chunk sizes of 19 x 9 = 171 would have to be compared with each other, etc.

An untransposed and flipped of the same position span and chunk size with scores higher than the mirrored and flipped and mirrored would be a good clue. Or if the mirrored and flipped and mirrored have scores that are higher than the untransposed and flipped, then that would also be a good clue.

*******

That’s interesting. You could make a 17 by 20 heatmap (while running symbol merges) where each point is the pivot axis to find out if there are regions in which they appear more often. I recommend then to allow pivots to wrap around the cipher.

I tried to go down this path but found that it’s easy to overcount pivots when they appear due to merges. This is because a partial pivot will turn into a full pivot for an exact minimum number of symbols. I will try to briefly explain with some examples. Note that I’m only considering pivots that are in the same orientation as the existing ones.

No 2-symbol merges produce new pivots.

There is only one way that a pivot forms via a 3-symbol merge. It is at this partial pivot:

The two + symbols are in the right place. And U appears in both parts of the partial pivot. So to form full pivot, only J, R and U need to be merged. Thus, any n-symbol merge (where n>3) that includes some symbols in addition to J, R and U would be overcounted.

As we get into 4-symbol merges, all we need is to find partial pivots where one symbol is in the right place. Then we just merge the four remaining symbols. Here’s an example partial pivot:

Note the B symbols are in the right place. So we only need to merge the other four symbols together.

Another example:

Note the half filled circles are in the right place. So we just need to merge the other four symbols.

Here is the cipher with axes highlighted for all “partial pivots” where one symbol is in the right place in both segments of the pivot, requiring merging of four symbols to complete the pivot:

At each symbol, you can look in the north and west directions to find the common symbol.

If we allow merging 5 symbols, then we only need to find a single symbol shared by both parts of the partial pivot. They do not have to be in the correct positions. Thus merging 5 or more symbols forces arbitrary pivots to appear.

So, I’m not sure how much value there is in counting pivots that form after merges. It may be more useful to count the "partial pivot" patterns that already exist in the unmerged ciphertext. We can compare that to reference counts for shuffles and other ciphers.

This exercise made me wonder: Would it be worthwhile to look for "anagram pivots" (pivots where the symbols in the two parts are the same but appear in any order)? (My hunch is "no", but it’d be a fun experiment).

Anyway, I think I’m going to move away from this and look at the effects of symbol merges on periodic ngram repeats.

Anyway, I think I’m going to move away from this and look at the effects of symbol merges on periodic ngram repeats.

I would love to see a study on that.

I’ve only merged "2z" and haven’t looked any further. The transposed period 78 bigram peak that occurs with it certainly has my interest at the moment. I came up with an idea that could explain it: grid-based angles. A 45 degree angle is perfectly diagonal. A period 45 untransposition looks like this:

1   46  91  136 181 226 271 316 2   47  92  137 182 227 272 317 3
48  93  138 183 228 273 318 4   49  94  139 184 229 274 319 5   50
95  140 185 230 275 320 6   51  96  141 186 231 276 321 7   52  97
142 187 232 277 322 8   53  98  143 188 233 278 323 9   54  99  144
189 234 279 324 10  55  100 145 190 235 280 325 11  56  101 146 191
236 281 326 12  57  102 147 192 237 282 327 13  58  103 148 193 238
283 328 14  59  104 149 194 239 284 329 15  60  105 150 195 240 285
330 16  61  106 151 196 241 286 331 17  62  107 152 197 242 287 332
18  63  108 153 198 243 288 333 19  64  109 154 199 244 289 334 20
65  110 155 200 245 290 335 21  66  111 156 201 246 291 336 22  67
112 157 202 247 292 337 23  68  113 158 203 248 293 338 24  69  114
159 204 249 294 339 25  70  115 160 205 250 295 340 26  71  116 161
206 251 296 27  72  117 162 207 252 297 28  73  118 163 208 253 298
29  74  119 164 209 254 299 30  75  120 165 210 255 300 31  76  121
166 211 256 301 32  77  122 167 212 257 302 33  78  123 168 213 258
303 34  79  124 169 214 259 304 35  80  125 170 215 260 305 36  81
126 171 216 261 306 37  82  127 172 217 262 307 38  83  128 173 218
263 308 39  84  129 174 219 264 309 40  85  130 175 220 265 310 41
86  131 176 221 266 311 42  87  132 177 222 267 312 43  88  133 178
223 268 313 44  89  134 179 224 269 314 45  90  135 180 225 270 315

In between of that we have angle 67.5 "(45+90)/2", a period 68 untransposition is equal to a period 5 transposition. Then in between of that we have angle 78.75 "(67.5+90)/2", so I think that 78 may be just that. To further illustrate grid-based angles:

grid-based angles:

45 degrees: (diagonal)
1
 2
  3
   4
    5

67.5 degrees: (notice possible period 15/19 correlation)
12
  34
    56
      78
        90

78.75 degrees:
1234
    5678
        9012
            3456
                7890

So now I’d like to explore if he encoded or transposed in that way.

BAT IF PRIOPRATPWC WITH YAGYEJLXNQHNVXSDGESUISVAULEQAPIOHEDENEUABWCRCJF HAS DIEPO SERVE USHANM BOAR ATIESUSGIANYDaIREGEDONHELI LAWS WICH AT GROG ME QIFATTRINKWEJ

Y WORKING BACK OF PRODUCED BY "THEY WOULD HAVE NUMBERS OF THE FIRST AND THE PUBLIC ALLOWING THE CALL" Y MAKING WITHING THE COMPANDING FROM THEREVER SANDING THE PUBLICATIONS OF THE COULD JUSTHAT WAS R EVER

Quick question for you all. The first one is a chunk size bite of the 340 8 columns in a spiral route which incorporates the first pivot nicely. nothing at all in that one.
the second one is exactly the same but I added the seven pivot characters at the end again. Why do I get such a vast difference in readability? it also gives me other variations of this at different AZ points.

Hey Mr lowe,

I’m not sure. Your first plaintext string scores 20k and your second plaintext string scores 30k+. Could you report the multiplicity of both cipher strings? You can find the stat with AZdecrypt under Stats -> Unigrams. Most readable plaintext score around 24k, since your second plaintext string scores over 30k its multiplicity may be very high which allows AZdecrypt to come up with very high scoring solutions which are not real solves.

AZdecrypt unigram stats for:
————————————————–
Length: 167
Symbols: 160
Dimensions: 17 by 10
Multiplicity: 0.9580838323353293
Entropy: 7.299871957144694
Index of coincidence:
– Raw: 14
– Normalized: 0.000505014068249044
Flatness: 0.5218749999999994
Unigram repeats per 17 characters: 0

hey jarlvie.. it must be the repeats of the pivots.

AZdecrypt unigram stats for:
————————————————–
Length: 167
Symbols: 160
Dimensions: 17 by 10
Multiplicity: 0.9580838323353293
Entropy: 7.299871957144694
Index of coincidence:
– Raw: 14
– Normalized: 0.000505014068249044
Flatness: 0.5218749999999994
Unigram repeats per 17 characters: 0

hey jarlvie.. it must be the repeats of the pivots.

For your cipher, 160 out of 167 symbols are unique so practically anything could be made fit. While using 5-grams I would not attempt multiplicities higher than 0.35, your string is 0.95! The very best AZdecrypt has cracked was a 6 line 408 with a multiplicity of 0.5 while using 7-grams.

Here are the first results of my tests of the effects of symbol merges on periodic ngrams. The motivation is: If there is a homophonic aspect to the cipher text, and the spikes in periodic ngrams are real indications of some transposition occurring in addition to substitution, then will we see higher ngram counts at interesting periods when we merge the correct symbols together?

I considered all possible combinations of pairs of symbols. For each pair of symbols:

1) Merge them in the Z340 cipher text (that is, replace all occurrences of the 2nd symbol with the 1st symbol)
2) Count the repeating ngrams in all periods from 1 to 170
3) Compare to repeating ngrams in all periods of the unmodified Z340. For example, if period 10 jumps from 20 bigrams to 25 bigrams when a symbol pair is merged, then the value I track is 25-20 = 5.

This generated a large amount of data so I made an interactive charting tool to help navigate it all:

http://zodiackillerciphers.com/symbol-merge-ngrams/

Screenshot:

Click the image or link above to open the charting tool. The x-axis is the period, and the y-axis is the gain in repeating bigrams after merging the shown symbols. You can hover your mouse over the chart to see data values. Here is an explanation for the controls:

– Next: Show the chart for the next symbol pair
– Skip 20: Jump past the next 20 symbol pairs
– Last: Jump to the chart for the last symbol pair

– Prev: Show the chart for the previous symbol pair
– Skip 20: Jump past the previous 20 symbol pairs
– First: Jump to the chart for the first symbol pair

– Sort by: Here you can change how the charts are sorted:

1) Sum of increases in ngram repeats: This is the sum of ngram gains for all periods. Charts with the highest sums are shown first.
2) Max increase: Charts with highest gains in ngrams are shown first
3) Sigma: To compute sigma, we first compute mean and max gain for all periods, and standard deviation. Sigma is (max-mean) divided by standard deviation.
4) Period of max increase: Charts are arranged in order of which periods had the maximum gain in ngrams.
5) Period P spikes first (P can be from 1 to 170): Charts with max gain occuring at period P are shown first
6) Show data for: Here you can show charts for periodic 2-grams, 3-grams or 4-grams.

Let me know if there are any problems with the tool.

I find that it is very hard to judge the significance of the results, so I’m running a shuffle experiment and will update with those results soon. An early and interesting result is that merging produces two 4-grams repeats at period 19 (because the merge produces one 5-gram repeat at period 19).

The shuffle experiment considers that to be significant since only 4% of shuffles for those merged symbols produced peaks of 1, and 96% of them were 0.

Nice stuff doranchak! Very well built tool.

A few issues for me,

Skipping backwards skips 10 instead of 20.

1) Sum of increases in ngram repeats: This is the sum of ngram gains for all periods. Charts with the highest sums are shown first.
2) Max increase: Charts with highest gains in ngrams are shown first

This seems to produce exactly the same results. Also, select 4-grams and then switching between the two sorting options a couple of times produces strange results.

3) Sigma: To compute sigma, we first compute mean and max gain for all periods, and standard deviation. Sigma is (max-mean) divided by standard deviation.
4) Period of max increase: Charts are arranged in order of which periods had the maximum gain in ngrams.

I don’t understand how these are sorted. Why does 1 of 1953 has a higher sigma then 2 of 1953? Many of the pages after 1 have much higher maximum increases.

Only untransposed/untransformed periods are included. Is it possible to find the maximum increase for a period? Would it be possible to weigh increases in repeats in another way that includes the signifance of the from-to range? For instance merging "+B" shows the highest increase with +16 at period 114. But when looking at the original 340, this period has only 15 repeats. So it goes up from 15 to 31, that may be special in its own way but I wonder if for instance going from 30 to 38 would be more statistically significant in terms of rating the period as interesting considering transposition etc.

I also find the results are difficult to interpret. What ASCII symbols are these that create a 5-gram repeat?