I am a little bit excited about a new discovery. A short background before I get to the point. I made two new spreadsheets this week. One is where I can paste messages of different sizes and shapes, but not necessarily complete rectangles, into the sheet and calculate the bigram repeats for all periods. I want to be able to use this as a way to check various untranspositions and different areas of messages to look for multiple transcription rectangles, etc. etc.
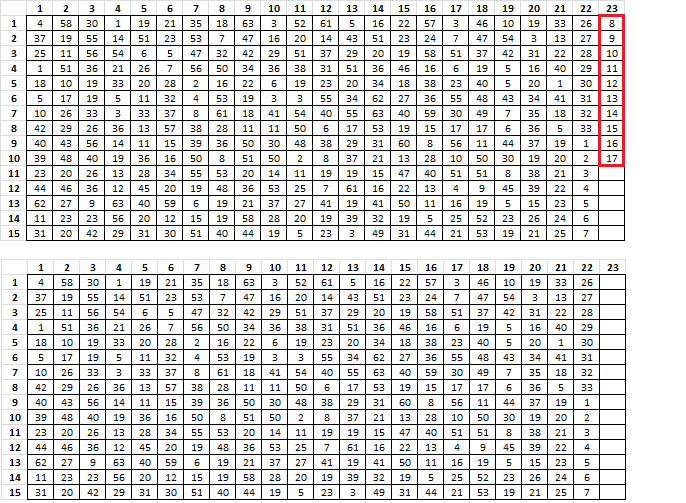
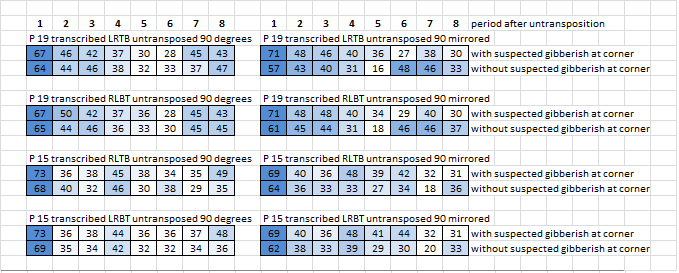
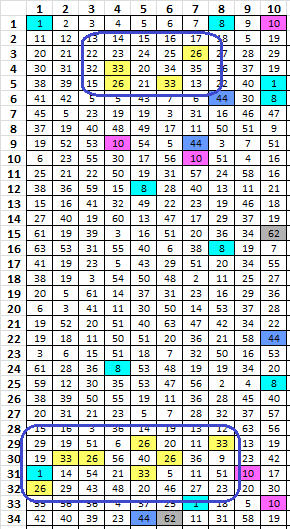
I started using the spreadsheet to look at the four corners of the 340. Maybe the inscription rectangle was complete, and therefore one of the four corners or top or bottom row is gibberish. For each of four horizontal transcription directions coming from each corner, I untransposed by drafting into either 15 or 19 columns, rotating 90 degrees, and then flipping. I calculated the repeats, then deleted the chunk of message at the end and calculated the repeats again. If the chunk of message at the end is gibberish, then the count of period 1 repeats should go up. Then I mirrored the message and did the same thing. Example:
In no case did the count of period 1 repeats go up when I deleted the suspected gibberish corner. In every case the count went down. Maybe this is a good way to infer transcription direction. In all but one case the period 2 repeat count dropped. This implies that all four corners are part of the matrix.
O.k. so maybe it is an incomplete inscription rectangle with 340 plaintext, or maybe fewer and some gibberish somewhere. Or maybe it is a complete inscription rectangle but the gibberish is elsewhere. We have discussed this for quite a long time. Could be a row, column, or partial of either. Could be random.
I decided to look for random, and guessed that if I was Zodiac and I wanted to fill a 17 x 20 rectangle, but had a message that was either 323 or 330, one way to do it would be to make sure to insert 17 or 10 nulls as I transcribed, or maybe before I transcribed, counting as I went. Two ways to do this. Use a variety of different symbols, or use one or maybe two or three different symbols so that I can keep count of my nulls. The Army Manual discusses using nulls in a similar way.
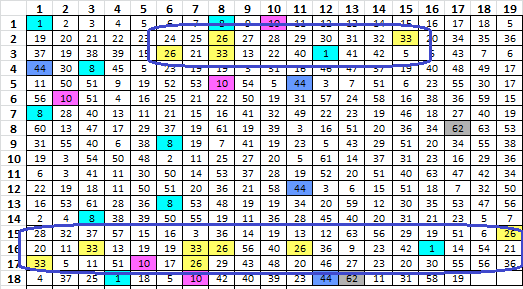
I remember vaguely that we talked about maybe one particular symbol used as null, like the +. And we deleted the + and got no results. I cannot remember how extensively we went into this idea. My second spreadsheet this week removes all of each symbol 1 to 63, and calculates the suspected period repeat count. It can also remove two symbols. Anyway, here are the results:
There are two symbols, when deleted individually, that result in a slight increase in period 19 bigram repeats. Symbol 1 and symbol 33.
Period 19 repeats before removing all of any symbol: 67
Left column symbol removed, right column count of period 19 repeats
1 69
2 58
3 42
4 60
5 47
6 55
7 51
8 58
9 66
10 59
11 40
12 52
13 51
14 48
15 46
16 30
17 52
18 43
19 28
20 50
21 50
22 51
23 41
24 60
25 51
26 60
27 50
28 46
29 39
30 49
31 49
32 54
33 69
34 52
35 63
36 43
37 42
38 53
39 51
40 47
41 52
42 63
43 64
44 64
45 60
46 53
47 49
48 52
49 51
50 44
51 45
52 59
53 54
54 67
55 62
56 66
57 53
58 61
59 54
60 56
61 55
62 62
63 62
That is interesting. So what about combinations of two symbols? There are 1,953 combinations. So I checked them all. Of the 1,953 combinations there were only 7 that resulted in a slight increase in period 19 repeats when those two symbols were removed.
1 and 10
1 and 33
1 and 44
1 and 62
33 and 8
33 and 26
33 and 44
Not only do period 19 repeats go up when I remove symbols 1 and 33 individually, but it also goes up when I delete both of them together. And, of the 7 of 1,953 combinations of two symbols when removed, all of them include symbol 1 or symbol 33. Symbol 44, when removed with symbol 1 or 33 also results in an increase.
But that isn’t even the most interesting part. After I got home last night I took another look at symbols 1 and 33. Guess what? They are two of the three box corner symbols!
Are the box corners nulls? Did Zodiac put nulls into the message in shapes or patterns that we could find, such as box corners, pivots, etc, or parts of these shapes or patterns? What are the odds of two symbols appearing in symmetrically positioned boxes, and those two symbols, individually and together, when removed, result in an increase in period 19 repeats?
Hey smokie,
Interesting finds. There are quite a few things that increase bigrams. Offsetting the column order by +1 gives 45 period 19 bigram repeats, but no subsequent period 38 bigram repeats. Perhaps try to find alterations that increase period n and n*2 repeats. I have stopped my cipher work for the moment but will be around to throw a comment now and then.
Hey smokie,
Interesting finds. There are quite a few things that increase bigrams. Offsetting the column order by +1 gives 45 period 19 bigram repeats, but no subsequent period 38 bigram repeats. Perhaps try to find alterations that increase period n and n*2 repeats. I have stopped my cipher work for the moment but will be around to throw a comment now and then.
I worked on period 38 at lunch today, and there are several symbols, when removed, increase period 38 repeats, and dozens of two symbol combinations, when removed, increase period 38 repeats. Since the count of period 38 repeats is so low, it seems that is not difficult to do.
What perplexes me for the moment is why all 7 combinations of two symbols that increase period 19 repeats include either symbol 1 or symbol 33. Removing any of the other symbols individually in those combinations lowers the count, but when removing symbol 1 or 33, counter balances the reduction.
I plan on exploring this concept more thoroughly, my next little project. It is fine that you want to stop for a while. We have plenty of time and taking time off is good for thinking of new ideas.
I like this. My new hypothesis is that Zodiac planted symbols throughout the message before or during transcribing, in patterns. They are nulls, but do not affect the period 15 / 19 repeats too much. Removing combinations of some of them will correct misalignments in an untransposed message.
If you compare the 340 and the mirrored 340 and keep the symbols that are the same you get the following (top code box). The "F" symbol lines up diagonally with the "-" symbol. Most likely nothing but perhaps someone can work with it.
mirrored: P D G V | F * F U + 2 - + - D 5 | 4 C O < P B z
Will continue at comfortable pace…
Okay smokie,
My guess is that, if the 340 has period 2 bigrams just like the 408 (which is not an unreasonable assumption) then fixing the misalignment will restore these counts. Take for example the 408 (340 chars) with a period 19 transposition, it has 46 bigrams at period 19 and 38 bigrams at period 38. Then, after removing one symbol in the middle of the cipher there are 40 bigrams at period 19 and only 22 bigrams at period 38.
1 15 19 1 5 1 44 13 26 34 46 4 45 38 33 30 15 2 15 2 16 29 41 28 24 9 26 25 40 38 23 24 5 9 27 12 9 5 3 17 6 7 47 30 50 45 50 17 44 13 22 40 3 34 17 32 17 4 18 30 3 48 38 26 22 37 45 29 28 11 3 29 8 13 37 18 5 19 8 9 49 21 18 27 46 6 10 35 18 51 11 38 26 10 19 4 20 31 10 12 26 7 6 27 22 21 42 48 6 39 39 14 6 24 6 21 26 42 20 13 32 29 48 8 22 3 30 12 48 52 26 52 45 7 1 32 6 22 50 35 10 1 20 30 37 25 8 44 45 54 16 54 2 22 33 2 15 37 39 10 41 5 1 27 28 42 43 4 20 54 32 8 3 34 43 14 51 41 7 52 36 50 8 1 6 1 41 47 19 9 23 35 10 17 39 7 52 3 12 10 10 37 41 17 2 50 19 42 10 24 19 44 50 40 46 5 36 9 54 6 1 7 21 2 52 26 1 11 25 36 26 19 10 47 24 10 15 32 33 50 15 31 5 16 54 2 12 26 37 45 23 34 4 26 16 14 19 2 46 14 36 43 23 29 41 13 19 38 8 16 33 3 12 53 30 48 46 27 49 51 42 1 39 46 11 17 39 29 26 30 41 30 11 37 49 38 44 16 18 3 42 26 33 7 27 40 46 18 19 7 38 21 16 47 34 34 15 2 41 1 14 54 14 28 4 27 36 45 23 14 49 33 17 15 42 32 2 7 7
Okay smokie,
My guess is that, if the 340 has period 2 bigrams just like the 408 (which is not an unreasonable assumption) then fixing the misalignment will restore these counts. Take for example the 408 (340 chars) with a period 19 transposition, it has 46 bigrams at period 19 and 38 bigrams at period 38. Then, after removing one symbol in the middle of the cipher there are 40 bigrams at period 19 and only 22 bigrams at period 38.
1 15 19 1 5 1 44 13 26 34 46 4 45 38 33 30 15 2 15 2 16 29 41 28 24 9 26 25 40 38 23 24 5 9 27 12 9 5 3 17 6 7 47 30 50 45 50 17 44 13 22 40 3 34 17 32 17 4 18 30 3 48 38 26 22 37 45 29 28 11 3 29 8 13 37 18 5 19 8 9 49 21 18 27 46 6 10 35 18 51 11 38 26 10 19 4 20 31 10 12 26 7 6 27 22 21 42 48 6 39 39 14 6 24 6 21 26 42 20 13 32 29 48 8 22 3 30 12 48 52 26 52 45 7 1 32 6 22 50 35 10 1 20 30 37 25 8 44 45 54 16 54 2 22 33 2 15 37 39 10 41 5 1 27 28 42 43 4 20 54 32 8 3 34 43 14 51 41 7 52 36 50 8 1 6 1 41 47 19 9 23 35 10 17 39 7 52 3 12 10 10 37 41 17 2 50 19 42 10 24 19 44 50 40 46 5 36 9 54 6 1 7 21 2 52 26 1 11 25 36 26 19 10 47 24 10 15 32 33 50 15 31 5 16 54 2 12 26 37 45 23 34 4 26 16 14 19 2 46 14 36 43 23 29 41 13 19 38 8 16 33 3 12 53 30 48 46 27 49 51 42 1 39 46 11 17 39 29 26 30 41 30 11 37 49 38 44 16 18 3 42 26 33 7 27 40 46 18 19 7 38 21 16 47 34 34 15 2 41 1 14 54 14 28 4 27 36 45 23 14 49 33 17 15 42 32 2 7 7
Yeah, removing only one symbol can make a big difference. Here, left column is the symbol, right column is the period 38 bigram count after removing all of that symbol and shifting all other symbols accordingly. Period 38 bigrams, the way I count = 44. There are several which increase this count, including symbol 4, one of the box corner symbols.
1 44
2 38
3 41
4 46
5 28
6 35
7 44
8 34
9 40
10 30
11 30
12 32
13 37
14 39
15 37
16 44
17 29
18 41
19 21
20 37
21 46
22 30
23 43
24 39
25 40
26 43
27 33
28 29
29 38
30 37
31 28
32 39
33 41
34 42
35 37
36 41
37 46
38 42
39 46
40 32
41 40
42 46
43 51
44 40
45 36
46 38
47 49
48 40
49 34
50 35
51 32
52 34
53 35
54 37
55 30
56 38
57 36
58 38
59 34
60 42
61 47
62 41
63 42
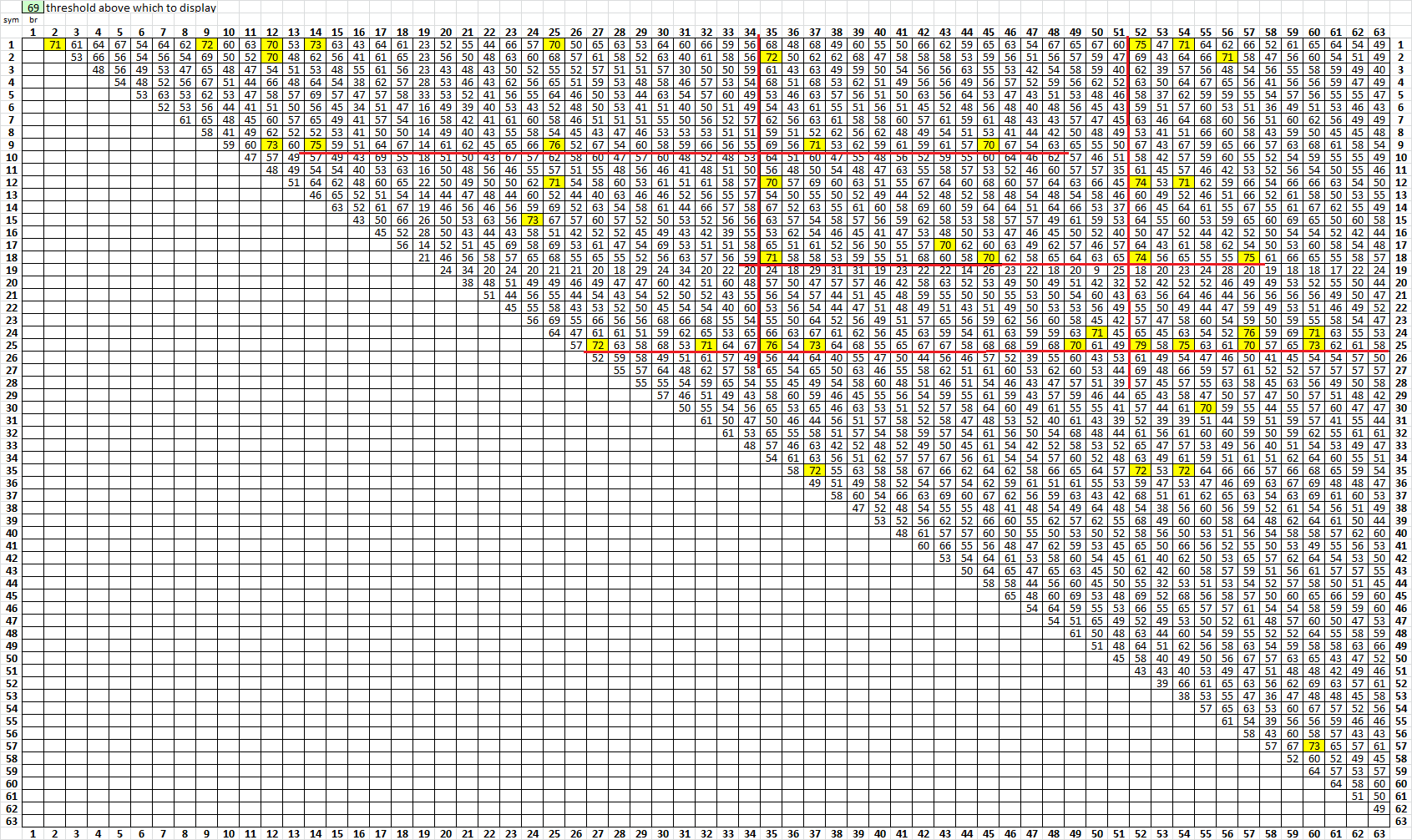
Here is period 15, my base count 69. Several symbols, when removed, increase period 15 repeats: 9, 12, 14, 18, 25, 35, 37, 52 and 54. Look at the table below, and you will see that a lot of these symbols, when removed in combination with other symbols, increase repeats. I wonder why. I wonder if this is just nonsense. Or perhaps this examination can be used to determine transcription direction. I will have to make some test messages with two symbols as nulls and see what happens. Maybe count of the removed symbol makes a difference. And also whether the symbol removed is a member of a repeat set.
1 68
2 65
3 59
4 61
5 59
6 54
7 63
8 56
9 71
10 62
11 59
12 71
13 56
14 70
15 65
16 52
17 63
18 71
19 18
20 54
21 56
22 50
23 61
24 64
25 74
26 55
27 65
28 58
29 58
30 62
31 55
32 66
33 57
34 62
35 71
36 61
37 72
38 53
39 63
40 62
41 57
42 66
43 64
44 59
45 66
46 66
47 52
48 66
49 68
50 62
51 50
52 72
53 48
54 70
55 59
56 61
57 66
58 53
59 63
60 68
61 64
62 56
63 56
Period 15 two symbol combinations removed. As with period 19, some symbols seem, even in combination with other symbols, increase repeat count.
So what about combinations of two symbols? There are 1,953 combinations. So I checked them all. Of the 1,953 combinations there were only 7 that resulted in a slight increase in period 19 repeats when those two symbols were removed.
1 and 10
1 and 33
1 and 44
1 and 62
33 and 8
33 and 26
33 and 44Not only do period 19 repeats go up when I remove symbols 1 and 33 individually, but it also goes up when I delete both of them together. And, of the 7 of 1,953 combinations of two symbols when removed, all of them include symbol 1 or symbol 33. Symbol 44, when removed with symbol 1 or 33 also results in an increase.
I just checked the cycle relationships between all of the above symbols. There is no cycle relationship of any significance. You could make a transposition message, include two nulls and cycle them with each other. The message would be very difficult to solve unless you knew what he did. But this is not it.
1 and 10
1 and 33
1 and 44
1 and 62
33 and 8
33 and 26
33 and 44
Some of these symbols seem to be biased to the top and bottom of the message. Very few of the symbols are near the middle of the message. Symbols 26 and 33 are clustered together. Drafted into 10 columns, and then 19 columns.
EDIT: I drafted the message into 5 to 68 columns, and didn’t see any patterns that struck me as being particularly interesting, except for the box corners at 17 columns.
I am going to make 6 test messages.
Smokie55ABC have 17 x 20 inscription rectangles LRTB, reading the symbols off vertically TBLR, and transcribing into a 17 x 20 transcription rectangle. One polyphone and cycles about the same as the 340. There are no nulls, so I want to see what happens with the "symbol as null" detector spreadsheet suite.
Smokie55A ( 59 symbols )
1 2 3 4 5 6 7 8 9 10 7 11 12 8 13 14 15
16 17 18 7 19 20 21 22 23 24 25 26 27 8 7 28 11
17 29 30 31 32 22 33 1 34 35 36 37 38 39 17 17 40
39 24 41 16 2 42 26 2 18 43 4 44 9 45 46 12 17
13 22 15 27 19 47 31 7 48 23 26 35 40 21 14 3 7
49 50 51 32 45 30 36 27 14 29 17 20 49 26 25 36 52
27 17 49 24 28 15 17 33 42 13 14 32 2 39 52 8 11
35 37 12 18 25 20 13 28 16 40 17 48 3 20 36 7 27
12 33 47 36 42 17 24 5 21 4 53 19 14 16 9 17 54
37 15 17 55 28 37 56 35 13 46 33 28 10 7 1 40 19
38 50 41 35 32 31 34 54 44 26 18 49 12 12 52 23 39
22 36 7 51 44 2 20 5 8 28 17 21 13 39 17 32 47
17 1 18 20 28 2 27 42 11 30 10 17 37 16 18 57 5
21 18 39 30 37 43 21 7 13 2 17 17 1 4 25 52 15
3 14 56 20 55 23 11 13 26 46 36 2 41 31 30 38 40
57 5 49 30 40 17 54 31 16 48 46 9 17 16 22 43 7
35 17 10 55 21 17 52 24 47 2 34 4 11 18 25 58 42
3 25 48 54 56 24 20 45 26 17 39 30 22 15 37 12 52
17 18 33 5 31 11 17 38 13 40 27 57 59 14 45 26 6
6 9 28 50 10 47 25 17 39 34 24 23 53 36 39 20 4
There are 65 period 20 bigram repeats. Checking for symbols, when removed, increase bigram repeats, symbol 6 does that and increases repeats to 67.
1 56
2 44
3 48
4 44
5 44
6 67
7 37
8 44
9 41
10 53
11 42
12 38
13 38
14 44
15 37
16 36
17 22
18 41
19 42
20 34
21 44
22 44
23 57
24 39
25 53
26 39
27 38
28 29
29 59
30 49
31 50
32 51
33 45
34 56
35 32
36 41
37 44
38 59
39 37
40 47
41 55
42 38
43 52
44 51
45 43
46 46
47 51
48 46
49 47
50 57
51 61
52 49
53 55
54 41
55 56
56 54
57 60
58 61
However, when checking for two symbol combinations, only one combination tests positive. Symbols 38 and 50. Smokie55A does not behave as the 340.
Smokie55B has 56 symbols and base count of period 20 repeats is 70.
1 2 3 4 5 6 7 8 9 10 11 12 2 13 14 15 16
2 17 18 16 19 20 2 21 3 1 22 23 24 25 20 26 23
12 27 28 29 2 30 7 31 2 32 5 33 31 23 34 35 12
36 37 38 39 22 2 18 40 3 25 27 34 37 11 14 12 18
8 41 42 26 33 2 43 44 25 45 14 31 2 45 1 46 18
44 7 37 21 47 4 13 35 29 40 48 26 49 18 27 3 3
23 14 32 50 20 23 22 31 2 33 40 31 27 21 47 23 5
8 7 25 29 35 51 1 36 18 16 52 22 50 17 27 45 24
50 1 2 11 31 44 44 7 15 47 37 13 37 14 2 43 6
21 51 30 35 45 17 27 25 34 3 23 17 7 8 33 2 10
32 37 44 52 47 40 44 15 8 13 9 36 27 18 44 28 31
38 3 2 27 48 27 14 5 12 3 52 2 24 6 11 30 51
27 8 29 21 47 30 14 26 51 44 12 25 19 16 53 39 10
32 47 1 46 2 53 11 20 40 33 35 17 3 47 45 51 38
23 36 2 34 5 2 8 27 2 22 26 29 39 28 43 19 37
32 30 31 44 16 11 5 23 37 31 45 45 8 43 7 31 15
18 12 16 15 54 2 2 3 52 21 7 2 37 15 46 2 17
43 31 28 6 25 18 11 31 26 53 19 45 24 8 30 35 45
2 55 42 32 3 1 33 2 26 32 43 34 21 24 56 12 30
22 3 47 7 2 6 5 27 43 15 40 27 23 4 16 22 2
Several symbols when removed increase repeats.
1 66
2 34
3 51
4 70
5 60
6 54
7 71
8 43
9 53
10 55
11 60
12 53
13 59
14 47
15 57
16 62
17 50
18 51
19 55
20 66
21 56
22 70
23 43
24 74
25 51
26 57
27 45
28 59
29 62
30 69
31 49
32 72
33 68
34 71
35 60
36 58
37 53
38 64
39 67
40 58
41 70
42 78
43 66
44 49
45 68
46 57
47 47
48 59
49 67
50 66
51 56
52 53
53 63
54 64
55 76
56 74
There about three dozen combinations, and some correlation between one symbol and two symbol results similar to the 340, but with more one symbol results.
Smokie55C. 61 symbols and 65 period 20 repeats.
1 2 3 4 5 6 7 8 9 10 11 8 12 13 14 15 16
17 18 4 19 20 21 22 23 24 25 26 27 19 28 29 30 27
22 31 32 14 33 34 35 12 1 6 29 35 36 37 38 39 8
40 5 2 41 42 4 9 43 44 45 40 32 14 34 12 46 1
39 7 5 17 47 42 39 48 33 44 49 50 1 41 12 19 15
4 51 6 52 45 36 43 37 20 53 29 1 12 32 54 55 10
2 27 12 34 20 15 12 1 46 56 23 6 17 21 5 8 43
13 23 39 52 28 25 21 29 40 42 51 12 31 57 54 18 2
35 34 58 33 34 3 12 5 4 11 39 31 50 16 20 6 19
24 10 8 29 44 9 35 13 32 35 52 41 27 45 50 51 34
6 15 27 59 11 19 52 9 18 22 40 12 11 14 43 12 3
25 1 31 60 13 28 29 54 10 29 23 6 17 35 57 28 36
55 20 54 2 19 42 34 36 50 12 41 7 8 6 56 31 26
21 52 37 54 6 61 32 49 27 41 37 43 30 10 45 33 25
5 36 1 16 39 38 34 7 45 14 12 28 23 31 51 12 33
3 55 2 20 57 29 29 10 8 1 11 14 6 7 34 45 56
19 52 54 59 61 47 12 38 23 4 46 5 7 27 14 56 17
25 61 53 54 6 13 39 42 18 24 51 12 9 35 16 29 49
26 12 3 2 55 32 21 21 12 36 44 49 34 20 42 37 11
12 14 9 7 31 54 57 5 59 33 41 60 39 34 12 17 29
No one symbol, when removed, increased period 20 repeats.
1 20
2 33
3 52
4 50
5 49
6 32
7 46
8 31
9 46
10 27
11 57
12 24
13 42
14 39
15 41
16 50
17 46
18 54
19 31
20 31
21 38
22 55
23 38
24 57
25 42
26 52
27 33
28 39
29 43
30 53
31 35
32 46
33 50
34 36
35 35
36 29
37 37
38 50
39 54
40 48
41 41
42 43
43 29
44 46
45 38
46 50
47 53
48 61
49 49
50 47
51 49
52 31
53 45
54 29
55 38
56 42
57 53
58 60
59 52
60 51
61 49
And no two symbol combination results in increase in repeats when removed. Smokie55B ( post above ) shows that there can be false positives with one and two symbol removals. Smokie55A and 55C show that there may also be no false positives with the detection.
Smokie56A has 60 symbols and 65 period 20 repeats. I transcribed around the nulls, which are in exactly the same locations as symbols 1 and 33 in the 340.
1 2 3 4 5 6 7 8 9 10 11 12 8 13 9 7 14
15 6 16 17 18 19 2 20 21 22 23 24 25 26 4 18 27
28 29 30 31 32 33 33 34 35 36 31 27 14 2 37 1 16
38 8 39 2 22 24 40 9 2 23 10 10 8 36 41 5 42
25 37 17 31 43 11 36 44 43 19 37 32 45 46 13 5 35
47 6 40 35 48 33 45 49 16 2 35 10 17 43 15 43 8
42 2 50 35 36 45 26 31 11 6 4 40 18 50 39 51 2
52 10 32 22 29 30 51 16 3 33 28 8 9 42 14 2 12
42 35 50 39 45 53 54 48 40 22 13 38 55 30 23 33 56
31 2 5 10 16 25 29 57 2 16 58 5 7 34 47 15 55
16 2 10 6 28 34 4 59 17 9 14 2 2 19 6 20 2
55 12 15 35 38 45 32 18 2 17 43 5 41 31 30 23 40
31 22 29 51 25 6 30 50 44 58 19 47 42 13 2 10 28
54 35 10 4 37 48 52 38 56 11 18 2 43 45 17 14 31
23 12 26 16 5 33 48 9 32 58 39 2 13 19 7 47 43
34 60 35 38 45 39 9 25 36 54 19 17 18 47 40 28 5
22 7 49 30 19 5 47 53 56 6 43 10 49 13 15 27 8
31 35 27 18 40 21 38 23 31 48 33 1 2 39 28 27 12
7 2 40 5 25 43 4 29 22 18 2 16 10 15 42 2 24
50 2 20 1 11 16 45 10 13 2 17 21 9 19 35 10 31
The nulls are symbols 1 and 27.
Detection worked perfectly this time. Removing either symbols 1 or 27 results in an increase in repeats.
1 68
2 28
3 59
4 46
5 47
6 48
7 56
8 48
9 42
10 39
11 48
12 53
13 49
14 42
15 50
16 37
17 39
18 51
19 35
20 56
21 59
22 50
23 47
24 63
25 44
26 56
27 71
28 49
29 53
30 44
31 40
32 51
33 44
34 53
35 42
36 54
37 50
38 61
39 48
40 44
41 62
42 53
43 54
44 53
45 44
46 55
47 50
48 50
49 61
50 52
51 57
52 61
53 64
54 58
55 54
56 63
57 61
58 60
59 59
60 65
This is fairly interesting. Here are the two symbol combinations that increase repeats, and the results are very similar to the 340 because each of the two symbols identified above share other symbols, that when removed in combination, increase repeats. In other words, 1 – 57, 1 – 60, 27 – 57, and 27 -60.
1 and 57
1 and 58
1 and 60
12 and 53
24 and 56
27 and 57
27 and 60
56 and 57
EDIT: There is only one each of symbols 57 and 60.
Thanks for the new ciphers and examination smokie.
In my experience. When using a AZdecrypt or bigram null heatmap, one way to tell that there are probably no more nulls is that when improvements flock to the start and/or end of the cipher. Skipping or adding symbols near the start and/or the end of the cipher does not disrupt the periodical transposition as much. Perhaps it is just that.