That looks interesting smokie, looking forward to your results. I would also like to examine some of the cipher and plaintexts.
Smokie, can you double check the polyphones for smokie33? Or share me the original cipher or plaintext.
Thanks
Only checking the polyphones will do, there is some sort of problem with the polyphone solver.
Okay, I fixed the issue with the polyphone solver but don’t understand why the smokie33 does not solve with your polyphone table since it only raises the multiplicity to 0.22058. Nevertheless I will give it another go now.
@Mr lowe, can you share the high bigram matrix?
Sorry about the delay. I wasn’t watching the site.
Smokie33 info:
Symbol 6 maps to three plaintext
Symbol 14 maps to four plaintext
Symbol 21 maps to two plaintext
Symbol 23 maps to three plaintext
Symbol 33 maps to two plaintext
Symbol 54 maps to four plaintext
Symbol 57 maps to two plaintext
This is the same info, and it is correct. I carefully checked it. Perhaps we have a misunderstanding. When I say that symbol 6 maps to three plaintext, I mean that it represents three letters of the alphabet. I can give you the plaintext and key if you want.
Okay, I fixed the issue with the polyphone solver but don’t understand why the smokie33 does not solve with your polyphone table since it only raises the multiplicity to 0.22058. Nevertheless I will give it another go now.
@Mr lowe, can you share the high bigram matrix?
Hopefully tomorrow.. It’s on my work computer..
This is the same info, and it is correct. I carefully checked it. Perhaps we have a misunderstanding. When I say that symbol 6 maps to three plaintext, I mean that it represents three letters of the alphabet. I can give you the plaintext and key if you want.
Yes, give me the plaintext and key please. I need to determine if the problem is the cipher or the solver.
In the homophonic substitution thread you mention 8 poly symbols:
O.k., Here is smokie33. There are 8 poly symbols with count of about 80 across the message. The plaintext is original. Cyclic substitution; no transposition.
21 46 1 35 10 33 2 50 11 14 30 26 6 27 39 57 51
23 40 34 15 33 4 10 16 54 4 7 41 52 19 47 61 22
48 42 58 54 13 5 17 18 20 59 28 55 24 8 49 57 53
25 14 14 14 15 10 43 16 44 45 17 46 55 14 54 54 52
55 18 23 47 62 56 23 6 38 9 39 48 38 54 40 49 55
26 31 30 1 51 27 35 6 41 14 35 42 28 31 19 14 30
11 26 34 34 14 12 26 2 56 14 6 62 60 24 16 36 13
3 33 23 20 48 61 58 37 54 27 32 51 6 28 21 25 55
32 62 8 47 6 52 43 57 14 48 61 14 38 44 4 45 16
49 56 40 33 14 6 53 23 26 32 6 54 2 8 41 54 59
27 55 23 22 48 42 57 54 14 21 14 15 19 9 14 1 46
50 14 30 61 52 24 47 17 13 12 18 13 6 25 14 14 10
2 48 7 23 15 16 52 17 8 24 39 23 44 18 10 49 14
12 40 35 27 40 36 9 25 42 44 45 17 10 56 42 33 3
54 39 4 37 14 53 23 14 16 10 11 17 10 46 18 13 31
14 2 20 32 15 55 54 58 7 16 57 54 17 47 16 14 23
48 18 50 38 41 23 16 43 43 18 49 51 60 6 54 24 21
14 17 18 38 56 1 6 14 52 2 57 7 14 56 25 17 35
3 6 54 16 14 38 1 56 17 29 54 32 1 45 18 37 41
53 33 26 56 23 47 14 10 54 2 9 39 52 3 57 6 15
I thought that it was 8 too, but checked and checked again. I don’t know what happened.
G R A N D M A S D E L I C I O U S
H O M E M A D E T A C O S F R Y G
R O U N D B E E F W I T H C R U S
H E D R E D P E P P E R T O T A S
T E F R Y T H I N C O R N T O R T
I L L A S I N C O R N O I L F O L
D I M M E D I A T E L Y W H E N D
A M P F R Y U N T I L S L I G H T
L Y C R I S P Y D R Y O N P A P E
R T O W E L S F I L L T A C O S W
I T H G R O U N D B E E F C O A R
S E L Y S H R E D D E D C H E D D
A R C H E E S E C H O P P E D R E
D O N I O N C H O P P E D T O M A
T O A N D S H R E D D E D R E D L
E A F L E T T U C E U S E R E D F
R E S N O P E P P E R S W I T H G
R E E N T A C O S A U C E T H E N
A L T E R N A T E J A L A P E N O
S W I T H R E D T A C O S A U C E
A 1 2 3 4 54
B 5 21
C 6 7 8 9
D 10 11 12 13 14
E 14 15 16 17 18
F 19 20 23
G 21 22
H 23 24 25
I 26 27 28 6
J 29
K
L 30 31 32 6
M 33 34
N 35 36 37 38 54
O 39 40 41 42 14
P 43 44 45 23
Q
R 46 47 48 49 14
S 50 51 52 53 54
T 54 55 56
U 57 58
V
W 59 60 33
X
Y 61 62 57
Z
21 46 1 35 10 33 2 50 11 14 30 26 6 27 39 57 51
23 40 34 15 33 4 10 16 54 4 7 41 52 19 47 61 22
48 42 58 54 13 5 17 18 20 59 28 55 24 8 49 57 53
25 14 14 14 15 10 43 16 44 45 17 46 55 14 54 54 52
55 18 23 47 62 56 23 6 38 9 39 48 38 54 40 49 55
26 31 30 1 51 27 35 6 41 14 35 42 28 31 19 14 30
11 26 34 34 14 12 26 2 56 14 6 62 60 24 16 36 13
3 33 23 20 48 61 58 37 54 27 32 51 6 28 21 25 55
32 62 8 47 6 52 43 57 14 48 61 14 38 44 4 45 16
49 56 40 33 14 6 53 23 26 32 6 54 2 8 41 54 59
27 55 23 22 48 42 57 54 14 21 14 15 19 9 14 1 46
50 14 30 61 52 24 47 17 13 12 18 13 6 25 14 14 10
2 48 7 23 15 16 52 17 8 24 39 23 44 18 10 49 14
12 40 35 27 40 36 9 25 42 44 45 17 10 56 42 33 3
54 39 4 37 14 53 23 14 16 10 11 17 10 46 18 13 31
14 2 20 32 15 55 54 58 7 16 57 54 17 47 16 14 23
48 18 50 38 41 23 16 43 43 18 49 51 60 6 54 24 21
14 17 18 38 56 1 6 14 52 2 57 7 14 56 25 17 35
3 6 54 16 14 38 1 56 17 29 54 32 1 45 18 37 41
53 33 26 56 23 47 14 10 54 2 9 39 52 3 57 6 15
Thank you.
I see now, it is a perfectly fine but low scoring plaintext. The ngrams that we use (practical cryptography, reddit and usenet) do not match your plaintext well. It is like daikon’s cipher about the star constellations but even harder. I am happy that there is no additional problem with my polyphone solver but such a plaintext is a humbling experience.
The message is a recipe for tacos. I would like to see your solution. But I wouldn’t be too humbled. After all, you did write a computer program that solves homophonic substitution ciphers with multiple polyphones. That’s pretty amazing.
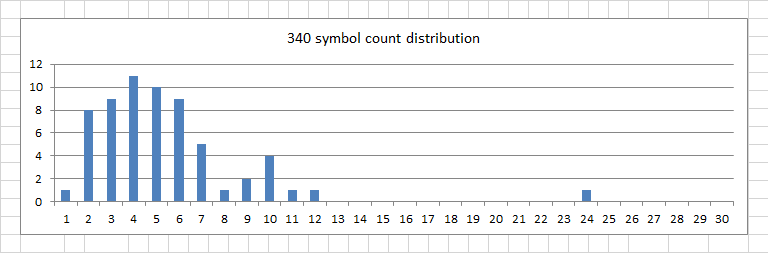
Zodiac 340 Symbol Count Distribution
Note only one symbol with count of 1, but eight symbols with count of 2. Several symbols with count of 9 or more.
Statistics ( does not include the + symbol )
Mean count = 5.2
Standard Deviation = 3.8
Mean + STD = 9.0
Mean – STD = 1.3
This is kind of important for making messages. I want to simulate the 340 as much as possible, and if I pack 63 symbols evenly ( least efficient ) into + / – 23 plaintext on the key, then I get more bigram repeats but also more symbols with count of 1. If I make the key efficient, then low frequency plaintext will have fewer symbols. The bigram repeats goes down, but the number of symbols with count of 1 goes down. So it is a delicate balance.
Hi Jarlvie this is one of them. I will dig out the other I have misplaced it.
._5&:X[$Z%/SC[ML
S9HUIZ)V<IKY4C:2[
$KW#’MWWOC"OA*G6
‘FTAK%?#CM.8’7%N]
E.J;L97*_4<FK-DQ%
+-9#CQ;U>C">2?C?F
1>C#9O#C.NOCCN_4"
6->3/77EJ]3G:2′)O
XC1QNR/B%ED?!,/1
!@;+:=EP6CMZ.Y$4
4#E93!A49]05J#MDR
017^C4]17P!@>CX:^
8-(Z.#,H-O&4R99N#
C5)C4$^C4V&’8QZ.,
;U"’GC’CEG)>1/Y27
/2.’S]0WM2NN$3(KC
W#6–C"I5N#7X3’A2
R;S>’1.J;"97_6CE7
:%]04%M=EP<FTA$KS
49N_R*E-S[C[!NUI
This is kind of important for making messages. I want to simulate the 340 as much as possible, and if I pack 63 symbols evenly ( least efficient ) into + / – 23 plaintext on the key, then I get more bigram repeats but also more symbols with count of 1. If I make the key efficient, then low frequency plaintext will have fewer symbols. The bigram repeats goes down, but the number of symbols with count of 1 goes down. So it is a delicate balance.
One simple way to emulate/simulate the repeat potential of the 340 or any cipher without reusing the exact same frequency table is to match the raw ioc closely. It is 2236 for the 340.
Here’s how the calculate the ioc:
340 frequencies + ioc calculation: - first numeric value for each symbol is its frequency - second numeric value is its frequency minus 1 - symbols with a frequency of 1 get a value of 0 because they cannot repeat +: 24 * 23 = 552 B: 12 * 11 = 132 p: 11 * 10 = 110 |: 10 * 9 = 90 O: 10 * 9 = 90 c: 10 * 9 = 90 F: 10 * 9 = 90 2: 9 * 8 = 72 z: 9 * 8 = 72 R: 8 * 7 = 56 l: 7 * 6 = 42 (: 7 * 6 = 42 K: 7 * 6 = 42 M: 7 * 6 = 42 5: 7 * 6 = 42 ^: 6 * 5 = 30 V: 6 * 5 = 30 L: 6 * 5 = 30 G: 6 * 5 = 30 W: 6 * 5 = 30 .: 6 * 5 = 30 <: 6 * 5 = 30 *: 6 * 5 = 30 4: 6 * 5 = 30 k: 5 * 4 = 20 T: 5 * 4 = 20 d: 5 * 4 = 20 N: 5 * 4 = 20 #: 5 * 4 = 20 ): 5 * 4 = 20 y: 5 * 4 = 20 U: 5 * 4 = 20 -: 5 * 4 = 20 C: 5 * 4 = 20 H: 4 * 3 = 12 >: 4 * 3 = 12 D: 4 * 3 = 12 Y: 4 * 3 = 12 f: 4 * 3 = 12 Z: 4 * 3 = 12 J: 4 * 3 = 12 S: 4 * 3 = 12 8: 4 * 3 = 12 9: 4 * 3 = 12 t: 4 * 3 = 12 E: 3 * 2 = 6 P: 3 * 2 = 6 1: 3 * 2 = 6 7: 3 * 2 = 6 _: 3 * 2 = 6 /: 3 * 2 = 6 ;: 3 * 2 = 6 b: 3 * 2 = 6 6: 3 * 2 = 6 %: 2 * 1 = 2 :: 2 * 1 = 2 3: 2 * 1 = 2 j: 2 * 1 = 2 &: 2 * 1 = 2 q: 2 * 1 = 2 X: 2 * 1 = 2 A: 2 * 1 = 2 @: 1 * 0 = 0 summed total: 2236 (the raw ioc) normalized: 0.0193996182543814 = 2236 / (340 * 339)
Hi Jarlvie this is one of them. I will dig out the other I have misplaced it.
Thanks for sharing, what kind of pattern did you follow?
Hey thanks for sharing the raw ioc information. The values used to calculate the raw ioc are the same ones that I have been trying to match. I will add that to my encoder and find a way to use it.
I think its this method I will check it tonight I made two of them similar. odd ""COLUMNS"’ then even COLUMNS then each COLUMN up one period from the next. then read from top down.