The message is a recipe for tacos. I would like to see your solution. But I wouldn’t be too humbled. After all, you did write a computer program that solves homophonic substitution ciphers with multiple polyphones. That’s pretty amazing.

It’s a beatiful message. I developed the polyphone solver near the end of 2016 and ran it with an external hill-climber that distributes a given number of polyphones (extra letters) over the symbols. After days of running it found the following plaintext as a best result, you can see that it is in the right direction. It just is a very hard plaintext.

31/12/2016

GRANDSASHEWILLINS
TOMISSDESSIONTHEP
ROVEDHEEUWUBTCRNS
HESAIDGETHERBROWN
BETHATTONWIRNFORB
ITWASLABOUTOUTTOW
HIMMEDIATEDATTEND
ASTURESPELLSOUGHB
LACHINGNOREANTSHE
RTOSAYSTILLYACOOW
LBTPRONGAGEITWEAR
STWENTHEDDEDTHEAD
ARITIENECTITTEDRE
DOLLONWHOTHEDTOSA
YISPOSTHEDHEDREDT
HAULIBERIENCEHEST
RESNOTEGGERSTHATG
REENTAEONANINTHER
ALTERNATEOFLAHEPO
SSITTHEDRAWINANCI

Briefly hijacking this thread: Can you guys give a second opinion for a solve of the Albany cipher?

http://www.zodiackiller.net/viewtopic.p … 742#p52742

Sure doranchak,

Can you share a ciphertext and solution? The thread confuses me.

I’ll post it there.

Spreadsheet Encoder Statistics

I briefly suspended my digraph – transposition – homophonic message making. I made 200 of these messages, and 200 transposition – homophonic messages, but realized that I may be comparing apples to oranges instead of apples to apples because I was guessing with my encoder variables to try to emulate 340 stats.

So I re-tooled my encoder so that I can encode 16 messages at a time. The encoder works like this. It makes a key, depending on letter count, on four different efficiency settings. 1 = most efficient to 4 = least efficient diffusion.

And I can make the spreadsheet map a polyphone ( or more ) to 0 to any count of highest frequency plaintext.

I made 16 messages for each of the Jarlve 100 plaintext library ( I changed message 24 because it was exactly the same as message 23 ). Four different efficiency settings * four polyphone settings = 16 messages * 100 = 1600 messages. All perfect cycles.

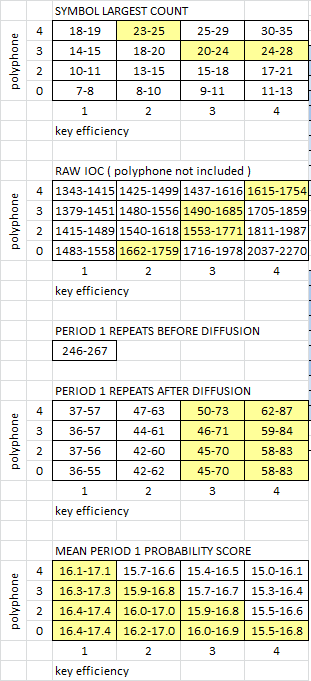
Here are the stats.

1. Top table shows the polyphone symbol count. X axis is the key efficiency, Y axis is the number of highest frequency letters that I mapped the one polyphone to. For the bottom row, I did not use a polyphone. Then the next row up, I mapped one polyphone to the two highest frequency letters. And so on. The Zodiac 340 has the + symbol with count of 24. Yellow shaded areas show the key efficiency and polyphone mapping match up ranges, mean + standard deviation, that the 340 would fall in.

2. Second table shows the RAW IOC calculated without including the polyphone. The bottom row does not reflect a polyphone. Even though 1200 messages for the top three rows had one polyphone, the existence of the polyphone did change the stats. The 340 RAW IOC is 1684 if you do not include the + symbol. IOC for a homophonic substitution message is IOC for a homophonic substitution message I guess.

3. The third table, one cell, shows the count of period 1 bigram repeats in the plaintext, which would become period x repeats in a transposed message.

4. The fourth table shows the count of period 1 bigram repeats after diffusion. The yellow shaded cells show that it is easier, by far, to make messages with 340 period 15 / 19 stats with an efficiency setting of 3 or 4. But the 340 is at the higher end of the setting 3 range. It is much easier to match 340 stats with the setting 4, a very inefficient key.

EDITED:

5. The fifth and bottom table shows the average of the period 1 repeat probability scores. This is the one that I am interested in because the 340 period 15 / 19 score is 16.8. More efficient keys cause more diffusion, but there will be some repeats that drive up the score because there are not very many symbols mapping to lower frequency plaintext. Like this one. The idea regarding digraph – transposition – homophonic is that the digraph diffusion makes it so that the homophonic key has 26 letters to encode, not typically 22-24. The 63 symbols would be distributed more evenly, making more of these, driving up the score. The 340 period 15 / 19 repeat score of 16.8 ranks 2nd of all periods. The idea is that a digraph – transposition – homophonic will have higher ranking scores. He could have drafted the message vertically in 15 or 19 columns, encoded with a digraph cipher, then re-drafted into 17 columns and then encoded homophonic.

EDIT: The more efficient keys make messages that have higher average period 1 repeat probability scores because it causes more repeats like this one.

So any time that I want to try a new cipher, I need to do this for the cipher type first, so that I know what settings to use.

Unfortunately, there is no cell that is shaded yellow in all of the tables. But standard deviation only covers about 2/3 of the possible range. Efficiency setting 3 with one polyphone mapping to 3 plaintext comes the closest, but the standard deviation range for repeats still barely reaches 340 stats.

Digraph Experiment Resumed

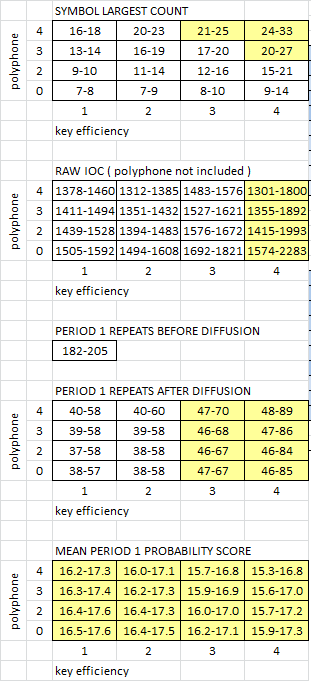
I make 1600 messages digraph – homophonic ( no transposition, perfect cycles ) to figure out what settings to encode a digraph cipher with to match 340 stats.

1. First table, I should use key efficiency of 3 or 4, with one polyphone mapping to 3 or 4 plaintext to simulate the +.

2. Second table, I should use key efficiency of 4 to get a RAW IOC, not including the +, to match 340 stats.

3. Third table which is only one cell, count of period 1 repeats are down, obviously, because of digraph encoding.

4. Fourth table, a key efficiency of 3 barely meets 340 stats, key efficiency of 4 easily done.

5. Fifth table, this is what I am talking about. No matter what the key efficiency or the polyphone mapping, the average probability score of the period 1 repeats match 340 stats.

Hey smokie,

Can you share 1 digraph + homophonic substitution cipher that has no further complications so that I can start thinking about a specific solver.

Thanks

Message 34

W E H A V E C O M P L E T E D O U
R A S S I G N M E N T T O T H E B
E S T O F O U R A B I L I T Y S U
B J E C T T O T H E L I M I T A T
I O N S O F T I M E A N D R E S O
U R C E S A V A I L A B L E T O U
S O U R C O N C L U S I O N S O F
F A C T A N D O U R R E C O M M E
N D A T I O N S A R E U N A N I M
O U S T H O S E O F U S W H O D I
F F E R I N C E R T A I N S E C O
N D A R Y R E S P E C T S F R O M
T H E F I N D I N G S S E T F O R
T H H E R E I N D O N O T C O N S
I D E R T H E S E D I F F E R E N
C E S S U F F I C I E N T T O W A
R R A N T T H E F I L I N G O F A
M I N O R I T Y R E P O R T I T I
S O U R E A R N E S T H O P E T H
A T T H E F R U I T S O F O U R D

Random digraph chart. Sorry about the mess. If you want to encode the first two plaintext of the message, WE, the digraph would be at the intersection of the 23rd row and the 6th column, EA. If you want to encode the next two plaintext HA, the digraph would be at the intersection of the 8th row and 1st column, YD. Etc.

LA CV UI PG HF DJ VV NW MU MS PD RY LR AT OP LF RK KF OH IM JO HX GY CE MC XA
HN KN CU XZ HA VG QL MU LK DF CC VE HQ OT LX FD BT BH WU XN DI FE RB XQ IP OL
CO WW EW XD KO FR QK LH KH RL TO OR LL MR BE RV EF NN AO FJ DZ IT WI LT EK LA
JF MV AC LD QL AE CX PJ GV LP NJ SQ AI RW LQ QG ZE LE KI LV AI AN BY LF LH SH
EX IY EX KA KZ DW IL UB UI OW EQ EP UJ WF KL RP ZE BJ FG IU DR DZ DE NG JZ ZI
XY HK ZG WJ CH GH PQ FZ LJ RS LC UO BY AE NC SI DG ZJ UD TS MY UP ZU KS XX ZL
GF FN ZD FS SZ UI IH BB VK VG FW GD TC SN FY AD UU SX WU CC MY KR EA FX YF WB
YD PG PS PU TE DB CM BY WT EU OW CO KQ QC CT HL YN MO SP BG IO FU SH YD VS GK
VE QJ IT AF SP FH QM IR SO XQ FK PI IJ SQ MJ QR AW DS UV TO YS WA FD FN HB XK
FI GN HD VQ SX IQ ES AL ED RT VB US SE YC LX CY XY ZW JN SN OV WL RO MO DC DT
ZR KV PI BJ VA JJ GF NP JW TZ NL VQ EF VA MX JH PT RX LN QG HJ MC DX VZ VU US
ZE CY IN QJ CS NV TA QT GH CU NE OP UJ IE EW TH JR VF AQ TR JT MM HW MP EM EZ
NM MV OX BP JQ PU QF NR UW MN NW HP JD IM UF RV JM OM DH HC KZ PB HB NK YP PC
BY YY YG GP NI BK YK SZ OV XA SQ AV MI FS XE AN VG UJ RW HK EG YZ DT OI VT VZ
NN CG PU QT JJ TE ZS KC TX ZA EU CJ QI JS CH IH PE XY HU LR XA CH DA GL GF VC
XM OL JY WD KM HX NX YZ EZ BR AG IV WB FT LZ YA WW GF GL XF RM DO TR QN EV QI
BY EP NN MD JR GC VU YQ LB HB ER DS RP SR IT FO WJ LT XC XK JJ RL KB XQ BO YQ
YY FO OJ NO BB GI AS IP PB NF UC KL NS PX ZB FB XA VM QH OG CP GU BV US UL KM
XM YI WP SU JP GV UB RM JS PZ TS WH RV VV AG SW WC MY RM EO ZA MD RZ IK GV CK
GP QB VM OB GT ZW AQ PM OQ KX IZ LK DK QQ AO OY HB KI CT ZQ GV WW BE MD BY WR
UL FW OK NG CF SU HL TM UF BM GD AX QL KW ZS LO AA OC KK HL PY PB WZ TY QN AV
FJ SH JS MH DA WU YR RX KR TQ UZ TD XK JY ZK RL IK IC YR PH QL SG YE BO VQ YG
WT GG ZR KF EA VL YU JG JE HW OE ZT BQ TD TP QD SN EO BV OR MO CH VL PK UT DI
FX SK NQ FK ZA HZ TE TU AC BB ZN HM QO SD DM XC JP PA TS TN YM MT NE EN DI ZA
XH UD RW IU NW RX TH MB KZ JN HC GA NX ZI TD OY BA TR XO DP DI IA QV WG ZD AM
HX WG XW GF KS WB NX RV CN YR PG RJ OU WZ SZ AJ CB YT QF PC UC EE II JF YP OM

Digraph encoded message

E A Y D D A B E R V C S G T L Q O
C O H J S S N J Q H K A O P M I Y
F G A O N C O C C V P I T O X O F
W S X F J A O P M E P I J T O I M
M J R W T E O Q J Q A T L E F G X
A O J F G H X M U Z E V E I U X A
A G O C B E Y G J T J S J S A G G
H U I G P G P X A V M E X Q I J Q
G P I M M J R W K F D R B Y O V U
F K K P M H U K L M Y R Z C T G V
G H B J S Q K O O G M U R W E X J
S J F U L B B S W E X C T Z J Q I
P M D W S Q G V Y K R M I U N C O
G B Y B J U I G P J S L R B E R W
A F B J P M F G K A F H C H B B Y
G F G Z A G H I T S P H K A O W T
V M A T Z Q T E L J G H Y K T E L
R S Q X Y T O T R R P X Y O Q O Q
A G O C E X P X F G P M I H I U Y
D Z Q T E Z J U F C T T E X A N O

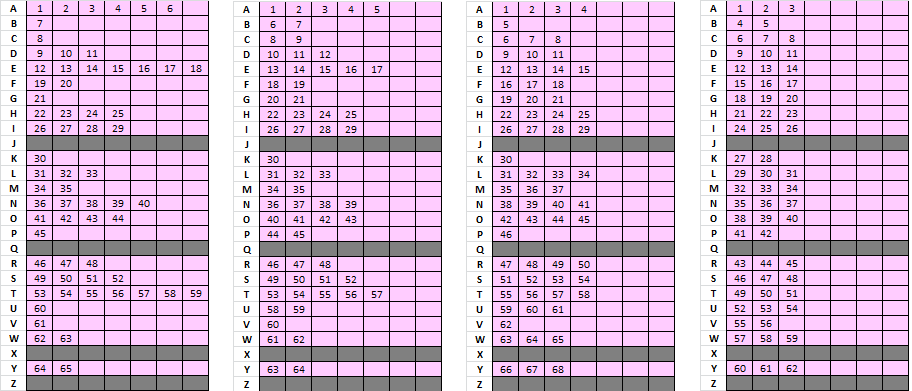
Homophonic key with symbol 15 mapping to 4 letters.

A 1 2 3 15
B 4 5
C 6 7
D 8 9
E 10 11 12
F 13 14
G 15 16 17
H 18 19
I 20 21
J 22 23 24 15
K 25 26
L 27 28
M 29 30 31
N 32 33
O 34 35 36 15
P 37 38
Q 39 40
R 41 42
S 43 44
T 45 46 47
U 48 49
V 50 51
W 52 53
X 54 55
Y 56 57
Z 58 59

Homophonic message

10 15 56 8 8 2 4 11 41 50 6 43 15 45 27 39 34
7 35 18 22 44 43 32 23 39 19 25 3 36 37 29 20 57
13 16 15 15 33 6 34 7 6 51 38 21 46 35 54 36 14
53 44 55 13 24 1 35 37 30 12 38 20 15 47 34 21 31
29 22 42 53 45 10 35 39 23 40 2 46 28 11 14 16 54
3 36 22 13 15 18 55 30 48 58 12 50 11 20 49 54 15
1 16 15 7 5 11 56 16 15 47 15 44 23 43 2 16 16
19 48 21 17 37 15 38 55 3 51 31 12 54 39 21 24 40
16 37 21 29 30 15 41 52 26 14 8 42 4 57 34 50 49
13 25 26 38 31 18 48 26 27 30 56 41 59 6 47 17 51
15 18 5 22 43 39 26 35 36 16 30 49 42 53 10 55 23
44 24 14 48 27 4 5 43 52 11 54 7 46 58 15 39 20
37 31 9 53 44 39 17 50 56 25 41 29 20 49 32 6 15
15 4 56 5 22 48 20 16 38 23 44 27 42 4 12 41 52
15 14 5 24 37 30 14 17 25 1 13 18 7 19 4 4 57
15 14 15 59 2 16 18 21 47 44 38 19 25 3 34 53 45
50 30 15 46 58 40 47 10 28 15 15 18 56 26 45 11 27
42 43 39 55 57 47 35 47 41 42 37 54 56 36 40 15 39

The digraph chart is randomly generated for this experiment. A playfair, four square or two square generated digraph chart would have some different characteristics. Let’s say you want to encode the plaintext TH from digraph chart generated by one of those ciphers. T may map to A, but T may also map to A if the plaintext was TR if H and R are in the same column in the playfair, foursquare or two square encoding worksheet. But if you could hill climb the chart that is generated from the worksheet, then you wouldn’t have to guess what type of digraph cipher it is.

Just think about it a little bit. I am still working on the experiments. I had some trouble with my homophonic encoder with 26 letters and efficiency setting 4, which I just found out about because it wasn’t using enough symbols. However, it is still possible to generate the right count of repeats with efficiency setting 3 and one polyphone mapping to 4 letters. But only about 3% of the time I think. EDIT: DELETE COMMENT AND WAIT FOR RESULTS { Maybe a little more, but the average period x repeat probability score will almost always rank #1 or #2 }. After this I am going to work on figuring out other ways to detect the difference between a homophonic and digraph + homophonic.

Thanks smokie for the detailed report and inclusion of plaintext and tables, I will think about it.

O.k., I finally have my results. I made 200 digraph – scytale – homophonic, and 200 scytale – homophonic.

Here is smokie57. It is message 70, written vertically into 19 columns, encoded with the digraph chart, and scytale re-drafted into 17 columns ( to presumably hide the repeats ).

Then encoded homophonic. I have the digraph chart and homophonic key if you ever need it.

20 35 31 54 52 22 49 44 36 21 32 57 55 15 29 49 33
58 38 16 2 31 30 22 25 15 54 37 25 16 53 21 42 15
15 17 52 3 22 9 57 24 7 27 50 53 45 40 42 23 57
10 9 22 12 9 58 5 23 22 25 41 19 44 23 6 4 18
17 59 20 24 8 21 13 22 57 29 45 35 27 28 23 9 9
27 11 39 32 27 7 40 52 18 21 36 15 54 9 29 44 31
28 10 21 42 3 32 21 9 4 58 11 25 37 59 24 9 26
19 41 27 55 57 28 12 9 2 29 1 16 52 8 13 9 25
10 56 15 20 21 30 35 43 11 42 36 51 9 31 46 20 29
48 37 26 9 23 52 38 9 4 27 24 58 14 39 10 28 9
12 16 11 9 54 34 5 49 43 32 45 20 25 4 10 16 47
33 11 10 13 26 14 1 16 57 1 38 35 9 30 31 21 55
55 9 25 7 50 55 34 10 48 51 36 37 17 9 3 15 32
55 12 19 25 24 56 2 54 11 16 55 40 56 20 35 53 44
18 57 54 39 33 4 58 34 52 21 8 6 29 3 46 25 36
23 5 9 37 9 58 17 13 22 10 57 38 50 18 11 14 41
47 27 9 40 9 40 8 53 55 31 23 28 30 43 45 29 32
9 44 43 42 14 4 12 3 9 54 26 27 6 33 51 39 22
31 35 34 8 13 5 30 13 28 9 44 17 44 28 1 10 43
6 59 32 36 45 40 11 48 27 11 33 10 45 11 41 19 31

Here are the results. 25% random symbol selection.

Homophonic efficiency setting at 3 with one polyphone mapping to 3 letters.
Digraph + homophonic efficiency setting at 3 with one polyphone mapping to 4 letters.

Zodiac 340 = 67. There were 27 homophonic messages with 67 or more, or 13-14%. There were 15 digraph + homophonic with 67 or more, or 7-8%. That is about half, and that makes sense because some of the bigram repeats are destroyed but some false repeats are created.

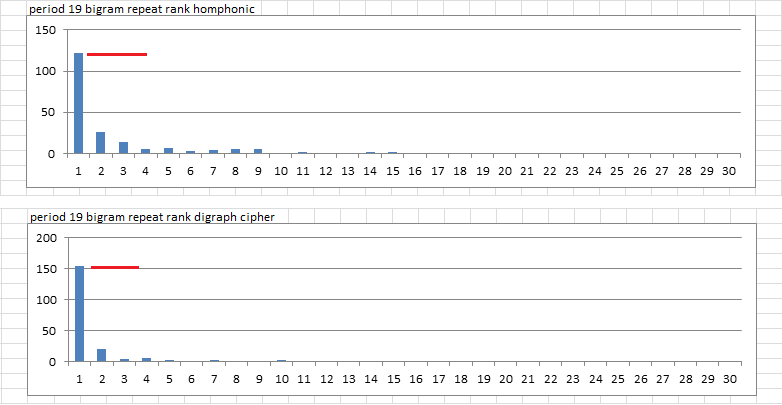
This is how the period 19 repeat spike ranked compared to all other periods 1-169.

With homophonic, there were 122 messages where the period 19 repeat spike was taller than all of the other spikes, or about 61%. That means that after strictly homophonic diffusion, there were 78 messages that had spikes at other periods that were taller than the spike at period 19. It does not mean that the spikes were at 340 stats of 67 repeats, but they were taller than period 19.

With digraph + homophonic, there were 155 messages where the period 19 repeat spike was the tallest, or about 77-78% of the time.

Here are three keys efficiency 1 – 3. I made the digraph + homophonic with the flattest key setting on the right. It seems that distributing the symbols more evenly causes fewer false spikes.

And distributing symbols more evenly causes the average repeat probability scores to go up.

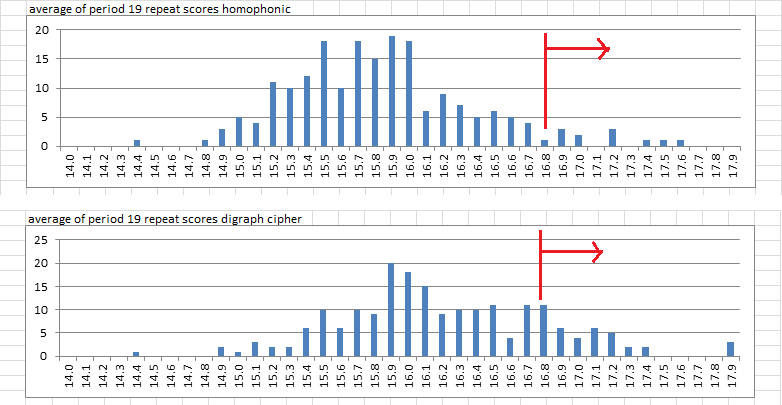
Zodiac 340 value is 16.8. For homophonic, there were only 12 messages, or about 6%, with score of 16.8 or higher. For digraph + homophonic, there were 39 messages, or about 19 20% with score of 16.8 or higher.

So with homophonic, there were more homophonic messages with period 19 spikes comparable to the 340, and more digraph + homophonic with average repeat probability score comparable to the 340.

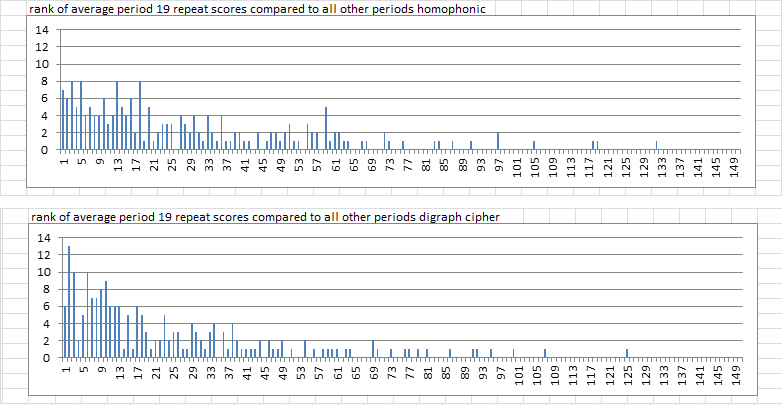
Here is how the period 19 average repeat probability score ranked compared to other periods 1-169.

The 340 period 19 spike is rank #2. There were 13, or about 6-7% of 200 transposition messages with rank of 1 or 2. There were 19, or about 9-10% of 200 digraph + transposition messages with rank of 1 or 2. This stat favors digraph + homophonic.

EDIT: Summary.

Period 19 repeat spike: Favors homophonic.
Rank of period 19 repeat spike: Favors digraph + homophonic.
Average period 19 repeat score: Favors digraph + homophonic.
Rank of average period 19 repeat score: Favors digraph + homophonic.

That is probably it for today. It is fairly easy to make a digraph + scytale + homophonic that closely matches 340 stats.

Next project is to explore odd versus even position biases for repeats in digraph ciphers. Preliminary work shows that there is a strong bias toward odd versus even for a digraph cipher, and also a digraph + homophonic cipher. More so than the 340 for period 19, which shows a slight bias. But I am thinking of exploring in more detail and will post.

Next project is to explore odd versus even position biases for repeats in digraph ciphers. Preliminary work shows that there is a strong bias toward odd versus even for a digraph cipher, and also a digraph + homophonic cipher. More so than the 340 for period 19, which shows a slight bias. But I am thinking of exploring in more detail and will post.

good work smokie
This is odd even columnar all the odd then all the evens then a rise of one each column. I think this is what you mean by bias. Can you dump it on your graph for me to see how it looks.

._5&:X[$Z%/SC[ML
S9HUIZ)V<IKY4C:2[
$KW#’MWWOC"OA*G6
‘FTAK%?#CM.8’7%N]
E.J;L97*_4<FK-DQ%
+-9#CQ;U>C">2?C?F
1>C#9O#C.NOCCN_4"
6->3/77EJ]3G:2′)O
XC1QNR/B%ED?!,/1
!@;+:=EP6CMZ.Y$4
4#E93!A49]05J#MDR
017^C4]17P!@>CX:^
8-(Z.#,H-O&4R99N#
C5)C4$^C4V&’8QZ.,
;U"’GC’CEG)>1/Y27
/2.’S]0WM2NN$3(KC
W#6–C"I5N#7X3’A2
R;S>’1.J;"97_6CE7
:%]04%M=EP<FTA$KS
49N_R*E-S[C[!NUI

I don’t know if we are talking about the same but some days ago I’ve also recognized a significant increase of bigrams and trigrams when sorting the columns by odd/even.
First, take all the odd columns and then take all the even columns. Now put them side by side. You will get 44 repeated bigrams and 5 repeated trigrams after period 18 is applied. I think it is obvious why period 19 from the original cipher gets period 18 in the odd/even sorted one. It’s just a „geometrical“ fact. The sorted one just behaves like a diagonally transposed cipher….but there is still no solve. Anyway….I’ll have a closer look into it.