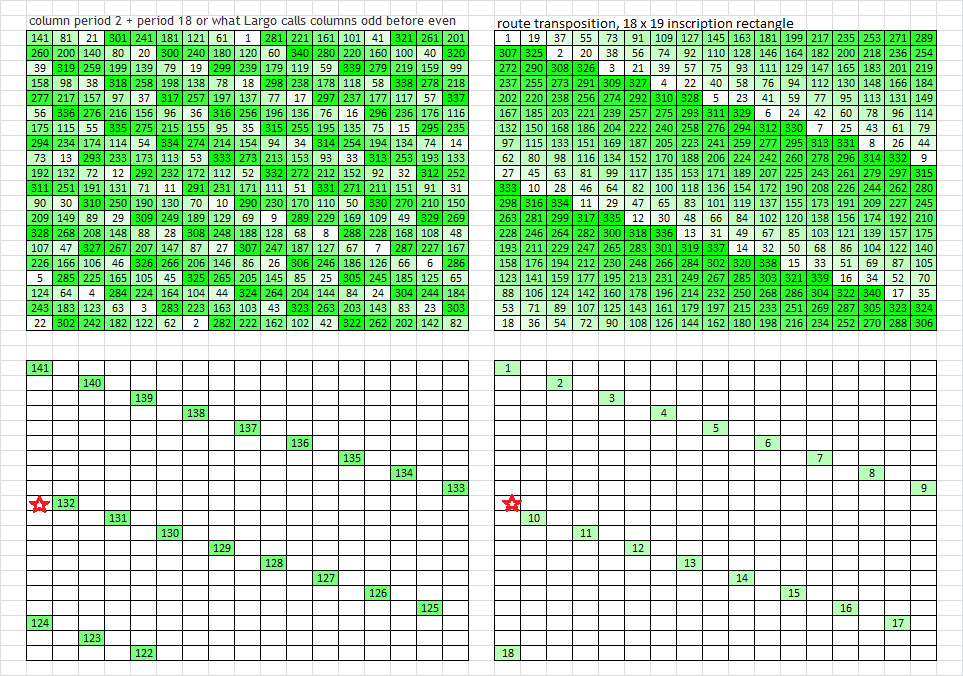
Try this transposition matrix, it creates a period 19 bigram cipher with a guaranteed better peak at column period 2 + period 18 or what Largo calls columns odd before even. The matrix is based off the magic square found in the Zodiac FBI files and the reading rules differ from the regular periodic transpositions we have been considering. For the record, columnar, diagonal and skytale transposition do not seem to produce this behaviour.

141 81  21  301 241 181 121 61  1   281 221 161 101 41  321 261 201
260 200 140 80  20  300 240 180 120 60  340 280 220 160 100 40  320
39  319 259 199 139 79  19  299 239 179 119 59  339 279 219 159 99
158 98  38  318 258 198 138 78  18  298 238 178 118 58  338 278 218
277 217 157 97  37  317 257 197 137 77  17  297 237 177 117 57  337
56  336 276 216 156 96  36  316 256 196 136 76  16  296 236 176 116
175 115 55  335 275 215 155 95  35  315 255 195 135 75  15  295 235
294 234 174 114 54  334 274 214 154 94  34  314 254 194 134 74  14
73  13  293 233 173 113 53  333 273 213 153 93  33  313 253 193 133
192 132 72  12  292 232 172 112 52  332 272 212 152 92  32  312 252
311 251 191 131 71  11  291 231 171 111 51  331 271 211 151 91  31
90  30  310 250 190 130 70  10  290 230 170 110 50  330 270 210 150
209 149 89  29  309 249 189 129 69  9   289 229 169 109 49  329 269
328 268 208 148 88  28  308 248 188 128 68  8   288 228 168 108 48
107 47  327 267 207 147 87  27  307 247 187 127 67  7   287 227 167
226 166 106 46  326 266 206 146 86  26  306 246 186 126 66  6   286
5   285 225 165 105 45  325 265 205 145 85  25  305 245 185 125 65
124 64  4   284 224 164 104 44  324 264 204 144 84  24  304 244 184
243 183 123 63  3   283 223 163 103 43  323 263 203 143 83  23  303
22  302 242 182 122 62  2   282 222 162 102 42  322 262 202 142 82


ebceetowilaeaiado
asmtevirtgyippdtn
iyrkssbadelnrktxt
esnmaceeelitlites
vegouupovrlsntall
llabnmfonrirpyeef
boiiheiehyirgoomh
ewnlkwihlhcenugfe
epmteanuetltuvron
yihgoavmaohlismio
gbghtncheihytrrio
nstentnietsntelih
gtasorieilbsiansl
uaatminetmellitsu
ufadhsetlbtomilti
ieoecntosillesaki
ewfcrreaimueilglg
ldkdoneobeweaswin
wailietegmecfhcui
asihkillrrnsmifte

I describe this as a guy back in 1969 with a pencil and paper writing the message at an angle, but not dropping down a row when crossing over from column 17 to column 1. On left is your matrix, on right is a matrix made by a route transposition using a 18 x 19 inscription rectangle. Then below I took out all symbols except for one angled row for better visualization.

If I cut column 17, scroll the message to the right, and paste it into column 1, your matrix continues the angled row, but the route transposition matrix angled row is misaligned. Two iterations of this.

Two more iterations. There are vertical misalignments, and horizontal misalignments created when scrolling the route transposition message, but not with your matrix. I have started a spreadsheet to explore this for detection, have to do some stuff today but definitely will continue with it very soon. We should be able to scroll the message and see what happens to detect what type of message it is.

Here is the result of a scrolling experiment.

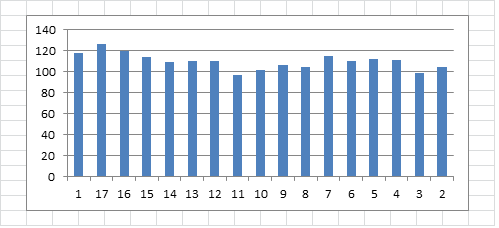
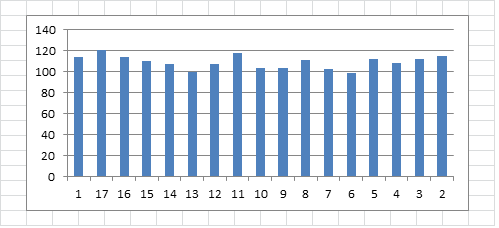
Here is the 340. X axis is the leftmost column ( 1 means undisturbed message, 17 means 17th column shifted to the leftmost position, etc. ). Y axis is the count of cells highlighted because they are part of a period 19 repeat. For the 340, Y varies between about 100 to 120.

I LIKE KILLING using Jarlve’s first matrix. Y varies between about 100 to 120.

11 5 7 12 13 50 40 58 22 28 1 14 2 23 3 10 39
3 46 33 51 15 57 24 45 52 18 61 25 42 43 9 52 34
22 62 44 26 47 48 6 1 9 11 28 35 44 27 52 60 51
12 49 36 33 1 8 13 14 15 30 22 52 31 23 53 11 46
56 12 19 40 54 55 42 41 56 45 11 46 37 51 3 28 29
30 31 4 5 34 32 16 40 35 44 24 45 43 61 13 14 17
6 39 25 11 20 14 23 11 21 62 22 44 18 40 41 33 20
12 59 36 11 26 58 25 21 28 20 7 13 37 54 18 16 14
15 43 32 50 11 2 34 55 11 53 31 53 55 57 45 40 35
61 11 21 18 39 2 56 33 3 40 20 30 11 48 32 22 41
18 5 18 21 51 36 8 20 13 23 21 62 51 45 45 24 38
37 49 52 14 34 53 35 25 15 50 47 36 51 15 28 11 20
19 52 4 47 39 45 22 14 23 11 6 48 24 1 37 49 28
55 2 3 51 33 25 34 13 50 32 14 29 30 11 51 47 55
55 17 4 9 21 49 15 52 31 5 53 40 33 22 31 50 23
25 11 41 12 7 35 51 38 48 11 29 30 14 49 4 27 23
14 59 17 7 45 44 15 2 25 32 55 11 23 30 18 31 19
11 9 26 10 41 37 12 40 6 13 58 14 3 47 59 23 37
58 4 25 28 11 15 52 15 18 33 12 7 17 21 8 55 23
1 47 23 21 27 24 29 30 45 44 36 48 32 25 16 53 13

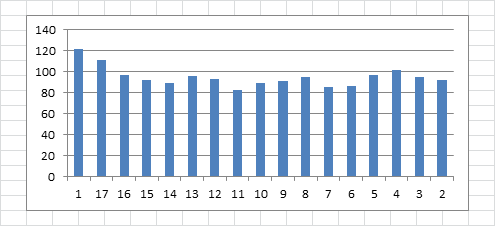
I LIKE KILLING using route transposition with an 18 x 19 inscription rectangle. Y varies between about 80 to 120. Scrolling disturbed a lot of the repeats.

24 5 54 23 11 24 1 38 32 12 50 26 13 20 44 51 6
28 13 29 13 34 30 16 47 35 33 39 34 21 47 48 11 37
20 12 34 8 25 8 11 31 38 52 22 13 49 7 2 41 53
35 23 14 8 38 3 27 1 50 24 45 21 32 51 52 15 37
17 42 25 37 24 39 53 55 11 54 23 34 45 12 1 20 50
23 18 16 2 9 42 21 33 19 46 26 48 48 18 13 32 11
24 20 51 14 58 44 22 1 4 15 11 12 22 12 33 59 49
40 41 35 44 23 52 24 52 13 45 56 32 57 61 28 25 38
23 50 47 17 19 22 47 51 52 39 23 1 14 62 15 40 29
50 44 11 5 50 2 18 31 11 24 20 16 58 10 27 48 61
55 25 11 12 9 15 10 11 22 28 56 36 3 23 24 25 11
29 41 59 37 49 17 19 7 4 30 57 22 11 18 19 51 31
8 31 4 54 23 19 49 55 3 3 34 53 11 35 36 62 22
25 28 11 29 56 33 30 42 38 36 32 54 19 39 47 18 6
40 44 48 5 4 12 13 61 31 14 33 53 15 49 11 26 33
14 13 55 11 50 14 34 9 46 35 52 41 54 20 11 15 45
22 11 60 52 45 53 21 44 10 59 23 4 45 43 7 2 36
32 40 28 50 42 50 44 20 1 12 3 24 59 33 62 31 21
37 52 1 55 30 20 13 14 39 15 50 6 31 11 25 11 5
12 16 27 21 34 49 48 13 44 44 8 6 58 41 28 29 29

It seems as though the 340 behaves more like your matrix than route transposition, Jarlve.

It seems as though the 340 behaves more like your matrix than route transposition, Jarlve.

Yes, my point exactly and thanks for confirming.

So what I am trying to get at is that with periodic transposition we may have been over assumptious with the order the plines are in. To give a crude and extreme example, here follows a cipher with the plaintext of the 408 where the row order has been randomized in a 5 by 68 configuration. Bigrams are high but the solution is junk with an AZdecrypt score of 20780.

KM!O"6WS'Y;-(:=$<
]%A1,8Z@LH;K<?W-;
F9/1DPYV]K]58N3&
(0C=M2%4SCR/)7JW
=AV$^E]AH!683I*]_
CG2D5F&8ZJY-(+/1
^4];-/[>)DEK:MA-;
Z#Y-P=BO,]7C(<8L2
.">A@=/TQU;]X86W!
#&H/*$NFJ]?)Z7Y4E
'(-;AZ!YEFI_^V65;
7&81,/9]0PK-;OD_G
S(B,IM8.^:!9O5@A/
Z>Y-*2H7[M5]4!;-N
)F/0(P($SC/M7J1:C
]A!YE;985/]<8@XI%
(-;-;FML9/B7R"DNA
!]!FZ0Y-;98/E(#AZ
<]H_SQK5KO47!68!F
/M]F&8,Z_W-2G)^>Y

Looking at the 17 by 20 configuration of the 340, with a transposition reading rule of "go left by 2 and go down by 1" (period 19 bigram peak) then there are whopping 55 plines/fragments that can be out of order. While with a regular period 19 transposition there are only 18 plines/fragments to consider.

I am trying to formulate some attack plan, possibly a hill climber.

I understand what you are saying about 55 plines ( parallel lines ). We worked on that a long time ago. You made a picture showing the start points of the 55 plines, and asked me to make a message. You were able to recover a few contextual words from the plaintext, I was impressed, you didn’t seem impressed, then we moved on to something else.

I am glad that we covered so much territory, but only at minimal depth in a lot of areas. It is funny, I find myself returning to ideas previously worked on.

Are you thinking about hill climbing a reorganization of the plines? What about the idea where either a special symbol or the end of a row tells the program to look up scores for 1 grams, then 2 grams, then 3 grams, etc. moving away from the special symbol or end of row. Like at the end of the message. The program has a one dimensional array 0-339 that holds the message, and another array 0-339 that holds the scores? What about another array in between where each cell holds a value that designates what n gram table to look up the score in. Find some versatile way to use that, maybe that would have more uses than hill climbing a reorganization of fragments. But I don’t know exactly what you do…

The scrolling test was with only two messages. If you want, I could perform more thorough scrolling / similar experiments and delve into your transposition scheme a little more before you do anything. Let me know.

I am still working on the 340 over here a little bit at a time. Sometimes I don’t know what to do. It is very hard.

I tried a simple multiple transcription idea, something that I have been thinking about for quite a while. Two 17 x 10 transcription rectangles, top half and bottom half, vertical transcription, periods 19 and 21. Expanded the + and tried all untransposed possibilities. No solve.

I understand what you are saying about 55 plines ( parallel lines ). We worked on that a long time ago. You made a picture showing the start points of the 55 plines, and asked me to make a message. You were able to recover a few contextual words from the plaintext, I was impressed, you didn’t seem impressed, then we moved on to something else.

Yes, I remember.

I am glad that we covered so much territory, but only at minimal depth in a lot of areas. It is funny, I find myself returning to ideas previously worked on.

Indeed.

Are you thinking about hill climbing a reorganization of the plines?

Yes.

What about the idea where either a special symbol or the end of a row tells the program to look up scores for 1 grams, then 2 grams, then 3 grams, etc.

It is on my to do list, I briefly looked at it and it will require some optimization and thought.

I decided to merge the pline rearrangement with my transposition solver (somehow).

My current thoughts are that the correlation between the 340 and the magic square reading rule is significant. And the period operation we have been using (columnar transposition) is not very able to get a solve on different pline orders.

A few questions,

Would any kind of misalignment within a pline order such as the magic square reading rule (go 2 squares left and 1 up) be more likely to cause a period shift from 38 to 39, or 30 to 29? In other words, is the periodic bigram peak at 39 caused by the pivots or has the period shift caused the pivots. The chicken or the egg.

And would any random pline order create a bigram peak at period column 2 such as the 340 and the magic square reading rule inspired matrix that I made? Or is it only that periodic pline orders cause these?

Those are some good questions. Let’s say I write the message at an angle, over two down one. When I get to column 17 and want to continue to the left side of the message, I move 19 spaces, which skips row 10 ( top picture ). That’s period 19 transposition and creates no misalignments.

Here is you matrix ( middle picture ). If I go right two spaces, but stay in row 9, then down one, I really only move two spaces. Period 2 becomes period 21, and period 3 becomes period 40. So that seems to make the matrix less viable.

But what if I start a new parallel line on row ten ( bottom )? . Period 1 becomes period 1, period 2 becomes period 20, and period 3 would become period 39. Maybe the pivots were created by some type of improper diagonal transposition, but the message was re-drafted into a different shape thus putting the pivots in the center of the message.

The only thing is, there are fewer period 3 repeats to work with even before homophonic diffusion.

What about the idea where either a special symbol or the end of a row tells the program to look up scores for 1 grams, then 2 grams, then 3 grams, etc.

It is in the works. The row solver currently uses 3,4,5 and 6-grams. The smaller ngram sizes are used to capture the information at the end of each row.

So I tried it on a 340 character piece of the 408 with a period 19 transposition and then extracted the 55 plines. It solved but the balance is very tedious with 55 plines.

solution:

Adjusted multiplicity: 0.28219
Score: 16671.52 Ioc: 0.06533

E
F
NK
TH
MAN
TUE
ILLS
ETHE
EXPER
ETTER
OURROC
RLTHEB
IATHAEW
LBEREBO
CEANDALL
LLEDWILL
LAVESIWIL
OUMYNAME
OUWILLTRY
INGPEOPL
TISSOMUCH
REFUNTHA
ILDGAMEIN
TBECAUSE
OATDANGER
OFALLTOK
INGGIVESM
HRILLING
ITISEVENB
GETTINGY
FFWITHAGI
PARTOFIT
NIDIEIWIL
INPARADI
HEIHAVEKI
ECOMEMYS
LNOTGIVEY
BECAUSEY
ILIKEKILL
BECAUSEI
UNITIAMO
ILLINGW
EFORRES
ISTHEM
ANAMAL
OMETH
MOATT
ENCE
THAN
KSO
EST
HE
RN
T
B

cipher:

W
J
(/
LM
qGD
IYE
P#B@
pI)W
+j=6
WI5+t
TYrde
t%L)NV
98LMlNA
BVW+VT
e67DzG%%
%%ZfAP#B
#8c+@9A9B
dYq_^SqW
TYA9%#Lt_
kOR=pX=B
HP@K!qYeM
tNQYD5)S
U%fRlqEk^
HVWe8Y@+
X85zS(RNt
TQS#BLd/
U^RRkcZKq
Mr9#BPDR
UHkFZcpOV
R6HI9DR_
JQAP5M8RU
=GrI!Jk5
(PzUpkA9#
P^=SrlfU
MNk)ScE/9
peXqWq_F
%OT5RUc+_
VZeGYKE_
9%P/Z/UB%
V+eGYF69
Y^UIk7qT
9#BPORA
ZJdrpF
9KI)6q
lO8qGB
XqEHM
q!85L
N(eE
L)l^
/@X
EKH
)Z
tO
I
V

I just checked p15 and 19 for the 340 and the best result came from p15 but does not seem to be a solve comparing it to 16671 score of the 408 piece. Double checking the solution would not be a bad idea though. Anyway, this row solver was a really great idea smokie. I am sure that it will be useful in many ways, do you want to be credited in any way?

solution:

Adjusted multiplicity: 0.32923
Score: 14863.03 Ioc: 0.05941

F
U
ID
BC
DMH
VAH
OPYU
ODFM
LADSW
IRDTO
OWITHI
OWRAYW
NAINTUO
EFILLED
SIMISSYK
NETAGODD
HTTOOLINM
NEOFFITH
EWOMANYPE
RAREEACR
ENYAMEREA
NTOUSESM
LTSSTEPTS
KOWASABE
SSOFUNNYS
OMMSANTO
NTCITEDST
GHTHATIT
FUNOWHERT
ITTOBEHE
ITINGSIGU
PMRAGEII
FOGOODMOD
YWHENITD
ESSTHECON
TOFUNDED
MERGLORIE
PLCKNOWL
UKOHASBET
PEWITHAS
YSAMPLEM
IVELAAO
ONYPLAC
ELVESO
RDDREA
ETYRI
OBLAY
ERPL
SDRO
TFN
TOE
SH
OW
T
E

cipher:

d
2
G)
Tf
LKJ
1*H
|<z2
k.#K
PYLR/
VW)+k
^D(+4(
l%WO&D
pOGp+2|
>#Z3P>L
R(UVFFz9
EB+*5k.L
H+M8|CV@K
pclddG+4
N:^j*Xz6-
y7t-cYAy
BpzOUNyBO
p+l2_cFK
SMF;+B<MF
9^%OF7TB
_Rq#2pb&R
8KjROp+8
p+fZ+B.;+
5J+JYM(+
#2b^D4ct+
G++|TB4-
(MVE5FV52
<Ut*5cZG
dl5||.UqL
z/JNbVM)
-RR+4>f|p
+l#2E.B)
Ucy5C^W(c
<Sf9pl/C
29^4OFT-+
6N:(+H*;
zF*K<SBK
G1BCOO|
lXz6PYA
B31c_8
y.LWBO
c+ztZ
|TC7z
cW<S
R)Wk
+dp
+kN
FH
|D
M
>

This is really great, Jarlve. I am so happy that you did that. Even though the solve above isn’t perfect, it is still a pretty good solve. You can read a lot of it. I say when you are ready we test it on various different types of transpositions, a variety of messages, plines and transpositions with various disturbances. Compare with untranspositions and the regular solver, solve independent chunks of messages. Before attacking the 340. Thanks.

We work together. I want to solve the 340, have a few beers together and high five. If not, then move on to retirement or semi retirement in peace. You can credit me with the idea if you want to.

Here is smokie39 again. Inscription rectangle 34 columns x 10 rows LRTB, reading TBLR making it period 10, transcription is LRTB into a 17 x 20, except that rows 3 and 18 are transcribed RL. The 7 symbol is a polyphone. You should be able to expand the 7, then untranspose rows 4-17 at period 10, use the row solver and get a solve.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
12 18 19 20 15 21 22 23 24 25 1 26 27 10 17 28 25
29 7 30 4 31 32 33 34 35 20 36 13 20 37 38 39 6
40 2 27 41 12 7 11 5 12 33 9 14 41 42 43 40 25
23 15 8 44 45 41 36 16 40 46 47 48 49 1 4 17 18
24 19 50 21 51 7 52 37 28 6 44 27 34 53 54 41 20
33 55 54 7 50 7 14 13 38 2 7 56 53 9 23 57 58
35 5 52 30 59 39 8 60 20 24 2 42 7 61 11 14 48
21 2 40 7 11 44 15 27 23 2 28 32 29 53 38 49 16
37 31 7 39 44 14 54 28 6 25 13 37 55 15 14 18 32
19 41 57 56 8 62 7 26 27 10 37 49 32 33 35 40 7
7 12 24 27 6 63 20 47 14 57 49 25 30 2 3 6 38
48 35 27 7 15 43 53 13 37 49 25 15 23 37 16 32 42
38 34 7 45 20 63 52 53 58 25 54 4 30 55 42 56 16
59 28 60 61 17 7 21 7 3 20 42 35 7 26 6 12 5
61 9 14 7 8 24 20 51 43 19 4 30 4 25 27 39 63
63 15 15 36 56 21 62 34 55 14 16 42 35 7 18 20 7
44 50 28 25 15 40 41 30 2 38 5 1 38 21 34 7 37
44 32 55 19 41 36 7 57 59 41 11 56 14 20 60 62 32
7 22 27 25 3 23 61 36 28 43 43 1 30 60 40 61 38