Are you shuffling symbols at regular intervals to find out if there is an increase in cycle scores, trying to find perhaps a part of the message that is not encoded as part of the cycles? I don’t quite understand what offset 21 means.
Yes, it struck me that I had not done this analysis before. It doesn’t make sense in a horizontal encoding hypothesis but you never know. I still need to compare the results to many other ciphers to get a feel for it. Offset is just the column number minus one, if you for example format the 340 in 19 columns than offset 18 is the last column.
Okay,
I am trying to see if more information about the supposed distribution of encoding randomness in the 340 can be gathered. With that in mind I compared the 340 versus two hypotheses.
Hypothesis 1: encode plaintext with homophonic substitution and perfect cycles with a raw ioc of 2236 and 34 character randomizations as last step also matching the 2-symbol cycle score of the 340.
Hypothesis 2: encode plaintext with homophonic substitution and randomized cycles to match the 2-symbol cycle score of the 340 with a raw ioc of 2236.
In both cases the distribution of the encoding randomization is spread out (or is expected to) throughout the cipher. Findings are that these hypotheses do not match the 340 very well. Randomization in symbols, rows and columns are not much present at all in comparison to the 340. Because in both hypotheses the encoding randomization is spread out through the cipher and therefore not local to any smaller unit of the cipher.
It could then be concluded that the supposed encoding randomization in the 340 is more local to symbols and/or rows, or yet unidentified units.
Hypothesis 1 cipher and results: 1 37 47 60 55 3 40 38 62 59 61 28 7 4 51 30 2 46 36 55 29 11 12 54 4 1 26 47 33 54 8 53 5 48 52 31 12 5 52 56 59 13 15 51 18 28 40 12 57 58 25 27 61 43 1 34 37 47 5 39 19 52 38 63 41 44 32 1 59 57 14 16 4 17 4 42 18 46 54 26 56 55 10 11 12 51 33 49 46 61 1 54 25 25 46 53 51 13 58 58 44 5 6 55 42 8 12 54 11 57 47 15 27 62 16 31 44 2 49 14 8 60 52 37 38 13 51 32 4 26 16 59 61 24 16 1 35 46 54 49 55 56 25 4 53 52 13 58 14 16 18 47 62 2 52 5 39 46 22 7 55 46 4 57 29 46 59 26 1 46 55 21 4 61 50 46 56 58 55 18 14 28 11 5 41 4 26 55 47 57 6 23 51 12 42 18 8 48 3 13 51 40 17 19 38 58 16 27 24 59 42 34 14 25 46 52 55 54 26 30 44 18 56 8 31 1 58 47 13 14 16 11 26 19 25 4 61 52 33 59 46 1 19 22 37 38 13 55 42 4 26 51 18 5 52 57 7 55 42 44 63 59 10 46 11 61 20 27 62 2 6 16 55 1 25 46 35 4 43 47 34 37 46 33 19 52 38 62 50 55 29 8 15 46 32 23 54 2 11 21 46 13 59 19 1 34 37 5 51 58 28 59 55 55 23 8 12 49 23 20 27 53 4 9 46 48 44 12 54 55 23 51 12 19 52 38 62 53 18 23 AZdecrypt find encoding nulls stats for: p1.txt ---------------------------------------------------- Symbol randomizations using 2-symbol cycles weight=5: ---------------------------------------------------- 36: 35% (1) 9: 32% (1) 23: 16.8% (6) 20: 7.7% (2) 46: 3.7% (18) 12: 3.5% (9) 60: 2.9% (2) 55: 2.7% (17) 19: 2.2% (7) 49: 1.3% (4) 4: 1.2% (13) 42: 1.2% (6) 24: 0.89% (2) 50: 0.8% (2) 30: 0.70% (2) 53: 0.70% (5) 39: 0.70% (2) 16: 0.70% (8) 22: 0.70% (2) 3: 0.6% (2) 51: 0.6% (10) 54: 0.5% (9) 52: 0.5% (11) 44: 0.5% (6) 14: 0.5% (6) 21: 0.5% (2) 58: 0.4% (8) 40: 0.3% (3) 62: 0.3% (6) 18: 0.3% (8) 34: 0.3% (4) 35: 0.3% (2) 2: 0.2% (5) 26: 0.2% (8) 33: 0.2% (4) 8: 0.2% (7) 56: 0.2% (5) 43: 0.2% (2) 41: 0.2% (2) 1: 0.1% (11) 47: 0.1% (8) 59: 0.1% (10) 11: 0.1% (7) 31: 0.1% (3) 15: 0.1% (3) 25: 0.1% (7) 32: 0.1% (3) 17: 0.1% (2) 6: 0.1% (3) 37: 0% (6) 38: 0% (7) 61: 0% (7) 28: 0% (4) 7: 0% (3) 29: 0% (3) 5: 0% (8) 48: 0% (3) 13: 0% (8) 57: 0% (6) 27: 0% (5) 63: 0% (2) 10: 0% (2) -------------------- Average: 1.99% Row randomizations using 2-symbol cycles weight=5: ---------------------------------------------------- Row 1: 0% Row 2: 0% Row 3: 0.3% Row 4: 0% Row 5: 0% Row 6: 4.6% Row 7: 0% Row 8: 0% Row 9: 0.8% Row 10: 0.2% Row 11: 0% Row 12: 0% Row 13: 0% Row 14: 2.4% Row 15: 0.6% Row 16: 0% Row 17: 0.2% Row 18: 0.1% Row 19: 5% Row 20: 21.3% -------------------- Average: 1.77% Column randomizations impr. ratios using 2-symbol cycles weight=5: ---------------------------------------------------- Column 1: 0% Column 2: 0% Column 3: 0% Column 4: 0% Column 5: 0% Column 6: 0% Column 7: 0.4% Column 8: 0% Column 9: 0.2% Column 10: 0.3% Column 11: 0% Column 12: 0% Column 13: 0% Column 14: 0% Column 15: 0% Column 16: 0% Column 17: 0% -------------------- Average: 0.05% Periodic randomizations versus 2-symbol cycles weight=5: ---------------------------------------------------- Period 2: - Offset 0: 0% - Offset 1: 0% Period 3: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% Period 4: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% Period 5: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% - Offset 4: 0% Period 6: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% - Offset 4: 0% - Offset 5: 0% Period 7: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% - Offset 4: 0% - Offset 5: 0% - Offset 6: 0% Period 8: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% - Offset 4: 0% - Offset 5: 0% - Offset 6: 0% - Offset 7: 0% Period 9: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% - Offset 4: 0% - Offset 5: 0% - Offset 6: 0% - Offset 7: 0% - Offset 8: 0% Period 10: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% - Offset 4: 0% - Offset 5: 0% - Offset 6: 0% - Offset 7: 0.1% - Offset 8: 0% - Offset 9: 0% Period 11: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% - Offset 4: 0% - Offset 5: 0% - Offset 6: 0% - Offset 7: 0% - Offset 8: 0% - Offset 9: 0% - Offset 10: 0% Period 12: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% - Offset 4: 0% - Offset 5: 0% - Offset 6: 0% - Offset 7: 0% - Offset 8: 0% - Offset 9: 0.1% - Offset 10: 0% - Offset 11: 0% Period 13: - Offset 0: 0% - Offset 1: 0.2% - Offset 2: 0% - Offset 3: 0% - Offset 4: 0% - Offset 5: 0% - Offset 6: 0% - Offset 7: 0% - Offset 8: 0% - Offset 9: 0% - Offset 10: 0% - Offset 11: 0% - Offset 12: 0% Period 14: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% - Offset 4: 0.1% - Offset 5: 0% - Offset 6: 0% - Offset 7: 0% - Offset 8: 0.1% - Offset 9: 0.3% - Offset 10: 0% - Offset 11: 0% - Offset 12: 0% - Offset 13: 0% Period 15: - Offset 0: 0.1% - Offset 1: 0% - Offset 2: 0.8% - Offset 3: 0% - Offset 4: 0% - Offset 5: 0% - Offset 6: 0% - Offset 7: 0% - Offset 8: 0% - Offset 9: 0% - Offset 10: 0.2% - Offset 11: 0% - Offset 12: 0.1% - Offset 13: 0% - Offset 14: 0% Period 16: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0.2% - Offset 3: 0% - Offset 4: 0% - Offset 5: 0% - Offset 6: 0% - Offset 7: 0% - Offset 8: 0% - Offset 9: 0% - Offset 10: 0% - Offset 11: 0% - Offset 12: 0% - Offset 13: 0.89% - Offset 14: 0% - Offset 15: 0% Period 17: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% - Offset 4: 0% - Offset 5: 0% - Offset 6: 0.3% - Offset 7: 0% - Offset 8: 0.1% - Offset 9: 0.5% - Offset 10: 0% - Offset 11: 0% - Offset 12: 0% - Offset 13: 0.1% - Offset 14: 0% - Offset 15: 0% - Offset 16: 0% Hypothesis 2 cipher and results: 53 44 1 3 56 62 38 54 54 45 29 6 7 4 8 57 54 46 50 55 10 60 12 41 56 48 42 53 58 41 8 15 12 10 30 17 12 51 1 43 38 58 31 8 36 4 24 12 5 49 16 11 51 3 53 2 44 1 5 6 28 38 44 34 32 47 15 46 45 29 61 30 55 17 8 37 39 56 13 61 63 4 10 60 12 41 46 31 11 51 48 58 14 30 55 31 8 41 42 40 47 5 59 56 18 8 12 58 11 29 53 15 47 54 8 24 60 2 44 43 8 62 1 54 2 13 8 31 4 42 16 38 51 6 32 45 21 46 41 15 55 43 30 46 31 8 58 49 61 16 36 48 44 54 53 5 59 55 22 7 56 37 4 29 10 46 1 49 38 13 55 52 56 51 9 4 61 42 46 39 43 30 11 5 6 55 49 61 45 29 32 35 8 12 18 36 8 10 3 41 8 17 24 26 48 14 16 47 59 45 37 2 42 30 56 25 4 58 43 57 60 39 49 8 17 53 61 48 13 14 30 47 49 28 16 46 51 53 20 1 55 38 19 45 44 54 50 4 37 46 63 8 39 5 48 29 7 60 18 11 33 53 10 55 47 51 34 60 54 2 61 30 56 1 16 11 21 4 62 53 2 54 46 40 26 1 2 54 50 55 10 8 15 56 15 23 41 2 47 52 46 58 38 19 45 44 54 5 8 43 32 48 21 55 27 8 12 15 35 29 60 31 55 63 56 10 11 12 13 4 23 8 12 26 53 2 54 49 36 27 AZdecrypt find encoding nulls stats for: p1.txt ---------------------------------------------------- Symbol randomizations using 2-symbol cycles weight=5: ---------------------------------------------------- 9: 38.9% (1) 25: 31% (1) 33: 28.9% (1) 20: 28.1% (1) 22: 26.2% (1) 27: 19.2% (2) 23: 14.4% (2) 19: 6.1% (2) 54: 5.9% (12) 8: 4.9% (19) 26: 3.9% (3) 12: 3.8% (10) 21: 3.8% (3) 31: 3.2% (6) 57: 3.1% (2) 15: 2.6% (7) 40: 2.6% (2) 50: 2.5% (3) 35: 2.4% (2) 3: 2.3% (3) 34: 2.3% (2) 2: 2.2% (9) 17: 1.9% (4) 52: 1.6% (2) 49: 1.3% (7) 28: 1.2% (2) 60: 1.1% (7) 7: 1% (3) 18: 1% (3) 14: 0.89% (3) 61: 0.8% (7) 53: 0.6% (10) 62: 0.6% (3) 6: 0.6% (4) 42: 0.6% (5) 39: 0.5% (4) 55: 0.4% (12) 41: 0.4% (7) 58: 0.4% (7) 47: 0.4% (7) 59: 0.4% (3) 44: 0.3% (7) 1: 0.3% (8) 46: 0.3% (11) 24: 0.3% (3) 10: 0.2% (8) 30: 0.2% (8) 36: 0.2% (4) 11: 0.2% (7) 63: 0.2% (3) 56: 0.1% (10) 43: 0.1% (6) 16: 0.1% (6) 32: 0.1% (4) 37: 0.1% (4) 13: 0.1% (5) 38: 0% (7) 45: 0% (7) 29: 0% (7) 4: 0% (10) 48: 0% (7) 51: 0% (7) 5: 0% (7) -------------------- Average: 4.07% Row randomizations using 2-symbol cycles weight=5: ---------------------------------------------------- Row 1: 1% Row 2: 0.8% Row 3: 1.2% Row 4: 0% Row 5: 0% Row 6: 1.9% Row 7: 0.70% Row 8: 0.1% Row 9: 0.4% Row 10: 0.2% Row 11: 0.6% Row 12: 0% Row 13: 0% Row 14: 3.1% Row 15: 0% Row 16: 0.4% Row 17: 5.5% Row 18: 0.89% Row 19: 0% Row 20: 1.4% -------------------- Average: 0.90% Column randomizations impr. ratios using 2-symbol cycles weight=5: ---------------------------------------------------- Column 1: 0% Column 2: 0.2% Column 3: 0% Column 4: 0% Column 5: 0% Column 6: 0.4% Column 7: 0% Column 8: 0% Column 9: 0% Column 10: 0% Column 11: 0% Column 12: 0.5% Column 13: 0% Column 14: 0% Column 15: 0% Column 16: 0% Column 17: 0% -------------------- Average: 0.06% Periodic randomizations versus 2-symbol cycles weight=5: ---------------------------------------------------- Period 2: - Offset 0: 0% - Offset 1: 0% Period 3: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% Period 4: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% Period 5: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0.1% - Offset 3: 0% - Offset 4: 0% Period 6: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% - Offset 4: 0% - Offset 5: 0% Period 7: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% - Offset 4: 0% - Offset 5: 0% - Offset 6: 0% Period 8: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% - Offset 4: 0.1% - Offset 5: 0% - Offset 6: 0% - Offset 7: 0% Period 9: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% - Offset 4: 0% - Offset 5: 0% - Offset 6: 0% - Offset 7: 0% - Offset 8: 0% Period 10: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% - Offset 4: 0% - Offset 5: 0% - Offset 6: 0% - Offset 7: 5% - Offset 8: 0% - Offset 9: 0% Period 11: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% - Offset 4: 0% - Offset 5: 0% - Offset 6: 0% - Offset 7: 0% - Offset 8: 0% - Offset 9: 0% - Offset 10: 0% Period 12: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% - Offset 4: 0% - Offset 5: 0% - Offset 6: 0% - Offset 7: 0% - Offset 8: 0% - Offset 9: 0.4% - Offset 10: 0% - Offset 11: 0% Period 13: - Offset 0: 0% - Offset 1: 2.3% - Offset 2: 0% - Offset 3: 0% - Offset 4: 0% - Offset 5: 0% - Offset 6: 0% - Offset 7: 0% - Offset 8: 0% - Offset 9: 0% - Offset 10: 0% - Offset 11: 0% - Offset 12: 0% Period 14: - Offset 0: 1.2% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% - Offset 4: 0% - Offset 5: 0% - Offset 6: 0% - Offset 7: 0% - Offset 8: 0% - Offset 9: 0% - Offset 10: 0% - Offset 11: 0.1% - Offset 12: 0% - Offset 13: 0.4% Period 15: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0.3% - Offset 3: 0% - Offset 4: 0% - Offset 5: 0% - Offset 6: 0% - Offset 7: 0.1% - Offset 8: 0% - Offset 9: 0% - Offset 10: 0% - Offset 11: 0% - Offset 12: 2.1% - Offset 13: 0.1% - Offset 14: 0% Period 16: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% - Offset 4: 0.1% - Offset 5: 0.3% - Offset 6: 0% - Offset 7: 0% - Offset 8: 0% - Offset 9: 0% - Offset 10: 0% - Offset 11: 0% - Offset 12: 0% - Offset 13: 0.70% - Offset 14: 0% - Offset 15: 0% Period 17: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% - Offset 4: 0% - Offset 5: 0.4% - Offset 6: 0.1% - Offset 7: 0% - Offset 8: 0% - Offset 9: 0.2% - Offset 10: 0% - Offset 11: 0.1% - Offset 12: 0% - Offset 13: 0% - Offset 14: 0% - Offset 15: 0% - Offset 16: 0%
Results for the 340 are a few posts up.
Your work sounds exciting. I see, because an array starts with position 0, if you drafted the message into 35 columns, then offset 21 means shuffling the 22nd column.
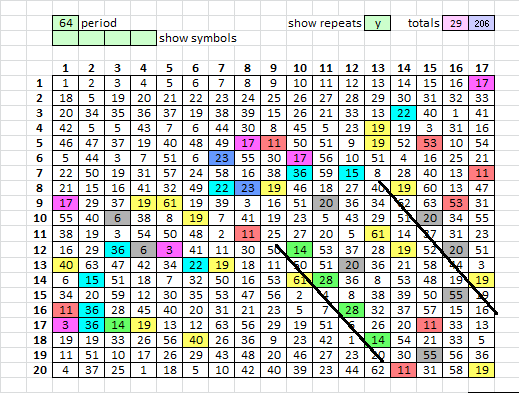
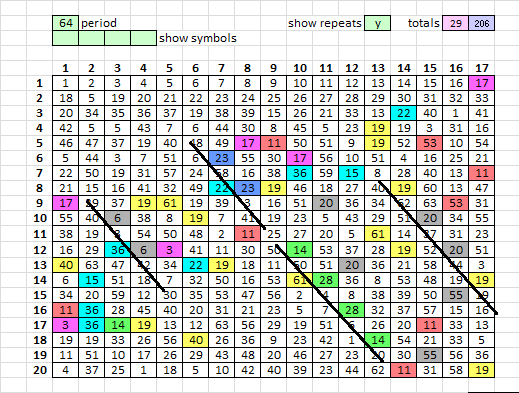
These symbols appear as part of the highly improbable period 64 bigram repeats ( score wise the least probable of all periods ), right? Symbols 14-28-28-14. Note also that they form parts of two interesting rotated box patterns. They also appear as part of the herringbone pattern in recent post above.
A while ago I was trying to replicate the strange P19LRTB-P16RLBT herringbone pattern. Here is the idea. Draft two separate messages, or two parts of the same message, into two transcription rectangles. Below light blue transcription is TBLR and light yellow diagonal RLBT. Then separate the columns into a pattern and splice the two messages together. I just checked it for bigrams to see if I could make the herringbone and I could sometimes, but not quite as good as the 340.
I didn’t think to examine the idea for cycles. Perhaps encoded with the symbols, and then spliced. Something like that.
Here are the symbols that I think you are talking about, marked in yellow and red, red as parts of the three strange rotated boxes.
Yes, the symbols in red and yellow exactly. What do you mean with rotated boxes?
Your work sounds exciting. I see, because an array starts with position 0, if you drafted the message into 35 columns, then offset 21 means shuffling the 22nd column.
Sometimes I start them at 0, other times at 1, I personally prefer counting from 1. I will rename offset to column and +1 it to not confuse people. The fragments/units (in this case columns) are not shuffled, for each position a random symbol is chosen from the original cipher itself. This will make it follow the frequency distribution of the cipher. Shuffling a unit, like a row, would not change so much since the order of the cycles is still largely preserved.
I am not sure about your transcription rectangle idea and would not like to go on a tangent right now.
No tangent intended.
Rotated boxes, see the red and green 45 degree period 64 boxes, and red and blue 45 degree period 64 boxes above.
Of all periods, the period 64 repeats are the least probable when taking into consideration the count of all of the symbols involved.
I am trying to see if more information about the supposed distribution of encoding randomness in the 340 can be gathered
Looking further. A polyphone could be any distribution of letters, and more generally we could consider a polyphone to be either a merged set of symbols (consuming all the instances of these symbols) or a merged set of random characters from throughout the cipher of any frequency.
Hypothesis 1: encode plaintext with homophonic substitution and perfect cycles and then merge sets of symbols into polyphones.
Hypothesis 2: encode plaintext with homophonic substitution and perfect cycles and then merge random characters into polyphones.
No more than about 20% randomization in rows was seen (remember that the 340 has row 14 with nearly 70%). Randomization in columns more or less was comparable with the 340. There was more sign of randomization in the polyphone symbols with hypothesis 2 than hypothesis 1. Hypothesis 1 does barely randomize perfect cycles, hypothesis 2 is better in that regard. I feel that both of these hypothesis are not a good match for the 340 and can at best be only partially true.
Hypothesis 3: encode plaintext with homophonic substitution and perfect cycles and randomize the positions of one row.
Hypothesis 4: encode plaintext with homophonic substitution and perfect cycles and replace one row with random filler.
Randomization in the affected row for hypothesis 3 was generally low, anywhere from 5% to 20%. Hypothesis 4 matched the randomization seen in row 14 of the 340 very well with anywhere from 40% to 70%. Both hypotheses on their own are however not enough to disturb the encoding to the extent of the 340.
It seems likely that in the 340, row 14 or a large part thereof is random filler or consisent with such. Looking at rows in the 340 in 34 by 10 (smaller units), it can be seen that almost all of the randomization seems to take place from row 16 and onwards, the second part of the cipher. Both pivot sections are highly involved, thus it seems highly likely that the pivots were artificially created by the author.
340 results 34 by 10:
AZdecrypt find encoding nulls stats for: 340.txt ---------------------------------------------------- Symbol randomizations using sequential: ---------------------------------------------------- +: 85.2% (24) <-- may be a polyphone ): 25.83% (5) p: 24.76% (11) W: 19.31% (6) B: 16.74% (12) F: 16.19% (10) .: 12% (6) 4: 9.48% (6) G: 7.96% (6) 2: 7.07% (9) k: 3.8% (5) L: 3.23% (6) T: 3.19% (5) M: 2.57% (7) R: 1.24% (8) O: 0.63% (10) (: 0.37% (7) z: 0.36% (9) |: 0.35% (10) c: 0.19% (10) H: 0% (4) E: 0% (3) >: 0% (4) l: 0% (7) ^: 0% (6) V: 0% (6) P: 0% (3) 1: 0% (3) d: 0% (5) N: 0% (5) #: 0% (5) %: 0% (2) D: 0% (4) Y: 0% (4) <: 0% (6) *: 0% (6) K: 0% (7) f: 0% (4) y: 0% (5) :: 0% (2) U: 0% (5) Z: 0% (4) J: 0% (4) S: 0% (4) 7: 0% (3) 8: 0% (4) 3: 0% (2) _: 0% (3) 9: 0% (4) t: 0% (4) j: 0% (2) 5: 0% (7) &: 0% (2) /: 0% (3) -: 0% (5) C: 0% (5) q: 0% (2) ;: 0% (3) X: 0% (2) @: 0% (1) b: 0% (3) A: 0% (2) 6: 0% (3) -------------------- Average: 3.81% Row randomizations using 2-symbol cycles weight=5: ---------------------------------------------------- Row 1: 0.5% Row 2: 0.4% Row 3: 0% Row 4: 0% Row 5: 1.6% Row 6: 4.4% Row 7: 1.5% Row 8: 0.5% Row 9: 1.9% Row 10: 6.4% Row 11: 0.2% Row 12: 3.9% Row 13: 0.4% Row 14: 2.3% Row 15: 0.70% Row 16: 12.9% Row 17: 29.9% Row 18: 0.1% Row 19: 36.8% Row 20: 45.3% <--- pivot 1 Row 21: 1.1% Row 22: 23% Row 23: 41.2% Row 24: 63.7% <--- pivot 2 Row 25: 0% Row 26: 1.3% Row 27: 0.1% Row 28: 4.8% Row 29: 21.5% Row 30: 39.2% Row 31: 2% Row 32: 0.3% Row 33: 2.8% Row 34: 3% -------------------- Average: 10.40% Column randomizations using 2-symbol cycles weight=5: ---------------------------------------------------- Column 1: 0% Column 2: 0.1% Column 3: 0% Column 4: 0.4% Column 5: 0.4% Column 6: 0% Column 7: 0.8% Column 8: 0% Column 9: 0% Column 10: 0% -------------------- Average: 0.17% Periodic randomizations versus 2-symbol cycles weight=5: ---------------------------------------------------- Period 2: - Offset 0: 0% - Offset 1: 0% Period 3: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% Period 4: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% Period 5: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% - Offset 4: 0% Period 6: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% - Offset 4: 0.1% - Offset 5: 0% Period 7: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% - Offset 4: 0% - Offset 5: 0% - Offset 6: 0% Period 8: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% - Offset 4: 0% - Offset 5: 0% - Offset 6: 0% - Offset 7: 0% Period 9: - Offset 0: 0% - Offset 1: 0% - Offset 2: 0% - Offset 3: 0% - Offset 4: 0.1% - Offset 5: 0% - Offset 6: 0% - Offset 7: 0% - Offset 8: 0.1% Period 10: - Offset 0: 0% - Offset 1: 0.2% - Offset 2: 0% - Offset 3: 0.2% - Offset 4: 0.4% - Offset 5: 0% - Offset 6: 0.5% - Offset 7: 0.1% - Offset 8: 0% - Offset 9: 0%
If row 14 is randomized somehow then I wonder how it would fit in with the cipher.
I checked the following options.
Good candidates:
– Randomize a row with random filler.
– Add row with random filler.
Bad candidates:
– Swap 2 rows.
– Randomize the positions of a row.
– Remove a row.
And now distinguish between the good candidates.
hi jarlve.. that`s hard for me to follow without visuals
so if by chance row 14 is filler how do we get row 14 to be the last line of the code or what is the encryption to do that?
cheers
hi jarlve.. that`s hard for me to follow without visuals
so if by chance row 14 is filler how do we get row 14 to be the last line of the code or what is the encryption to do that?
cheers
I am still trying to find out exactly what is wrong with row 14.
Some options to ponder:
– The row is random filler, such that it needs to be removed.
– Homophones were not cycled in this row.
– A large amount of polyphones in this row.
It is a good idea that the row might be out of order, as you suggest it may be the last line in some way.
Row 14 has some of the pivots symbols, and two of the + symbols.
Have you tried to randomize odds / evens?
Have you tried to randomize odds / evens?
Randomized odds:
Rows, randomize characters, using 2-symbol cycles weight=5: ---------------------------------------------------- Row 1: 3.15% Row 2: 0.1% Row 3: 0.65% Row 4: 14.4% Row 5: 0.1% Row 6: 27.8% Row 7: 0% Row 8: 3.85% Row 9: 0.5% Row 10: 11.95% Row 11: 9.25% Row 12: 13.15% Row 13: 24.1% Row 14: 59.75% <--- Row 15: 0% Row 16: 0.15% Row 17: 4.4% Row 18: 22.05% Row 19: 1.8% Row 20: 0.35% -------------------- Average: 9.87%
Randomized evens:
Rows, randomize characters, using 2-symbol cycles weight=5: ---------------------------------------------------- Row 1: 0% Row 2: 1.15% Row 3: 0.35% Row 4: 3.45% Row 5: 0.05% Row 6: 1.4% Row 7: 9.85% Row 8: 1% Row 9: 3.1% Row 10: 21.95% Row 11: 2.95% Row 12: 21.65% Row 13: 3.55% Row 14: 48.1% <--- Row 15: 0.2% Row 16: 3.55% Row 17: 17.9% Row 18: 10.45% Row 19: 0.65% Row 20: 8.6% -------------------- Average: 7.99%
Have you tried to randomize odds / evens?
Randomized odds:
Rows, randomize characters, using 2-symbol cycles weight=5: ---------------------------------------------------- Row 1: 3.15% Row 2: 0.1% Row 3: 0.65% [b]Row 4: 14.4%[/b] Row 5: 0.1% [b]Row 6: 27.8%[/b] Row 7: 0% Row 8: 3.85% Row 9: 0.5% [b]Row 10: 11.95%[/b] Row 11: 9.25% [b]Row 12: 13.15%[/b] Row 13: 24.1% [b]Row 14: 59.75% <---[/b] Row 15: 0% Row 16: 0.15%e Row 17: 4.4% [b]Row 18: 22.05%[/b] Row 19: 1.8% Row 20: 0.35% -------------------- Average: 9.87%
It seems like some of the even rows score higher here.
I started work on a cycle hill climber this morning named "Restore homophone cycles". Which will work just like any other solver module in AZdecrypt, though it uses perfect cycles as a measurement instead of ngrams. I am not sure yet how well this will work but it is an exciting project.
Here is a very early preview of it on the 408. Scroll down the code box until you see "Changes:", notice how it finds the distribution near the bottom (second half) of the cipher. Right now it seems to know where the randomness is but not exactly. From that information a heatmap could be built that hilights areas of probable encoding randomness. It may also tell us how well the 340 responds to this treatment.
Score: 22845.17 Ioc 1: 0.01829 Ioc 2: 0.88040
Pefect cycles: 85 Score: 13120
Match: 0.94852
9%P/Z(UB%kOR=pX=B
WV+eGYF69HP@K!qYe
MJY^UIk7qTtNQYD5)
S(/9#BPORAU%fRlqE
k^LMZJdrpFHVWe8Y
@+qGD9KI)6qX85zS(
RNtIYElO8qGBTQS#B
Ld/P#B@Xq=HMU^RRk
cZKqpI)Wq!85LMr9#
BPDR+z=6N(eEU/kF
ZcpOVWI5+tL)l^R6H
I9DR_TYrde/@XJQA
P5M8RUt%LSNVEKH=G
rI!Jk598LMlFA@Z(P
zUpkA9#BdW+VTtOP
^=SrlfUe67DzG%%IM
Nk)KcE/9%%ZfAP#B(
peXqHq_F#8c@9A9B
%OT5RUc+_dYq_^SqW
VNeGYKE_TYA9%#Lt_
HkFBl9zXAD)7L!=q
_ed##6e(PORXQF%/c
Z@JTtq_8JI+rBpQK6
V^Xr9WINqEHM)=UIk
Changes:
(
=
z /
S
F @
d
K (
H
N
k l )
( /
p K
^ N