Jarlve, please don’t think that I have stolen your idea! That the + symbols may result from a pattern prior transformation was an idea I had long time ago. I always thought that this high amount of + symbols dissents the character of homophonic substitutions.
But the diagonal + redraft idea may originally came because I read your post and then forget that I read it. In any case: If this approach leads to a solution the credit is definitely yours! I am not a person that steal ideas!

Jarlve, please don’t think that I have stolen your idea! That the + symbols may result from a pattern prior transformation was an idea I had long time ago. I always thought that this high amount of + symbols dissents the character of homophonic substitutions.
But the diagonal + redraft idea may originally came because I read your post and then forget that I read it. In any case: If this approach leads to a solution the credit is definitely yours! I am not a person that steal ideas!

I’m sorry, I didn’t ment to imply that at all. I’m happy that someone is generating the same ideas and you have a different take on it.

Experiment: Relationship between transposition scheme and cycle scores when message is encoded before transposition

I woke up this morning thinking about the possibility of encoding before transposition because of the above posts. I have tried it before, and found that, expectedly, encoding before transposition causes cycles to be destroyed. However, I was wondering about the 340 strange left right top bottom two symbol cycle score 64418. This is much more cyclic than the other directions but not nearly as cyclic as it would be if all perfect cycles or similar to the 408.

The question is: If I encode before transposition, can the size and shape of the inscription rectangle and inscription / transcription directions have much of an effect on cycle scores?

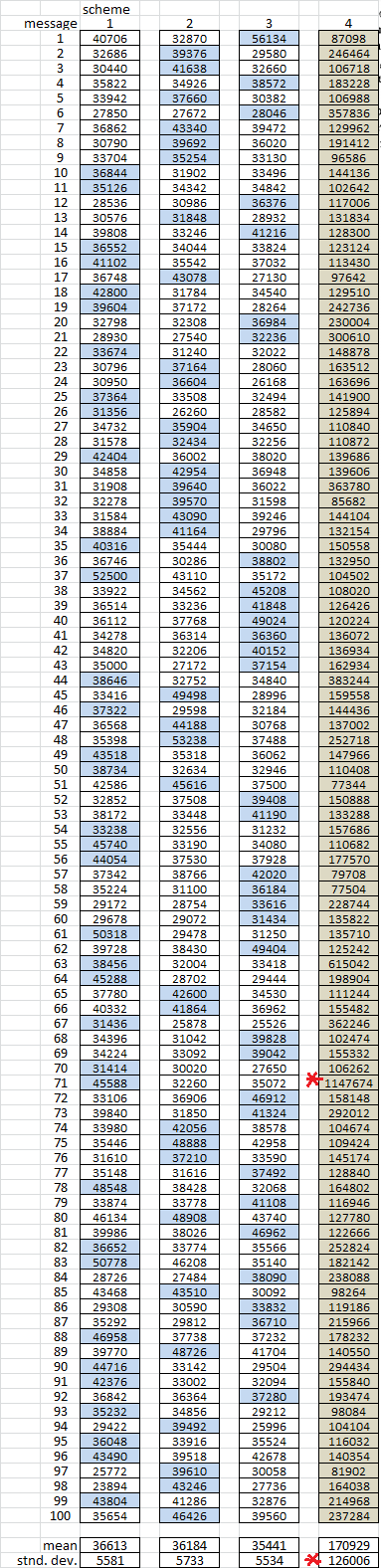
Below I tried four different schemes, three with big inscription and transcription rectangles, and one novelty transposition. All perfect cycles before transposition. The first three schemes resulted in low cycle scores, regardless of the shape of the inscription rectangle. But the novelty transposition cycle scores were actually much higher than 64418.

1. Scheme 1 has a 10 x 34 inscription rectangle, 17 x 20 transcription rectangle, and creates a lot of period 34 repeats.

2. Scheme 2 has 17 x 20 inscription and transcription rectangles, and creates a lot of period 20 repeats.

3. Scheme 3 has a 34 x 10 inscription rectangle, 17 x 20 transcription rectangle, and creates a lot of period 10 repeats.

I figured that maybe one would have higher cycles scores after transposition. I thought that maybe scheme 3 might have higher cycles scores, because it only makes period 10 repeats. The bigram plaintext is not spread very far apart, so the cycles may not be disrupted as much. A letter like R might appear several times in the plaintext, but if rearranged with a period 10 transposition, the cycle would not change very much.

4. The novelty transposition is a variation of something that I have been thinking about a lot these last several months. Period 1 becomes period N, and period 2 becomes period M, but unlike with the schemes 1 – 3, period M is not a multiplier of period N. The inscription rectangles are smaller, and probably too small to create as many period 15 / 19 repeats as with the 340. That is because there is no relationship between these small groups of symbols. However, it has a feature that I think is possible with the 340: alternating row or column inscription or transcription.

The novelty transposition uses 6 x 5 rectangles. Inscription is left right top bottom, but the symbols are lifted from the inscription rectangles vertically by alternating columns. Transcription is left right top bottom. EDIT: Period 1 becomes period 15, and period 2 becomes period 5.

5. Remember that the cryptography books discuss route transposition similar to below, where military cryptographers preferred small shapes to make transmission more reliable, untransposition faster and to eliminate the possibility of making mistakes which could cause misalignments.

6. First, I encoded all 100 of Jarlve’s plaintext message library with 99% perfect cycles. I used +/- 63 symbols for each message, and keys that are between highest and lowest possible efficiency. I did make one symbol a polyphone by mapping it to the three most frequent plaintext, to simulate the + symbol with count and cycle score.

7. Second, I transposed all 100 messages with the four schemes, and added up all of the two symbol cycle scores for each message and each scheme.

Results

Scheme 4 was far more cyclic than the other three schemes, and also far more cyclic than the 340. But first let’s compare schemes 1 – 3 without scheme 4.

Scheme 1 was more cyclic for 35 messages, had a mean cycle score of 36613 and a standard deviation of 5581.
Scheme 2 was more cyclic for 33 messages, had a mean cycle score of 36184 and a standard deviation of 5733.
Scheme 3 was more cyclic for 32 messages, had a mean cycle score of 35441 and a standard deviation of 5534.

Schemes 1 – 3 were all about the same. Expectedly none were very cyclic, but I was a little bit surprise that I could not distinguish any of them with the statistics. One big inscription and transcription rectangle, encoding before transposing, results in cycle scores lower than the 340.

Scheme 4 was much more cyclic than the 340, had a mean cycle score of 170929 and a standard deviation of 126006. ALL of the messages had scores higher than the 340, and the standard deviation is so high because some of the messages, like # 71, had extremely high scores.

Conclusion: Encoding one big inscription rectangle, then transposing into one big transcription rectangle, results in cycle scores lower than the 340. But, use of smaller inscription rectangles such as the novelty scheme, may result in cycle scores much higher than the 340.

Could the 340 have more than one inscription rectangle?

Hey smokie,

Nice work there. I believe there are few other things we have to take in consideration beside cycle scores.

Summing unigram repeats per row, the 340 comes in at 18, which is suprisingly low. It is so low that it does not occur even once in 1.000.000 million randomizations, the lowest found here is 22. Unigram repeats are very easily disturbed. Any periodical transposition will hugely increase them. Another thing which is very easily disturbed with transposition are the frequencies of unique sequence lengths, for the 340 they peak at 17 with 26 repeats. Just mirroring the cipher reduces that to a peak at 12 with 21 repeats. The unigram repeats themself rule out any periodical transposition after encoding. We need to look at transpositions which do not negatively affect these measurements.

And the encoding hypothesis I have put forward is really the most likely thing to have happened (do not repeat characters in a certain window, no intentional cycling). Why?

– The symbol frequency flatness of the 340 is proportional to the randomization in the encoding (frequency of the "+" symbol alone does not account for this change in flatness).
– Unigram repeats are extremely low.
– Peak unique sequence at length 17 with 26 repeats.

340:
Flatness: 0.6685691569412501
Row unigram repeats: 18
Length 17: 26

408: (340 character part)
Flatness: 0.854241338112306
Row unigram repeats: 21
Length 11: 20

Could the 340 have more than one inscription rectangle?

If you have a few of these ciphers lying around I would like to take a look at it.

And I have been thinking about running some variations of these through AZdecrypt but I would not know where to start. So, do you want to design such a test? I think you have the most experience with multiple rectangles. Then I’ll code it up and run it through AZdecrypt. We need to come up with some bounds though. I would prefer not to process more than 1.000.000 ciphers so that thorough settings can be used.

After running through 10.000.000 randomizations of the 340 measuring unigram per row repeats the lowest return is 20, while the 340 has only 18. It seems to be the most significant fact about the encoding. Such a low number generally disagrees with randomization of cycles unless the specific goal was to not repeat characters.

Combinations processed: 10000000/10000000
Measurements:
- Summed: 457286586
- Average: 45.7286586
- Lowest: 20 (Randomize(44005))
- Highest: 74 (Randomize(17505))

After running through 10.000.000 randomizations of the 340 measuring unigram per row repeats the lowest return is 20, while the 340 has only 18. It seems to be the most significant fact about the encoding. Such a low number generally disagrees with randomization of cycles unless the specific goal was to not repeat characters.

Very interesting… Regarding the unique sequence lengths peaking at 17 with 26 repeats: How does that peak compare to the randomizations? Is it unusual to have so many peaking at or near 17? Perhaps you already generated a comparison plot before and it’s buried somewhere in a thread.

After running through 10.000.000 randomizations of the 340 measuring unigram per row repeats the lowest return is 20, while the 340 has only 18. It seems to be the most significant fact about the encoding. Such a low number generally disagrees with randomization of cycles unless the specific goal was to not repeat characters.

Very interesting… Regarding the unique sequence lengths peaking at 17 with 26 repeats: How does that peak compare to the randomizations? Is it unusual to have so many peaking at or near 17? Perhaps you already generated a comparison plot before and it’s buried somewhere in a thread.

Hey doranchak,

Haven’t generated it before but here it is. It only returns a single number so I encoded it as "peak0repeats". So the highest here in 10.000.000 randomizations is peak 17 with 24 repeats, the 340 surpasses that. I actually did not realize it was this rare. Thanks for the suggestion.

Combinations processed: 10000000/10000000
Measurements:
- Summed: 71023361707
- Average: 7102.3361707
- Lowest: 2022 (Randomize(9933))
- Highest: 17024 (Randomize(53215))

I’m sorry, I didn’t ment to imply that at all. I’m happy that someone is generating the same ideas and you have a different take on it.

I was just afraid that you could think that I copied your work because my posting looked almost the same like yours. I am glad that everything is ok =)
Today I have read some threads about the prime phobia of the plus symbols in this forum. I found the thread http://zodiackillersite.com/viewtopic.php?f=81&t=2841 very interesting because of the explanations about the prime safe areas within an rectangle. As I read the thread I remembered an article about patterns in prime numbers. In this article a pattern named „Ulam Spiral“ was described. But this time I searched the forum for this term before posting anything about it. Guess what happened? You mentioned it a couple of months ago in the big thread about homophonic substitution. You had the same idea….again. And you were faster….again
If I will find some time I will posts some thoughts about this topic.

An interesting discussion of different ways to detect patterns in a grid: m http://stats.stackexchange.com/question … ary-matrix

Thank you for the link! I will put that onto my todo-list. At the moment I just have implemented a simple search for horizontal, vertical and diagonal plus patterns. It would be great to determine patterns in a more effective way.

But I highly recommend that you put your stuff up on github.

Thank you for sharing your code. I will definitively clone your repository and check its contents! I also use git for my projects so all I have to do is to push the repository to github (after cleaning up the code a bit)

Smokie:
Nice work and a lot of new aspects!

Personally I don’t think that Zodiac transposed an already enciphered text since this would mean that he had to draw all those symbols twice. I don’t know…but I think this guy was lazy (that’s only an assumption). The crossed out „k“ in z340 confirms that he was not willing to write the whole cipher again after he made a mistake (I would have started again since I am pedantic). Maybe he decided to make sure the symbols are not as cyclic as in z408 because z408 was broken because of the cycled symbols (repeating bigrams like double L).
When you are talking about schemes 1-4, what is scheme 4? In the image you posted there are only 3 schemes listed (A, B, and C).
Your idea that a couple of small inscription schemes could may have been used reminds me of some of my tests (Post from Jun 26, 5:13 am, section „Horizontal Stripes“):
http://zodiackillersite.com/viewtopic.php?f=81&t=3093

In this test I have cut the cipher into stripes and applied different transformations to each stripe before seaming them together again. (129056 permutations in total). Unfortunately „(B) Simple Vertical“ from your resource is not considered in my test. Maybe I will give it a try. I also created a similiar test for all permutations of quadrant sizes. In this post you will find a download link to the generated ciphers.
By the way: Do you remember my postings regarding to chunked transposition / chunk sizes? Basically a chunk based transposition is the same as a transposition with lots of very small inscription rectangles. Maybe you could check one of Jarlves test ciphers for cycles?
(http://zodiackillersite.com/viewtopic.php?f=81&t=3206&p=50662&hilit=chunk#p50662)

With all those possible transposition schemes in mind I ask myself very often if Zodiac wanted the cipher to be broken (I am not the only one I guess). In z408 he talked directly to the reader „I will not give you my name…“. So I think he did not try to be crackproof. Instead he knew that someone will break it. Same for z340? If so, I don’t think that he used a too complex enciphering method. In ’69 no one had a PC at home and I think that Zodiac did not expect that someone would detect a too complex transposition scheme. On the other hand….the cipher still remains unsolved. Errors in encipherment or a „brilliant“ homegrown idea which renders the cipher unsolvable seems more likely to me.

Summing unigram repeats per row, the 340 comes in at 18, which is suprisingly low. It is so low that it does not occur even once in 1.000.000 million randomizations, the lowest found here is 22. Unigram repeats are very easily disturbed. Any periodical transposition will hugely increase them. Another thing which is very easily disturbed with transposition are the frequencies of unique sequence lengths, for the 340 they peak at 17 with 26 repeats. Just mirroring the cipher reduces that to a peak at 12 with 21 repeats. The unigram repeats themself rule out any periodical transposition after encoding. We need to look at transpositions which do not negatively affect these measurements.

Sometimes it takes me a while to grasp a certain concept. You are saying that if you look at each row, then there are only 18 symbols repeated in the entire message, but if you shuffle the message that is not going to happen. I do not understand about the frequencies of unique sequence lengths peak at 17 with 26 repeats. And you are saying that if Zodiac encoded before transposing, then the same symbols would more frequently appear in the same rows as compared to the 340. I do understand that, and would like to test it.

And the encoding hypothesis I have put forward is really the most likely thing to have happened (do not repeat characters in a certain window, no intentional cycling). Why?

Why is the problem for me. If he did this intentionally, then what was he thinking? I do not see how this would make a homophonic substitution cryptogram more difficult to solve. Unless of course he was trying to avoid creating period 1 bigram repeats. But then we have the period 15 / 19 repeats. So I wonder if this is created by the cipher unintentionally instead of intentionally.

If you have a few of these ciphers lying around I would like to take a look at it. And I have been thinking about running some variations of these through AZdecrypt but I would not know where to start. So, do you want to design such a test? I think you have the most experience with multiple rectangles. Then I’ll code it up and run it through AZdecrypt. We need to come up with some bounds though. I would prefer not to process more than 1.000.000 ciphers so that thorough settings can be used.

I could make some messages, but would prefer to wait until I understand your point of view better so that I can try to replicate what you are observing. I want to stay centered and be conservative with your time.

Personally I don’t think that Zodiac transposed an already enciphered text since this would mean that he had to draw all those symbols twice. I don’t know…but I think this guy was lazy (that’s only an assumption). The crossed out „k“ in z340 confirms that he was not willing to write the whole cipher again after he made a mistake (I would have started again since I am pedantic). Maybe he decided to make sure the symbols are not as cyclic as in z408 because z408 was broken because of the cycled symbols (repeating bigrams like double L).

I agree and was also thinking the same thing. Encoding before transposition = more work. But, he only had the opportunity to do it once, and may not have thought that at first. I have always preferred transposition before encoding, but have never been able to reconcile the strange cycle score left right top bottom.

The message is more cyclic than if transposed after encoding or if random homophonic substitution. So my thinking is that with multiple medium sized inscription rectangles, Zodiac could have still created the period 15 / 19 repeat stats, but the order of the symbols that map to medium and low frequency plaintext would not be rearranged as much as the symbols that map to high frequency plaintext.

When you are talking about schemes 1-4, what is scheme 4? In the image you posted there are only 3 schemes listed (A, B, and C)…. By the way: Do you remember my postings regarding to chunked transposition / chunk sizes? Basically a chunk based transposition is the same as a transposition with lots of very small inscription rectangles. Maybe you could check one of Jarlves test ciphers for cycles? (http://zodiackillersite.com/viewtopic.php?f=81&t=3206&p=50662&hilit=chunk#p50662)

Scheme 4 is the novelty scheme with multiple inscription rectangles. The chunk idea is what made me wonder if transposing small chunks of message could still result in high cycle scores, and it does.

If you want me to check a message, then paste it here or tell me which one you want me to check.

Thanks. It is great to have another person working on this.

Jarlve, I made a simple spreadsheet to check for unigram repeats per row.

On the third post down here, I used all perfect cycles to encode the "I like killing" message: viewtopic.php?f=81&t=3196&start=30

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
18 19 20 21 22 23 24 25 1 26 7 27 28 29 30 31 32
33 34 23 35 7 36 10 37 38 39 40 5 41 31 42 43 44
45 46 4 1 2 8 3 11 47 48 7 9 49 12 50 30 14
10 35 51 33 18 34 52 53 40 20 24 26 54 25 21 55 23
27 5 38 22 42 1 28 36 44 14 30 15 37 43 56 45 46
47 18 53 29 31 24 50 11 3 38 55 17 39 41 22 2 8
51 52 6 7 9 17 27 15 30 20 26 33 10 35 12 47 1
57 25 28 38 5 36 44 14 30 29 37 43 51 33 40 3 2
8 7 42 12 18 58 13 20 53 25 46 32 5 10 26 1 24
14 59 18 11 19 20 36 43 25 40 51 44 45 35 47 5 26
36 3 42 12 60 39 23 53 40 52 21 4 27 15 34 41 61
7 43 33 50 47 10 53 9 51 44 14 54 18 28 26 16 55
40 36 29 34 1 43 3 37 51 33 22 26 48 44 20 46 7
49 10 25 1 61 3 17 2 19 5 53 14 54 39 40 11 7
35 13 45 53 50 56 10 32 18 55 42 49 22 8 9 36 33
20 1 44 45 57 25 6 3 17 2 5 56 48 7 8 9 19
14 21 52 38 18 30 62 24 17 50 59 20 27 10 61 1 2
8 46 15 43 12 3 57 25 60 29 31 38 62 11 55 30 5
54 14 32 22 23 28 18 60 39 31 48 7 9 17 51 40 62

With perfect cycles, there are zero unigram repeats when checking by row.

And with all random homophonic symbol selection:

1 2 3 4 5 4 1 6 7 3 8 9 10 11 12 13 7
14 15 11 16 17 18 19 20 21 22 1 23 24 12 25 26 27
28 29 18 8 3 30 1 19 25 31 32 5 33 18 34 35 36
37 34 38 21 6 39 3 8 9 40 3 39 41 9 17 25 20
3 34 22 36 5 33 42 43 32 11 44 35 15 45 16 17 18
23 5 46 37 8 47 23 30 36 45 46 42 19 48 49 17 8
50 14 32 51 18 23 52 34 47 25 53 6 12 33 52 6 2
35 31 38 21 7 6 24 12 46 45 30 28 3 34 9 50 47
54 11 24 25 5 35 28 11 25 12 24 48 30 28 32 47 39
6 47 55 9 11 56 10 5 32 45 55 16 14 3 48 47 23
45 57 5 55 15 11 22 48 11 43 22 28 52 34 9 5 22
48 1 55 9 58 31 26 32 43 12 16 4 23 31 29 29 59
1 35 36 17 50 21 32 39 22 36 5 60 20 19 35 13 37
43 48 31 33 21 35 1 19 30 36 53 35 59 28 45 34 47
49 1 11 3 40 21 7 39 60 5 32 11 60 31 32 8 1
8 10 52 32 17 41 3 16 5 52 61 49 37 7 7 35 28
5 21 36 53 54 11 4 1 2 2 20 41 40 1 2 6 60
11 27 51 25 45 46 58 23 2 52 57 5 19 1 40 3 6
6 55 51 22 9 1 57 14 62 12 26 25 62 55 17 46 20
60 20 27 37 26 44 5 58 12 18 40 1 7 2 30 32 58

I found 40 unigram repeats when checking by row.

So cannot the per row measurement that you are talking about be related to some subtle disruption of the cycles?

O.k. I transposed the perfect cycle message in the post above with four 5 x 17 inscription rectangles.

1 6 11 16 21 1 29 34 10 5 44 2 48 50 51 53 54
2 7 12 17 22 26 30 23 37 41 45 8 7 30 33 40 25
3 8 13 18 23 7 31 35 38 31 46 3 9 14 18 20 21
4 9 14 19 24 27 32 7 39 42 4 11 49 10 34 24 55
5 10 15 20 25 28 33 36 40 43 1 47 12 35 52 26 23
27 1 30 45 29 3 41 52 27 33 1 5 29 40 42 20 5
5 28 15 46 31 38 22 6 15 10 57 36 37 3 12 53 10
38 36 37 47 24 55 2 7 30 35 25 44 43 2 18 25 26
22 44 43 18 50 17 8 9 20 12 28 14 51 8 58 46 1
42 14 56 53 11 39 51 17 26 47 38 30 33 7 13 32 24
14 20 51 5 12 40 15 43 53 54 55 1 33 20 25 2 54
59 36 44 26 60 52 34 33 9 18 40 43 22 46 1 19 39
18 43 45 36 39 21 41 50 51 28 36 3 26 7 61 5 40
11 25 35 3 23 4 61 47 44 26 29 37 48 49 3 53 11
19 40 47 42 53 27 7 10 14 16 34 51 44 10 17 14 7
35 56 42 36 45 17 7 21 62 20 2 12 29 55 32 60 9
13 10 49 33 57 2 8 52 24 27 8 3 31 30 22 39 17
45 32 22 20 25 5 9 38 17 10 46 57 38 5 23 31 51
53 18 8 1 6 56 19 18 50 61 15 25 62 54 28 48 40
50 55 9 44 3 48 14 30 59 1 43 60 11 14 18 7 62

And there are 30 unigram repeats when checking by rows. So I see what you mean.

I do not understand about the frequencies of unique sequence lengths peak at 17 with 26 repeats.

Here is my understanding (Jarlve, correct me if I’m wrong):

Start at the first position, then move forward in the cipher until you encounter a symbol you’ve already seen. Consider this segment of non-repeating symbols. It has length L1.

Start at the second position, then move forward in the cipher until you encounter a symbol you’ve already seen. Consider this segment of non-repeating symbols. It has length L2.

Keep doing this for the entire cipher text. Track how many segments of length 1 you found, segments of length 2 you found, segments of length 3 you found, etc.

I believe Jarlve discovered that Z340 has a peak of 26 occurrences of non-repeating segments of length 17, which is a statistically significant anomaly when compared to randomizations. And especially interesting since the row lengths happen to be 17.

Did I get this right?